Cum Să Efectuezi Analiza de Moderare în R cu un Singur Moderator

Învățarea cum să efectuezi analiza de moderare în R este esențială pentru înțelegerea relațiilor condiționate în datele tale de cercetare. Acest ghid cuprinzător îți arată cum să efectuezi analiza de moderare folosind o singură variabilă moderatoare, să interpretezi efectele de moderare, să construiești modele de moderare și să validezi asumpțiile analizei de moderare cu exemple pas cu pas și date reale.

Fie că trebuie să înțelegi cum o variabilă moderatoare schimbă relația dintre variabile, să testezi pentru efecte de moderare în modelele tale de regresie sau să înveți cum să faci analiza de moderare de la pregătirea datelor până la raportarea rezultatelor, acest tutorial acoperă tot ce ai nevoie. Vom explora analiza de moderare în R folosind pachetele lmtest, car și interactions pentru a efectua o analiză completă de moderare.

Acest ghid te învață fundamentele moderării în R, cum să interpretezi efectele de moderare, să evaluezi potrivirea modelului tău de moderare și să raportezi constatările urmând ghidurile APA. Vei stăpâni testarea asumpțiilor analizei de moderare, vizualizarea efectelor de interacțiune și înțelegerea când variabilele moderatoare influențează semnificativ rezultatele cercetării tale.

Cu toate acestea, dacă ai de-a face cu moderatori multipli, verifică ghidul nostru cuprinzător despre Cum Să Efectuezi Analizele de Moderare Multiplă în R ca un profesionist.

Ce Este Analiza de Moderare?

Analiza de moderare este o metodă analitică utilizată frecvent în cercetarea statistică pentru a examina efectele condiționate ale unei variabile independente asupra unei variabile dependente. În termeni mai simpli, evaluează cum o a treia variabilă, cunoscută sub numele de moderator, alterează relația dintre cauză (variabila independentă) și rezultat (variabila dependentă).

În limbajul statisticii, această relație poate fi descrisă folosind o ecuație de regresie multiplă moderată:

$\Large Y = \beta_{0} + \beta_{1}X + \beta_{2}Z + \beta_{3}XZ + \epsilon$

Unde:

Y reprezintă variabila dependentă
X este variabila independentă
Z simbolizează variabila moderatoare
β0, β1, β2 și β3 denotă coeficienții reprezentând interceptul, efectul variabilei independente, efectul moderatorului și efectul de interacțiune dintre variabila independentă și moderator respectiv
ε reprezintă termenul de eroare

În analiza de moderare, componenta cheie este termenul de interacțiune (β3*XZ). Dacă coeficientul β3 este semnificativ statistic (valoarea p <0,05), indică prezența unui efect de moderare.

Valoarea analizei de moderare constă în capacitatea sa de a dezvălui relații condiționate. În loc să întrebăm "X afectează Y?", întrebăm "Relația X→Y depinde de Z?" Acest lucru ne ajută să înțelegem în ce condiții sau pentru cine apar efectele.

Asumpții ale Analizei de Moderare

Trebuie îndeplinite mai multe asumpții când efectuezi analiza de moderare. Aceste asumpții sunt similare cu cele pentru regresia liniară multiplă, dat fiind că analiza de moderare implică de obicei regresie multiplă unde este inclus un termen de interacțiune. Iată asumpțiile principale:

Linearitate: Relația dintre fiecare predictor (variabila independentă și moderator) și rezultat (variabila dependentă) este liniară. Această asumpție poate fi verificată vizual folosind grafice de dispersie pe care le vom genera și explica în detaliu în acest articol.
Independența observațiilor: Se presupune că observațiile sunt independente una de alta. Aceasta este mai mult o problemă de design al studiului decât ceva ce poate fi testat. Dacă datele tale sunt serii temporale sau grupate, această asumpție este probabil violată.
Homoscedasticitate: Aceasta se referă la asumpția că varianța erorilor este constantă pe toate nivelurile variabilelor independente. Cu alte cuvinte, răspândirea reziduurilor ar trebui să fie aproximativ aceeași pe toate valorile prezise. Acest lucru poate fi verificat prin examinarea unui grafic al reziduurilor față de valorile prezise.
Normalitatea reziduurilor: Se presupune că reziduurile (erorile) urmează o distribuție normală. Acest lucru poate fi verificat folosind un grafic Q-Q.
Absența multicolinearității: Variabila independentă și moderatorul nu ar trebui să fie puternic corelați. Corelația ridicată (multicolinearitate) poate infla varianța coeficienților de regresie și poate face estimările foarte sensibile la schimbări minore în model. Factorul de inflație a varianței (VIF) este adesea folosit pentru a verifica multicolinearitatea.
Absența cazurilor influente: Analiza nu ar trebui să fie influențată excesiv de nicio observație singulară. Distanța Cook poate fi folosită pentru a verifica cazurile influente care ar putea influența nejustificat estimarea coeficienților de regresie.

Formularea Modelului de Analiză de Moderare

Să presupunem că căutăm răspunsul la următoarea întrebare de cercetare:

"Cum variază relația dintre consumul de cafea (măsurat prin numărul de cești consumate) și productivitatea angajaților în funcție de toleranța individuală la cofeină?"

Prin urmare, putem formula următoarea ipoteză:

"Nivelul toleranței individuale la cofeină moderează relația dintre consumul de cafea și productivitate."

Ceea ce încercăm în esență să răspundem cu această ipoteză este dacă impactul consumului de cafea asupra productivității este același pentru toți indivizii sau dacă se schimbă pe baza toleranței lor la cofeină. Cu alte cuvinte, investigăm dacă beneficiile (sau dezavantajele) de productivitate ale cafelei sunt aceleași pentru toată lumea sau dacă diferă în funcție de cât de tolerantă este o persoană la cofeină.

Prin urmare, studiul nostru constă din următoarele variabile: consumul de cafea (variabila independentă), productivitatea (variabila dependentă) și toleranța la cofeină (moderatorul).

Următoarea diagramă explică tipul de variabile din studiul nostru și relația dintre ele în contextul analizei de moderare:

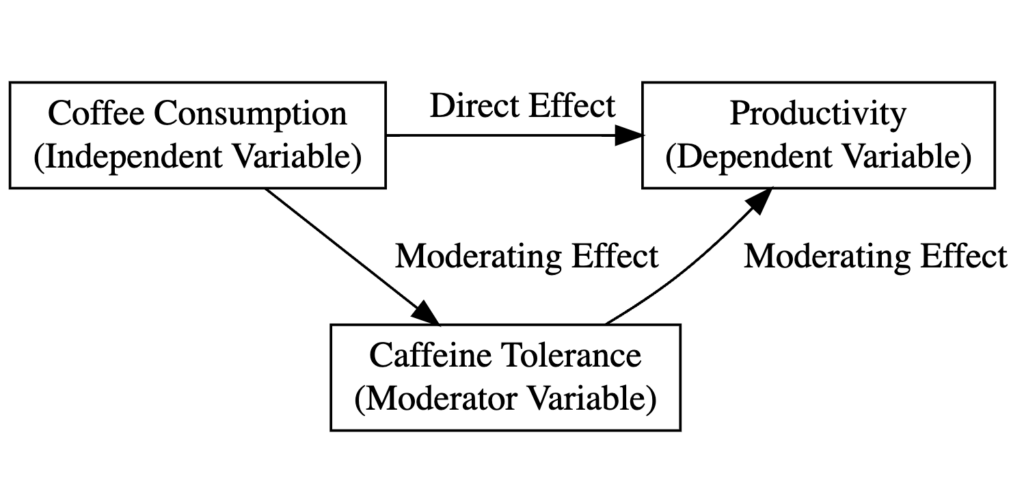
Diagramă de analiză de moderare arătând consumul de cafea ca variabilă independentă, productivitatea ca variabilă dependentă și toleranța la cofeină ca variabilă moderatoare cu căi de efect direct și moderator

Diagramă model de analiză de moderare ilustrând relația dintre consumul de cafea (X), productivitatea (Y) și toleranța la cofeină (moderator).

Unde:

Consumul de cafea (Cești) este variabila independentă.
Productivitatea angajaților (Productivitate) este variabila dependentă.
Toleranța individuală la cofeină (Toleranță) este variabila moderatoare.
Efectul direct arată cum consumul de cafea impactează productivitatea în general.
Efectul moderator (interacțiune) arată dacă această relație diferă pe baza nivelurilor de toleranță la cofeină. Dacă este semnificativ, înseamnă că relația cafea-productivitate este mai puternică (sau mai slabă) pentru persoanele cu toleranță ridicată vs. scăzută la cofeină.

Cum Să Efectuezi Analiza de Moderare în R

Acum că am acoperit suficient teren teoretic, este timpul să ne ocupăm cu învățarea cum să efectuăm analiza de moderare în R. Sperăm că ai deja R/R Studio instalat și funcțional, dar dacă nu, iată un ghid rapid despre cum să instalezi R și R Studio pe computerul tău.

Vom rămâne la exemplul "cafelei" menționat anterior pentru această lecție. Amintește-ți, am ipotezat că nivelul toleranței individuale la cofeină moderează relația dintre consumul de cafea și productivitate.

Pasul 1: Instalarea și Încărcarea Pachetelor Necesare în R

R oferă multe pachete care ajută la analiza de moderare. În cazul nostru, vom folosi patru pachete, respectiv: lmtest, car, interactions și ggplots2. Iată o descriere a fiecărui pachet și scopul său:

lmtest: Pachetul lmtest oferă instrumente pentru verificarea diagnostică în modelele de regresie liniară, care sunt esențiale pentru a ne asigura că modelul nostru satisface asumpțiile cheie. Acest pachet poate efectua testele Wald, F și raportul de verosimilitate. În contextul analizei de moderare, ai putea folosi lmtest pentru a verifica heteroscedasticitatea (varianța neconstantă a erorilor) printre alte lucruri.
car: Pachetul car (Companion to Applied Regression) este un alt instrument pentru diagnosticarea regresiei și include funcții pentru calculele factorului de inflație a varianței (VIF), care pot ajuta la detectarea problemelor de multicolinearitate (când variabilele independente sunt puternic corelate între ele). Multicolinearitatea poate cauza probleme în estimarea coeficienților de regresie și a erorilor lor standard.
interactions: Pachetul interactions este folosit pentru a crea vizualizări și analize de pantă simplă ale termenilor de interacțiune în modelele de regresie. Poate produce diverse tipuri de grafice pentru a ajuta la vizualizarea efectului de moderare și cum se schimbă relația dintre variabila independentă și variabila dependentă la diferite niveluri ale moderatorului.
ggplot2: ggplot2 este unul dintre cele mai populare pachete pentru vizualizarea datelor în R. În analiza de moderare, ggplot2 poate fi folosit pentru a crea grafice de dispersie, grafice lineare și alte vizualizări pentru a te ajuta să înțelegi mai bine datele noastre și relațiile dintre variabile. În plus, poate ajuta la vizualizarea efectului de moderare, adică cum se schimbă efectul unei variabile independente asupra unei variabile dependente pe nivelurile variabilei moderatoare.

Putem instala pachetele enumerate mai sus dintr-o dată copiind și lipind următoarea comandă în consola R:

install.packages("lmtest")
install.packages("car")
install.packages("interactions")
install.packages("ggplot2")

Odată instalate, încarcă pachetele în sesiunea R:

library(lmtest)
library(car)
library(interactions)
library(ggplot2)

Pasul 2: Importarea Datelor

Pentru a-ți face mai ușor să înveți cum să efectuezi analiza de moderare în R, poți descărca setul de date de practică din bara laterală - un set de date dummy de 30 de respondenți conținând scoruri pentru variabilele din studiul nostru: consumul de cafea (Cești), toleranța la cofeină (Toleranță) și productivitatea (Productivitate).

Învață cum să imporți fișiere Excel .xls sau .xlsx în R
Învață cum să imporți un fișier CSV în R

Dacă setul tău de date nu este prea mare, poți insera datele manual în R sub formă de data frame după cum urmează:

data <- data.frame(
 Respondent = 1:30,
 Cups = c(2, 4, 1, 3, 2, 3, 1, 2, 2, 4, 2, 3, 1, 3, 3, 2, 2, 4, 1, 3, 2, 3, 1, 2, 2, 4, 2, 3, 1, 3),
 Tolerance = c(7, 5, 6, 7, 8, 6, 7, 7, 6, 8, 7, 7, 6, 7, 8, 6, 7, 5, 6, 7, 8, 6, 7, 7, 6, 8, 7, 7, 6, 7),
 Productivity = c(5, 6, 4, 6, 7, 7, 4, 6, 5, 7, 5, 6, 4, 6, 7, 5, 5, 6, 4, 6, 7, 7, 4, 6, 5, 7, 5, 6, 4, 6)
)

IMPORTANT: Acest set de date poate fi folosit doar în scopuri educaționale deoarece conține valori aleatorii și s-ar putea să nu reflecte un scenariu din lumea reală. "Cups" (variabila independentă) reflectă numărul de cești de cafea consumate pe zi, "Tolerance" (variabila moderatoare) este un scor din 10 care reflectă cât de bine tolerează individul cofeina și "Productivity" (variabila dependentă) este un scor din 10 indicând nivelul de productivitate al individului.

Pasul 3: Adaptarea Modelului de Regresie Multiplă Moderată

Pentru a adapta un model de regresie multiplă moderată, vom folosi funcția lm() în R. Reține că data este data frame-ul nostru și Cups, Tolerance și Productivity sunt coloane în acel data frame.

model <- lm(Productivity ~ Cups*Tolerance, data)
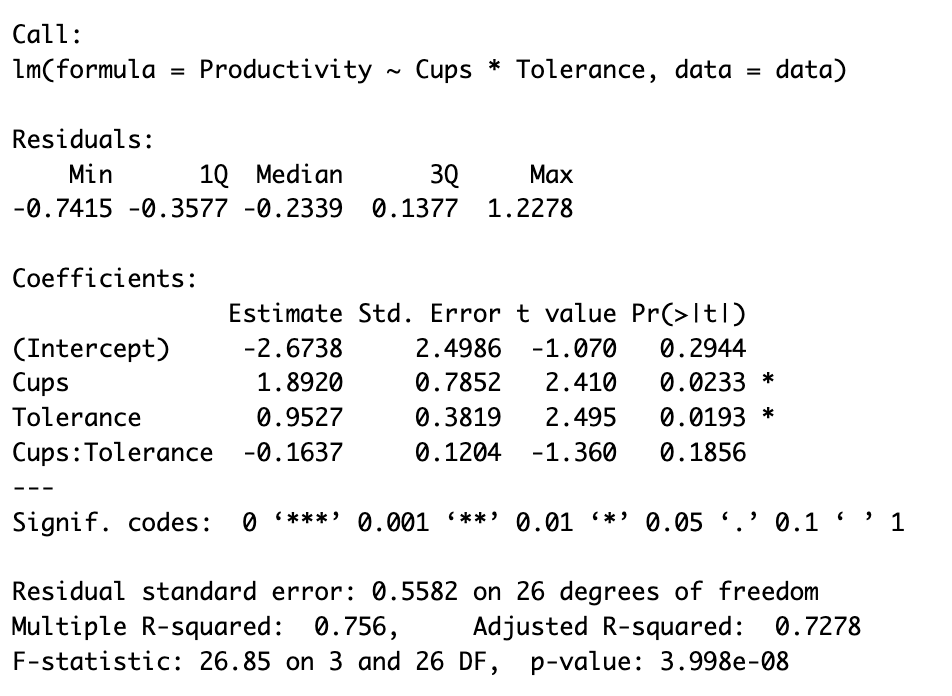
summary(model)

Această comandă va afișa rezumatul modelului incluzând o analiză detaliată a potrivirii modelului și semnificația fiecărui termen în model așa cum vedem în captura de mai jos:

Ieșire consolă R arătând statistici rezumat lm() pentru analiza de moderare incluzând coeficienți, valori R-pătrat, statistica F și rezultate ale termenului de interacțiune

Ieșire R arătând rezultatele regresiei multiple moderate cu coeficientul termenului de interacțiune (Cups:Tolerance) și nivelurile de semnificație.

Pasul 4: Interpretarea Efectului de Moderare

Ieșirea lm() oferă informațiile cheie pentru interpretarea moderării. Concentrează-te pe acești coeficienți:

Cups: Efect pozitiv (1,8920, p < 0,05) - consumul de cafea crește productivitatea
Tolerance: Efect pozitiv (0,9527, p < 0,05) - toleranța mai mare la cofeină crește productivitatea
Cups:Tolerance: Termenul de interacțiune (-0,1637, p > 0,05) - nu este semnificativ statistic

Deoarece valoarea p a interacțiunii depășește 0,05, concluzionăm că nu există efect semnificativ de moderare. Relația dintre cafea și productivitate nu depinde în mod semnificativ de toleranța la cofeină în acest eșantion.

Performanța Modelului:

R² = 0,756: Modelul explică 75,6% din varianța productivității
R² Ajustat = 0,728: Rămâne ridicat după ajustarea pentru predictori
Statistica F (p < 0,001): Modelul general este semnificativ statistic

Pasul 5: Vizualizarea Efectului de Interacțiune

Putem genera cu ușurință un grafic pentru a ne ajuta să vizualizăm efectul de interacțiune folosind funcția interact_plot în R folosind următorul cod:

interactions::interact_plot(model, pred = Cups, modx = Tolerance)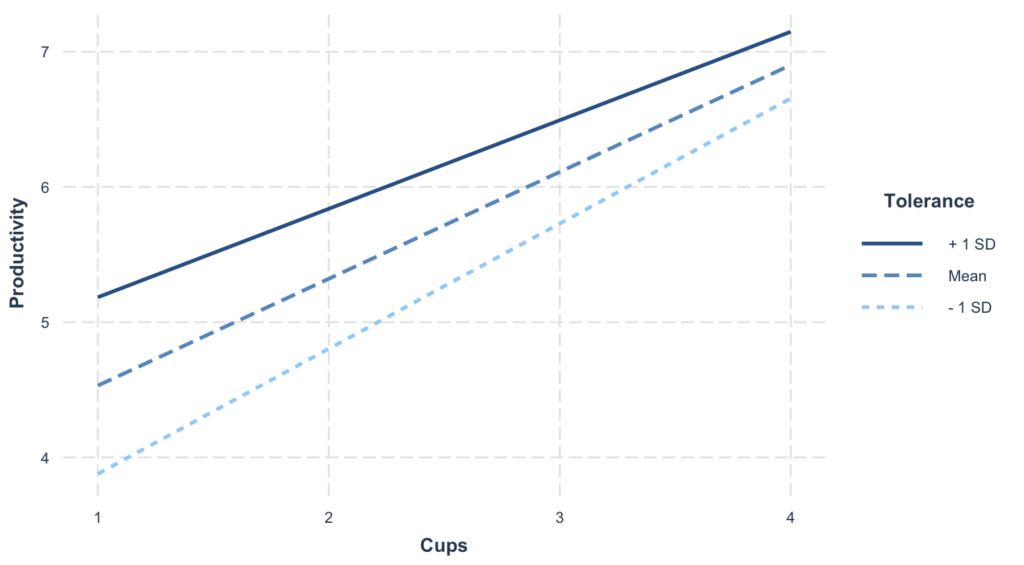

Grafic de interacțiune arătând trei linii reprezentând diferite niveluri de toleranță la cofeină și cum consumul de cafea afectează productivitatea la fiecare nivel de toleranță

Grafic de interacțiune vizualizând efectul moderator al toleranței la cofeină asupra relației dintre consumul de cafea și productivitate.

Acest grafic arată cum se schimbă relația cafea-productivitate la diferite niveluri de toleranță. Fiecare linie reprezintă un nivel diferit al moderatorului (toleranță scăzută, medie, ridicată).

Interpretare cheie:

Linii non-paralele = Există moderare (efectul cafelei depinde de toleranță)
Linii paralele = Nu există moderare (efectul cafelei este același indiferent de toleranță)
Benzile de încredere arată incertitudinea în jurul fiecărei pante

Pasul 6: Evaluarea Asumpțiilor și Diagnosticelor Modelului

Înainte de a avea încredere în rezultatele noastre, trebuie să verificăm asumpțiile regresiei: linearitate, independență, homoscedasticitate, normalitate și absența multicolinearității. De asemenea, vom verifica valorile extreme și observațiile influente care ar putea distorsiona constatările noastre.

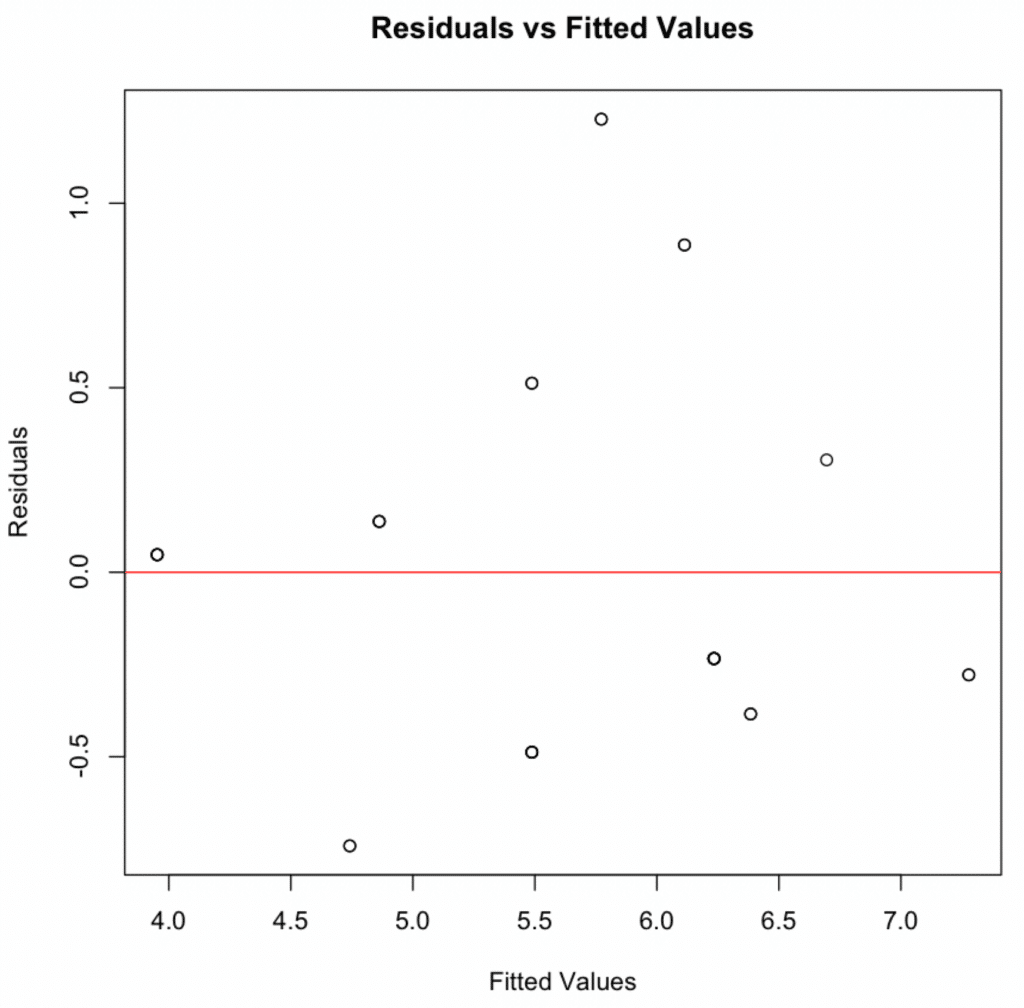
1. Linearitate și Aditivitate

Reprezintă grafic reziduurile față de valorile adaptate. Împrăștierea aleatoare în jurul valorii zero indică că linearitatea este îndeplinită.

Grafic diagnostic reziduuri vs valori adaptate arătând puncte împrăștiate aleatoriu în jurul liniei orizontale zero testând asumpția de linearitate în analiza de moderare

Grafic reziduuri vs valori adaptate demonstrând că asumpția de linearitate este îndeplinită cu model de împrăștiere aleatorie.

2. Independența Reziduurilor

Testul Durbin-Watson detectează autocorelarea în reziduuri:

print(dwtest(model))

Durbin-Watson = 1,9833 (aproape de 2), valoare p = 0,5468 → Nu există autocorelare. Asumpția de independență este îndeplinită.

Ieșire consolă R afișând rezultatele testului Durbin-Watson cu statistica DW de 1,9833 și valoarea p de 0,5468 indicând absența autocorelării

Ieșire test Durbin-Watson arătând DW = 1,9833, confirmând asumpția independenței reziduurilor.

3. Homoscedasticitate

Verifică varianța egală a reziduurilor pe valorile adaptate:

Grafic Scale-Location arătând rădăcina pătrată a reziduurilor standardizate față de valorile adaptate testând asumpția de homoscedasticitate cu linie roșie relativ plată

Grafic diagnostic Scale-Location demonstrând homoscedasticitatea cu varianță constantă pe valorile adaptate.

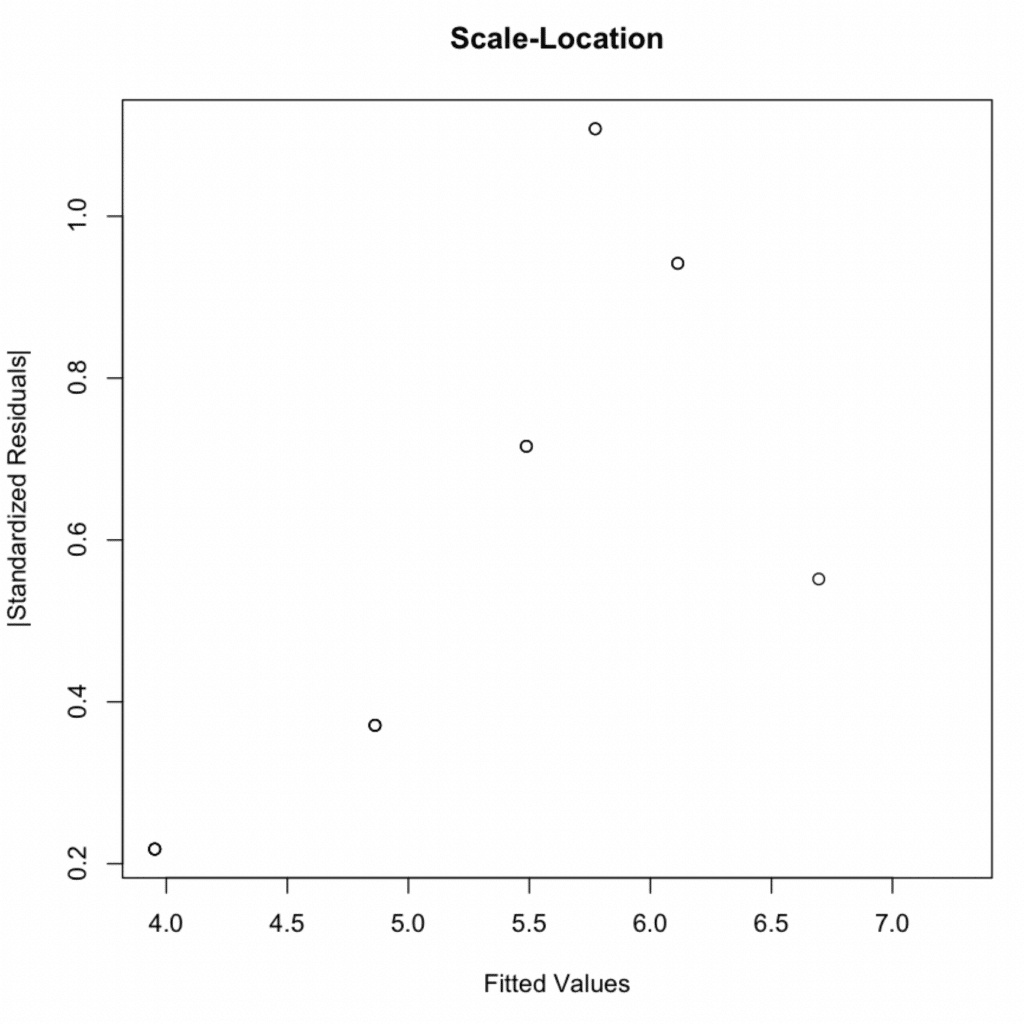
Confirmă cu testul Breusch-Pagan:

print(bptest(model))

Consolă R arătând rezultatele testului Breusch-Pagan cu statistica BP de 4,1203 și valoarea p de 0,2488 confirmând homoscedasticitatea

Ieșire test Breusch-Pagan cu valoare p = 0,2488, confirmând că asumpția de varianță egală este îndeplinită.

Valoare p = 0,2488 > 0,05 → Asumpția de homoscedasticitate este îndeplinită.

4. Normalitatea Reziduurilor

Folosește un grafic Q-Q pentru a verifica dacă reziduurile urmează o distribuție normală. Punctele ar trebui să se afle de-a lungul liniei diagonale.

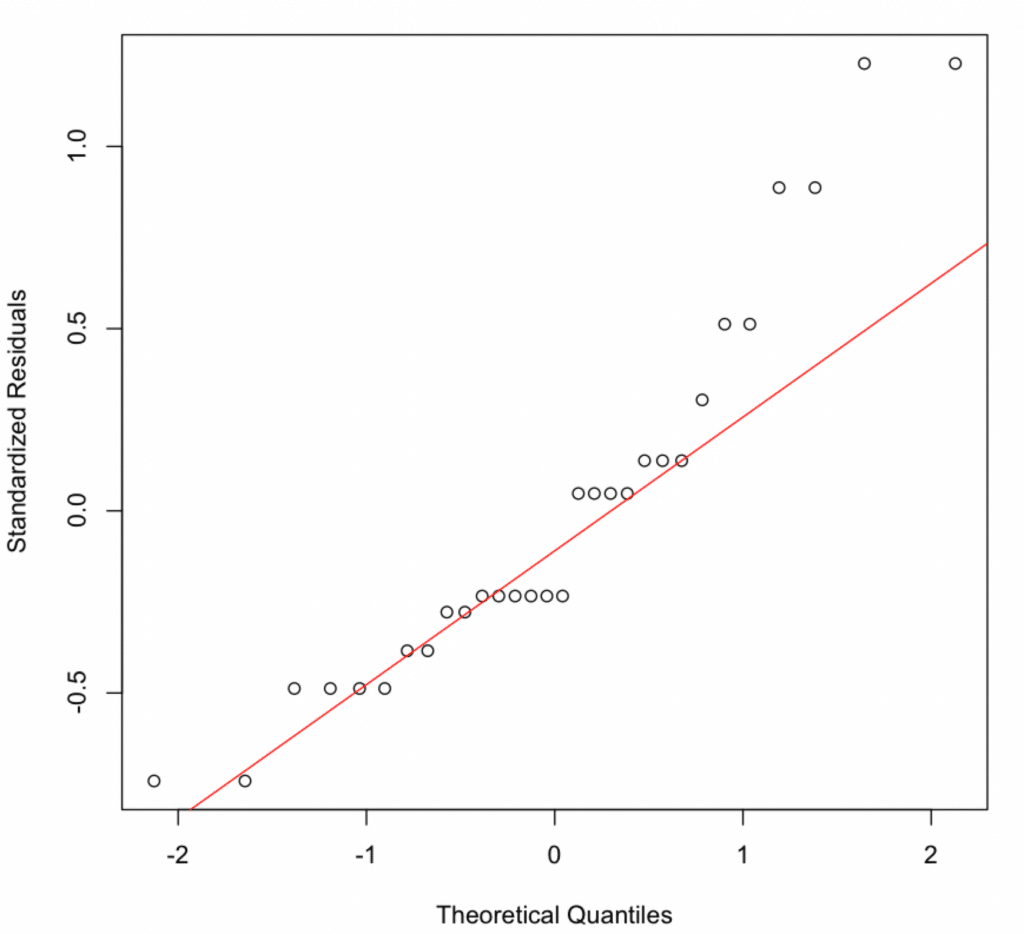
Grafic Q-Q arătând cuantilele teoretice vs reziduurile standardizate cu puncte urmând parțial linia diagonală testând asumpția de normalitate

Grafic Normal Q-Q arătând reziduuri urmând parțial linia diagonală cu abateri ușoare la cozi.

Graficul Q-Q arată abateri ușoare. Confirmă cu testul Shapiro-Wilk:

shapiro.test(resid(model))

Consolă R afișând rezultatele testului de normalitate Shapiro-Wilk cu statistica W de 0,91229 și valoarea p de 0,008773 pentru reziduuri

Ieșire test Shapiro-Wilk arătând valoare p = 0,0088, indicând abatere ușoară de la normalitatea perfectă.

Valoare p = 0,0088 < 0,05 indică faptul că reziduurile nu sunt distribuite perfect normal. Cu toate acestea, cu eșantioane mici (n=30), acest test este foarte sensibil la abateri minore. Graficul Q-Q arată doar abateri ușoare, iar regresia este robustă la violări moderate ale normalității datorită Teoremei Limitei Centrale.

5. Multicolinearitate

Verifică multicolinearitatea folosind factorul de inflație a varianței (VIF). VIF > 10 indică multicolinearitate ridicată.

print(vif(model))

Consolă R arătând valorile factorului de inflație a varianței VIF cu Cups la 53,36, Tolerance la 9,30 și termenul de interacțiune la 65,12 indicând multicolinearitate așteptată

Ieșire VIF arătând multicolinearitate ridicată așteptată datorită termenului de interacțiune în analiza de moderare.

Valorile VIF: Cups = 53,36, Tolerance = 9,30, Cups:Tolerance = 65,12. Aceste valori ridicate sunt așteptate și acceptabile în analiza de moderare. Termenii de interacțiune sunt prin definiție corelați cu variabilele lor componente. Pentru a reduce VIF, centrează variabilele înainte de a crea termenul de interacțiune (scade media din fiecare valoare).

6. Valori Extreme și Observații Influente

Detectează valorile extreme folosind testul Bonferroni pentru valori extreme:

print(outlierTest(model))

Consolă R arătând rezultatele testului Bonferroni pentru valori extreme cu cel mai mare reziduu studentizat de 2,516731 la observația 6 și valoarea p Bonferroni de 0,55887

Ieșire test Bonferroni pentru valori extreme indicând absența valorilor extreme semnificative statistic după corecția pentru testare multiplă.

Observația 6 are cel mai mare reziduu (2,517), dar valoarea p Bonferroni = 0,559 > 0,05 → Nu au fost detectate valori extreme semnificative.

Verifică observațiile influente folosind distanța Cook:

# Observații influente
influence <- influence.measures(model)
 
# Afișează valorile distanței Cook pentru fiecare observație
print(influence$is.inf)
 
# Reprezintă grafic distanța Cook
plot(influence$infmat[, "cook.d"],
 main = "Grafic distanță Cook",
 ylab = "Distanță Cook",
 ylim = c(0, max(1, max(influence$infmat[, "cook.d"]))))
 
# Adaugă o linie de referință pentru distanța Cook = 1
abline(h = 1, col = "red")

Valorile distanței Cook peste 1 indică observații foarte influente.

Valori distanță Cook arătând absența observațiilor influente în analiza de moderare în R

Măsuri de influență distanță Cook pentru analiza de moderare în R.

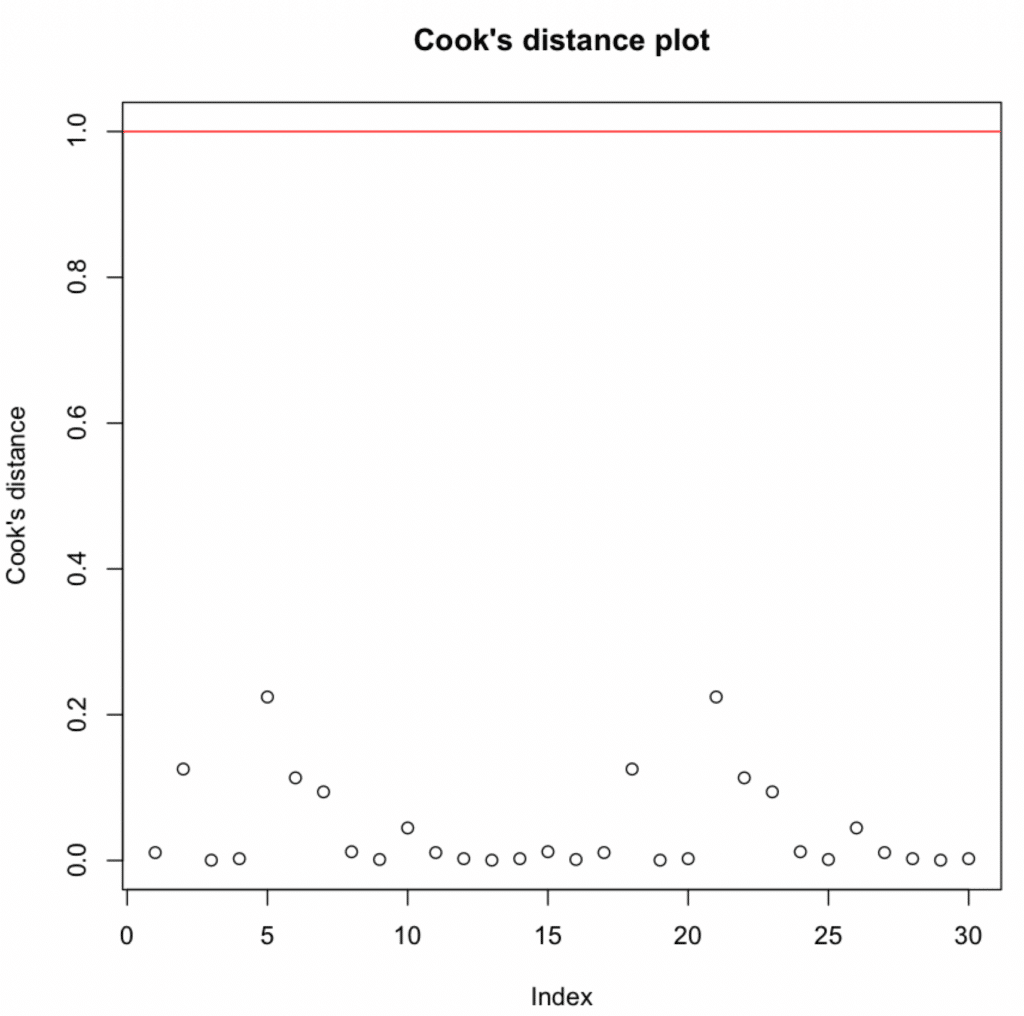
Grafic distanță Cook pentru analiza de moderare în R arătând absența punctelor influente

Grafic distanță Cook arătând toate observațiile sub pragul de 1.

Toate valorile sunt sub 1 → Nu au fost detectate observații influente.

Exportă graficele diagnostice în PDF:

# Adaptează modelul
model <- lm(Productivity ~ Cups*Tolerance, data = data)
 
# Grafice Diagnostice
par(mfrow = c(2, 2), oma = c(0, 0, 2, 0))
plot(model, las = 1)
mtext("Grafice Diagnostice", outer = TRUE, line = -1, cex = 1.5)
 
# Salvează graficele ca fișier PDF
pdf("Diagnostic_Plots.pdf")
par(mfrow = c(2, 2), oma = c(0, 0, 2, 0))
plot(model, las = 1)
mtext("Grafice Diagnostice", outer = TRUE, line = -1, cex = 1.5)
dev.off()

Scriptul de mai sus adaptează modelul, creează patru grafice diagnostice relevante și apoi salvează aceste grafice ca fișier PDF numit "Diagnostic_Plots.pdf". Aceste grafice diagnostice ne ajută să verificăm asumpțiile de linearitate, independență, homoscedasticitate și absența observațiilor influente, respectiv.

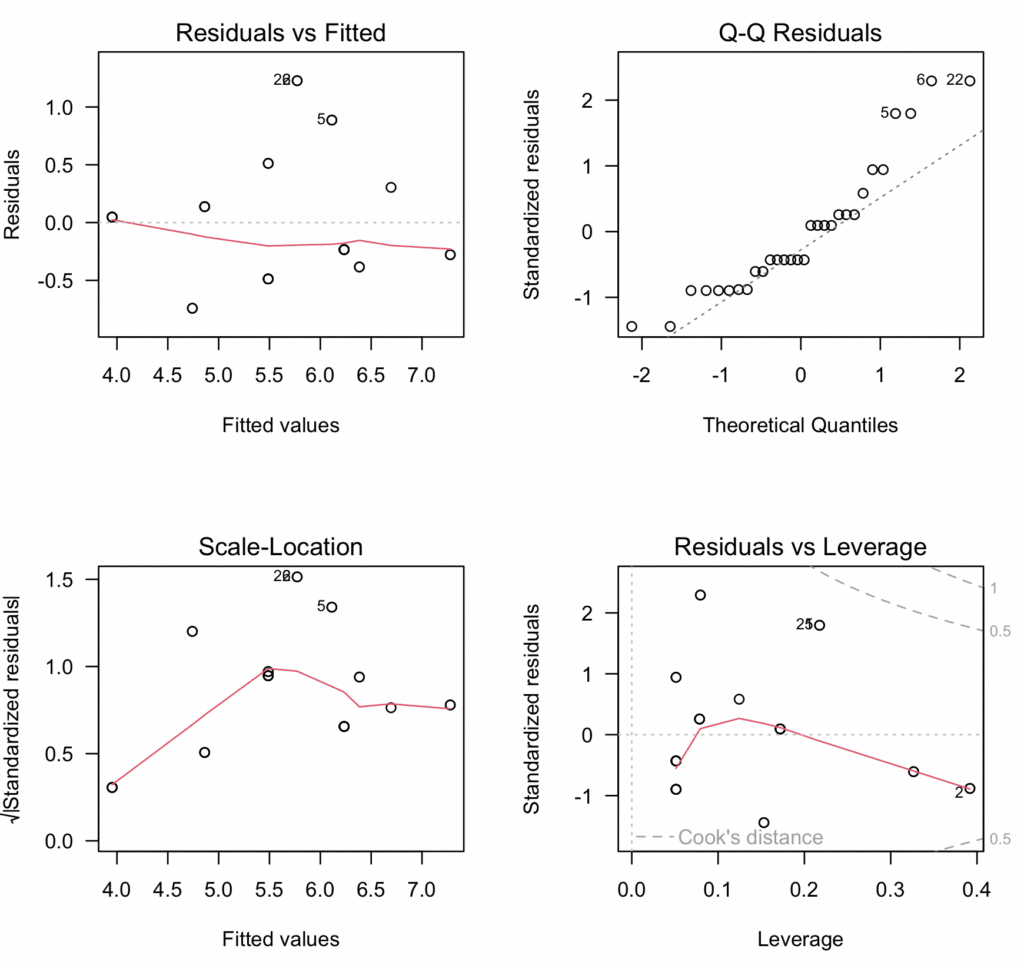
Grafic diagnostic cu patru panouri arătând reziduuri vs adaptate, grafic Q-Q, grafic scale-location și reziduuri vs leverage pentru testarea cuprinzătoare a asumpțiilor analizei de moderare

Grafic diagnostic cuprinzător cu patru panouri pentru analiza de moderare arătând toate testele de asumpții într-o singură vizualizare.

Pasul 7: Raportarea Rezultatelor

În final, este timpul să rezumăm constatările noastre și să raportăm rezultatele analizei de moderare de mai sus pe care am efectuat-o în R după cum urmează:

În analiza noastră de moderare în R, am urmărit să investigăm efectul consumului de cofeină (măsurat prin numărul de cești de cafea consumate) și toleranța la stres asupra productivității, luând în considerare și potențialul efect moderator al toleranței la stres asupra relației dintre consumul de cofeină și productivitate. Aceasta a fost realizată printr-un model de regresie multiplă, specificat cu un termen de interacțiune pentru ceștile de cafea și toleranța la stres.

Modelul adaptat a oferit perspective valoroase asupra relațiilor ipotezate. Termenul de interacțiune (Cups*Tolerance) nu a fost semnificativ statistic (p > 0,05), sugerând absența unui efect semnificativ de moderare al toleranței la cofeină asupra relației dintre consumul de cafea și productivitate în acest eșantion. Aceasta implică faptul că efectul cafelei asupra productivității nu diferă semnificativ pe baza nivelului de toleranță la cofeină al unui individ, cel puțin nu în acest set de date.

Analiza ulterioară a asumpțiilor și diagnosticelor modelului a dezvăluit că modelul este o potrivire adecvată pentru datele noastre:

Linearitate și Aditivitate: Graficul reziduuri vs valori adaptate a indicat că relația era liniară și aditivă, fără modele sau abateri discernibile de la media zero.
Independența Reziduurilor: Testul Durbin-Watson a rezultat într-o statistică de 1,9833 (valoare p = 0,5468), indicând absența dovezilor de autocorelare în reziduuri.
Homoscedasticitate: Graficul scale-location și testul Breusch-Pagan (valoare p = 0,2488) au confirmat asumpția de varianță egală (homoscedasticitate) a reziduurilor.
Normalitatea reziduurilor: Testul Shapiro-Wilk a indicat că reziduurile nu au urmat o distribuție perfect normală (valoare p = 0,0088 < 0,05). Cu toate acestea, având în vedere dimensiunea mică a eșantionului (n=30), acest test este foarte sensibil la abateri minore, iar graficul vizual Q-Q a arătat doar abateri ușoare de la normalitate. Cu eșantioane mai mari, modelele de regresie sunt robuste la violări moderate ale normalității datorită Teoremei Limitei Centrale.
Multicolinearitate: Factorii de inflație a varianței (VIF) pentru predictori au fost peste pragul tipic de 5, indicând prezența multicolinearității. Cu toate acestea, având în vedere că acest lucru era așteptat datorită includerii termenilor de interacțiune, aceasta nu invalidează modelul nostru.
Valori extreme și observații influente: Testul Bonferroni pentru valori extreme nu a detectat valori extreme semnificative. Valorile distanței Cook au fost toate sub pragul de 1, sugerând absența punctelor influente excesiv.

În concluzie, analiza noastră de moderare în R nu a găsit un efect semnificativ statistic de moderare al toleranței la cofeină asupra relației dintre consumul de cafea și productivitate. Deși modelul a explicat o proporție substanțială a varianței (R² = 0,756), termenul de interacțiune nu a fost semnificativ. Acest lucru sugerează că, în acest eșantion, efectul cafelei asupra productivității nu variază semnificativ pe baza nivelurilor de toleranță la cofeină. Aceste constatări evidențiază importanța unei dimensiuni adecvate a eșantionului și nevoia de studii de replicare pentru a detecta în mod fiabil efectele de moderare.

IMPORTANT: Te rog reține să ajustezi interpretarea la rezultatele și contextul tău real. Acesta este un exemplu generic și s-ar putea să nu se alinieze complet cu obiectivele și rezultatele tale specifice de cercetare.

Întrebări Frecvente

Cum efectuez analiza de moderare în R?

Pentru a efectua analiza de moderare în R: (1) Instalează pachetele necesare (lmtest, car, interactions, ggplot2), (2) Încarcă datele cu variabila independentă, moderator și variabila dependentă, (3) Creează termenul de interacțiune folosind sintaxa X*Z, (4) Adaptează modelul cu lm(Y ~ X*Z, data), (5) Verifică ieșirea rezumatului pentru semnificația efectului de interacțiune, (6) Vizualizează cu interact_plot(), (7) Testează asumpțiile. Termenul de interacțiune (X:Z) indică dacă este prezentă moderarea.

Ce este o variabilă moderatoare în statistică?

O variabilă moderatoare (sau moderator) este o a treia variabilă care afectează puterea sau direcția relației dintre o variabilă independentă și o variabilă dependentă. De exemplu, dacă studiezi efectul consumului de cafea asupra productivității, toleranța la cofeină ar putea fi o variabilă moderatoare - efectul cafelei ar putea fi mai puternic pentru persoanele cu toleranță ridicată față de toleranță scăzută.

Care sunt asumpțiile analizei de moderare?

Asumpțiile analizei de moderare includ: (1) Linearitate - relație liniară între predictori și rezultat, (2) Independența observațiilor - fără autocorelare, (3) Homoscedasticitate - varianță constantă a reziduurilor, (4) Normalitatea reziduurilor - erorile sunt distribuite normal, (5) Absența multicolinearității - variabila independentă și moderatorul nu sunt puternic corelați (VIF < 10), (6) Absența cazurilor influente - nicio observație singulară nu influențează nejustificat rezultatele (distanța Cook < 1).

Cum interpretez un efect moderator?

Pentru a interpreta un efect moderator: Uită-te la termenul de interacțiune (X:Z) în ieșirea ta de regresie. Dacă valoarea p este < 0,05, există moderare - înseamnă că efectul lui X asupra lui Y se schimbă în funcție de nivelurile lui Z. Un coeficient pozitiv înseamnă că efectul se întărește pe măsură ce Z crește; negativ înseamnă că se slăbește. Folosește grafice de interacțiune pentru a vizualiza cum se schimbă relația X-Y la diferite niveluri ale moderatorului.

Care este diferența dintre moderare și mediere?

Moderarea examinează CÂND sau PENTRU CINE apare un efect (moderatorul schimbă puterea/direcția relației X→Y), în timp ce medierea examinează CUM sau DE CE apare un efect (mediatorul explică mecanismul prin care X afectează Y). Moderarea implică efecte de interacțiune (X*Z), în timp ce medierea implică efecte indirecte (calea X→M→Y). Ambele răspund la întrebări diferite de cercetare despre relațiile dintre variabile.

Cum testez asumpțiile analizei de moderare în R?

Testează asumpțiile de moderare în R folosind: (1) Linearitate: plot(model) reziduuri vs adaptate, (2) Independență: dwtest(model) pentru testul Durbin-Watson, (3) Homoscedasticitate: bptest(model) pentru testul Breusch-Pagan, (4) Normalitate: shapiro.test(resid(model)) și grafice Q-Q, (5) Multicolinearitate: vif(model) unde valorile > 10 indică probleme, (6) Cazuri influente: outlierTest(model) și grafice distanță Cook. VIF ridicat este așteptat cu termeni de interacțiune.

Cum raportez rezultatele analizei de moderare?

Raportează rezultatele de moderare prin afirmarea: (1) Coeficientul termenului de interacțiune și semnificația (de ex., β = -0,16, p > 0,05), (2) Dacă a fost găsită moderarea (interacțiune semnificativă = da), (3) Statistici de potrivire a modelului (R², statistica F, valoarea p), (4) Pante simple la diferite niveluri ale moderatorului dacă este semnificativ, (5) Toate rezultatele testelor de asumpții (Durbin-Watson, Breusch-Pagan, valori VIF), (6) Include grafic de interacțiune, (7) Interpretează semnificația practică în contextul întrebării tale de cercetare.

Ce înseamnă un termen de interacțiune semnificativ în analiza de moderare?

Un termen de interacțiune semnificativ (p < 0,05) înseamnă că există moderare - efectul variabilei tale independente asupra variabilei dependente depinde de nivelul moderatorului. De exemplu, dacă X:Z este semnificativ, înseamnă că Z moderează relația X→Y. Relația dintre X și Y este diferită la niveluri scăzute vs. ridicate ale lui Z. Aceasta este vizualizată ca linii non-paralele într-un grafic de interacțiune.

Cum vizualizez efectele de moderare în R?

Vizualizează moderarea în R folosind interact_plot() din pachetul interactions: interact_plot(model, pred = VariabilaIndependentă, modx = Moderator). Aceasta creează un grafic arătând cum se schimbă relația dintre predictorul tău și rezultat la diferite niveluri ale moderatorului (de obicei media, +1 SD, -1 SD). Liniile non-paralele indică moderare; liniile paralele sugerează absența efectului de moderare.

Ce este un model de moderare?

Un model de moderare este un model statistic care testează dacă o a treia variabilă (moderator) influențează puterea sau direcția relației dintre o variabilă independentă și una dependentă. Ecuația modelului este: Y = β₀ + β₁X + β₂Z + β₃XZ + ε. Termenul de interacțiune (β₃XZ) este esențial - dacă este semnificativ, indică moderare. Aceasta testează efecte condiționate mai degrabă decât efecte directe.

De ce este VIF-ul meu ridicat în analiza de moderare?

Valorile VIF (Factorul de Inflație a Varianței) ridicate în analiza de moderare sunt așteptate și normale când incluzi termeni de interacțiune. Termenul de interacțiune (X*Z) este matematic corelat cu variabilele sale componente (X și Z) prin definiție. VIF > 10 pentru efectele principale este de obicei acceptabil în modelele de moderare. Pentru a reduce preocupările legate de multicolinearitate, poți centra variabilele tale pe medie înainte de a crea termenul de interacțiune, ceea ce adesea scade valorile VIF.

Cum interpretez variabilele moderatoare?

Interpretează variabilele moderatoare examinând: (1) Este interacțiunea semnificativă? Dacă da, există moderare, (2) Care este direcția coeficientului? Pozitiv = efect de întărire, negativ = efect de slăbire, (3) Reprezintă grafic pantele simple la diferite niveluri ale moderatorului (scăzut, mediu, ridicat) pentru a vedea cum se schimbă relația X-Y, (4) Raportează dimensiunile efectului la valori specifice ale moderatorului, (5) Discută implicațiile practice - pentru cine sau în ce condiții X afectează cel mai puternic Y?

Concluzie

În acest ghid cuprinzător, ai învățat cum să efectuezi analiza de moderare în R de la început până la sfârșit. Acum înțelegi ce sunt variabilele moderatoare, cum să testezi pentru efecte moderatoare, să construiești și să evaluezi modele de moderare și să validezi toate asumpțiile analizei de moderare folosind teste diagnostice și vizualizări.

Ai stăpânit abilitățile esențiale pentru moderare în R: crearea termenilor de interacțiune, interpretarea efectelor de moderare, folosirea funcției lm() pentru analiza moderatorului și vizualizarea rezultatelor cu grafice de interacțiune. Fie că investighezi variabile moderatoare în cercetarea psihologică, analiza de afaceri sau științele sociale, acum poți efectua cu încredere analiza de moderare completă și raporta constatările urmând cele mai bune practici.

Cadrul modelului de moderare pe care l-ai învățat - testarea modului în care variabilele moderatoare influențează relațiile dintre predictori și rezultate - este fundamental pentru cercetarea statistică avansată. Înțelegând asumpțiile analizei de moderare, interpretând corect efectele moderatoare și recunoscând când există moderare în datele tale, ești echipat să răspunzi la întrebări de cercetare sofisticate "pentru cine" și "în ce condiții".

Amintește-ți, fiecare set de date și întrebare de cercetare este unică, așa că adaptează aceste tehnici de analiză de moderare pentru a se potrivi nevoilor tale specifice. Moderarea în R este doar o abordare analitică puternică - combină-o cu alte metode pentru a dezvălui povestea completă în datele tale.

Dacă ai găsit informativ acest ghid de analiză de moderare și dorești să explorezi tehnici înrudite, verifică articolul nostru despre Cum Să Efectuezi Analiza de Mediere în R. Analiza de mediere te ajută să înțelegi 'cum' și 'de ce' ale relațiilor, în timp ce analiza de moderare dezvăluie 'când' și 'pentru cine' - împreună, oferă perspective cuprinzătoare asupra relațiilor dintre variabile.

Până atunci, analiză plăcută!