Analiza de moderare te ajută să înțelegi când se schimbă relația dintre două variabile. În loc să întrebi dacă X afectează Y, analiza de moderare întreabă: „Depinde intensitatea relației X→Y de o a treia variabilă (moderatorul)?"
În acest ghid, vei învăța două metode practice pentru a efectua analiza de moderare în SPSS: abordarea manuală cu standardizarea variabilelor și metoda modernă cu PROCESS Macro.
Ce Este Analiza de Moderare?
Analiza de moderare testează dacă relația dintre o variabilă independentă (X) și o variabilă dependentă (Y) se schimbă în funcție de nivelul unei a treia variabile numită moderator (M).
Gândește-te astfel: Efectul lui X asupra lui Y nu este același pentru toți. El depinde de M.
Exemplu de întrebare de cercetare: „Vârsta (M) moderează relația dintre calitatea relației cu clientul (X) și loialitatea consumatorului (Y)?"
În acest exemplu:
- Variabila Independentă (X): Calitatea Relației cu Clientul
- Variabila Moderatoare (M): Vârsta
- Variabila Dependentă (Y): Loialitatea Consumatorului
Întrebarea de cercetare este: Relația dintre calitatea relației și loialitate este mai puternică sau mai slabă pentru clienții mai în vârstă comparativ cu cei mai tineri?
Înțelegerea Moderării vs. Medierii
Moderarea este fundamental diferită de mediere:
Moderarea: M schimbă intensitatea sau direcția relației X→Y (efect de interacțiune)
Medierea: M transmite efectul de la X la Y (efect indirect)
În moderare, M nu are o relație cauzală cu X. Moderatorul este independent de predictor.
Află mai multe: Analiza de Mediere în SPSS
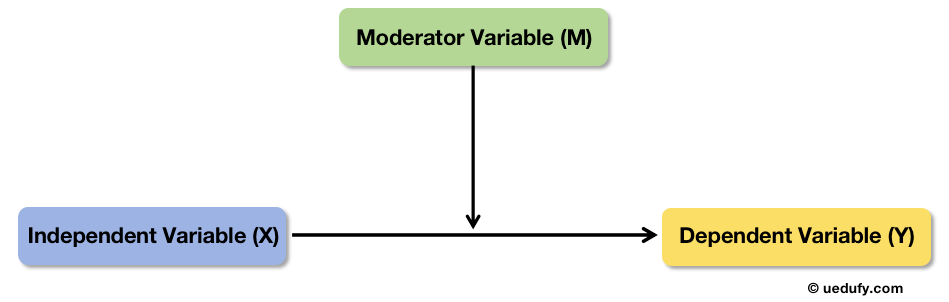 Diagrama conceptuală a moderării care arată cum M influențează intensitatea relației X→Y.
Diagrama conceptuală a moderării care arată cum M influențează intensitatea relației X→Y.
Termenul de Interacțiune
Moderarea este testată folosind un termen de interacțiune (numit și termen produs), calculat ca:
Interacțiune = X × M
Când incluzi acest termen de interacțiune într-un model de regresie, un efect de interacțiune semnificativ indică moderare.
Metoda 1: Analiza de Moderare Manuală
Metoda manuală necesită mai mulți pași dar te ajută să înțelegi mecanica de bază a analizei de moderare. Această abordare implică standardizarea variabilelor, crearea unui termen de interacțiune și rularea regresiei liniare.
Set de Date Exemplu:
Pentru acest tutorial, vom folosi un set de date cu trei variabile: Relație, Loialitate și Vârstă. Dacă vrei să urmărești, descarcă fișierul de date SPSS și importă-l în SPSS. Setul de date ar trebui să arate astfel:
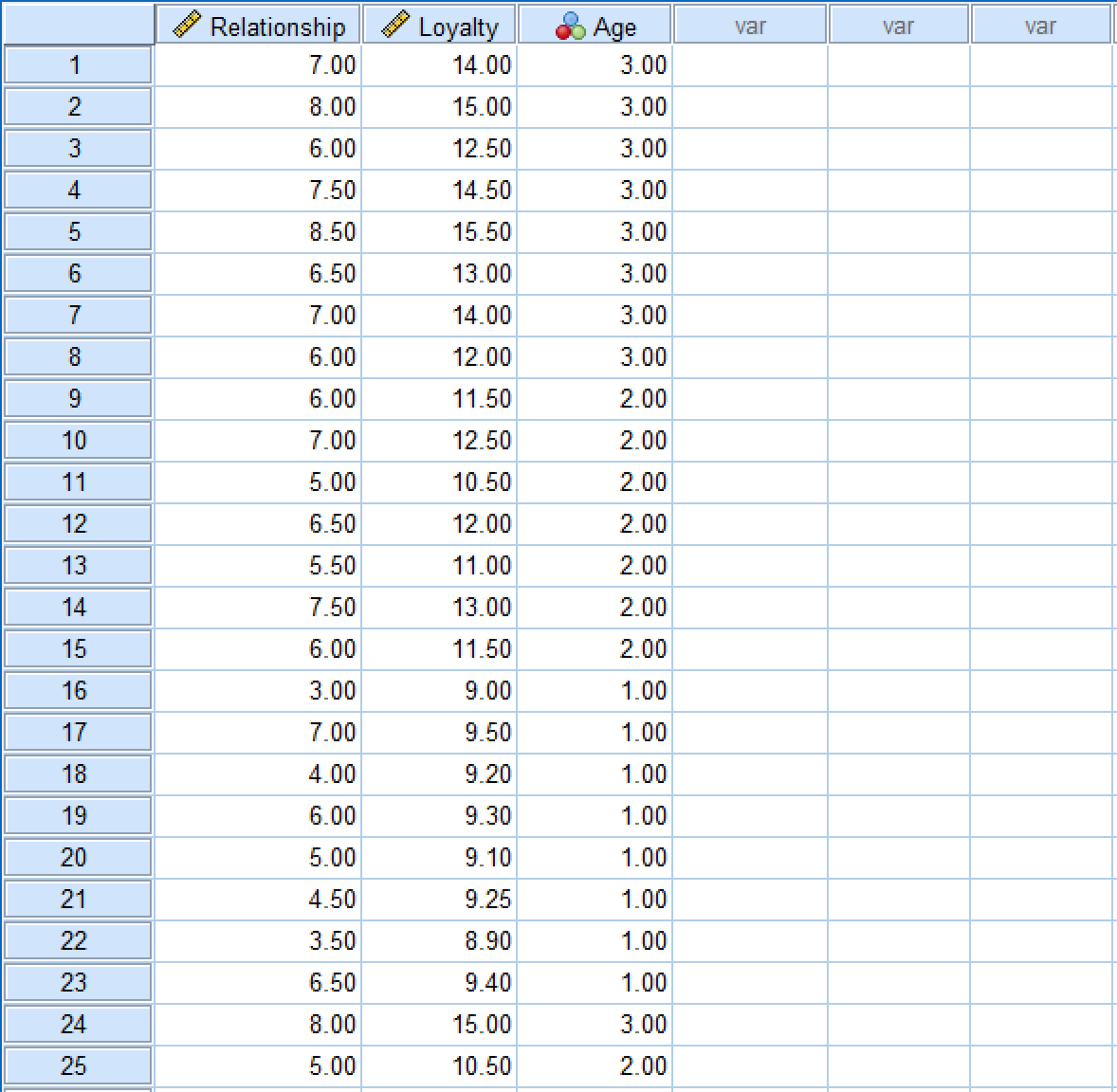 Set de date SPSS care arată variabilele Relationship, Loyalty și Age.
Set de date SPSS care arată variabilele Relationship, Loyalty și Age.
Pasul 1: Standardizează Variabilele Continue
Notă Importantă: În această metodă manuală, vom folosi standardizarea Z-score (creând scoruri standardizate cu medie = 0 și SD = 1). Aceasta este diferită de centrarea la medie folosită de PROCESS Macro, care doar scade media (medie = 0 dar păstrează SD-ul original).
Ambele abordări reduc multicolinearitatea dintre termenul de interacțiune și componentele sale. Standardizarea Z-score are avantajul de a pune toate variabilele pe aceeași scară, făcând coeficienții direct comparabili.
De ce să standardizezi? Când înmulțești X × M pentru a crea termenul de interacțiune, variabila rezultată este adesea foarte corelată cu X și M. Standardizarea minimizează această problemă și face interpretarea mai ușoară.
Pentru a standardiza variabilele din setul nostru de date, navighează la Analyze → Descriptive Statistics → Descriptives în meniul superior SPSS.
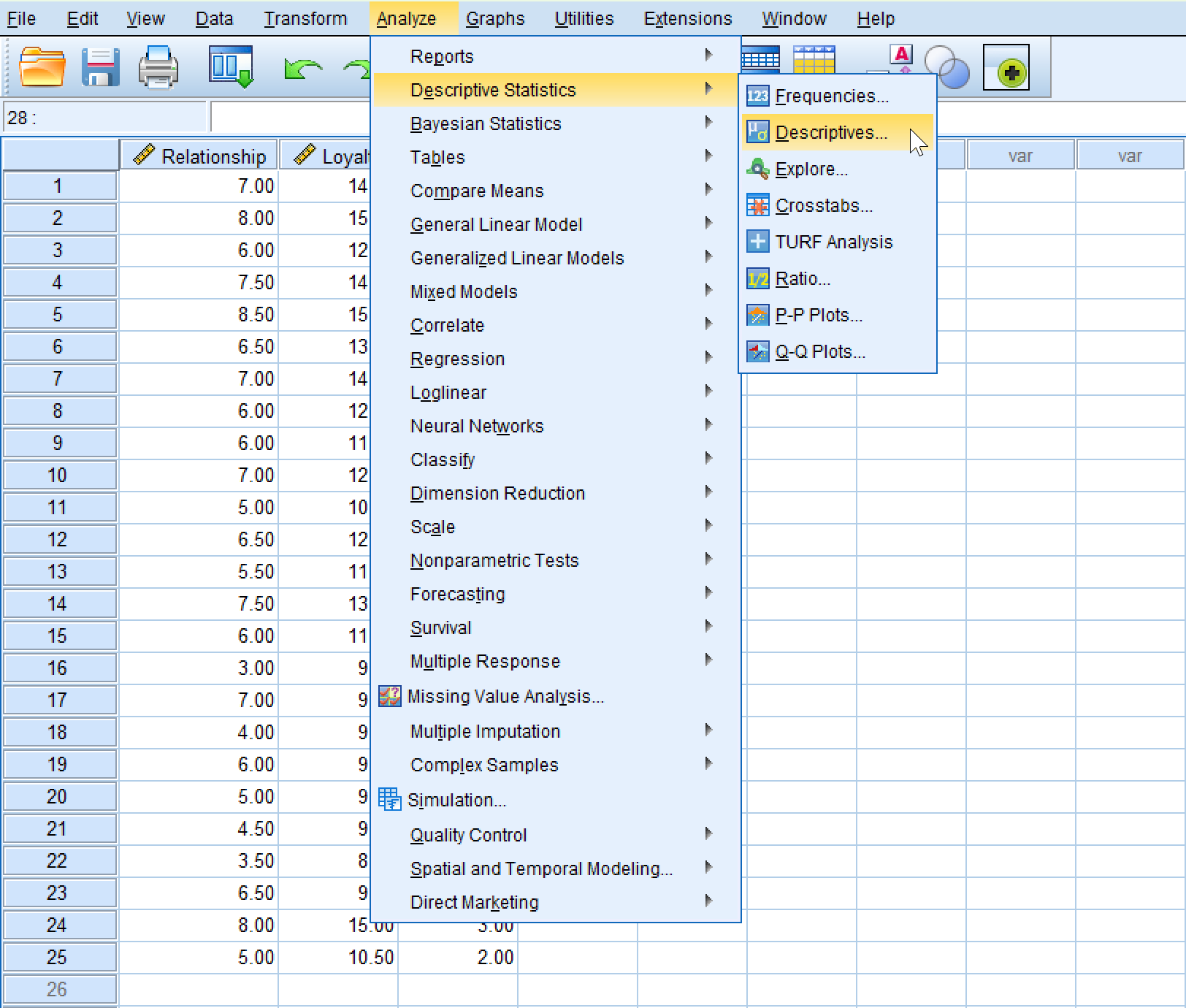 Navigarea către Descriptive Statistics în SPSS pentru centrarea variabilelor.
Navigarea către Descriptive Statistics în SPSS pentru centrarea variabilelor.
În fereastra Descriptives:
- Mută Relationship și Age în caseta Variable(s)
- Bifează „Save standardized values as variables"
- Click
OK
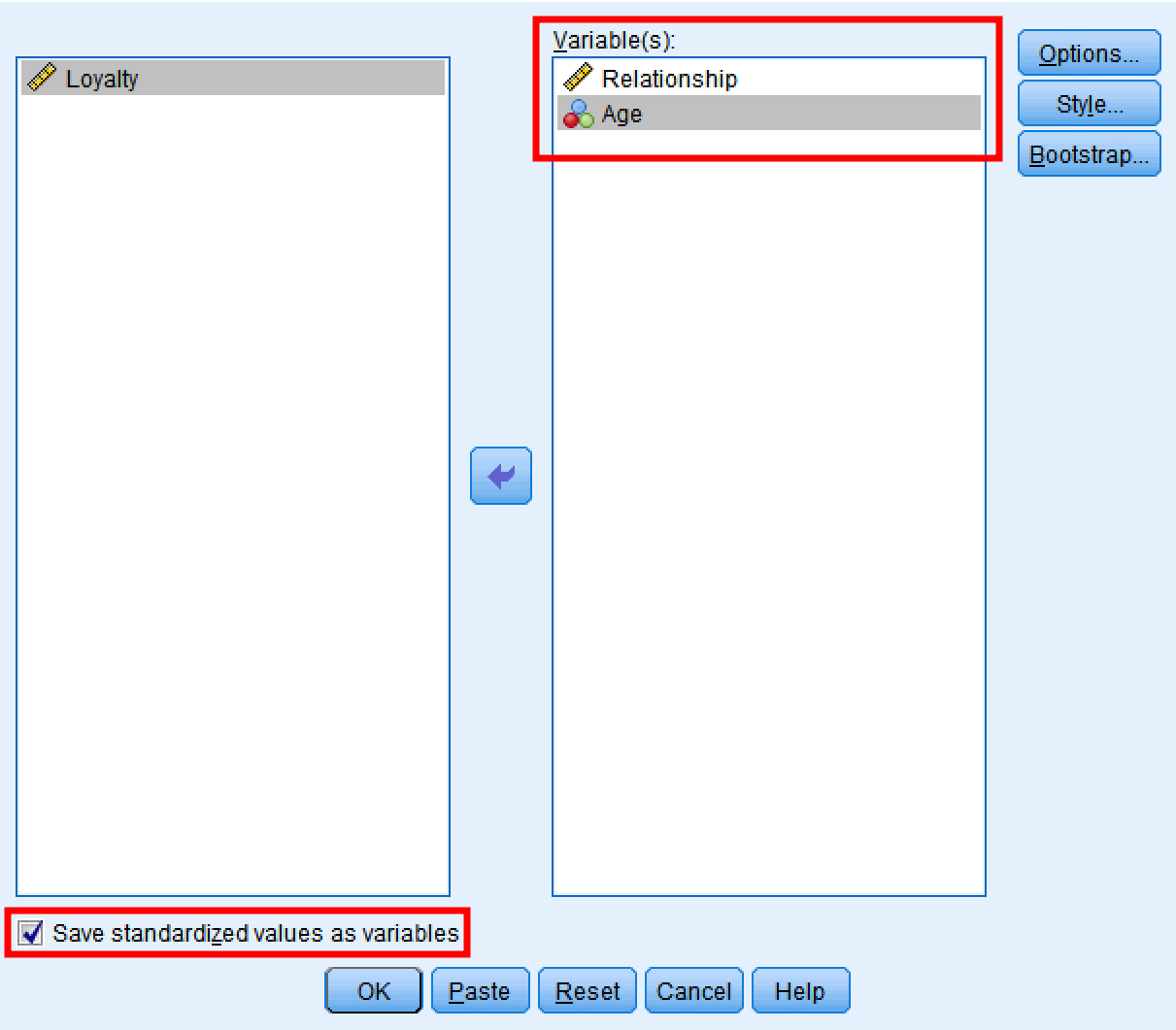 Fereastra de dialog SPSS Descriptives care arată selecția variabilelor și opțiunile de standardizare.
Fereastra de dialog SPSS Descriptives care arată selecția variabilelor și opțiunile de standardizare.
SPSS va crea variabile noi cu prefixul Z: ZRelationship și ZAge.
 SPSS Data View care arată variabilele originale și standardizate cu prefixul Z.
SPSS Data View care arată variabilele originale și standardizate cu prefixul Z.
Ce face standardizarea:
| Înainte de Standardizare | După Standardizare |
|---|---|
| Scară originală (ex., 1-7) | Scară Z-score (medie = 0, SD = 1) |
| Media variază per variabilă | Media = 0 pentru toate variabilele |
| Unități diferite | Unități standardizate |
Pasul 2: Creează Termenul de Interacțiune
Acum creează termenul produs înmulțind variabilele standardizate.
În SPSS:
- Mergi la
Transform→Compute Variable - În Target Variable, tastează:
INT(prescurtare de la interaction term) - În caseta Numeric Expression, tastează:
ZRelationship * ZAge - Click
OK
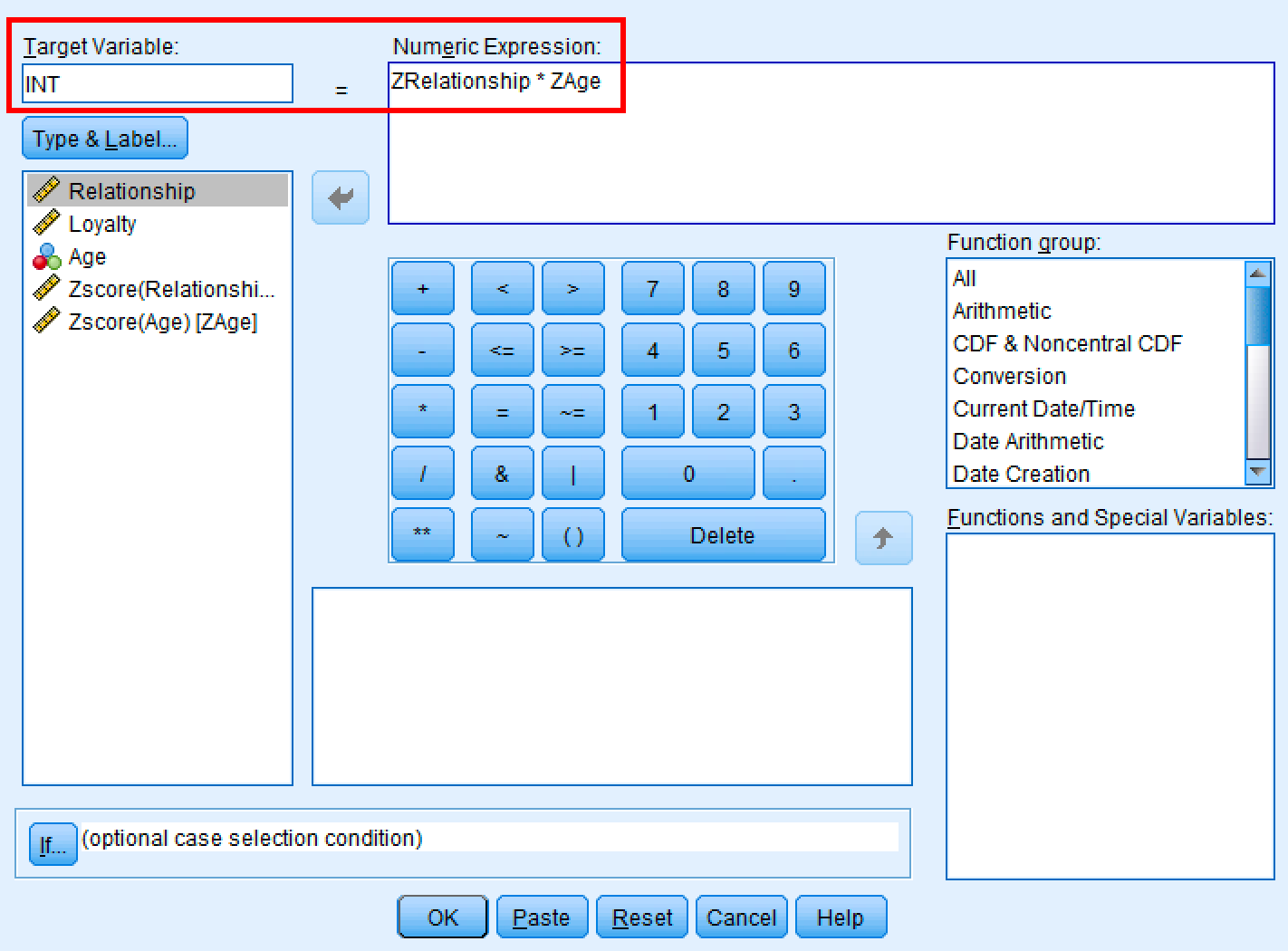 Fereastra de dialog SPSS Compute Variable pentru crearea termenului de interacțiune.
Fereastra de dialog SPSS Compute Variable pentru crearea termenului de interacțiune.
SPSS creează o variabilă nouă numită INT care conține produsul celor două variabile standardizate.
 SPSS Data View care arată variabila INT nou creată.
SPSS Data View care arată variabila INT nou creată.
Pasul 3: Rulează Regresia Liniară
Acum testează dacă termenul de interacțiune prezice semnificativ variabila dependentă.
În SPSS:
- Mergi la
Analyze→Regression→Linear - Mută Loyalty (Y) în caseta Dependent
- Mută ZRelationship, ZAge și INT în caseta Independent(s)
- Click
OK
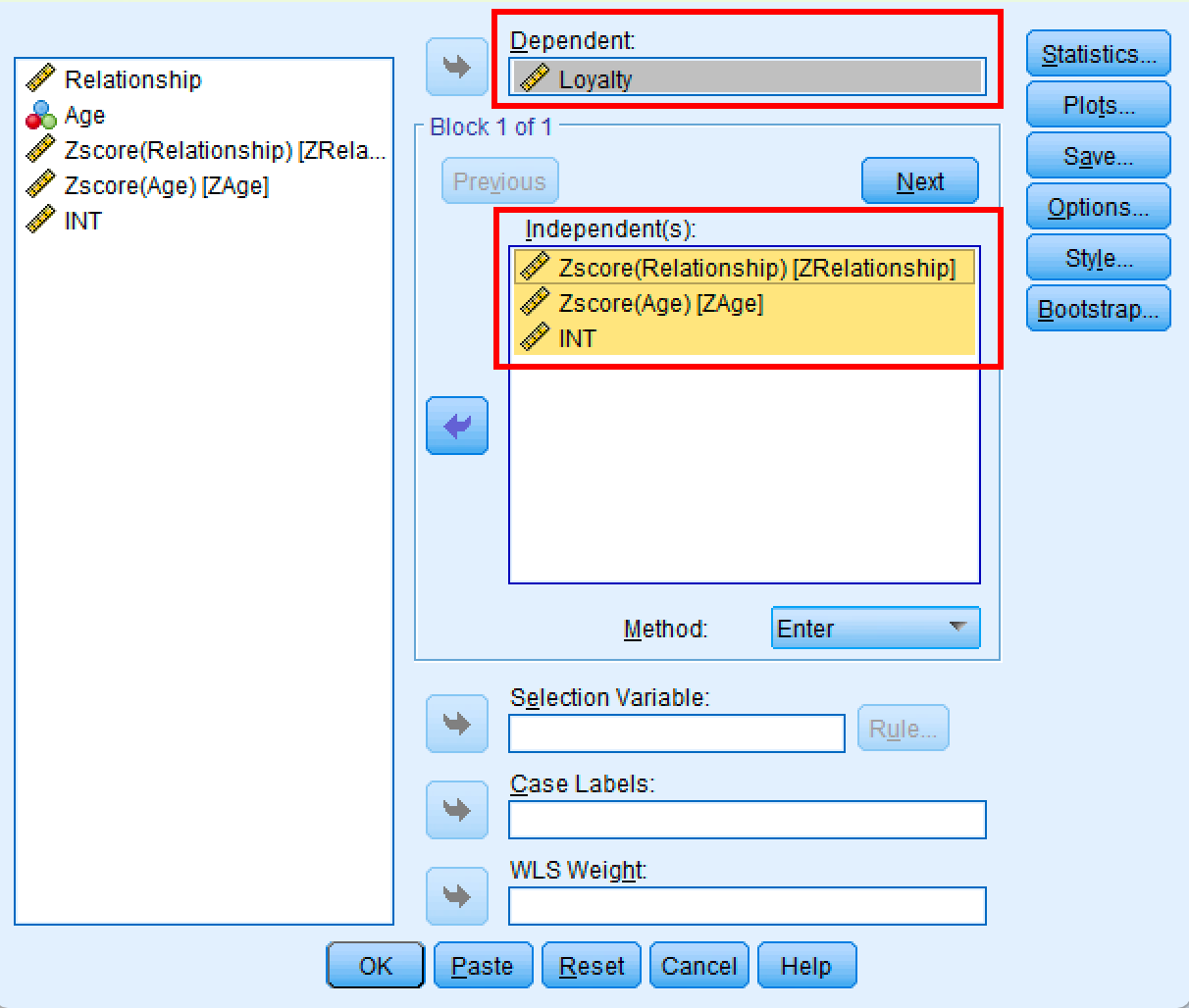 Fereastra de dialog SPSS Linear Regression pentru analiza de moderare.
Fereastra de dialog SPSS Linear Regression pentru analiza de moderare.
Interpretează Analiza de Moderare în SPSS
Analiza de regresie liniară produce trei tabele: Model Summary, ANOVA și Coefficients. Pentru a determina dacă Vârsta moderează relația dintre Relație și Loialitate, trebuie să examinezi valoarea de semnificație în tabelul Coefficients.
Pasul 1: Verifică Tabelul Model Summary
Mai întâi, uită-te la valoarea R Square din tabelul Model Summary.
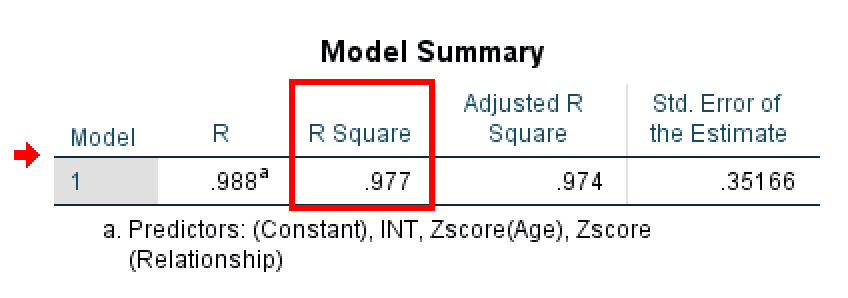 Tabelul Model Summary care arată valoarea R-squared pentru modelul de moderare.
Tabelul Model Summary care arată valoarea R-squared pentru modelul de moderare.
R Square îți spune cât de multă varianță din variabila dependentă (Loyalty) este explicată de modelul tău. În acest exemplu, R Square = 0.977, ceea ce înseamnă că modelul explică 97.7% din variația în loialitatea clienților.
⚠️ Notă Importantă Despre Acest Exemplu: Această valoare R² de 0.977 este artificial ridicată deoarece acestea sunt date simulate create în scopuri didactice. În cercetarea reală, valorile R² pentru modelele de moderare variază de obicei între 0.20 și 0.60. Nu te aștepta să vezi valori R² atât de mari în cercetarea ta reală.
Pasul 2: Verifică Tabelul ANOVA
Apoi, examinează tabelul ANOVA pentru a testa dacă modelul tău de regresie general este semnificativ statistic.
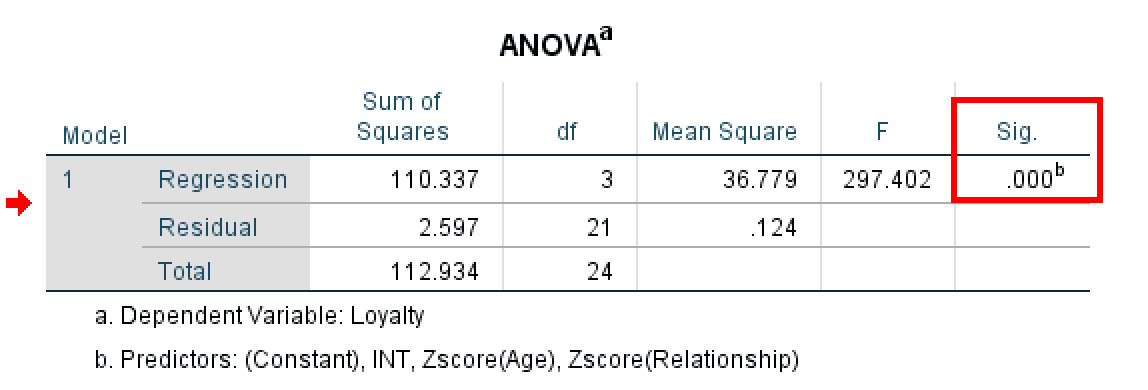 Tabelul ANOVA care arată semnificația modelului general.
Tabelul ANOVA care arată semnificația modelului general.
Tabelul ANOVA testează dacă modelul tău de regresie (cu toți predictorii incluși) explică o cantitate semnificativă statistic de varianță în variabila outcome. Uită-te la coloana Sig.:
- Dacă Sig. < 0.05 (adesea arătat ca 0.000): Modelul tău este semnificativ statistic. Cel puțin unul dintre predictorii tăi are un efect semnificativ asupra Loyalty.
- Dacă Sig. > 0.05: Modelul tău nu este semnificativ. Predictorii nu explică semnificativ variația în outcome.
În acest exemplu, tabelul ANOVA arată F = 297.402 cu Sig. = .000 (p < 0.001). Acest rezultat foarte semnificativ confirmă că modelul general este semnificativ statistic.
Pasul 3: Examinează Tabelul Coefficients
În final, verifică tabelul Coefficients pentru a vedea dacă termenul de interacțiune (INT) este semnificativ.
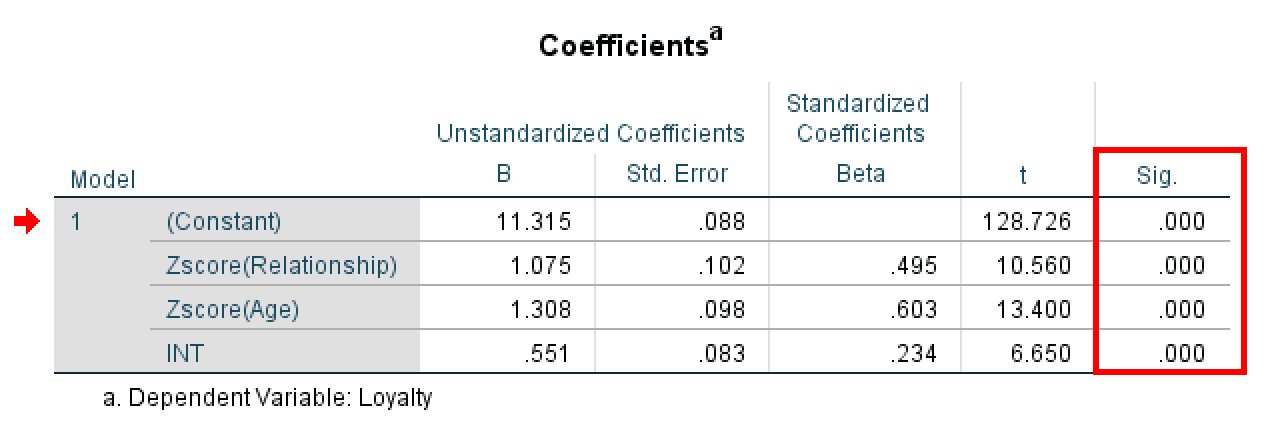 Tabelul SPSS regression coefficients care arată efectul de interacțiune.
Tabelul SPSS regression coefficients care arată efectul de interacțiune.
Înainte de a interpreta rezultatele, să înțelegem ce îți spune fiecare rând din tabelul Coefficients:
| Variabilă | Ce Îți Spune |
|---|---|
| (Constant) | Valoarea de bază a Loyalty când toți predictorii sunt zero |
| Zscore(Relationship) | Efectul principal al calității relației asupra loialității |
| Zscore(Age) | Efectul principal al vârstei asupra loialității |
| INT | Efectul de moderare: se schimbă relația dintre X și Y în funcție de vârstă? |
Acum, uită-te la rândul pentru INT (termenul tău de interacțiune) și verifică coloana Sig.:
- Dacă Sig. < 0.05: Variabila moderatoare (Age) afectează semnificativ relația dintre Relationship și Loyalty. Moderarea există.
- Dacă Sig. > 0.05: Age nu moderează relația. Nu există efect de moderare.
În acest exemplu, valoarea Sig. pentru INT este .000 (p < 0.001). Aceasta este foarte semnificativă, mult sub pragul de 0.05. Putem concluziona cu încredere că efectul de moderare este semnificativ statistic.
Pasul 4: Interpretează Direcția
Odată ce ai confirmat că interacțiunea este semnificativă, trebuie să înțelegi direcția efectului de moderare. Uită-te la valoarea B (coeficient nestandardizat) în rândul INT.
În acest exemplu, valoarea B pentru INT este 0.551. Deoarece acesta este un coeficient pozitiv, ne spune că relația dintre Relationship și Loyalty devine mai puternică pe măsură ce Age crește.
Ce Înseamnă Aceasta:
Coeficientul pozitiv (B = 0.551) indică faptul că efectul calității relației asupra loialității este mai puternic pentru clienții mai în vârstă decât pentru clienții mai tineri.
Înțelegerea Coeficienților Pozitivi vs. Negativi:
- Coeficient pozitiv (+): Relația X→Y devine mai puternică pe măsură ce M crește. Valorile mai mari ale moderatorului amplifică efectul.
- Coeficient negativ (−): Relația X→Y devine mai slabă pe măsură ce M crește. Valorile mai mari ale moderatorului diminuează efectul.
Metoda 2: PROCESS Macro (Recomandat)
PROCESS Macro, dezvoltat de Andrew Hayes, este standardul modern pentru analiza de moderare. Gestionează automat standardizarea, creează termeni de interacțiune și oferă efecte condiționale la diferite niveluri ale moderatorului.
Instalarea PROCESS Macro
Înainte de a putea folosi PROCESS, trebuie să îl instalezi în SPSS. Instalarea durează aproximativ 5 minute.
Pentru instrucțiuni detaliate de instalare, vezi ghidul nostru: Cum să Instalezi PROCESS Macro în SPSS.
Rularea Moderării cu PROCESS
Odată ce PROCESS este instalat, îl poți accesa din meniul SPSS.
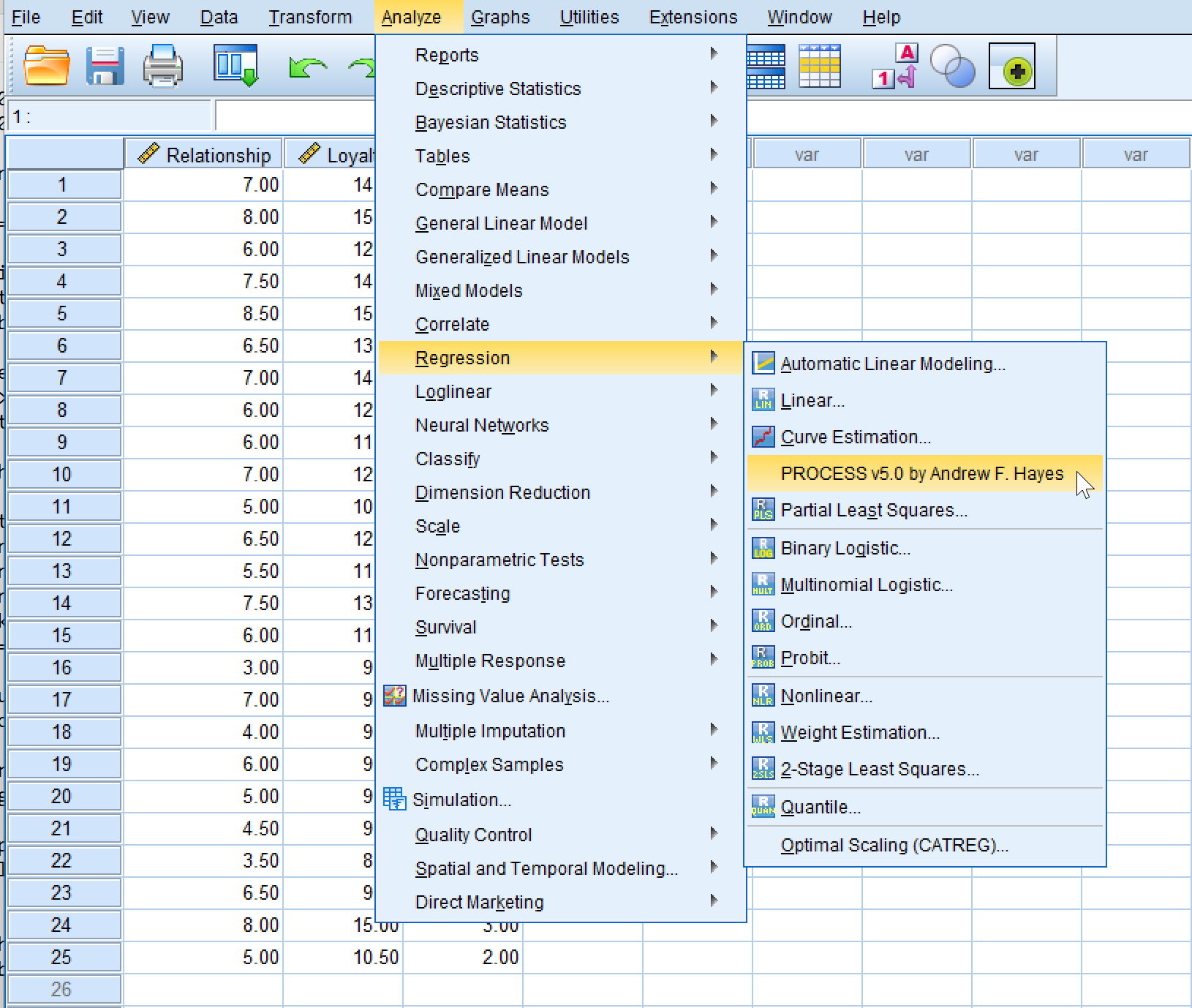 Accesarea PROCESS Macro din meniul SPSS: Analyze → Regression → PROCESS.
Accesarea PROCESS Macro din meniul SPSS: Analyze → Regression → PROCESS.
În SPSS:
- Mergi la
Analyze→Regression→PROCESS v5.0 by Andrew F. Hayes - Selectează Model 1 (modelul simplu de moderare)
- Mută Loyalty în caseta Y Variable
- Mută Relationship în caseta X Variable(s)
- Mută Age în caseta W: Primary Moderator (nu în caseta M: Mediator)
- Lasă M: Mediator(s), Z: Secondary Moderator și COV: Covariate(s) goale
- Click
Options
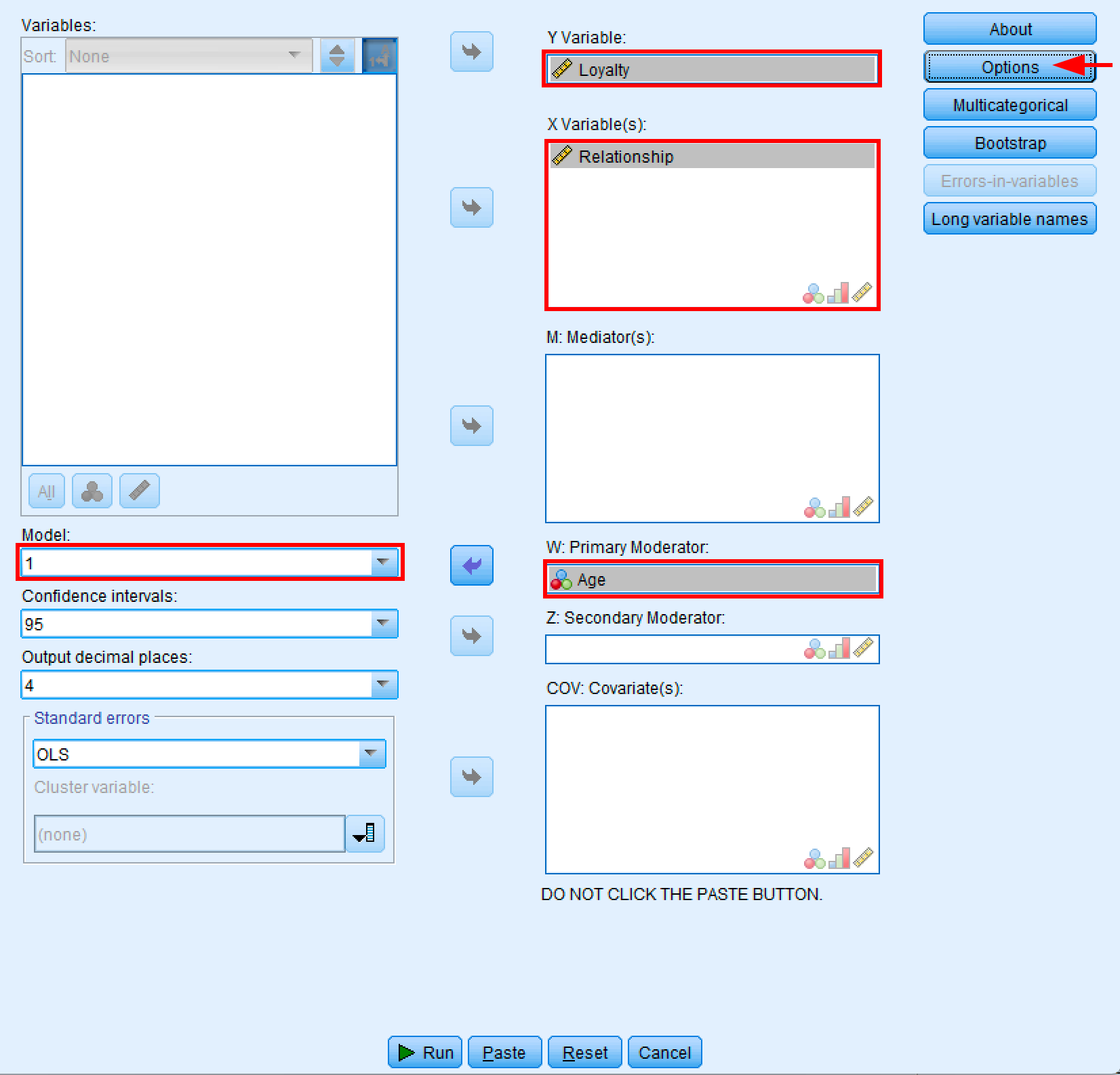 Fereastra de dialog PROCESS Macro configurată pentru analiza simplă de moderare folosind Model 1.
Fereastra de dialog PROCESS Macro configurată pentru analiza simplă de moderare folosind Model 1.
Important: Asigură-te că plasezi Age în caseta W: Primary Moderator, nu în caseta M: Mediator(s). Caseta M este pentru analiza de mediere (modele diferite), în timp ce caseta W este specific pentru moderare.
În fereastra Options:
- Sub „Centering for moderation:" asigură-te că este bifat „Mean center components of products"
- Sub „Probing moderation:" asigură-te că este bifat „Probe interactions"
- Bifează „Johnson-Neyman technique" pentru a identifica regiunile de semnificație
- Sub „Visualizing moderation:" bifează „Generate data to visualize moderation"
- Click
OK
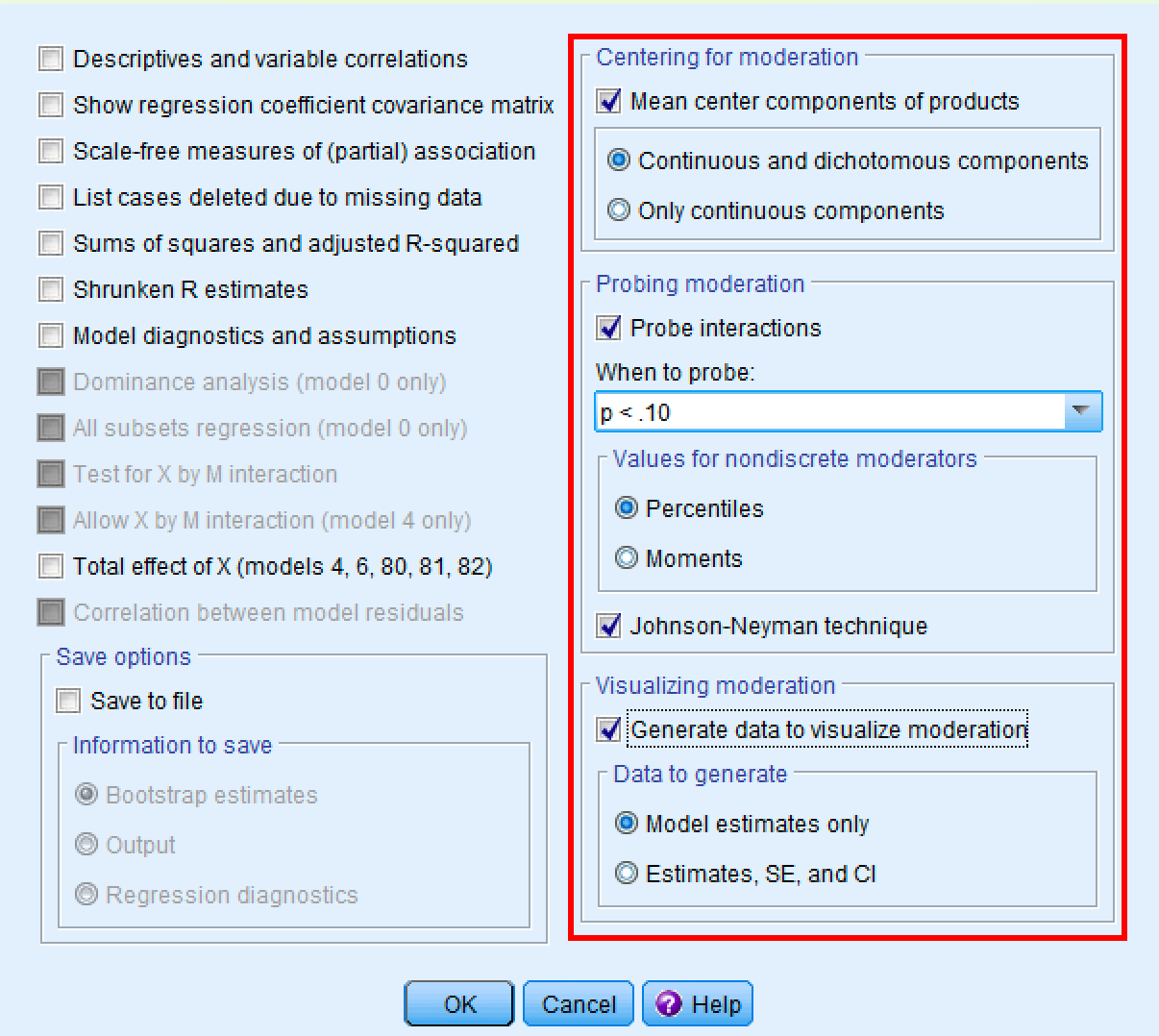 Fereastra de opțiuni PROCESS care arată setările recomandate pentru analiza de moderare.
Fereastra de opțiuni PROCESS care arată setările recomandate pentru analiza de moderare.
Odată ce ai configurat opțiunile, click butonul Run în fereastra principală PROCESS.
Înțelegerea Output-ului PROCESS
PROCESS produce aceleași tabele de regresie pe care le-ai văzut în Metoda 1, dar gestionează automat toate calculele.
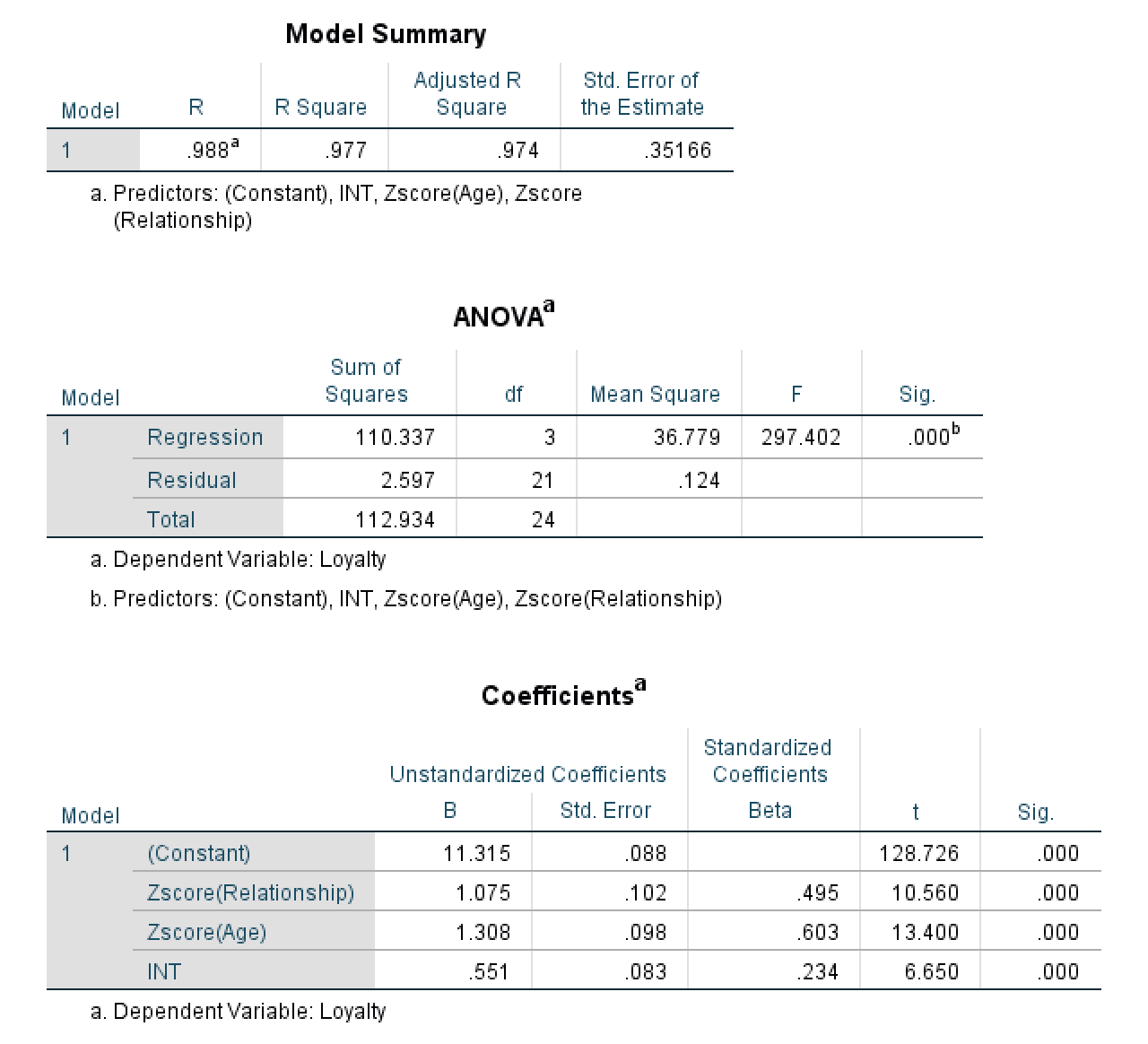 Output PROCESS care arată tabelele Model Summary, ANOVA și Coefficients.
Output PROCESS care arată tabelele Model Summary, ANOVA și Coefficients.
Rezultatele sunt identice cu Metoda 1 (R² = .977, F = 297.402, INT Sig. = .000), confirmând efectul semnificativ de moderare.
Ce Adaugă PROCESS În Plus Față de Metoda 1:
Avantajul real al PROCESS este output-ul suplimentar pe care îl oferă:
- Tabelul Efectelor Condiționale: Arată cum se schimbă efectul lui Relationship asupra lui Loyalty la diferite niveluri de Age (ex., scăzut, mediu, ridicat)
- Output-ul Johnson-Neyman: Identifică valorile exacte ale Age unde efectul de moderare devine semnificativ sau nesemnificativ
- Date de Vizualizare: Valori pre-calculate gata pentru reprezentarea grafică a interacțiunii
Interpretarea Simple Slopes (Efecte Condiționale)
Găsirea unui termen de interacțiune semnificativ îți spune că moderarea există, dar nu îți spune cum afectează moderatorul relația X→Y. Aici devine critică analiza simple slopes.
Ce Sunt Simple Slopes?
Simple slopes (numite și efecte condiționale) reprezintă relația dintre X și Y la valori specifice ale moderatorului. În loc să întrebi „Afectează moderatorul relația?" (răspuns dat de termenul de interacțiune), simple slopes răspund: „Care este relația X→Y la diferite niveluri ale moderatorului?"
Pentru exemplul nostru, simple slopes ne spun:
- Care este efectul lui Relationship asupra lui Loyalty pentru clienții mai tineri?
- Care este efectul lui Relationship asupra lui Loyalty pentru clienții de vârstă medie?
- Care este efectul lui Relationship asupra lui Loyalty pentru clienții mai în vârstă?
Cum să Interpretezi Simple Slopes
Folosind valorile din analiza noastră:
La Vârstă Scăzută (-1.04, clienți mai tineri):
- Effect = 0.2775, p = .0031
- Interpretare: Pentru clienții mai tineri, o creștere de o unitate în Calitatea Relației duce la o creștere de 0.28 unități în Loialitate. Această relație este semnificativă statistic.
La Vârstă Medie (-0.04, clienți de vârstă medie):
- Effect = 0.7414, p < .001
- Interpretare: Pentru clienții de vârstă medie, o creștere de o unitate în Calitatea Relației duce la o creștere de 0.74 unități în Loialitate. Acesta este un efect substanțial mai puternic decât pentru clienții mai tineri.
La Vârstă Ridicată (0.96, clienți mai în vârstă):
- Effect = 1.2052, p < .001
- Interpretare: Pentru clienții mai în vârstă, o creștere de o unitate în Calitatea Relației duce la o creștere de 1.21 unități în Loialitate. Acesta este cel mai puternic efect dintre toate grupele de vârstă.
Povestea Completă a Moderării
Combinând termenul de interacțiune și simple slopes:
- Termenul de interacțiune este semnificativ (β = 0.464, p < .001) → Vârsta moderează relația Relationship→Loyalty
- Toate cele trei simple slopes sunt pozitive și semnificative → Calitatea Relației crește Loialitatea la toate nivelurile de vârstă
- Simple slopes cresc de la 0.28 → 0.74 → 1.21 → Efectul devine progresiv mai puternic pe măsură ce vârsta crește
În limbaj simplu: Deși calitatea relației întotdeauna îmbunătățește loialitatea, contează mai mult pentru clienții mai în vârstă decât pentru cei mai tineri.
Compararea Celor Două Metode
| Caracteristică | Metoda Manuală | PROCESS Macro |
|---|---|---|
| Ușurința Utilizării | Necesită standardizare manuală și creare de variabile | Standardizare și calcul automate |
| Efecte Condiționale | Nu sunt furnizate | Calculat automat |
| Vizualizare | Necesită reprezentare grafică manuală | Oferă valori pentru reprezentare ușoară |
| Standardul Modern | Educațional | Cea mai bună practică actuală |
| Recomandare | Folosește pentru învățare | Folosește pentru cercetare |
Raportarea Rezultatelor de Moderare
Când raportezi rezultatele analizei de moderare, include:
- Potrivirea modelului general (R², F-statistic, semnificație)
- Efectele principale pentru X și M (coeficienți și semnificație)
- Efectul de interacțiune (coeficient B, t-statistic, p-value)
- Direcția moderării (coeficient pozitiv sau negativ)
Exemplu de Declarație a Rezultatelor:
„O analiză de moderare a fost efectuată pentru a testa dacă vârsta moderează relația dintre calitatea relației cu clientul și loialitate. Modelul general a fost semnificativ, F(3, 21) = 297.40, p < .001, R² = .977. Termenul de interacțiune a fost semnificativ (B = 0.551, t = 6.65, p < .001), indicând că vârsta moderează relația dintre calitatea relației și loialitate. Coeficientul pozitiv sugerează că efectul calității relației asupra loialității devine mai puternic pe măsură ce vârsta crește."
Considerații Importante
Cerințe pentru Dimensiunea Eșantionului
Efectele de interacțiune sunt notoriu dificil de detectat și necesită eșantioane mai mari decât doar efectele principale.
Recomandări minime:
- Efecte mici: 200+ participanți
- Efecte medii: 100-150 participanți
- Efecte mari: 50-80 participanți
Centrarea Este Recomandată
Este în general recomandat să centrezi variabilele continue (fie centrare la medie, fie standardizare Z-score) înainte de a crea termeni de interacțiune. Aceasta:
- Reduce multicolinearitatea între X, M și X×M
- Face efectele principale interpretabile ca efecte la media moderatorului
- Stabilizează estimările de regresie
Teoria Ar Trebui Să Ghideze Analiza
Nu testa pentru moderare doar pentru că poți. Ar trebui să ai:
- Justificare teoretică: De ce ar schimba M relația X→Y?
- Ipoteze a priori: Moderarea întărește sau slăbește?
- Interpretare substanțială: Ce înseamnă moderarea în practică?
Întrebări Frecvente
Concluzie
Ai învățat două metode pentru efectuarea analizei de moderare în SPSS:
- Metoda Manuală: Standardizează variabilele, creează termenul de interacțiune, rulează regresia (bună pentru învățare)
- PROCESS Macro: Analiză automatizată cu efecte condiționale și opțiuni robuste (cea mai bună pentru cercetare)
Pentru disertația sau proiectul tău de cercetare, recomandăm PROCESS Model 1 deoarece oferă centrare automată, efecte condiționale la niveluri multiple și opțiuni pentru standard errors robuste.
Ține minte: Analiza de moderare relevă când au loc relațiile, în timp ce medierea relevă cum sau de ce au loc relațiile. Înțelegerea acestei distincții este critică pentru alegerea analizei potrivite.
Pași Următori:
- Descarcă datele de practică și rulează ambele metode singur
- Învață analiza de mediere pentru a înțelege mecanismele: Analiza de Mediere în SPSS