Cum să Calculezi Eroarea Standard în Excel, SPSS și R: Formula & Exemple

În acest tutorial cuprinzător, vei învăța cum să calculezi eroarea standard în Excel, SPSS și R cu exemple pas cu pas și seturi de date descărcabile. Fie că trebuie să găsești eroarea standard în Excel folosind formule, să calculezi eroarea standard în SPSS cu statistici descriptive sau să o calculezi în R, acest ghid acoperă tot ce ai nevoie.

Vom acoperi formula erorii standard, interpretarea sa și calcule practice pe toate cele trei platforme cu exemple reale.

Notă: Termenii "eroare standard" și "eroarea standard estimată a mediei" sunt folosiți interschimbabil în statistică și se referă la același concept.

Ce Este Eroarea Standard a Mediei

Într-un scenariul ideal, cercetătorii ar avea acces la populații întregi pentru studiile lor. Cu toate acestea, acest lucru este rareori fezabil în practică.

În majoritatea cazurilor, colectăm date prin eșantionarea populației pe care o investigăm. Dacă luăm mai multe eșantioane din aceeași populație, vom observa că acestea sunt ușor diferite.

De exemplu, media fiecărui eșantion va fi diferită de altul, deoarece fiecare eșantion conține probabil membri diferiți ai aceleiași populații.

Deci, cum știm dacă datele eșantionului reprezintă întreaga populație?

Aici devine esențială eroarea standard a mediei (sau pur și simplu, eroarea standard). Iată notațiile comune folosite de diverși autori în literatura de specialitate:

$SE \qquad SEM \qquad SE(\bar{x}) \qquad SE_{\bar{x}} \qquad s_{\bar{x}}$

Eroarea standard este utilizată pentru a determina cât de aproape este media unui eșantion luat dintr-o populație comparativ cu valoarea medie a populației adevărate.

O valoare mai mică a erorii standard arată că mediile eșantionului au o distribuție apropiată în jurul mediei populației, fiind astfel mai reprezentative pentru populația adevărată.

În contrast, o valoare mai mare a erorii standard arată probabil că eșantionul este o reprezentare inexactă a populației adevărate.

Cea mai bună modalitate de a reduce o valoare mare a erorii standard este prin creșterea dimensiunii eșantionului. Vom face o comparație mai târziu în această lecție.

De asemenea, este important să folosești eșantionarea aleatoare atunci când colectezi datele pentru a evita prejudecata de eșantionare.

În cele din urmă, ar trebui să înțelegi cu adevărat diferența dintre eroarea standard a mediei și abaterea standard în statistică. Cele două sunt adesea o sursă de mare confuzie în rândul studenților.

Cum Să Găsești Eroarea Standard a Mediei

Formula de mai jos este ecuația pentru eroarea standard a mediei folosind abaterea standard a populației:

$\Large SE = \frac{\sigma}{\sqrt{n}}$

Unde:

$SE$ = Eroarea standard a mediei
$\sigma$ = Abaterea standard a populației
$n$ = Dimensiunea eșantionului
$\sqrt{n}$ = Rădăcina pătrată a dimensiunii eșantionului

Avertismentul aici este că trebuie să cunoaștem abaterea standard reală a populației pentru a putea calcula eroarea standard folosind formula de mai sus.

De obicei, populațiile sunt mari și este puțin probabil să avem acces la întreaga populație pentru a calcula valoarea abaterii standard a populației.

Ca și în majoritatea cazurilor în cercetare, eșantionarea unei populații este o abordare mult mai ușoară și mai puțin costisitoare. Din fericire, există o modalitate de a estima eroarea standard a mediei folosind abaterea standard a eșantionului. Iată formula:

$\Large SE = \frac{s}{\sqrt{n}}$

Unde:

$SE$ = Eroarea standard a mediei
$s$ = Abaterea standard a eșantionului
$n$ = Dimensiunea eșantionului
$\sqrt{n}$ = Rădăcina pătrată a dimensiunii eșantionului

S-ar putea să fi observat că ambele formule pentru eroarea standard de mai sus sunt destul de similare. Într-adevăr, singura diferență fiind dacă cunoaștem sau nu valoarea pentru abaterea standard a populației.

Cum Să Calculezi Eroarea Standard

Pentru a calcula eroarea standard, urmează acești pași simpli:

Calculează sau obține abaterea ta standard (s pentru eșantion, σ pentru populație)
Numără dimensiunea eșantionului tău (n)
Calculează rădăcina pătrată a dimensiunii eșantionului tău (√n)
Împarte abaterea standard la √n pentru a obține eroarea standard

Formula erorii standard este: SE = s / √n (pentru date eșantion) sau SE = σ / √n (pentru date populație).

În practică, poți calcula eroarea standard folosind:

Excel: =STDEV(interval)/SQRT(COUNT(interval))
SPSS: Analizează → Statistici Descriptive → Explorează (pași detaliate mai jos)
R: stderr <- function(x) sd(x)/sqrt(length(x)) (pași detaliate mai jos)

Acum că știm ecuațiile pentru eroarea standard, să facem niște matematică de bază și să învățăm cum să calculăm eroarea standard manual.

Exemplul 1: Presupunând că știm că abaterea standard reală a unei populații constând din studenți care susțin examenul final este 7. Am luat de asemenea un eșantion aleatoriu de 100 de respondenți din această populație. Prin urmare avem:

\sigma = 7, \quad N = 100

Deoarece în acest exemplu de eroare standard știm valoarea abaterii standard reale, vom folosi prima ecuație pentru eroarea standard de mai sus, respectiv:

SE = \frac{\sigma}{\sqrt{n}}

După ce introducem numerele în ecuație avem:

SE = \frac{7}{\sqrt{100}} = \frac{7}{10} = 0.70

Deci, cum interpretăm rezultatul erorii standard în acest exemplu? Înseamnă pur și simplu că atunci când luăm un eșantion aleatoriu de N = 100 din această populație, diferența medie între mediile eșantionului și media populației este 0.70.

Exemplul 2: Acum, să presupunem că nu cunoaștem abaterea standard a populației studenților care susțin examenul final în școala noastră. În schimb, cunoaștem abaterea standard a eșantionului (S) pe care să o presupunem că este 5. Eșantionul (N) rămâne neschimbat, respectiv 100. Prin urmare avem:

s = 5, \quad N = 100

De această dată vom folosi ecuația pentru abaterea standard a eșantionului:

SE = \frac{s}{\sqrt{n}}

După ce inserăm numerele avem:

SE = \frac{5}{\sqrt{100}} = \frac{5}{10} = 0.50

Putem interpreta acest rezultat ca diferența medie între mediile eșantionului și media populației atunci când eșantionul este selectat aleatoriu și N = 100 este 0.50.

Eroarea standard a mediei este o măsură a diferenței pe care te aștepți să o obții între o statistică a eșantionului și parametrul populației și mediile eșantionului și media populației atunci când eșantioanele sunt selectate aleatoriu și de o dimensiune dată.

Calculează Eroarea Standard în SPSS

Există numeroase modalități de a găsi eroarea standard în SPSS. În această secțiune, ne vom concentra pe două metode eficiente.

Vrei să urmărești? Descarcă setul de date SPSS pentru practică din bara laterală, apoi lansează SPSS pe computer și navighează la File → Open → Data pentru a importa fișierul .sav.

(1) Calculează Eroarea Standard a Mediei în SPSS folosind Analiza Explorare

În meniul superior SPSS, navighează la Analyze → Descriptive Statistics → Explore

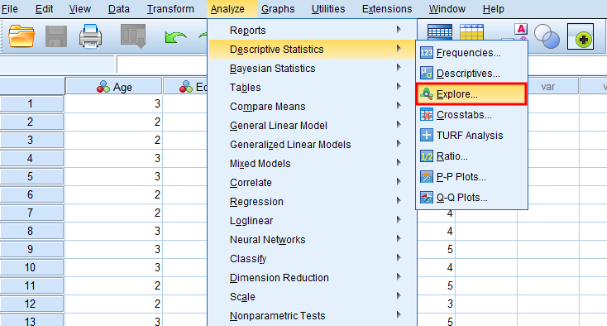
Meniul SPSS arătând calea de navigare Analyze apoi Descriptive Statistics apoi Explore pentru calcularea erorii standard

Navighează la Analyze → Descriptive Statistics → Explore în SPSS.

În fereastra Explore, selectează o variabilă din caseta din stânga și fă clic pe butonul săgeată pentru a o adăuga la Dependent List.

Caseta de dialog SPSS Explore arătând lista de variabile în stânga cu butonul săgeată pentru a muta variabile la Dependent List

Selectează variabila ta și fă clic pe butonul săgeată pentru a o adăuga la Dependent List.

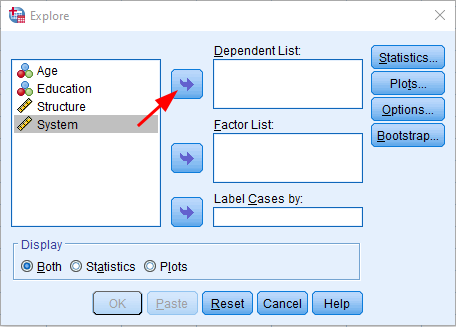
Fă clic pe butonul OK pentru a continua cu analiza.

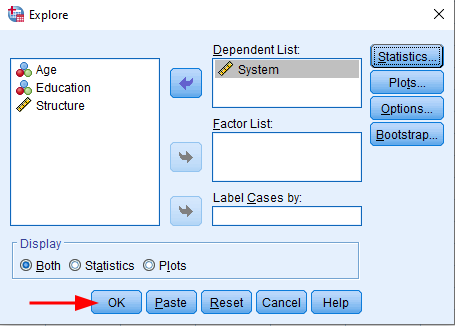
Fereastra SPSS Explore cu butonul OK evidențiat gata să ruleze analiza erorii standard

Fă clic pe OK pentru a executa analiza Explore.

În fereastra Output, derulează în jos la tabelul Descriptive. Pe rândul Mean, verifică coloana Std. Error pentru a găsi valoarea erorii standard pentru variabila respectivă.

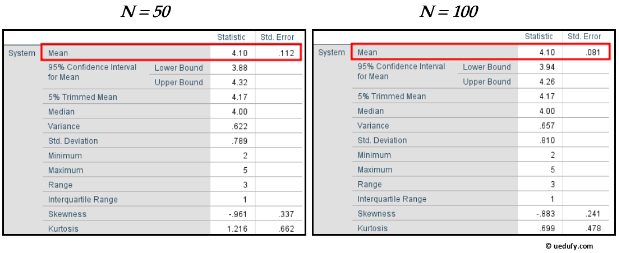
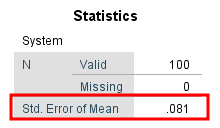
În exemplul nostru, media pentru variabila System este 4.10 și eroarea standard este 0.081.

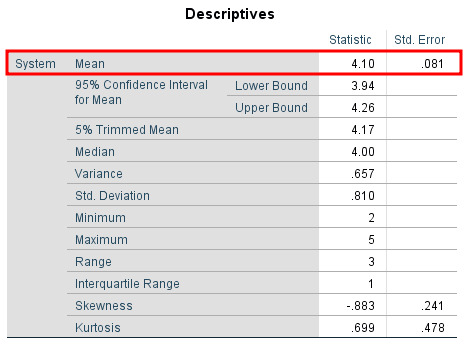
Tabelul de ieșire SPSS Descriptives arătând Media de 4.10 cu Std. Error de 0.081 pentru variabila System

Tabelul SPSS Descriptives arătând valoarea erorii standard de 0.081 în coloana Std. Error.

Această valoare a erorii standard este destul de scăzută, ceea ce înseamnă că mediile eșantionului analizate sunt distribuite strâns în jurul mediei populației. Cu alte cuvinte, eșantionul nostru este reprezentativ pentru populația din care a fost luat.

Dacă eroarea standard a mediei în analiza ta este mare, creșterea dimensiunii eșantionului prin selecție aleatorie va reduce probabil valoarea erorii standard.

De exemplu, dacă dimensiunea eșantionului tău este N = 50, ai putea să o crești la N = 100 sau mai mult pentru a reduce eroarea standard, așa cum se vede în comparația alăturată de mai jos.

Acordă atenție mediei și erorii standard a mediei în ambele figuri.

Comparație alăturată a rezultatelor SPSS arătând eroare standard mai mică cu N=100 versus dimensiunea eșantionului N=50

Comparație arătând cum scade eroarea standard pe măsură ce dimensiunea eșantionului crește de la N=50 la N=100.

(2) Găsește Eroarea Standard a Mediei în SPSS folosind Analiza Frecvențelor

O altă modalitate de a calcula eroarea standard în SPSS este folosind analiza Frecvențelor. În SPSS, navighează la Analysis → Descriptive Statistics → Frequencies

Meniul SPSS arătând calea de navigare Analyze apoi Descriptive Statistics apoi Frequencies pentru calcularea erorii standard

Navighează la Analyze → Descriptive Statistics → Frequencies în SPSS.

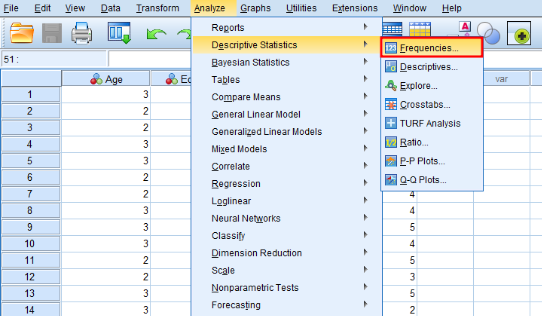
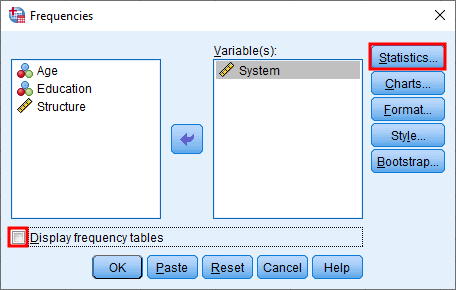
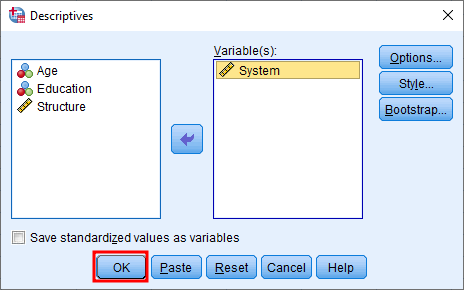
În fereastra Frequencies, adaugă variabila de interes din caseta din stânga la Variable(s). Debifează caseta Display frequency table și fă clic pe butonul Statistics.

Caseta de dialog SPSS Frequencies arătând selecția variabilelor cu Display frequency table debifat și butonul Statistics

Adaugă variabila ta la Variable(s), debifează Display frequency table și fă clic pe Statistics.

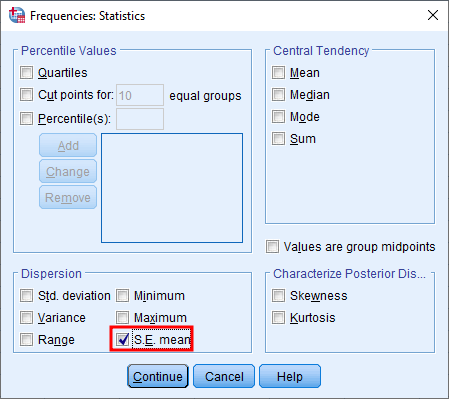
În fereastra Statistics, asigură-te că caseta S.E. mean este selectată și apasă butonul Continue.

Fereastra SPSS Frequencies Statistics cu caseta S.E. mean selectată pentru calcularea erorii standard

Selectează caseta S.E. mean și fă clic pe Continue.

Fă clic pe OK în fereastra Frequencies pentru a continua cu analiza erorii standard.

Fereastra SPSS Frequencies cu butonul OK gata să execute analiza erorii standard

Fă clic pe OK pentru a rula analiza Frequencies.

Valoarea erorii standard va fi afișată în rândul Std. Error of Mean al tabelului Statistics

Tabelul de ieșire SPSS Statistics arătând valoarea Std. Error of Mean din analiza Frequencies

Rezultatul erorii standard apare în rândul Std. Error of Mean al tabelului Statistics.

Calculul Erorii Standard în Excel

Pentru a găsi eroarea standard a mediei în Excel, trebuie pur și simplu să traducem formula erorii standard în sintaxa Excel: eroare standard = abatere standard / rădăcina pătrată a numărului total de eșantioane N.

Set de date pentru practică disponibil: Descarcă fișierul Excel din bara laterală pentru a urmări acest exemplu.

Iată cum să o calculezi:

Pe setul de date Excel, fă clic pe o celulă goală oriunde pe foaia de calcul

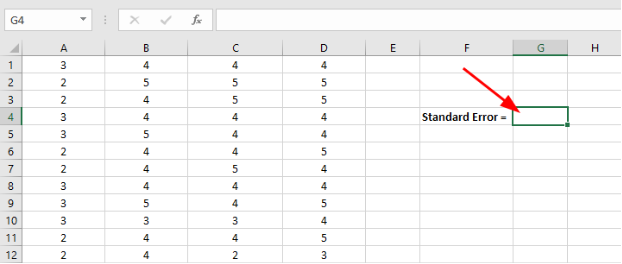
Foi de calcul Excel arătând date în rânduri cu celulă goală selectată pentru introducerea formulei erorii standard

Fă clic pe o celulă goală în Excel unde dorești să apară rezultatul erorii standard.

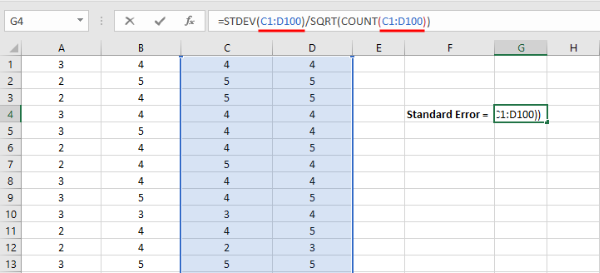
Copiază formula Excel pentru eroarea standard de mai jos în câmpul Insert Function din Excel.

=STDEV(interval eșantionare)/SQRT(COUNT(interval eșantionare))

Bara de formule Excel arătând formula erorii standard STDEV împărțit la SQRT din COUNT pentru calcularea erorii standard

Introdu formula erorii standard: =STDEV(interval eșantionare)/SQRT(COUNT(interval eșantionare)).

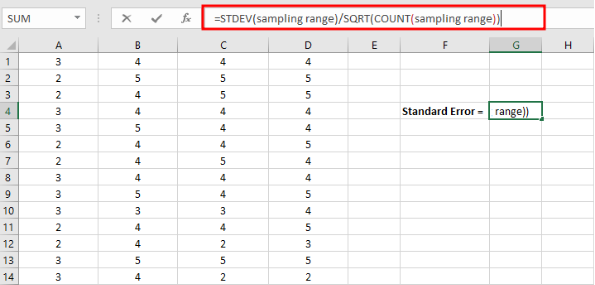
Înlocuiește intervalul eșantionare din formula Excel pentru eroarea standard cu intervalul real de celule pe care dorești să îl incluzi în analiza ta.

Odată ce selecția ta este făcută, apasă tasta ENTER pentru a finaliza analiza.

Formula Excel cu intervalul real de celule A2:A101 înlocuind placeholder-ul intervalului eșantionare în calculul erorii standard

Înlocuiește "intervalul eșantionare" cu intervalul tău real de celule (de ex., A2:A101) și apasă ENTER.

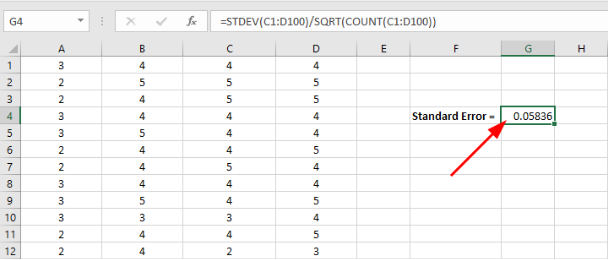
Excel va afișa rezultatul erorii standard în celula respectivă, așa cum se vede în captura de mai jos.

Celula Excel afișând rezultatul calculat al erorii standard după executarea formulei

Excel afișează valoarea calculată a erorii standard în celula selectată.

Calculul Erorii Standard În R

În cele din urmă, să aruncăm o privire la ce funcție putem folosi pentru a găsi eroarea standard a mediei în R.

Așa cum am discutat mai devreme, eroarea standard a mediei este doar abaterea standard împărțită la rădăcina pătrată a dimensiunii eșantionului.

Pentru acest exemplu voi folosi același set de date Excel pe care l-am folosit în secțiunea anterioară.

Lansează RStudio pe computer. În meniul superior R, navighează la File → Import Dataset → From Excel.

În fereastra Import Excel Data în R, fă clic pe Browse și selectează fișierul dataset.xlsx pe care l-ai descărcat mai sus. Fă clic pe Open apoi pe butonul Import pentru a finaliza importarea setului de date Excel în R.

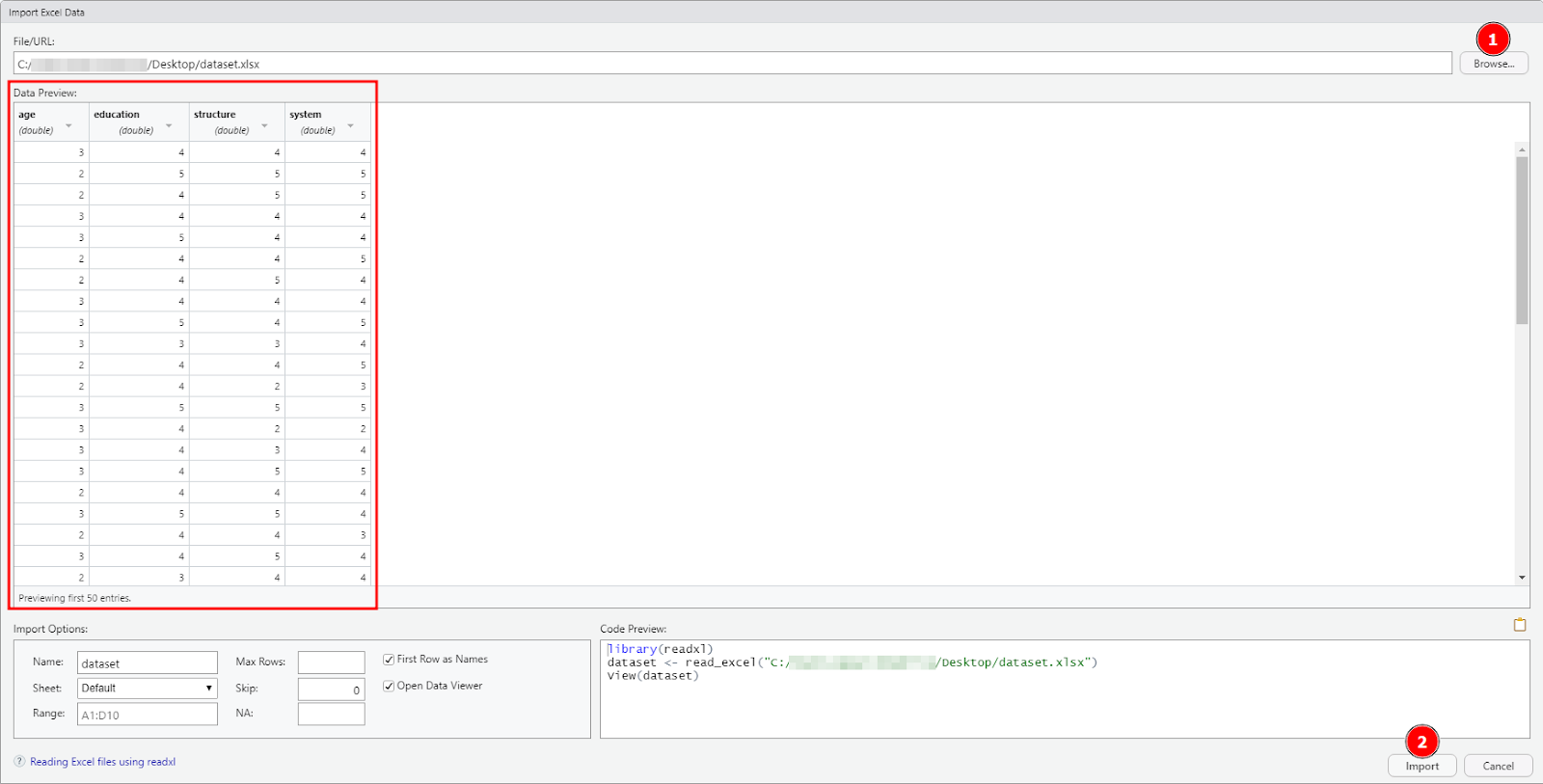
Fereastra RStudio Import Excel Data arătând butonul Browse pentru selectarea fișierului de date și butonul Import pentru încărcarea datelor

Fă clic pe Browse pentru a selecta fișierul Excel, apoi fă clic pe Import pentru a încărca setul de date în R.

NOTĂ: R ar putea necesita anumite biblioteci pentru a putea importa date din fișiere Excel (.xlsx, .csv, etc.). Dacă ești solicitat, permite RStudio să instaleze automat dependențele necesare.

(1) Găsește Eroarea Standard în R folosind Formula Erorii Standard

Primul pas este să traducem ecuația pentru eroarea standard a mediei într-o funcție nouă(x) în R. Să numim această funcție, de exemplu, stderr sau orice alt nume dorești.

Tastează această funcție în fereastra Console din R apoi apasă ENTER.

stderr <- function(x) sd(x)/sqrt(length(x))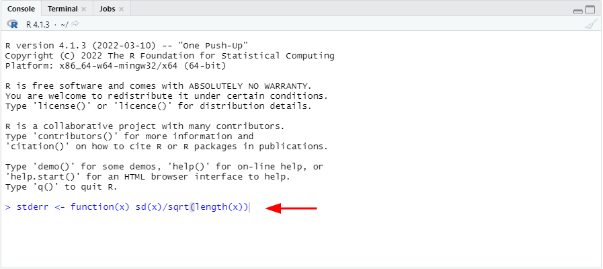

Consola RStudio arătând definiția funcției personalizate stderr pentru calcularea erorii standard folosind sd și sqrt în R

Creează o funcție personalizată stderr în Consola R: stderr <- function(x) sd(x)/sqrt(length(x)).

Apoi, să calculăm eroarea standard a mediei pentru coloana age din setul nostru de date.

Pentru a face acest lucru, vom invoca practic funcția pe care am creat-o și vom specifica fișierul setului de date și coloana pentru care dorim să calculăm abaterea standard în R folosind următoarea sintaxă:

stderr(dataset$age)

Unde:

stderr = funcție pentru formula erorii standard în R
dataset = fișierul setului de date pe care l-am importat în R
age = coloana (variabila) pentru care dorim să găsim valoarea erorii standard a mediei

Eroarea standard pentru variabila age din setul nostru de date este 0.06, așa cum se vede în captura de mai jos:

Ieșirea Consolei RStudio arătând rezultatul erorii standard de 0.06 după rularea funcției stderr pe variabila age

Funcția stderr(dataset$age) returnează o valoare a erorii standard de 0.06.

(2) Găsește Eroarea Standard în R folosind Biblioteca Plotrix

Această metodă folosește funcția std.error() din pachetul Plotrix în R. Mai întâi trebuie să instalăm biblioteca Plotrix tastând următoarea comandă în fereastra Console din R:

install.packages('plotrix')

Apoi, trebuie să apelăm biblioteca Plotrix în R folosind următoarea comandă:

library('plotrix')

În cele din urmă, putem folosi funcția std.error pentru a calcula eroarea standard a mediei pentru variabila system din setul nostru de date.

std.error(dataset$system)

Consola RStudio arătând funcția std.error din biblioteca Plotrix calculând eroarea standard pentru variabila system

Folosind funcția std.error() din Plotrix pentru a calcula eroarea standard pentru variabila system.

Întrebări Frecvente

Cum să găsești eroarea standard?

Pentru a găsi eroarea standard, împarte abaterea standard la rădăcina pătrată a dimensiunii eșantionului: SE = s / √n. În Excel, folosește =STDEV(interval)/SQRT(COUNT(interval)). În SPSS, folosește Analyze → Descriptive Statistics → Explore și verifică rândul Mean pentru Std. Error. În R, folosește `stderr <- function(x) sd(x)/sqrt(length(x))` apoi stderr(datele_tale).

Cum să calculezi eroarea standard în Excel?

Pentru a calcula eroarea standard în Excel: (1) Fă clic pe o celulă goală, (2) Introdu formula =STDEV(intervalul_tău)/SQRT(COUNT(intervalul_tău)), înlocuind 'intervalul_tău' cu intervalul real de celule (de ex., A1:A100), (3) Apasă ENTER. Excel va calcula eroarea standard a mediei pentru setul tău de date.

Cum să găsești eroarea standard în Excel?

Găsește eroarea standard în Excel folosind formula =STDEV(interval_date)/SQRT(COUNT(interval_date)). Aceasta împarte abaterea standard a datelor tale la rădăcina pătrată a dimensiunii eșantionului tău. De exemplu, dacă datele tale sunt în celulele A1 până la A50, folosește =STDEV(A1:A50)/SQRT(COUNT(A1:A50)).

Ce este eroarea standard a mediei?

Eroarea standard a mediei (SEM) măsoară cât de mult variază mediile eșantionului de la media adevărată a populației. Indică precizia mediei eșantionului tău ca estimare a mediei populației. O eroare standard mai mică înseamnă că eșantionul tău este mai reprezentativ pentru populație. Se calculează ca abaterea standard împărțită la rădăcina pătrată a dimensiunii eșantionului.

Cum să calculezi eroarea standard?

Calculează eroarea standard folosind formula: SE = s / √n, unde s este abaterea standard și n este dimensiunea eșantionului. Dacă cunoști abaterea standard a populației (σ), folosește SE = σ / √n. Eroarea standard scade pe măsură ce dimensiunea eșantionului crește, făcând estimarea ta mai precisă.

Cum să calculezi eroarea standard a mediei?

Pentru a calcula eroarea standard a mediei: (1) Calculează sau obține abaterea standard a eșantionului tău (s), (2) Numără dimensiunea eșantionului tău (n), (3) Calculează rădăcina pătrată a lui n, (4) Împarte s la √n. Formula este SE = s / √n. Pentru un eșantion cu abatere standard de 5 și n=100, SE = 5/√100 = 5/10 = 0.5.

Care este formula erorii standard?

Formula erorii standard este SE = s / √n pentru abaterea standard a eșantionului, sau SE = σ / √n pentru abaterea standard a populației. Unde SE este eroarea standard, s este abaterea standard a eșantionului, σ este abaterea standard a populației, și n este dimensiunea eșantionului. Această formulă arată că eroarea standard scade pe măsură ce dimensiunea eșantionului crește.

Cum să interpretezi eroarea standard?

Interpretează eroarea standard ca o măsură a preciziei eșantionării: Valori mai mici indică că mediile eșantionului sunt strâns grupate în jurul mediei populației (estimare mai precisă). Valori mai mari sugerează variabilitate mai mare între eșantioane (estimare mai puțin precisă). O eroare standard de 0.5 înseamnă că mediile eșantionului variază de obicei cu aproximativ 0.5 unități de la media adevărată a populației.

Eroare standard versus abatere standard?

Abaterea standard măsoară variabilitatea punctelor de date individuale din eșantionul tău. Eroarea standard măsoară cât de mult variază media eșantionului tău de la media adevărată a populației. Abaterea standard rămâne relativ constantă indiferent de dimensiunea eșantionului, în timp ce eroarea standard scade pe măsură ce dimensiunea eșantionului crește. SE = SD / √n arată această relație.

Ce este o eroare standard bună a mediei?

Nu există o valoare 'bună' universală a erorii standard - depinde de scala datelor tale și contextul cercetării. În general, mai mică este mai bună, deoarece indică mai multă precizie. Compară eroarea standard cu media ta: dacă SE este 1 și media este 100, aceasta este variabilitate de 1% (bună). Dacă SE este 10 și media este 20, aceasta este variabilitate de 50% (îngrijorătoare). Crește dimensiunea eșantionului pentru a reduce eroarea standard.

Concluzie

Eroarea standard a mediei măsoară diferența dintre mediile eșantionului comparate cu media populației adevărate. Cu alte cuvinte, ne spune dacă eșantionul nostru este reprezentativ pentru populația din care a fost luat.

Dacă analiza eșantionului arată o eroare standard ridicată, cea mai bună modalitate de a o reduce este prin creșterea dimensiunii eșantionului folosind colectarea aleatorie a datelor.

Subiecte Conexe: Dacă lucrezi cu date de sondaj sau chestionar, ar putea fi necesar să evaluezi fiabilitatea folosind Cronbach Alpha în Excel sau Cronbach Alpha în SPSS pentru a asigura că scalele tale de măsurare sunt consistente înainte de a calcula statistici descriptive precum eroarea standard.

Referințe

Field, A., Miles, J., & Field, Z. (2012). Discovering statistics using R. SAGE Publications.

Field, A. (2013). Discovering statistics using IBM SPSS statistics (4th ed.). SAGE Publications.

McNeil, E. (2020). Data management and visualization using R. – Songkhla: Epidemiology Unit, Faculty of Medicine, Prince of Songkla University, 2020.