Normality Test in R: Shapiro-Wilk, QQ Plots & Interpretation

•By Leonard Cucos•en
SPSS TutorialsStatistical TestsR Programming

Testing for normality in R is crucial before running parametric statistical analyses like t-tests, ANOVA, or linear regression. These tests assume your data follows a normal distribution, and violating this assumption can lead to invalid conclusions.

In this guide, we'll cover visual methods (histograms, QQ plots), statistical tests (Shapiro-Wilk, Kolmogorov-Smirnov, Anderson-Darling), and how to interpret normality test results in R.

What is Normality?

Normality refers to whether data follows a normal distribution. A normal distribution, also called a Gaussian distribution, is a bell-shaped curve characterized by its mean and standard deviation. The mean represents the center of the distribution, while the standard deviation represents the spread of the data around the mean.

Bell-shaped normal distribution curve showing characteristic symmetric shape with mean at center and data spread indicated by standard deviation Figure 1: Normal (Gaussian) distribution curve

The normal distribution is important because many parametric statistical tests (t-tests, ANOVA, linear regression) assume that the data being analyzed follows a normal distribution. If your data violates this normality assumption, these statistical tests may produce inaccurate results or invalid conclusions.

Visual Methods to Check Normality in R

Visual methods provide an intuitive way to assess whether your data follows a normal distribution. Here are the two most common visual approaches:

1. Histogram

A histogram is a graphical representation showing the frequency distribution of your data. If data follows a normal distribution, the histogram will display a symmetric, bell-shaped curve.

Here's how to create a histogram in R:

# Create sample data
data <- rnorm(100)

# Create histogram
hist(data, main = "Histogram of Sample Data",
     xlab = "Value", col = "lightblue")

This code generates 100 random numbers from a standard normal distribution (mean = 0, standard deviation = 1) using the rnorm() function and creates a histogram using the hist() function.

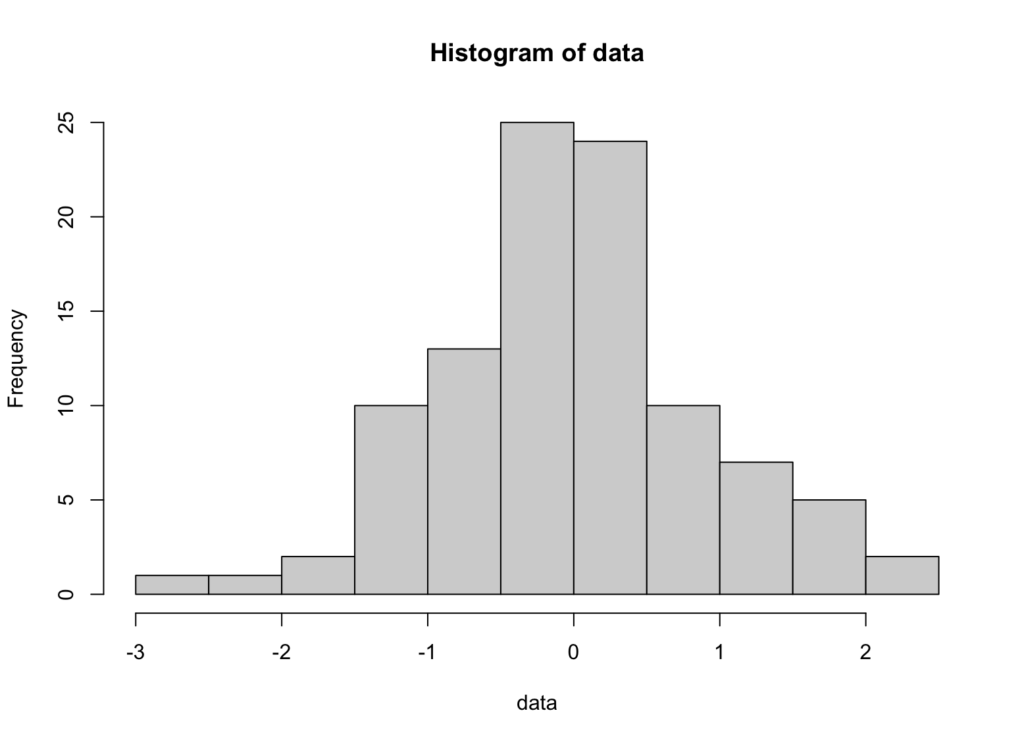Histogram showing bell-shaped distribution of 100 randomly generated data points from normal distribution with symmetric pattern Figure 2: Histogram showing normally distributed data

Interpretation: If the histogram shows a symmetric, bell-shaped curve centered around the mean, your data likely follows a normal distribution. Skewed or multimodal distributions indicate departures from normality.

2. QQ Plot (Quantile-Quantile Plot)

A QQ plot (quantile-quantile plot) compares the quantiles of your data against the quantiles of a theoretical normal distribution. It's one of the most reliable visual methods for assessing normality.

Here's how to create a QQ plot in R:

# Create sample data
data <- rnorm(100)

# Create QQ plot
qqnorm(data, main = "Normal Q-Q Plot")
qqline(data, col = "red")

This code generates 100 random numbers from a standard normal distribution and creates a QQ plot using the qqnorm() function. The qqline() function adds a reference line representing a perfect normal distribution.

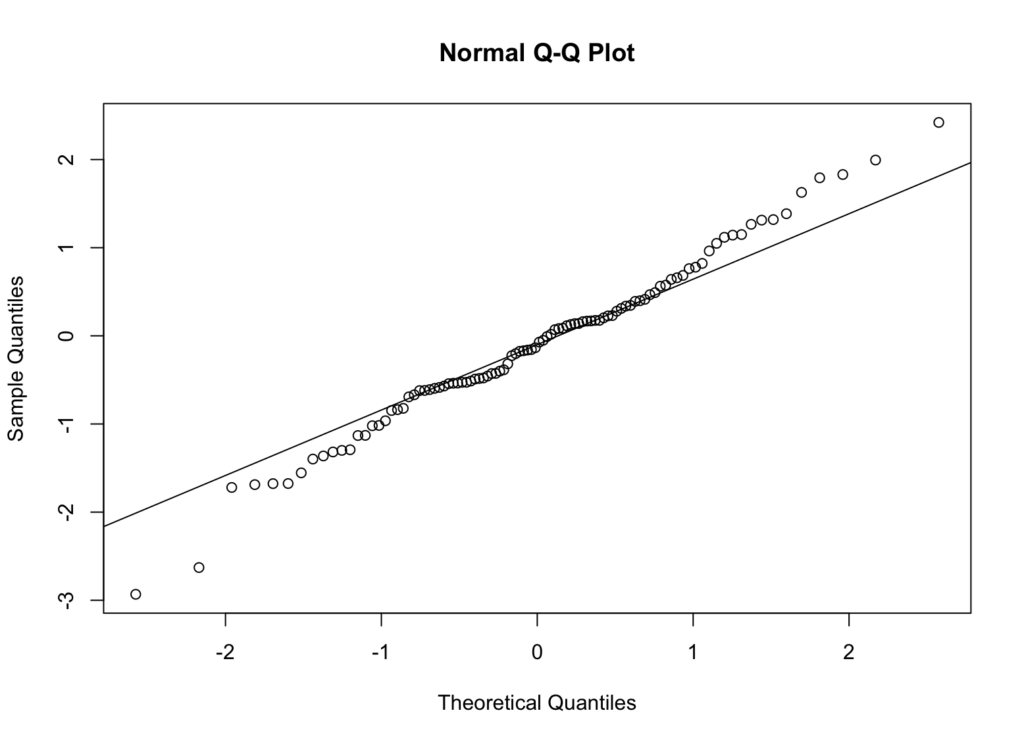QQ plot showing data points closely aligned with theoretical normal distribution reference line indicating normality Figure 3: QQ plot for normally distributed data

Interpretation: If your data follows a normal distribution, the points should fall approximately along the reference line. Systematic deviations from the line indicate non-normality:

  • Points curving above the line at the ends suggest heavy tails
  • Points curving below the line at the ends suggest light tails
  • S-shaped patterns indicate skewness

Statistical Tests for Normality in R

While visual methods are useful, statistical tests provide objective, quantitative assessments of normality. Here are the most common normality tests in R:

1. Shapiro-Wilk Test

The Shapiro-Wilk test is one of the most powerful normality tests, especially for small to medium sample sizes (n < 2000).

Hypotheses:

  • Null hypothesis (H₀): The data follows a normal distribution
  • Alternative hypothesis (H₁): The data does not follow a normal distribution

Here's how to perform the Shapiro-Wilk test in R:

# Create sample data
data <- rnorm(100)

# Perform Shapiro-Wilk test
shapiro.test(data)

This code generates 100 random numbers from a standard normal distribution and performs a Shapiro-Wilk test using the shapiro.test() function.

Shapiro-Wilk test output showing W statistic and p-value greater than 0.05 indicating normally distributed data Figure 4: Shapiro-Wilk test results

Interpretation:

  • p-value > 0.05: Fail to reject the null hypothesis; data appears normally distributed
  • p-value ≤ 0.05: Reject the null hypothesis; data significantly deviates from normality

Note: The Shapiro-Wilk test can be overly sensitive with large sample sizes, detecting trivial departures from normality that have little practical impact.

2. Kolmogorov-Smirnov Test

The Kolmogorov-Smirnov (K-S) test compares your data's cumulative distribution function against a theoretical normal distribution.

# Create sample data
data <- rnorm(100)

# Perform Kolmogorov-Smirnov test
ks.test(data, "pnorm", mean = mean(data), sd = sd(data))

Interpretation: Similar to the Shapiro-Wilk test, a p-value > 0.05 suggests the data follows a normal distribution.

Note: The K-S test is less powerful than the Shapiro-Wilk test for detecting departures from normality, especially in the tails of the distribution.

3. Anderson-Darling Test

The Anderson-Darling test places more weight on the tails of the distribution than the Kolmogorov-Smirnov test, making it more sensitive to deviations in the tails.

# Install and load package if needed
# install.packages("nortest")
library(nortest)

# Create sample data
data <- rnorm(100)

# Perform Anderson-Darling test
ad.test(data)

Interpretation: A p-value > 0.05 indicates the data is consistent with a normal distribution.

Choosing the Right Normality Test

Different normality tests have different strengths and are suited for different situations:

Shapiro-Wilk Test:

  • Best for small to medium sample sizes (n < 2000)
  • Most powerful normality test
  • Can be overly sensitive with large samples

Kolmogorov-Smirnov Test:

  • Suitable for any sample size
  • General-purpose test
  • Less powerful than Shapiro-Wilk

Anderson-Darling Test:

  • Good for detecting deviations in distribution tails
  • Works with any sample size
  • Requires the nortest package

Recommendation: For most applications with sample sizes under 2,000, use the Shapiro-Wilk test combined with QQ plots for visual confirmation.

Frequently Asked Questions

A normality test is a statistical procedure used to determine whether a dataset follows a normal (Gaussian) distribution. Common normality tests include the Shapiro-Wilk test, Kolmogorov-Smirnov test, and Anderson-Darling test. These tests are essential because many parametric statistical analyses (t-tests, ANOVA, regression) assume that data is normally distributed.
To test for normality in R, use a combination of visual and statistical methods: (1) Create a histogram with hist(data) to check for bell-shaped distribution, (2) Use QQ plots with qqnorm(data) and qqline(data) to see if points fall on the reference line, (3) Perform Shapiro-Wilk test with shapiro.test(data) - if p-value > 0.05, data is likely normal. For best results, use multiple methods together.
Interpret the Shapiro-Wilk test by examining the p-value: If p-value > 0.05, fail to reject the null hypothesis - your data appears normally distributed. If p-value ≤ 0.05, reject the null hypothesis - your data significantly deviates from normality. The W statistic ranges from 0 to 1, with values closer to 1 indicating better normality. Note that with very large samples, the test may detect trivial departures from normality.
Normality in statistics refers to whether data follows a normal distribution, characterized by a symmetric, bell-shaped curve. In a normal distribution, most observations cluster around the mean, with fewer observations in the tails. The distribution is fully described by two parameters: the mean (center) and standard deviation (spread). Normality is crucial because many statistical tests assume normally distributed data.
In normality tests, the p-value represents the probability of observing your data (or more extreme data) if it truly came from a normal distribution. A p-value > 0.05 suggests insufficient evidence to conclude the data is non-normal, so we treat it as normally distributed. A p-value ≤ 0.05 indicates significant evidence that the data does not follow a normal distribution, violating the normality assumption.
To check normality with a QQ plot, examine how closely the data points follow the reference line: If points fall approximately on the straight reference line, the data is likely normal. If points curve systematically above the line at the ends, the distribution has heavier tails than normal. If points curve below the line at the ends, the distribution has lighter tails. S-shaped patterns indicate skewness. Use qqnorm(data) and qqline(data) in R to create QQ plots.
The Shapiro-Wilk test in R is a statistical test for normality performed using the shapiro.test() function. It's one of the most powerful normality tests, especially for small to medium sample sizes (n < 2000). The test calculates a W statistic and p-value to determine if data significantly deviates from normality. Use it as: shapiro.test(your_data). It's the preferred normality test for most applications in R.
Use normality tests before conducting parametric statistical analyses that assume normal distributions, including t-tests, ANOVA, linear regression, and Pearson correlation. Test normality when checking assumptions for your analysis, when deciding between parametric and non-parametric tests, and when your sample size is too small for the Central Limit Theorem to apply (typically n < 30). Always combine statistical tests with visual inspection using histograms and QQ plots.

Wrapping Up

Testing for normality in R is a fundamental skill for data analysts and statisticians. This guide covered both visual methods (histograms and QQ plots) and statistical tests (Shapiro-Wilk, Kolmogorov-Smirnov, and Anderson-Darling) to assess whether your data follows a normal distribution.

Remember to use a combination of approaches: start with visual inspection using histograms and QQ plots, then confirm with statistical tests like the Shapiro-Wilk test. Understanding normality is essential before conducting parametric statistical analyses, as violations of the normality assumption can lead to incorrect conclusions.

For most applications with sample sizes under 2,000, the Shapiro-Wilk test combined with QQ plot visualization provides the most reliable assessment of normality in R.