Test de Normalitate în R: Shapiro-Wilk, Grafice QQ & Interpretare

Testarea normalității în R este crucială înainte de a rula analize statistice parametrice precum testele t, ANOVA sau regresia liniară. Testul Shapiro-Wilk, graficul QQ (quantile-quantile plot) și histogramele sunt cele mai comune metode pentru verificarea asumpției de normalitate a datelor. Aceste teste presupun că datele tale urmează o distribuție normală (Gaussiană), iar violarea acestei asumpții poate duce la concluzii invalide în analiza statistică.

În acest ghid, vom acoperi metodele vizuale (histograme, grafice QQ), testele statistice (Shapiro-Wilk, Kolmogorov-Smirnov, Anderson-Darling) și cum să interpretezi rezultatele testelor de normalitate în R.

Ce Este Normalitatea?

Normalitatea se referă la faptul dacă datele urmează o distribuție normală. O distribuție normală, numită și distribuție Gaussiană, este o curbă în formă de clopot caracterizată de media și deviația standard. Media reprezintă centrul distribuției, în timp ce deviația standard reprezintă răspândirea datelor în jurul mediei.

Curbă de distribuție normală în formă de clopot arătând forma simetrică caracteristică cu media în centru și răspândirea datelor indicată de deviația standard

Figura 1: Curba distribuției normale (Gaussiene)

Distribuția normală este importantă deoarece multe teste statistice parametrice (teste t, ANOVA, regresie liniară) presupun că datele analizate urmează o distribuție normală. Dacă datele tale violează această asumpție de normalitate, aceste teste statistice pot produce rezultate inexacte sau concluzii invalide.

Metode Vizuale pentru Verificarea Normalității în R

Metodele vizuale oferă o modalitate intuitivă de a evalua dacă datele tale urmează o distribuție normală. Iată cele două abordări vizuale cele mai comune:

1. Histograma

O histogramă este o reprezentare grafică care arată distribuția de frecvență a datelor tale. Dacă datele urmează o distribuție normală, histograma va afișa o curbă simetrică, în formă de clopot.

Iată cum să creezi o histogramă în R:

# Creează date exemplu
data <- rnorm(100)
 
# Creează histograma
hist(data, main = "Histograma Datelor Exemplu",
     xlab = "Valoare", col = "lightblue")

Acest cod generează 100 de numere aleatorii dintr-o distribuție normală standard (media = 0, deviația standard = 1) folosind funcția rnorm() și creează o histogramă folosind funcția hist().

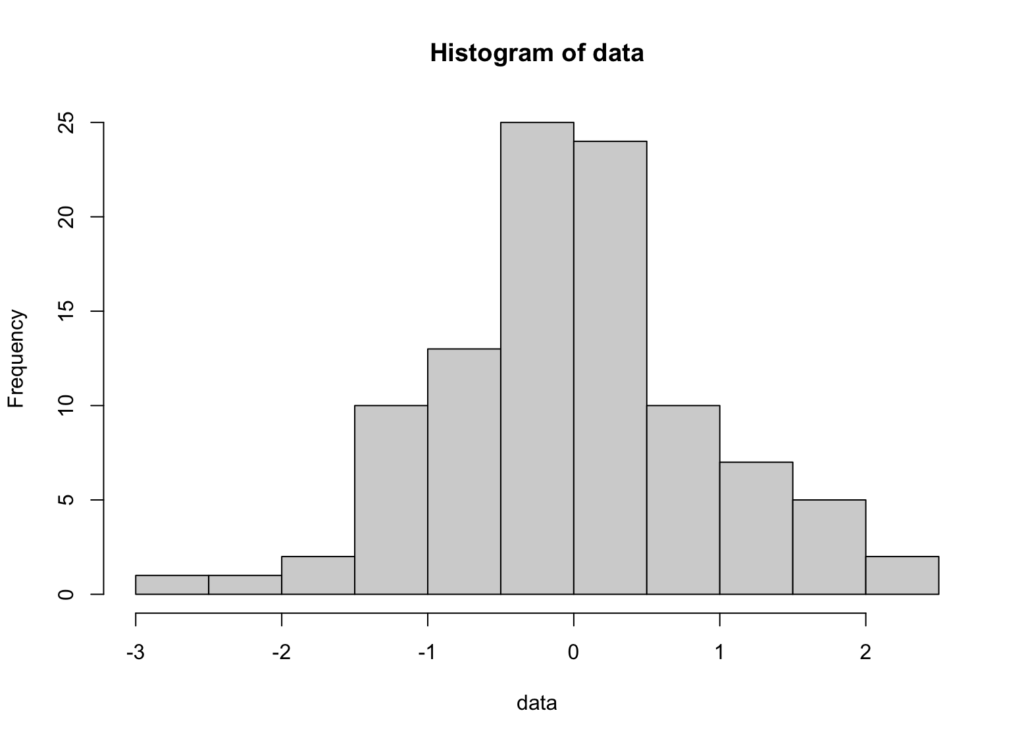
Histogramă arătând distribuția în formă de clopot a 100 de puncte de date generate aleator din distribuția normală cu tipar simetric

Figura 2: Histogramă arătând date distribuite normal

Interpretare: Dacă histograma arată o curbă simetrică, în formă de clopot, centrată în jurul mediei, datele tale probabil urmează o distribuție normală. Distribuțiile asimetrice sau multimodale indică abateri de la normalitate.

2. Grafic QQ (Quantile-Quantile Plot)

Un grafic QQ (quantile-quantile plot) compară cuantilele datelor tale cu cuantilele unei distribuții normale teoretice. Este una dintre cele mai fiabile metode vizuale pentru evaluarea normalității.

Iată cum să creezi un grafic QQ în R:

# Creează date exemplu
data <- rnorm(100)
 
# Creează grafic QQ
qqnorm(data, main = "Grafic Q-Q Normal")
qqline(data, col = "red")

Acest cod generează 100 de numere aleatorii dintr-o distribuție normală standard și creează un grafic QQ folosind funcția qqnorm(). Funcția qqline() adaugă o linie de referință reprezentând o distribuție normală perfectă.

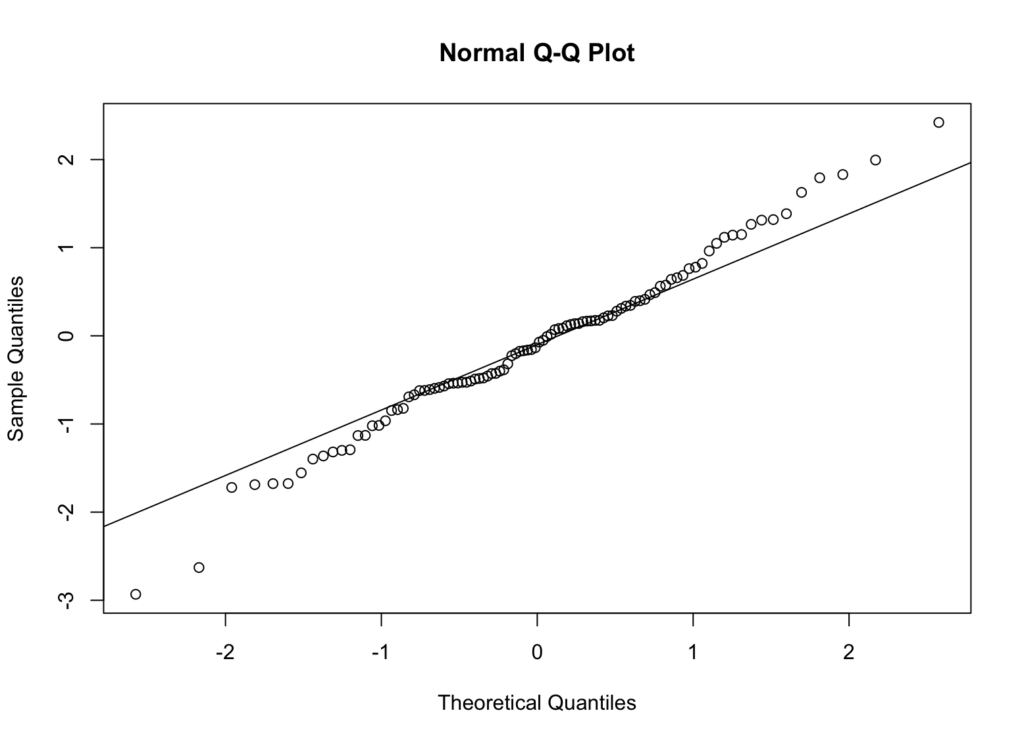
Grafic QQ arătând puncte de date strâns aliniate cu linia de referință a distribuției normale teoretice indicând normalitate

Figura 3: Grafic QQ pentru date distribuite normal

Interpretare: Dacă datele tale urmează o distribuție normală, punctele ar trebui să cadă aproximativ de-a lungul liniei de referință. Abaterile sistematice de la linie indică non-normalitate:

Puncte curbate deasupra liniei la capete sugerează cozi grele
Puncte curbate sub linie la capete sugerează cozi ușoare
Tiparele în formă de S indică asimetrie

Teste Statistice pentru Normalitate în R

Deși metodele vizuale sunt utile, testele statistice oferă evaluări obiective, cantitative ale normalității. Iată cele mai comune teste de normalitate în R:

1. Testul Shapiro-Wilk

Testul Shapiro-Wilk este unul dintre cele mai puternice teste de normalitate, în special pentru dimensiuni mici și medii ale eșantionului (n < 2000).

Ipoteze:

Ipoteza nulă (H₀): Datele urmează o distribuție normală
Ipoteza alternativă (H₁): Datele nu urmează o distribuție normală

Iată cum să efectuezi testul Shapiro-Wilk în R:

# Creează date exemplu
data <- rnorm(100)
 
# Efectuează testul Shapiro-Wilk
shapiro.test(data)

Acest cod generează 100 de numere aleatorii dintr-o distribuție normală standard și efectuează un test Shapiro-Wilk folosind funcția shapiro.test().

Rezultatul testului Shapiro-Wilk arătând statistica W și valoarea p mai mare de 0.05 indicând date distribuite normal

Figura 4: Rezultatele testului Shapiro-Wilk

Interpretare:

valoarea p > 0.05: Nu respingem ipoteza nulă; datele par distribuite normal
valoarea p ≤ 0.05: Respingem ipoteza nulă; datele deviază semnificativ de la normalitate

Notă: Testul Shapiro-Wilk poate fi excesiv de sensibil cu dimensiuni mari ale eșantionului, detectând abateri triviale de la normalitate care au impact practic redus.

2. Testul Kolmogorov-Smirnov

Testul Kolmogorov-Smirnov (K-S) compară funcția de distribuție cumulativă a datelor tale cu o distribuție normală teoretică.

# Creează date exemplu
data <- rnorm(100)
 
# Efectuează testul Kolmogorov-Smirnov
ks.test(data, "pnorm", mean = mean(data), sd = sd(data))

Interpretare: Similar cu testul Shapiro-Wilk, o valoare p > 0.05 sugerează că datele urmează o distribuție normală.

Notă: Testul K-S este mai puțin puternic decât testul Shapiro-Wilk pentru detectarea abaterilor de la normalitate, în special în cozile distribuției.

3. Testul Anderson-Darling

Testul Anderson-Darling pune mai multă greutate pe cozile distribuției decât testul Kolmogorov-Smirnov, făcându-l mai sensibil la abateri în cozi.

# Instalează și încarcă pachetul dacă este necesar
# install.packages("nortest")
library(nortest)
 
# Creează date exemplu
data <- rnorm(100)
 
# Efectuează testul Anderson-Darling
ad.test(data)

Interpretare: O valoare p > 0.05 indică că datele sunt consistente cu o distribuție normală.

Alegerea Testului de Normalitate Potrivit

Teste diferite de normalitate au puncte forte diferite și sunt potrivite pentru situații diferite:

Testul Shapiro-Wilk:

Cel mai bun pentru dimensiuni mici și medii ale eșantionului (n < 2000)
Cel mai puternic test de normalitate
Poate fi excesiv de sensibil cu eșantioane mari

Testul Kolmogorov-Smirnov:

Potrivit pentru orice dimensiune a eșantionului
Test cu scop general
Mai puțin puternic decât Shapiro-Wilk

Testul Anderson-Darling:

Bun pentru detectarea abaterilor în cozile distribuției
Funcționează cu orice dimensiune a eșantionului
Necesită pachetul nortest

Recomandare: Pentru majoritatea aplicațiilor cu dimensiuni ale eșantionului sub 2,000, folosește testul Shapiro-Wilk combinat cu grafice QQ pentru confirmare vizuală.

Întrebări Frecvente

Ce este testul de normalitate?

Un test de normalitate este o procedură statistică folosită pentru a determina dacă un set de date urmează o distribuție normală (Gaussiană). Testele comune de normalitate includ testul Shapiro-Wilk, testul Kolmogorov-Smirnov și testul Anderson-Darling. Aceste teste sunt esențiale deoarece multe analize statistice parametrice (teste t, ANOVA, regresie) presupun că datele sunt distribuite normal.

Cum să testez normalitatea în R?

Pentru a testa normalitatea în R, folosește o combinație de metode vizuale și statistice: (1) Creează o histogramă cu hist(data) pentru a verifica distribuția în formă de clopot, (2) Folosește grafice QQ cu qqnorm(data) și qqline(data) pentru a vedea dacă punctele cad pe linia de referință, (3) Efectuează testul Shapiro-Wilk cu shapiro.test(data) - dacă valoarea p > 0.05, datele sunt probabil normale. Pentru cele mai bune rezultate, folosește mai multe metode împreună.

Cum să interpretez testul Shapiro-Wilk?

Interpretează testul Shapiro-Wilk examinând valoarea p: Dacă valoarea p > 0.05, nu respingi ipoteza nulă - datele tale par distribuite normal. Dacă valoarea p ≤ 0.05, respingi ipoteza nulă - datele tale deviază semnificativ de la normalitate. Statistica W variază de la 0 la 1, cu valori mai aproape de 1 indicând normalitate mai bună. Notă că cu eșantioane foarte mari, testul poate detecta abateri triviale de la normalitate.

Ce este normalitatea în statistică?

Normalitatea în statistică se referă la faptul dacă datele urmează o distribuție normală, caracterizată de o curbă simetrică, în formă de clopot. Într-o distribuție normală, majoritatea observațiilor se grupează în jurul mediei, cu mai puține observații în cozi. Distribuția este descrisă complet de doi parametri: media (centrul) și deviația standard (răspândirea). Normalitatea este crucială deoarece multe teste statistice presupun date distribuite normal.

Ce înseamnă valoarea p în testul de normalitate?

În testele de normalitate, valoarea p reprezintă probabilitatea de a observa datele tale (sau date mai extreme) dacă ar proveni cu adevărat dintr-o distribuție normală. O valoare p > 0.05 sugerează dovezi insuficiente pentru a concluziona că datele sunt non-normale, deci le tratăm ca fiind distribuite normal. O valoare p ≤ 0.05 indică dovezi semnificative că datele nu urmează o distribuție normală, violând asumpția de normalitate.

Cum să verific normalitatea cu graficul QQ?

Pentru a verifica normalitatea cu un grafic QQ, examinează cât de aproape urmează punctele de date linia de referință: Dacă punctele cad aproximativ pe linia dreaptă de referință, datele sunt probabil normale. Dacă punctele se curbează sistematic deasupra liniei la capete, distribuția are cozi mai grele decât normalul. Dacă punctele se curbează sub linie la capete, distribuția are cozi mai ușoare. Tiparele în formă de S indică asimetrie. Folosește qqnorm(data) și qqline(data) în R pentru a crea grafice QQ.

Ce este testul Shapiro-Wilk în R?

Testul Shapiro-Wilk în R este un test statistic pentru normalitate efectuat folosind funcția shapiro.test(). Este unul dintre cele mai puternice teste de normalitate, în special pentru dimensiuni mici și medii ale eșantionului (n < 2000). Testul calculează o statistică W și o valoare p pentru a determina dacă datele deviază semnificativ de la normalitate. Folosește-l astfel: shapiro.test(datele_tale). Este testul de normalitate preferat pentru majoritatea aplicațiilor în R.

Când ar trebui să folosesc teste de normalitate?

Folosește teste de normalitate înainte de a efectua analize statistice parametrice care presupun distribuții normale, inclusiv teste t, ANOVA, regresie liniară și corelația Pearson. Testează normalitatea când verifici asumpțiile pentru analiza ta, când decizi între teste parametrice și non-parametrice, și când dimensiunea eșantionului tău este prea mică pentru ca Teorema Limită Centrală să se aplice (de obicei n < 30). Combină întotdeauna testele statistice cu inspecția vizuală folosind histograme și grafice QQ.

Concluzie

Testarea normalității în R este o abilitate fundamentală pentru analiștii de date și statisticieni. Acest ghid a acoperit atât metodele vizuale (histograme și grafice QQ), cât și testele statistice (Shapiro-Wilk, Kolmogorov-Smirnov și Anderson-Darling) pentru a evalua dacă datele tale urmează o distribuție normală.

Amintește-ți să folosești o combinație de abordări: începe cu inspecția vizuală folosind histograme și grafice QQ, apoi confirmă cu teste statistice precum testul Shapiro-Wilk. Înțelegerea normalității este esențială înainte de a efectua analize statistice parametrice, deoarece violările asumpției de normalitate pot duce la concluzii incorecte.

Pentru majoritatea aplicațiilor cu dimensiuni ale eșantionului sub 2,000, testul Shapiro-Wilk combinat cu vizualizarea graficului QQ oferă cea mai fiabilă evaluare a normalității în R.