Homoscedasticitatea este o asumpție fundamentală în regresia liniară și modelarea statistică. Înțelegerea a ce înseamnă homoscedasticitatea (varianța constantă a reziduurilor) este esențială pentru producerea unor rezultate statistice valide și fiabile.
Acest ghid explică asumpția de homoscedasticitate în statistică, cum să recunoști încălcările (heteroscedasticitatea) și soluții practice. Vei învăța diferența cheie între homoscedasticitate vs heteroscedasticitate și de ce încălcarea acestei asumpții duce la teste de ipoteze și intervale de încredere nefiabile în analiza de regresie.
Ce Este Asumpția de Homoscedasticitate?
Homoscedasticitatea (pronunțată "homo-sked-asti-ci-ta-te") descrie varianța constantă a reziduurilor sau erorilor pe toate nivelurile variabilelor independente dintr-un set de date.
Definiție: Într-un set de date homoscedastic, dispersia punctelor de date rămâne consistentă indiferent de valorile variabilei predictoare. Varianța nu se schimbă pe măsură ce variabila independentă se schimbă.
Exemplu: Într-un test de clasă, dacă variabilitatea scorurilor este similară pentru toate nivelurile de abilitate, aceasta este homoscedasticitate. Toți studenții prezintă o dispersie similară a scorurilor indiferent de nivelul lor de competență.
Heteroscedasticitatea (opusul) apare când varianța se schimbă pe nivelurile variabilei independente. În exemplul testului, varianța ar putea fi mai mare pentru studenții avansați și mai mică pentru începători. Dispersia nu este constantă.
Homoscedasticitatea și Regresia Liniară
Homoscedasticitatea este o asumpție critică în regresia liniară din mai multe motive:
-
Eficiența estimatorilor: Când homoscedasticitatea este respectată, metoda celor mai mici pătrate ordinare (OLS) furnizează cel mai bun estimator liniar nedeplasat (BLUE) cu varianța cea mai mică. Heteroscedasticitatea face estimatorii OLS ineficienți.
-
Validitatea testelor de ipoteze: Testele de ipoteze (teste t, teste F) presupun homoscedasticitate. Încălcările duc la statistici de test și valori p nefiabile, cauzând concluzii incorecte despre semnificația coeficienților.
-
Intervale de încredere: Datele homoscedastice produc intervale de încredere precise. Heteroscedasticitatea creează intervale prea largi sau prea înguste, ducând la inferențe incorecte.
-
Acuratețea predictivă: Cu varianță constantă, predicțiile modelului sunt în mod consistent fiabile pe toate nivelurile predictorilor. Heteroscedasticitatea compromite acuratețea predictivă pe măsură ce variabilitatea reziduală se schimbă.
Recunoașterea Homoscedasticității (și Heteroscedasticității)
Acum că am acoperit ce este homoscedasticitatea și de ce este importantă, să discutăm cum să o recunoști în datele tale. Există câteva modalități diferite de a verifica homoscedasticitatea, inclusiv metode grafice și teste statistice.
Metode Grafice
Creează un scatterplot al reziduurilor față de valorile prezise. În datele homoscedastice, punctele ar trebui să fie dispersate uniform fără modele sau grupări vizibile.
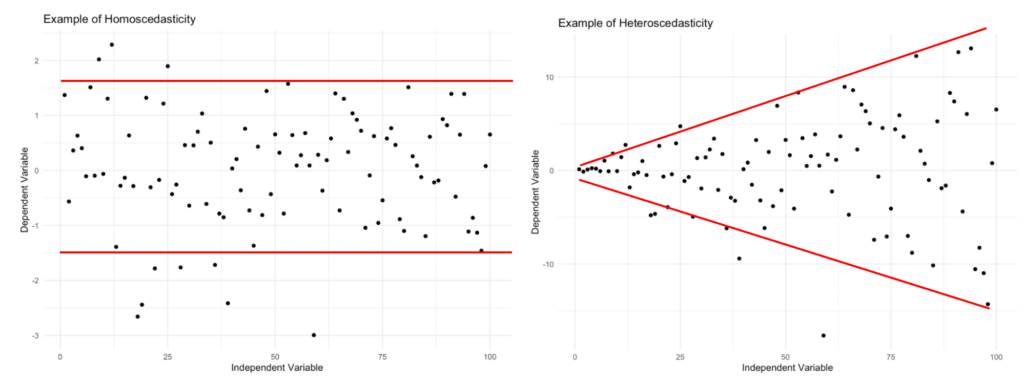
Homoscedasticitate vs. heteroscedasticitate: varianță constantă (stânga) versus varianță variabilă (dreapta)
Teste Statistice
Dacă preferi o abordare mai formală, există mai multe teste statistice disponibile pentru a verifica homoscedasticitatea. Câteva teste populare includ:
-
Testul Bartlett: Verifică varianțe egale în multiple grupuri. Rezultate semnificative indică heteroscedasticitate.
-
Testul Levene: Similar cu testul Bartlett, testul Levene verifică varianțe egale între grupuri. Mai puțin sensibil la non-normalitate, făcându-l mai robust.
-
Testul Breusch-Pagan: Utilizat în analiza de regresie. Testează dacă reziduurile pătratice se corelează cu variabilele independente. Rezultate semnificative indică heteroscedasticitate.
-
Testul White: Test mai general pentru heteroscedasticitate în regresie. Examinează dacă reziduurile pătratice se corelează cu combinații liniare sau pătratice ale variabilelor independente.
Pentru implementare practică, consultă ghidul nostru despre cum să testezi homoscedasticitatea în R cu atât metode grafice, cât și statistice (testul Breusch-Pagan).
Ține cont că niciun test nu este perfect și fiecare are limitările sale. În unele cazuri, poate fi util să folosești mai multe teste sau să le combini cu metode grafice pentru a obține o evaluare mai precisă a homoscedasticității.
Abordarea Heteroscedasticității
Dacă descoperi că datele tale sunt heteroscedastice, există mai multe strategii pentru a aborda această problemă:
-
Transformare: Transformă variabilele (logaritm, rădăcină pătrată, reciprocă) pentru a stabiliza varianța. Reține că transformarea schimbă interpretarea rezultatelor.
-
Regresia Ponderată: Acordă mai multă pondere observațiilor cu varianțe mai mici, mai puțină pondere varianțelor mai mari. Stabilizează varianța pe gamele de predictori.
-
Regresia Robustă: Folosește metode mai puțin sensibile la valori extreme și încălcări ale asumpțiilor. Furnizează estimări mai precise cu date heteroscedastice.
-
Bootstrapping: Tehnică de reeșantionare care furnizează estimări precise ale parametrilor populației chiar și cu heteroscedasticitate.
Homoscedasticitate vs. Heteroscedasticitate: Diferențe Cheie
| Aspect | Homoscedasticitate | Heteroscedasticitate |
|---|---|---|
| Varianță | Constantă pe toate nivelurile predictorilor | Se schimbă pe nivelurile predictorilor |
| Model vizual | Dispersie aleatoare, fără modele | Formă de pâlnie sau evantai |
| Eficiența OLS | BLUE (Cel Mai Bun Estimator Liniar Nedeplasat) | Ineficient, erori standard mai mari |
| Teste de ipoteze | Valori p și intervale de încredere valide | Valori p nefiabile, inferențe incorecte |
| Impact | Rezultate de încredere | Erori standard deplasate, teste înșelătoare |
Întrebări Frecvente
Concluzie
Homoscedasticitatea (varianța constantă a reziduurilor) este o asumpție critică în regresia liniară și multe teste statistice. Încălcarea acestei asumpții duce la erori standard nefiabile, teste de ipoteze invalide și intervale de încredere incorecte.
Puncte cheie:
- Ce este homoscedasticitatea: Varianță constantă pe toate nivelurile predictorilor
- Cum să verifici: Grafice vizuale (dispersie reziduală) și teste statistice (Breusch-Pagan, Levene, White)
- Soluții: Transformarea datelor, regresia ponderată, metode robuste, bootstrapping
- Impact: Asigură rezultate statistice valide și de încredere
Pentru implementare practică, consultă cum să testezi homoscedasticitatea în R cu exemple practice.