Linear Regression คืออะไร? วิธีการวิเคราะห์ Linear Regression ใน SPSS [พร้อมตัวอย่าง]

•By Leonard Cucos•th
Statistical TestsSPSS Tutorials

Linear Regression เป็นเทคนิคทางสถิติพื้นฐานที่สำคัญที่สุดในการวิเคราะห์ความสัมพันธ์ระหว่างตัวแปร บทความนี้จะอธิบาย Linear Regression คืออะไร และสอนวิธีการวิเคราะห์ Linear Regression ใน SPSS ทีละขั้นตอนพร้อมตัวอย่างข้อมูล

คุณจะได้เรียนรู้วิธีการรัน Linear Regression ใน SPSS วิธีการอ่านค่าและแปลผล R Square, ANOVA และ Coefficients รวมถึงวิธีการสร้างสมการ Regression เพื่อทำนายผลลัพธ์

Linear Regression คืออะไร?

Linear Regression (การถดถอยเชิงเส้น) คือวิธีการทางสถิติที่ใช้ในการศึกษาความสัมพันธ์ระหว่างตัวแปร โดยใช้เส้นตรง (Regression Line หรือ Least Squares Line) เพื่อแสดงให้เห็นว่าตัวแปรอิสระ (Independent Variable) หนึ่งตัวหรือมากกว่าส่งผลต่อตัวแปรตาม (Dependent Variable) อย่างไร

Linear Regression เป็นหนึ่งในเทคนิคการสร้างแบบจำลองเพื่อทำนายผลลัพธ์ (Predictive Modeling) ที่ได้รับความนิยมมากที่สุดในงานวิจัยและการวิเคราะห์ข้อมูล ทำให้เป็นทักษะที่จำเป็นสำหรับนักศึกษา นักวิจัย และนักวิเคราะห์ข้อมูล

ดังที่ชื่อบอกไว้ Linear Regression ใช้เส้นตรง (เรียกว่า Regression Line) เพื่อวัดความสัมพันธ์ระหว่างตัวแปร คิดถึงความสัมพันธ์นี้เป็นสาเหตุ (ตัวแปรอิสระ) และผลลัพธ์ (ตัวแปรตาม) โดย Linear Regression จะสร้างเส้นตรงเพื่อแสดงผลลัพธ์ที่คาดการณ์

ในสถิติ ตัวแปรอิสระมักถูกเรียกว่า Predictor หรือ Explanatory Variable ส่วนตัวแปรตามบางครั้งเรียกว่า Predicted Variable หรือ Outcome Variable

Linear Regression มีกี่ประเภท?

Linear Regression มีสองประเภท:

  • Simple Linear Regression - ใช้ตัวแปรอิสระ 1 ตัวในการทำนายผลลัพธ์
  • Multiple Linear Regression - ใช้ตัวแปรอิสระ 2 ตัวขึ้นไป

บทความนี้มุ่งเน้นที่ Simple Linear Regression ในงานวิจัย ความสัมพันธ์ในการทำนายมักถูกกำหนดผ่านสมมติฐาน เช่น การศึกษาผลกระทบของการโฆษณาที่มีต่อรายได้

วิธีการนำเข้าข้อมูลใน SPSS

เนื่องจากนี่เป็นบทความสอนแบบ Hands-on สำหรับการวิเคราะห์ Linear Regression ใน SPSS เราจะต้องมีข้อมูลเพื่อสร้าง Regression Line

ดาวน์โหลดชุดข้อมูลตัวอย่างด้านล่างเพื่อทำตามบทความนี้

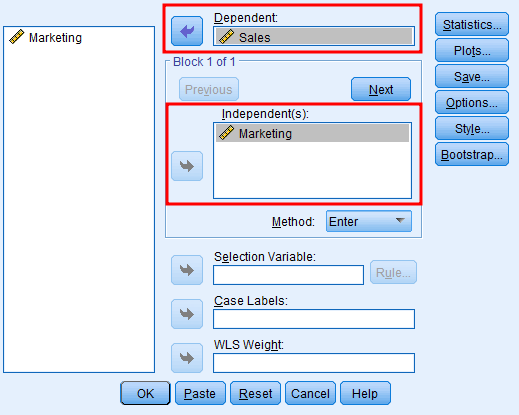
สมมติว่าเราต้องการศึกษาผลกระทบของการโฆษณา (Advertising) ที่มีต่อยอดขาย (Sales) ของบริษัทในบริบทของการวิจัย นี่คือลักษณะของชุดข้อมูล Excel ตัวอย่างที่คุณดาวน์โหลดมา

เมื่อดาวน์โหลดชุดข้อมูล Excel แล้ว ให้เปิด SPSS Statistics และในเมนูด้านบน ไปที่ File → Import Data → Excel

เลือกไฟล์ Excel ตัวอย่างที่ดาวน์โหลดมา และคลิก Open จากนั้นคลิก OK เมื่อระบบแจ้งให้อ่านไฟล์ Excel เมื่อนำเข้าข้อมูลใน SPSS แล้ว มันจะมีลักษณะดังนี้:

ตอนนี้ มาเรียนรู้วิธีการวิเคราะห์ Linear Regression ใน SPSS กัน ในเมนูด้านบนของ SPSS ไปที่ Analyze → Regression → Linear

เมนู SPSS แสดงการไปที่ Analyze → Regression → Linear 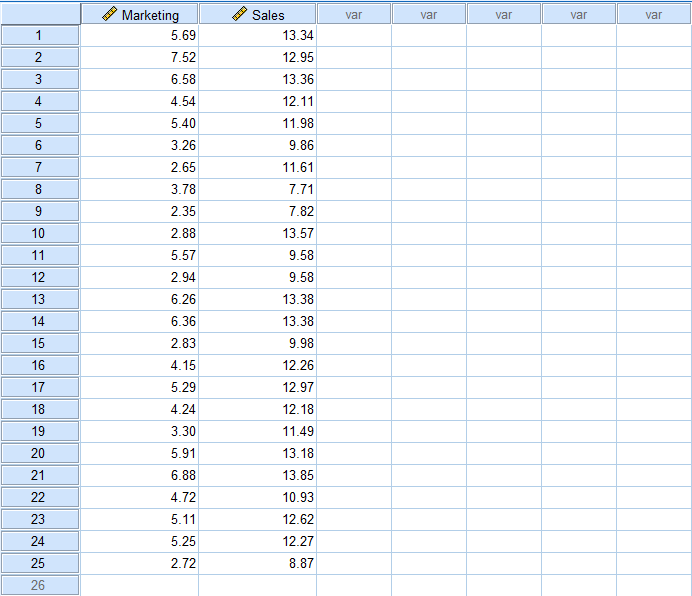การเข้าถึง Linear Regression ใน SPSS ผ่าน Analyze → Regression → Linear

ต่อไป เราต้องบอก SPSS ว่าตัวไหนคือตัวแปรอิสระและตัวแปรตามในชุดข้อมูล

โปรดจำไว้ว่า ใน Linear Regression เราศึกษาความสัมพันธ์เชิงสาเหตุระหว่างตัวแปรอิสระและตัวแปรตาม ในตัวอย่าง Excel ของเรา ตัวแปรอิสระคือ Marketing (สาเหตุ) และตัวแปรตามคือ Sales (ผลลัพธ์) กล่าวอีกนัยหนึ่ง เราต้องการทำนายว่าตัวแปร Sales ได้รับผลกระทบจากการเปลี่ยนแปลงของตัวแปร Marketing หรือไม่

ในหน้าต่าง Linear Regression เลือกตัวแปร Sales และคลิกปุ่มลูกศรถัดจากช่อง Dependent เพื่อเพิ่ม Sales เป็นตัวแปรตาม

หน้าต่าง Linear Regression ของ SPSS แสดงการเลือก Sales เป็นตัวแปรตาม 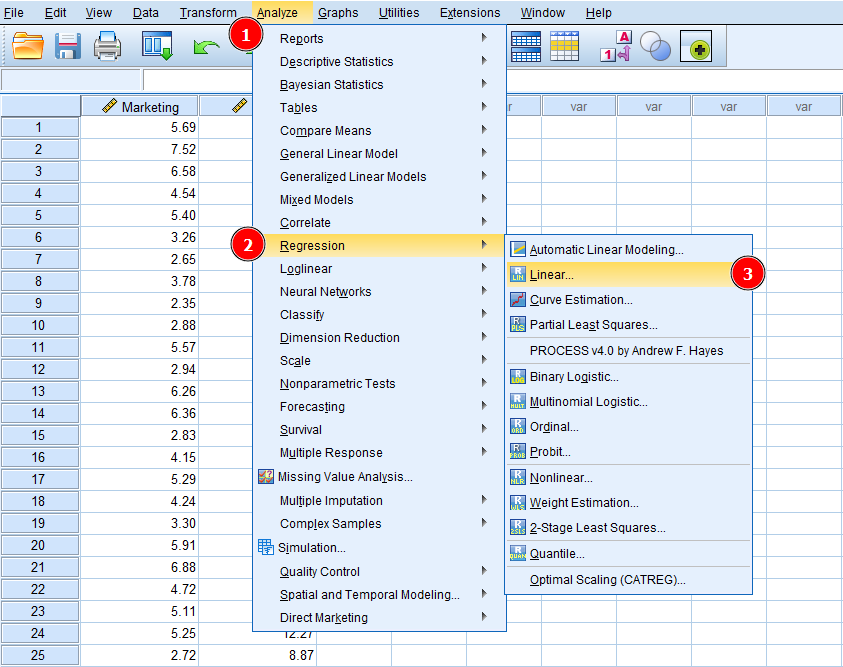การเพิ่มตัวแปรตาม (Sales) ใน Linear Regression ของ SPSS

ทำเช่นเดียวกันกับตัวแปร Marketing แต่คราวนี้ให้คลิกปุ่มลูกศรถัดจากช่อง Independent หน้าต่างการวิเคราะห์ควรมีลักษณะดังนี้:

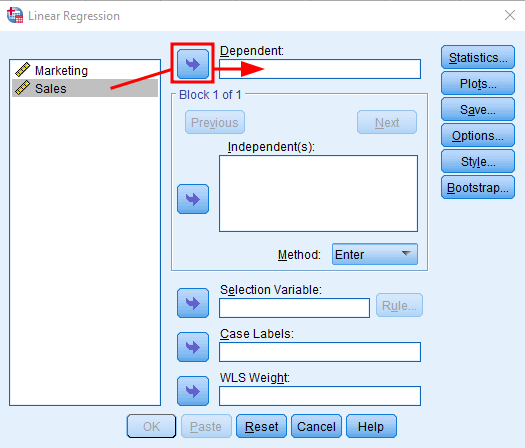หน้าต่าง Linear Regression ของ SPSS แสดง Marketing เป็นตัวแปรต้นและ Sales เป็นตัวแปรตาม การเพิ่มตัวแปรอิสระ (Marketing) ใน Linear Regression ของ SPSS

เราสามารถใช้ตัวเลือกอื่นๆ เพื่อปรับแต่งการวิเคราะห์เพิ่มเติม เช่น Method, Statistics, Plots, Style เป็นต้น แต่ในตัวอย่างนี้เราจะใช้การตั้งค่าเริ่มต้นซึ่งเพียงพอสำหรับกรณีนี้

คลิก OK เพื่อเริ่มการวิเคราะห์ และนี่คือลักษณะของผลลัพธ์การวิเคราะห์ Linear Regression ใน SPSS:

ผลลัพธ์ SPSS แสดงตาราง Model Summary, ANOVA และ Coefficients ของการวิเคราะห์ Linear Regression ผลลัพธ์ Linear Regression ใน SPSS แสดง Model Summary, ANOVA และ Coefficients

ผลลัพธ์แสดงตัวแปรอิสระและตัวแปรตามที่ใช้ในการวิเคราะห์นี้ Model Summary, ANOVA, Coefficients และค่าทางสถิติที่เกี่ยวข้อง มาทำความเข้าใจว่าผลลัพธ์การวิเคราะห์บอกอะไรเรา

การอ่านค่าและแปลผล Linear Regression

ส่วนนี้จะอธิบายความหมายของแต่ละค่าในผลลัพธ์ SPSS โดยเน้นที่ส่วนที่สำคัญที่สุดสำหรับการวิเคราะห์ของคุณ

  • ตาราง Variables Entered/Removed แสดงสรุปเชิงพรรณนาของการวิเคราะห์

  • Model 1 (Enter) หมายความว่าตัวแปรทั้งหมดที่ร้องขอถูกป้อนในขั้นตอนเดียวและได้รับความสำคัญเท่าเทียมกัน Enter Model เป็นที่นิยมใช้ในการวิเคราะห์ Regression จึงเป็นโมเดลเริ่มต้นใน SPSS

  • Variables Entered แสดงตัวแปรอิสระ (Marketing) ที่ใช้ในการวิเคราะห์ ไม่มีตัวแปรถูกลบออก ดังนั้นคอลัมน์ Variables Removed จึงว่างเปล่า

  • ใน SPSS ตัวแปรตาม (ในกรณีนี้คือ Sales) จะถูกระบุไว้ใต้ตารางพรรณนา

การอ่านค่า Model Summary

ตาราง Model Summary บอกสรุปผลลัพธ์ของการวิเคราะห์ใน SPSS

ตาราง Model Summary ของ SPSS แสดงค่า R, R Square, Adjusted R Square และ Standard Error ตาราง Model Summary จากผลลัพธ์ Linear Regression

  • R หมายถึงค่าสหสัมพันธ์ (Correlation) ระหว่างตัวแปร สหสัมพันธ์มีความสำคัญต่อการวิเคราะห์ Regression เพราะเราสามารถสันนิษฐานได้ว่าตัวแปรหนึ่งส่งผลต่ออีกตัวหนึ่งถ้าทั้งสองมีความสัมพันธ์กัน หากตัวแปรสองตัวไม่มีความสัมพันธ์กัน ก็อาจไม่มีประโยชน์ที่จะมองหาความสัมพันธ์เชิงสาเหตุ

สหสัมพันธ์ไม่ได้รับประกันความสัมพันธ์เชิงสาเหตุ แต่เป็นเงื่อนไขที่จำเป็นสำหรับความสัมพันธ์เชิงสาเหตุ

ค่า R มีช่วงตั้งแต่ -1 ถึง +1 โดย -1 คือความสัมพันธ์เชิงลบสมบูรณ์ +1 คือความสัมพันธ์เชิงบวกสมบูรณ์ และ 0 หมายถึงไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปร

ในกรณีของเรา R = 0.663 แสดงว่าตัวแปร Marketing และ Sales มีความสัมพันธ์กัน

  • R Square วัดอิทธิพลรวมของตัวแปรอิสระที่มีต่อตัวแปรตาม โปรดทราบว่าค่า R Square อธิบายเป็นเปอร์เซ็นต์ (%) ตัวอย่างเช่น ในตัวอย่างของเรา R Square = 0.440 ซึ่งหมายความว่า 44% ของ Sales ได้รับอิทธิพลจากกลยุทธ์ Marketing ของบริษัท

ค่า R Square ควรมีค่าเท่าไร? โดยทั่วไปค่า R Square ที่มากกว่า 0.50 (50%) ถือว่าดี แต่ขึ้นอยู่กับสาขาวิชาด้วย ในบางสาขา R Square 0.30-0.40 (30-40%) ก็ถือว่ายอมรับได้

  • Adjusted R Square เป็นค่าปรับที่ใช้ในกรณีที่โมเดลของคุณไม่กระชับ (Non-parsimonious) กล่าวง่ายๆ คือ หากกรอบแนวคิดการวิจัยของคุณมีตัวแปรที่ไม่จำเป็นในการทำนายผลลัพธ์ จะมีการลงโทษสะท้อนในค่า Adjusted R Square

ในตัวอย่างของเรา ความแตกต่างระหว่าง Adjusted R Square (0.416) และ R Square (0.440) คือ 0.024 ซึ่งไม่มีนัยสำคัญ

จำไว้ว่า เราควรมองหาคำอธิบายที่เรียบง่ายและไม่ซับซ้อนสำหรับปรากฏการณ์ที่กำลังศึกษา

  • Standard Error of the Estimate หมายถึงความแม่นยำของการทำนายรอบๆ Regression Line หากค่า Standard Error อยู่ระหว่าง -2 และ +2 แสดงว่า Regression Line ใกล้เคียงกับค่าจริง

ในกรณีของเรา Standard Error of the Estimate = 1.40 ซึ่งถือว่าดี

การอ่านค่า ANOVA

การทดสอบ ANOVA เป็นขั้นตอนเบื้องต้นของการวิเคราะห์ Linear Regression กล่าวอีกนัยหนึ่ง มันบอกเราว่าผลลัพธ์ที่ได้จากตัวอย่างสามารถสรุปเป็นภาพรวมของประชากรที่ตัวอย่างเป็นตัวแทนได้หรือไม่

โปรดจำไว้ว่า เพื่อให้การวิเคราะห์ Linear Regression ถูกต้อง ผลลัพธ์ ANOVA ต้องมีนัยสำคัญ (p < 0.05) นอกจากนี้ โมเดล Regression ควรเป็นไปตามสมมติฐานสำคัญ รวมถึง Homoscedasticity (ความแปรปรวนคงที่), Linearity และการแจกแจงปกติของ Residuals

ตาราง ANOVA ของ SPSS แสดงค่า Sum of Squares, df, Mean Square, F และค่านัยสำคัญ ตาราง ANOVA จากผลลัพธ์ Linear Regression

  • Sum of Squares วัดว่าจุดข้อมูลในชุดของคุณเบี่ยงเบนจาก Regression Line มากน้อยเพียงใด และช่วยให้คุณเข้าใจว่าโมเดล Regression แสดงข้อมูลได้ดีเพียงใด

กฎง่ายๆ สำหรับทั้ง Regression และ Residual Sum of Squares คือ ยิ่งค่าต่ำ ข้อมูลยิ่งแสดงโมเดลของคุณได้ดี

โปรดจำไว้ว่า Sum of Squares จะเป็นตัวเลขบวกเสมอ โดย 0 เป็นค่าต่ำสุดและแสดงถึงโมเดลที่เหมาะสมที่สุด

  • DF ใน ANOVA ย่อมาจาก Degree of Freedom (องศาอิสระ) กล่าวง่ายๆ DF แสดงจำนวนค่าอิสระที่ใช้ในการคำนวณค่าประมาณ

โปรดจำไว้ว่า ขนาดตัวอย่างที่เล็กกว่ามักหมายถึงองศาอิสระที่ต่ำกว่า (เช่นตัวอย่างของเรา) ในทางตรงกันข้าม ขนาดตัวอย่างที่ใหญ่กว่าจะมีองศาอิสระที่สูงกว่า ซึ่งมีประโยชน์ในการปฏิเสธสมมติฐานหลักที่เป็นเท็จและให้ผลลัพธ์ที่มีนัยสำคัญ

  • Mean Square ใน ANOVA ใช้เพื่อกำหนดนัยสำคัญของ Treatments (ปัจจัย ตามลำดับคือความแปรผันระหว่างค่าเฉลี่ยตัวอย่าง) Mean Square มีความสำคัญในการคำนวณค่า F Ratio

  • F Test ใน ANOVA ใช้เพื่อหาว่าค่าเฉลี่ยระหว่างสองประชากรแตกต่างกันอย่างมีนัยสำคัญหรือไม่ ค่า F ที่คำนวณจากข้อมูล (F=18.071) มักเรียกว่า F-statistics และมีประโยชน์เมื่อพิจารณาปฏิเสธสมมติฐานหลัก

  • Sig. ย่อมาจาก Significance (นัยสำคัญ) หากคุณไม่ต้องการลงลึกถึงรายละเอียดของการทดสอบ ANOVA นี่คือคอลัมน์ที่คุณควรดูก่อน ค่า Sig. < 0.05 ถือว่ามีนัยสำคัญ ในตัวอย่างของเรา Sig. = 0.000 ซึ่งน้อยกว่า 0.05 ดังนั้นจึงมีนัยสำคัญ

การอ่านค่า Coefficients

สุดท้าย เราพร้อมที่จะไปยังตารางผลลัพธ์การวิเคราะห์ Regression ใน SPSS

ในตาราง Coefficients มีเพียงหนึ่งค่าที่สำคัญที่สุดสำหรับการแปลผล: ค่า Sig. ซึ่งอยู่ในคอลัมน์สุดท้าย มาเริ่มต้นที่นั่นก่อน

ตาราง Coefficients ของ SPSS แสดงค่า B, Standard Error, Beta, t-value และค่านัยสำคัญ ตาราง Coefficients จากผลลัพธ์ Linear Regression

  • Sig. หรือที่เรียกว่า P-value แสดงระดับนัยสำคัญที่ตัวแปรอิสระมีต่อตัวแปรตาม คล้ายกับ ANOVA หากค่า Sig. < 0.05 แสดงว่ามีนัยสำคัญระหว่างตัวแปรใน Linear Regression

ในกรณีของเรา Sig. = 0.000 แสดงนัยสำคัญที่แข็งแกร่งระหว่างตัวแปรอิสระ (Marketing) และตัวแปรตาม (Sales)

  • Unstandardized B (Beta) โดยพื้นฐานแล้วแสดงความชัน (Slope) ของ Regression Line ระหว่างตัวแปรอิสระและตัวแปรตาม และบอกเราว่าเมื่อตัวแปรอิสระเพิ่มขึ้น 1 หน่วย ตัวแปรตามจะเพิ่มขึ้นเท่าไร

ในกรณีของเรา สำหรับทุกๆ หนึ่งหน่วยที่เพิ่มขึ้นใน Marketing, Sales จะเพิ่มขึ้น 0.808 หน่วย การเพิ่มขึ้นของหน่วยสามารถแสดงเป็นสกุลเงินได้

แถว Constant ในตาราง Coefficients แสดงค่าของตัวแปรตามเมื่อตัวแปรอิสระ = 0

ยิ่งค่า Standard Error สูง จุดข้อมูลบน Regression Line ยิ่งกระจายมากขึ้น ยิ่งจุดข้อมูลกระจาย โอกาสที่จะพบนัยสำคัญระหว่างตัวแปรก็น้อยลง

  • Standardized Coefficients Beta มีค่าตั้งแต่ -1 ถึง +1 โดย 0 หมายถึงไม่มีความสัมพันธ์ 0 ถึง -1 หมายถึงความสัมพันธ์เชิงลบ และ 0 ถึง +1 หมายถึงความสัมพันธ์เชิงบวก ยิ่งค่า Standardized Coefficient Beta ใกล้ -1 หรือ +1 ความสัมพันธ์ระหว่างตัวแปรยิ่งแข็งแกร่ง

ในกรณีของเรา Standardized Coefficient Beta = 0.663 แสดงความสัมพันธ์เชิงบวกระหว่างตัวแปรอิสระ (Marketing) และตัวแปรตาม (Sales)

  • t แสดงถึง t-test และใช้ในการคำนวณค่า p-value (Sig.) โดยทั่วไป t-test ใช้เพื่อเปรียบเทียบค่าเฉลี่ยของสองชุดข้อมูลและพิจารณาว่ามาจากประชากรเดียวกันหรือไม่

สมการ Regression

สมการ Regression มาจากตาราง Coefficients ใช้สูตร: Y = Constant + (B × X)

โดยที่:

  • Y = ตัวแปรตาม
  • B = Unstandardized Coefficient
  • X = ตัวแปรอิสระ

ตัวอย่างเช่น หาก Constant = 3.5 และ B = 0.808 สมการคือ: Sales = 3.5 + (0.808 × Marketing)

คำถามที่พบบ่อย

เพื่อรัน Linear Regression ใน SPSS: (1) นำเข้าข้อมูลผ่าน File → Import Data → Excel, (2) ไปที่ Analyze → Regression → Linear, (3) ย้ายตัวแปรตามไปที่ช่อง 'Dependent', (4) ย้ายตัวแปรอิสระไปที่ช่อง 'Independent(s)', (5) คลิก OK SPSS จะสร้างผลลัพธ์แสดง Model Summary, ANOVA และ Coefficients
เน้นที่สามส่วนหลัก: (1) R Square ใน Model Summary แสดงเปอร์เซ็นต์ความแปรปรวนที่ตัวแปรอิสระอธิบายได้ (เช่น 0.440 = 44%), (2) ค่า Sig. ในตาราง ANOVA ต้อง < 0.05 เพื่อให้มีนัยสำคัญ, (3) ค่า Sig. ในตาราง Coefficients แสดงว่าแต่ละ Predictor มีนัยสำคัญหรือไม่ ค่า Unstandardized B Coefficient บอกว่าตัวแปรตามเปลี่ยนแปลงเท่าไรต่อหนึ่งหน่วยที่เพิ่มขึ้นของตัวแปรอิสระ
R Square วัดเปอร์เซ็นต์ของความแปรปรวนในตัวแปรตามที่ถูกอธิบายโดยตัวแปรอิสระ ตัวอย่างเช่น R Square = 0.440 หมายความว่า 44% ของความแปรปรวนในตัวแปรตามถูกอธิบายโดยตัวแปรอิสระ ค่า R Square ที่สูงขึ้น (ใกล้ 1.0) บ่งชี้ว่าโมเดลเหมาะสมกับข้อมูลดีขึ้น
ตรวจสอบคอลัมน์ Sig. ในตาราง ANOVA - ต้อง < 0.05 เพื่อให้มีนัยสำคัญทางสถิติ ตรวจสอบคอลัมน์ Sig. ในตาราง Coefficients สำหรับแต่ละตัวแปร Predictor ด้วย หากทั้งสองค่า < 0.05 โมเดล Regression ของคุณมีนัยสำคัญและตัวแปรอิสระสามารถทำนายตัวแปรตามได้อย่างมีนัยสำคัญ
Simple Linear Regression ใช้ตัวแปรอิสระ 1 ตัวในการทำนายตัวแปรตาม (เช่น Marketing ทำนาย Sales หรือไม่?) Multiple Linear Regression ใช้ตัวแปรอิสระ 2 ตัวหรือมากกว่า (เช่น Marketing และ Price รวมกันทำนาย Sales หรือไม่?) ขั้นตอนใน SPSS เหมือนกัน - เพียงแค่เพิ่มตัวแปรหลายตัวในช่อง Independent(s) สำหรับ Multiple Regression

สรุป

อย่างที่คุณเห็น การเรียนรู้วิธีการวิเคราะห์ Linear Regression ใน SPSS ไม่ยาก แต่การทำความเข้าใจผลลัพธ์อาจท้าทายบ้าง โดยเฉพาะอย่างยิ่งถ้าคุณไม่รู้ว่าค่าใดมีความเกี่ยวข้องกับการวิเคราะห์ของคุณ

สิ่งสำคัญที่สุดที่ต้องจำไว้เมื่อประเมินผลลัพธ์การวิเคราะห์ Linear Regression คือต้องมองหานัยสำคัญทางสถิติ (Sig. < 0.05)

สำหรับเทคนิค Regression ขั้นสูง สามารถศึกษาการวิเคราะห์ตัวแปรกำกับใน SPSS เพื่อทดสอบผลกระทบปฏิสัมพันธ์ระหว่างตัวแปร หรือเรียนรู้เกี่ยวกับการวิเคราะห์ตัวแปรคั่นกลางใน SPSS สำหรับการวิเคราะห์ความสัมพันธ์แบบไม่ทางตรง