การวิเคราะห์ตัวแปรกำกับ (Moderation Analysis) ช่วยให้คุณเข้าใจว่า เมื่อใด ความสัมพันธ์ระหว่างสองตัวแปรเปลี่ยนแปลง แทนที่จะถามว่า X มีผลต่อ Y หรือไม่ การวิเคราะห์ตัวแปรกำกับจะถามว่า: "ความแข็งแกร่งของความสัมพันธ์ X→Y ขึ้นอยู่กับตัวแปรที่สาม (ตัวแปรกำกับ) หรือไม่?"
ในคู่มือนี้ คุณจะได้เรียนรู้สองวิธีปฏิบัติในการวิเคราะห์ตัวแปรกำกับใน SPSS: แนวทางด้วยตนเองพร้อมการทำให้เป็นมาตรฐาน และวิธี PROCESS Macro สมัยใหม่
ตัวแปรกำกับ คือ อะไร?
การวิเคราะห์ตัวแปรกำกับ (Moderation Analysis) ทดสอบว่าความสัมพันธ์ระหว่างตัวแปรอิสระ (X) และตัวแปรตาม (Y) เปลี่ยนแปลงขึ้นอยู่กับระดับของตัวแปรที่สามที่เรียกว่า ตัวแปรกำกับ (Moderator หรือ M) หรือไม่
คิดแบบนี้: ผลกระทบของ X ต่อ Y ไม่เหมือนกันสำหรับทุกคน มัน ขึ้นอยู่กับ M
ตัวอย่างคำถามวิจัย: "อายุ (M) กำกับความสัมพันธ์ระหว่างคุณภาพความสัมพันธ์ของลูกค้า (X) และความภักดีของผู้บริโภค (Y) หรือไม่?"
ในตัวอย่างนี้:
- ตัวแปรอิสระ (X): คุณภาพความสัมพันธ์ของลูกค้า
- ตัวแปรกำกับ (M): อายุ
- ตัวแปรตาม (Y): ความภักดีของผู้บริโภค
คำถามวิจัยถาม: ความสัมพันธ์ระหว่างคุณภาพความสัมพันธ์และความภักดี แข็งแกร่ง หรือ อ่อนแอ กว่าสำหรับลูกค้าที่อายุมากกว่าเทียบกับลูกค้าที่อายุน้อยกว่าหรือไม่?
ทำความเข้าใจความแตกต่างระหว่างตัวแปรกำกับและตัวแปรคั่นกลาง
ตัวแปรกำกับแตกต่างจากตัวแปรคั่นกลางโดยพื้นฐาน:
ตัวแปรกำกับ (Moderation): M เปลี่ยน ความแข็งแกร่ง หรือ ทิศทาง ของความสัมพันธ์ X→Y (ผลกระทบปฏิสัมพันธ์)
ตัวแปรคั่นกลาง (Mediation): M ส่งผ่าน ผลกระทบจาก X ไปยัง Y (ผลกระทบทางอ้อม)
ในตัวแปรกำกับ M ไม่ มีความสัมพันธ์เชิงสาเหตุกับ X ตัวแปรกำกับเป็นอิสระจากตัวทำนาย
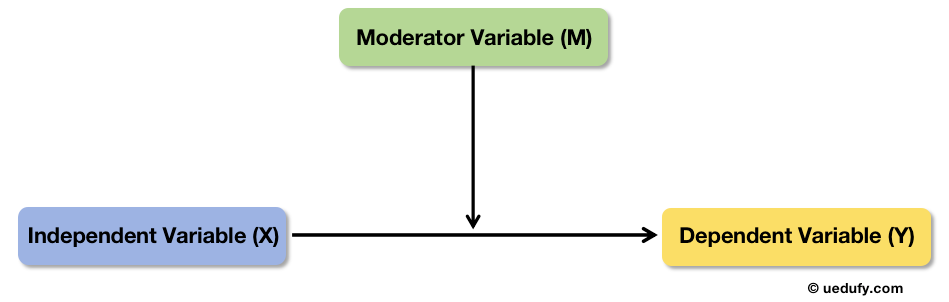 แผนภาพแนวคิดของตัวแปรกำกับแสดงให้เห็นว่า M มีอิทธิพลต่อความแข็งแกร่งของความสัมพันธ์ X→Y
แผนภาพแนวคิดของตัวแปรกำกับแสดงให้เห็นว่า M มีอิทธิพลต่อความแข็งแกร่งของความสัมพันธ์ X→Y
เทอมปฏิสัมพันธ์ (Interaction Term)
ตัวแปรกำกับถูกทดสอบโดยใช้ เทอมปฏิสัมพันธ์ (เรียกอีกอย่างว่า product term) คำนวณเป็น:
Interaction = X × M
เมื่อคุณรวมเทอมปฏิสัมพันธ์นี้ในโมเดลการถดถอย ผลกระทบปฏิสัมพันธ์ที่มีนัยสำคัญบ่งชี้การกำกับ
วิธีที่ 1: การวิเคราะห์ตัวแปรกำกับด้วยตนเอง
วิธีด้วยตนเองต้องการขั้นตอนมากกว่า แต่ช่วยให้คุณเข้าใจกลไกพื้นฐานของการวิเคราะห์ตัวแปรกำกับ แนวทางนี้เกี่ยวข้องกับการทำให้ตัวแปรเป็นมาตรฐาน การสร้างเทอมปฏิสัมพันธ์ และการรันการถดถอยเชิงเส้น
ชุดข้อมูลตัวอย่าง:
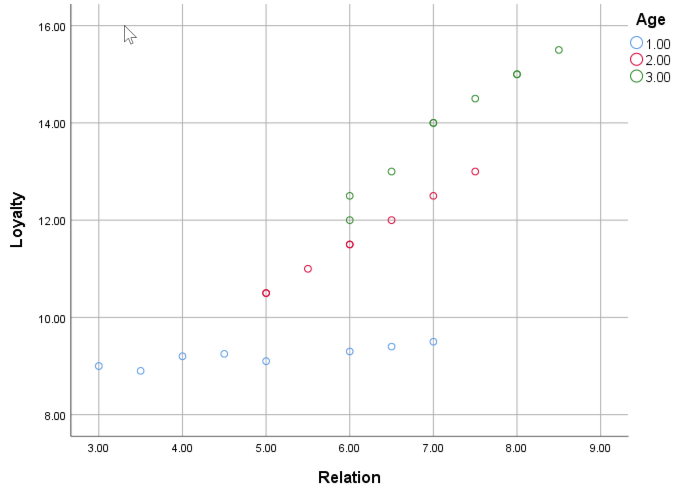
สำหรับบทช่วยสอนนี้ เราจะใช้ชุดข้อมูลตัวอย่างที่มีสามตัวแปร: Relationship, Loyalty และ Age หากคุณต้องการทำตาม ให้ดาวน์โหลดไฟล์ข้อมูล SPSS ตัวอย่างและนำเข้าสู่ SPSS ชุดข้อมูลควรมีลักษณะดังนี้:
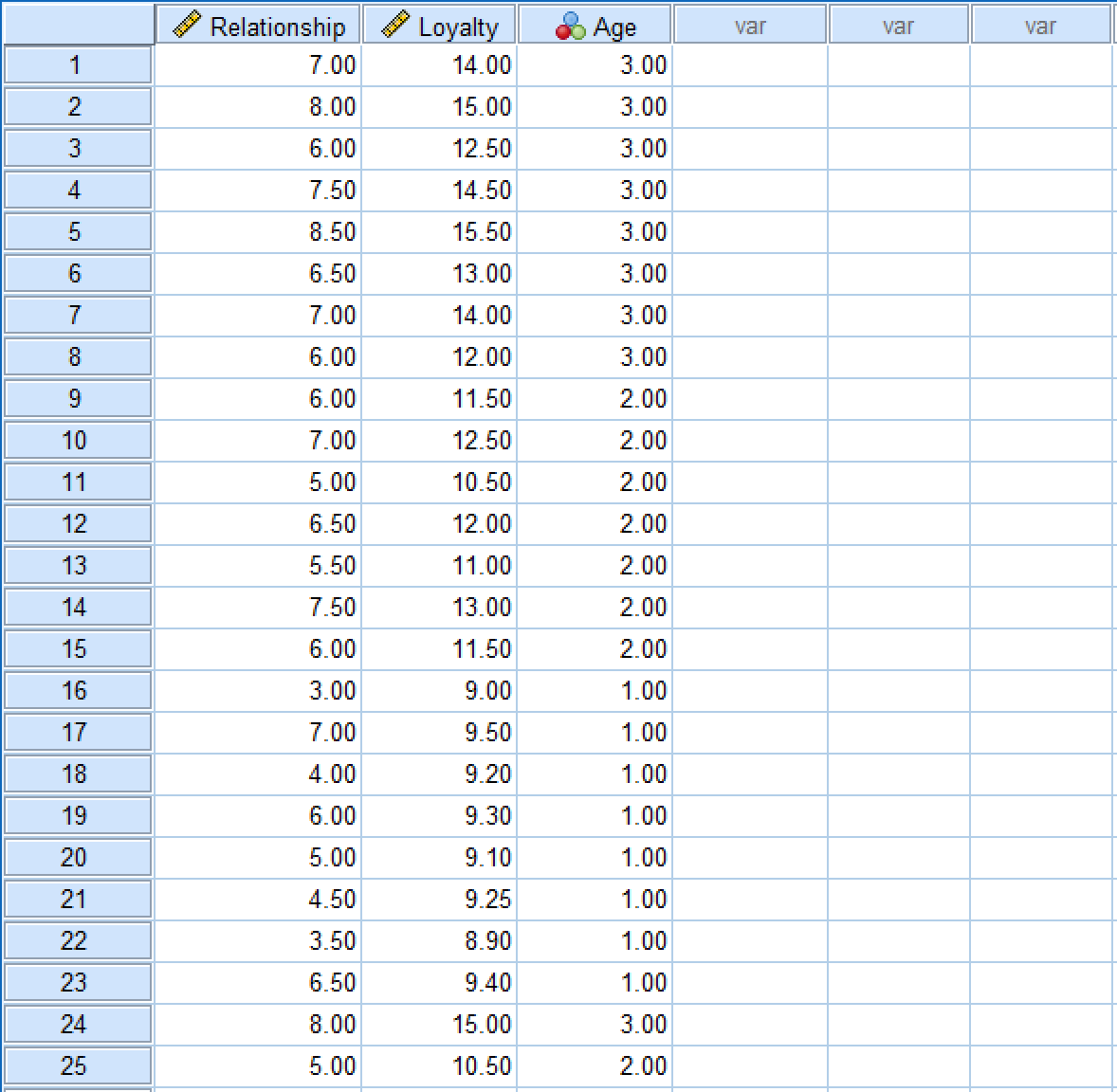 ชุดข้อมูล SPSS ตัวอย่างแสดงตัวแปร Relationship, Loyalty และ Age
ชุดข้อมูล SPSS ตัวอย่างแสดงตัวแปร Relationship, Loyalty และ Age
ขั้นตอนที่ 1: ทำให้ตัวแปรต่อเนื่องเป็นมาตรฐาน
หมายเหตุสำคัญ: ในวิธีด้วยตนเองนี้ เราจะใช้ Z-score standardization (การสร้างคะแนนมาตรฐานที่มีค่าเฉลี่ย = 0 และ SD = 1) ซึ่งแตกต่างจาก mean centering ที่ใช้โดย PROCESS Macro ซึ่งเพียงแค่ลบค่าเฉลี่ย (ค่าเฉลี่ย = 0 แต่คง SD เดิม)
ทั้งสองแนวทางลด multicollinearity ระหว่างเทอมปฏิสัมพันธ์และองค์ประกอบของมัน Z-score standardization มีข้อได้เปรียบในการทำให้ตัวแปรทั้งหมดอยู่บนมาตราส่วนเดียวกัน ทำให้ค่าสัมประสิทธิ์สามารถเปรียบเทียบได้โดยตรง
ทำไมต้องทำให้เป็นมาตรฐาน? เมื่อคุณคูณ X × M เพื่อสร้างเทอมปฏิสัมพันธ์ ตัวแปรที่ได้มักมีความสัมพันธ์สูงกับ X และ M การทำให้เป็นมาตรฐานช่วยลดปัญหานี้และทำให้การตีความง่ายขึ้น
เพื่อทำให้ตัวแปรในชุดข้อมูลของเราเป็นมาตรฐาน ไปที่ Analyze → Descriptive Statistics → Descriptives ในเมนูบนสุดของ SPSS
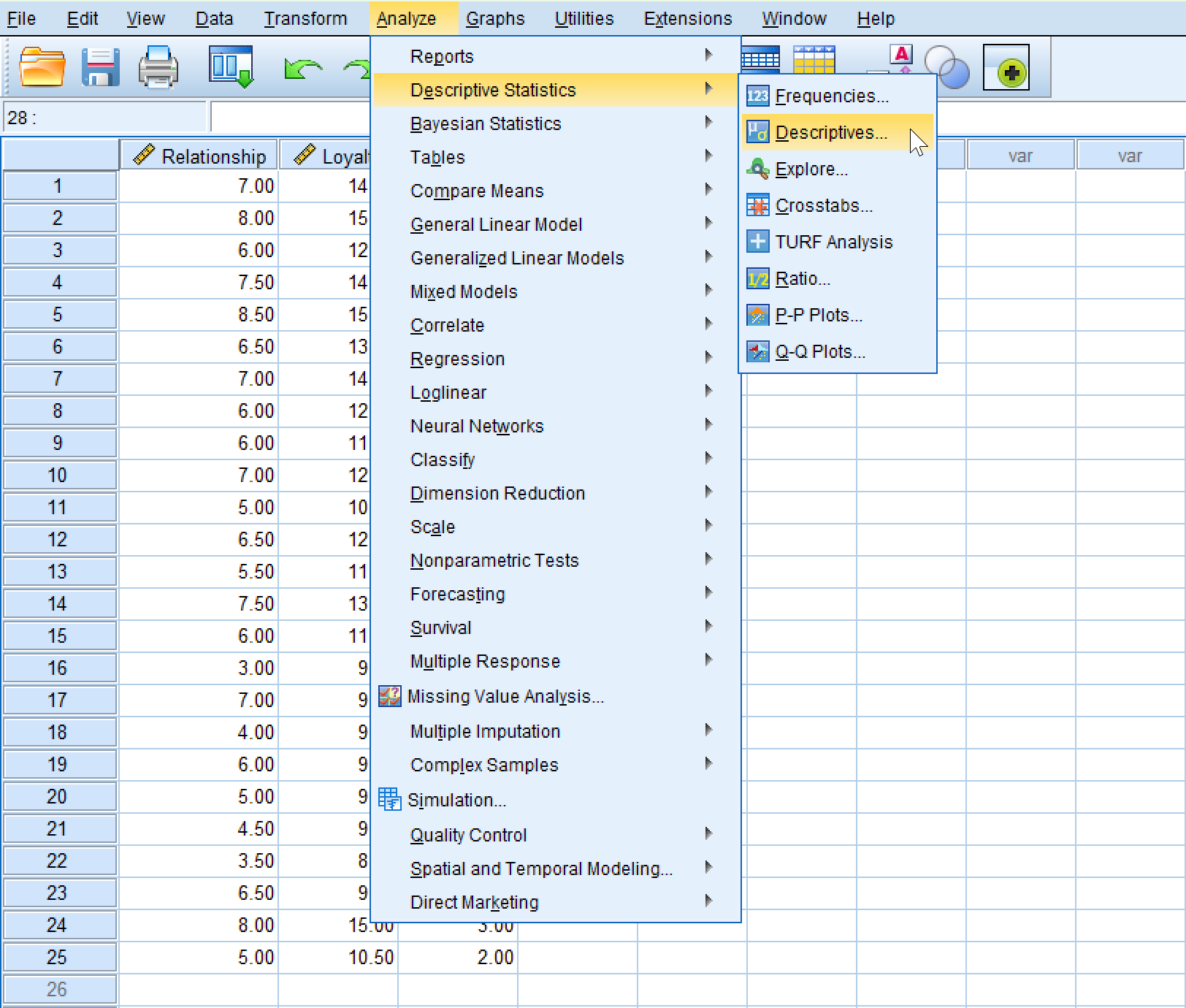 การนำทางไปยัง Descriptive Statistics ใน SPSS เพื่อทำให้ตัวแปรเป็นศูนย์กลาง
การนำทางไปยัง Descriptive Statistics ใน SPSS เพื่อทำให้ตัวแปรเป็นศูนย์กลาง
ในหน้าต่าง Descriptives:
- ย้าย Relationship และ Age ไปยังช่อง Variable(s)
- เลือก "Save standardized values as variables"
- คลิก
OK
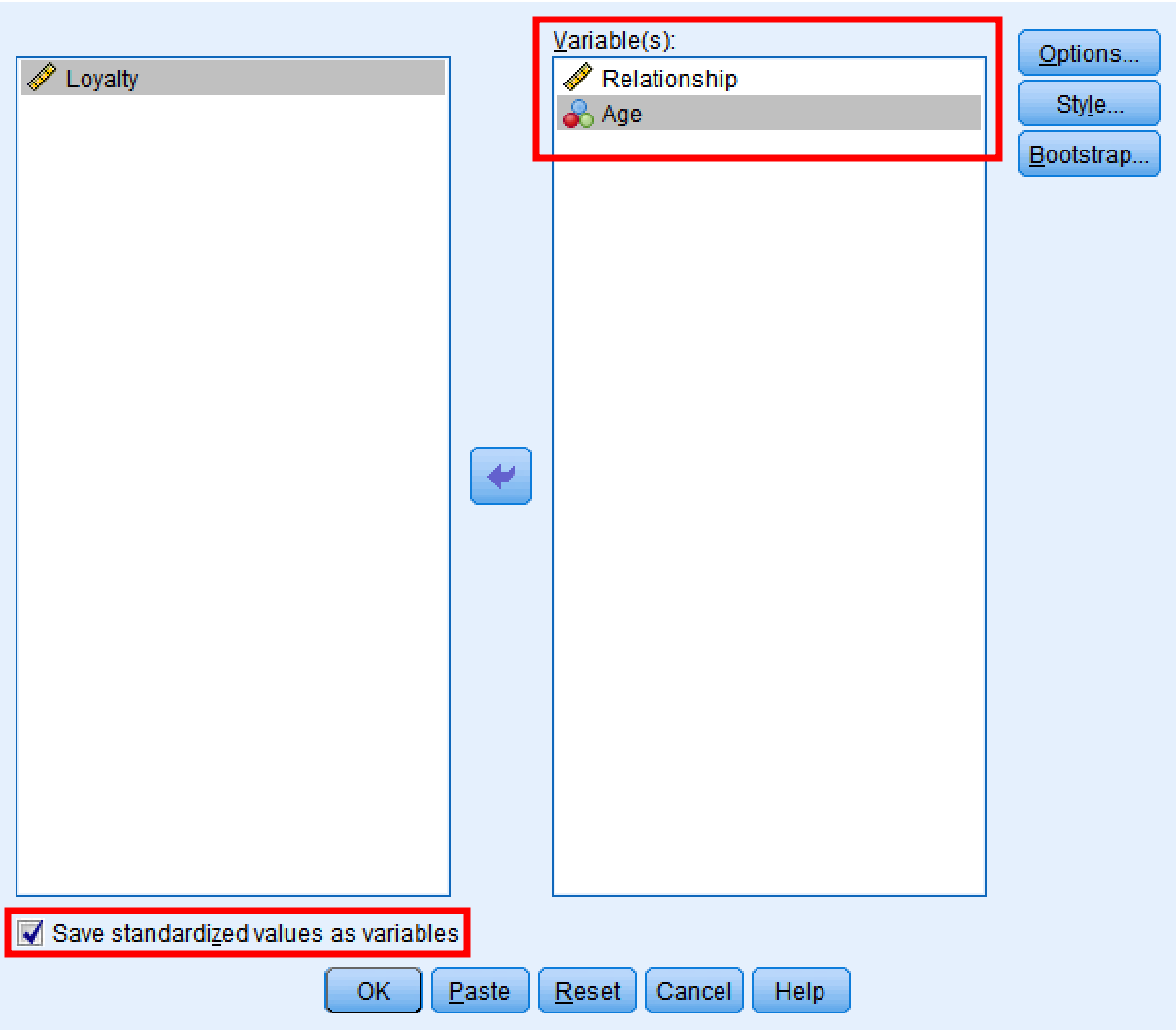 หน้าต่างโต้ตอบ SPSS Descriptives แสดงการเลือกตัวแปรและตัวเลือกการทำให้เป็นมาตรฐาน
หน้าต่างโต้ตอบ SPSS Descriptives แสดงการเลือกตัวแปรและตัวเลือกการทำให้เป็นมาตรฐาน
SPSS จะสร้างตัวแปรใหม่ที่มีคำนำหน้า Z: ZRelationship และ ZAge
 SPSS Data View แสดงตัวแปรเดิมและตัวแปรมาตรฐานที่มีคำนำหน้า Z
SPSS Data View แสดงตัวแปรเดิมและตัวแปรมาตรฐานที่มีคำนำหน้า Z
สิ่งที่การทำให้เป็นมาตรฐานทำ:
| ก่อนการทำให้เป็นมาตรฐาน | หลังการทำให้เป็นมาตรฐาน |
|---|---|
| มาตราส่วนเดิม (เช่น 1-7) | มาตราส่วน Z-score (ค่าเฉลี่ย = 0, SD = 1) |
| ค่าเฉลี่ยแตกต่างกันตามตัวแปร | ค่าเฉลี่ย = 0 สำหรับตัวแปรทั้งหมด |
| หน่วยต่างกัน | หน่วยมาตรฐาน |
การเปรียบเทียบตัวแปรเดิมและตัวแปรมาตรฐาน
ขั้นตอนที่ 2: สร้างเทอมปฏิสัมพันธ์
ตอนนี้สร้าง product term โดยการคูณตัวแปรมาตรฐาน
ใน SPSS:
- ไปที่
Transform→Compute Variable - ใน Target Variable พิมพ์:
INT(ย่อมาจาก interaction term) - ในช่อง Numeric Expression พิมพ์:
ZRelationship * ZAge - คลิก
OK
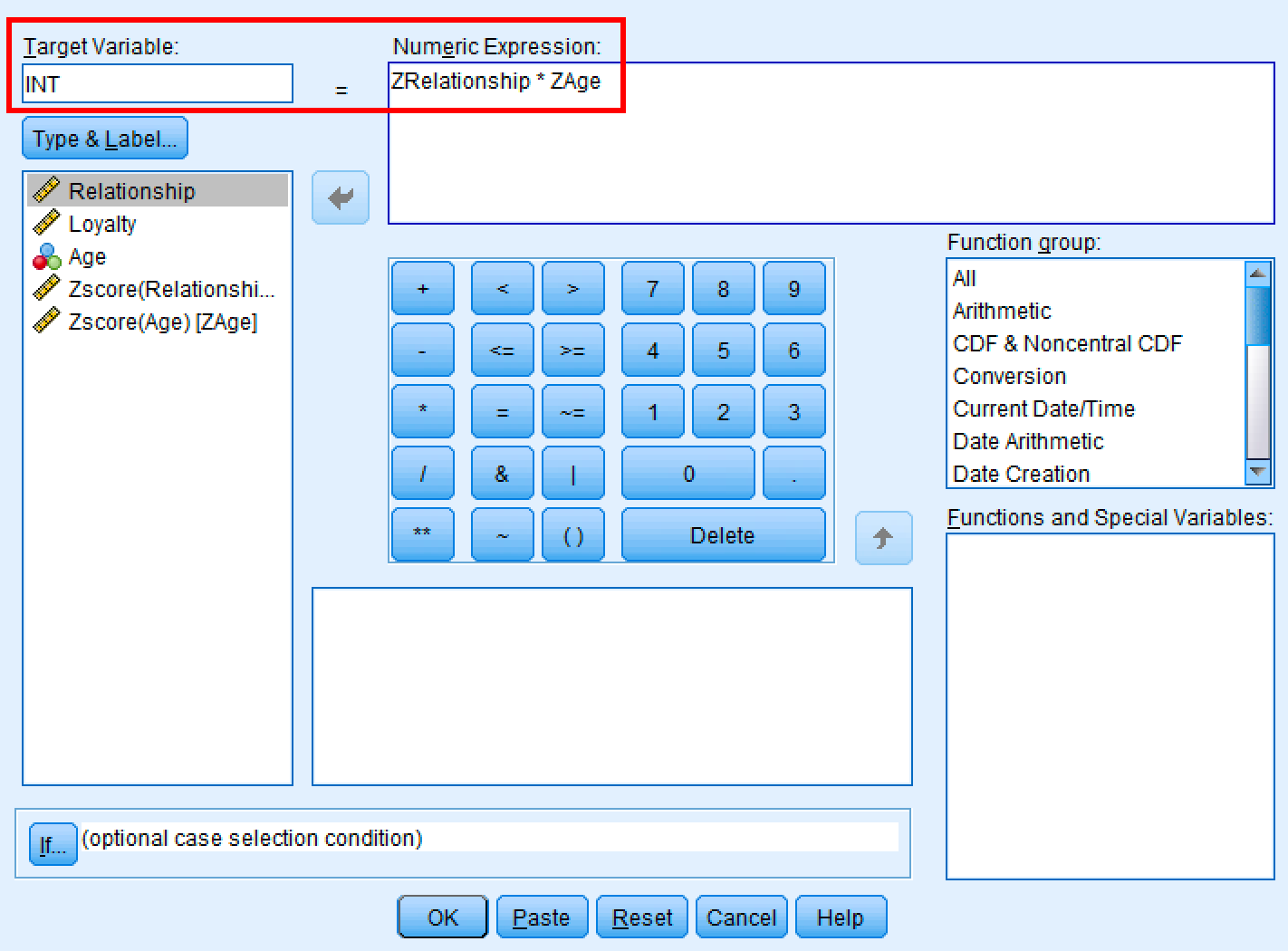 กล่องโต้ตอบ SPSS Compute Variable สำหรับการสร้างเทอมปฏิสัมพันธ์
กล่องโต้ตอบ SPSS Compute Variable สำหรับการสร้างเทอมปฏิสัมพันธ์
SPSS สร้างตัวแปรใหม่ชื่อ INT ที่มีผลคูณของตัวแปรมาตรฐานสองตัว
 SPSS Data View แสดงตัวแปร INT ที่สร้างขึ้นใหม่
SPSS Data View แสดงตัวแปร INT ที่สร้างขึ้นใหม่
ขั้นตอนที่ 3: รันการถดถอยเชิงเส้น
ตอนนี้ทดสอบว่าเทอมปฏิสัมพันธ์ทำนายตัวแปรตามอย่างมีนัยสำคัญหรือไม่
ใน SPSS:
- ไปที่
Analyze→Regression→Linear - ย้าย Loyalty (Y) ไปยังช่อง Dependent
- ย้าย ZRelationship, ZAge และ INT ไปยังช่อง Independent(s)
- คลิก
OK
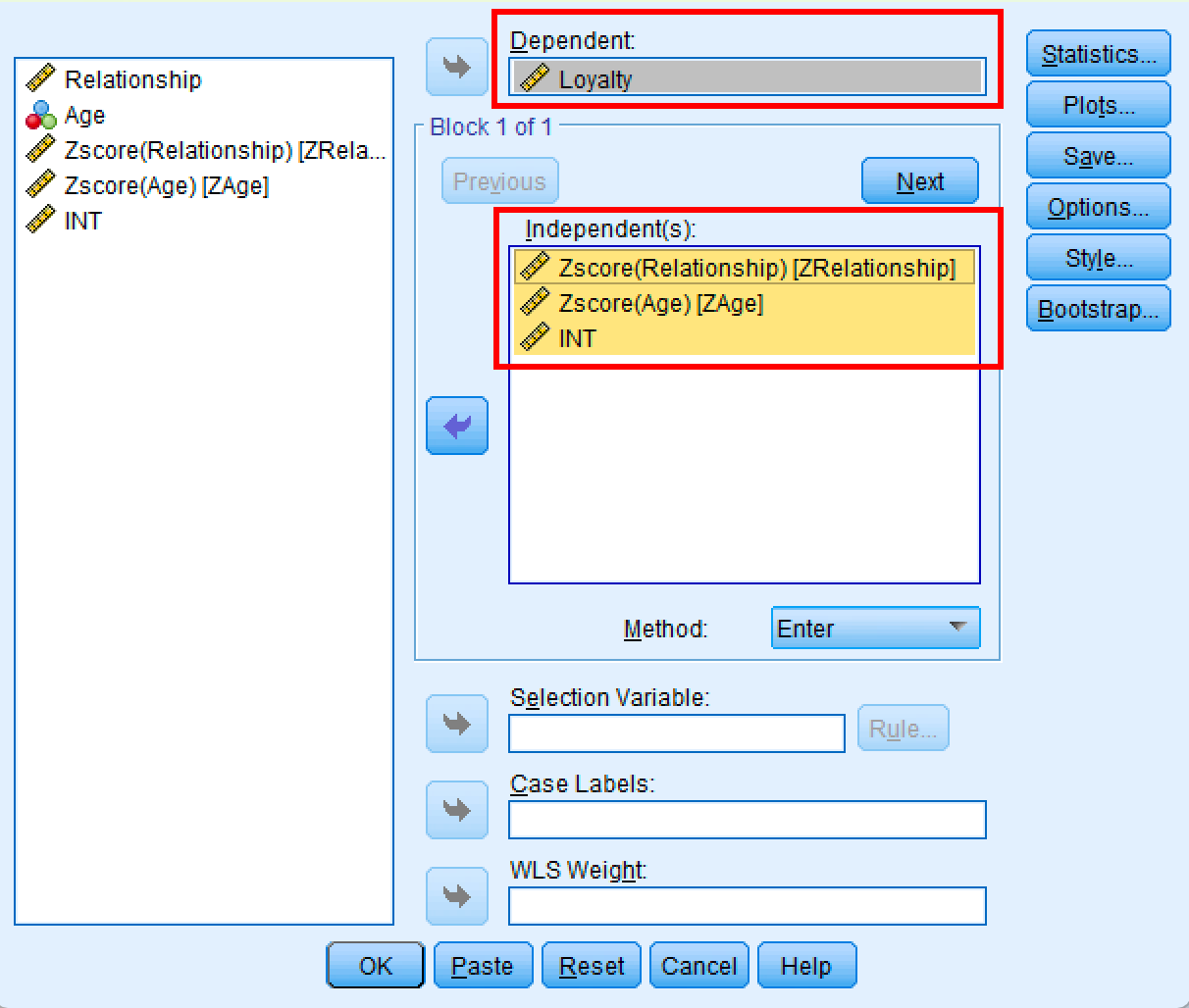 กล่องโต้ตอบ SPSS Linear Regression สำหรับการวิเคราะห์ตัวแปรกำกับ
กล่องโต้ตอบ SPSS Linear Regression สำหรับการวิเคราะห์ตัวแปรกำกับ
การตีความการวิเคราะห์ตัวแปรกำกับใน SPSS
การวิเคราะห์การถดถอยเชิงเส้นสร้างสามตาราง: Model Summary, ANOVA และ Coefficients เพื่อพิจารณาว่า Age กำกับความสัมพันธ์ระหว่าง Relationship และ Loyalty หรือไม่ คุณต้องตรวจสอบค่านัยสำคัญในตาราง Coefficients
ขั้นตอนที่ 1: ตรวจสอบตาราง Model Summary
ก่อนอื่น ดูที่ค่า R Square ในตาราง Model Summary
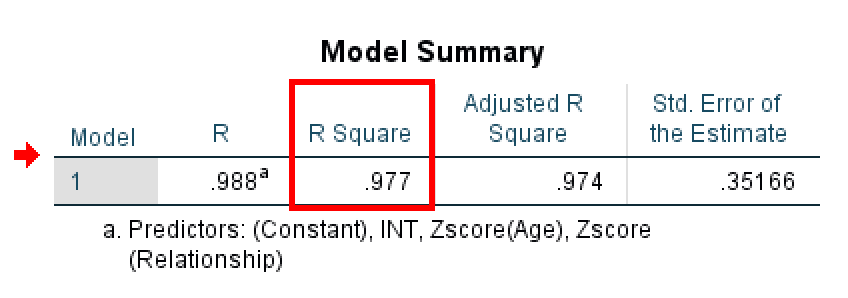 ตาราง Model Summary แสดงค่า R-squared สำหรับโมเดลตัวแปรกำกับ
ตาราง Model Summary แสดงค่า R-squared สำหรับโมเดลตัวแปรกำกับ
R Square บอกคุณว่าความแปรปรวนในตัวแปรตาม (Loyalty) มีเท่าไหร่ที่อธิบายได้โดยโมเดลของคุณ ในตัวอย่างนี้ R Square = 0.977 ซึ่งหมายความว่าโมเดลอธิบาย 97.7% ของความแปรปรวนในความภักดีของลูกค้า
⚠️ หมายเหตุสำคัญเกี่ยวกับตัวอย่างนี้: ค่า R² ของ 0.977 นี้สูงเกินจริงเพราะนี่เป็นข้อมูลจำลองที่สร้างขึ้นเพื่อการสอน ในงานวิจัยจริง ค่า R² สำหรับโมเดลตัวแปรกำกับมักจะอยู่ในช่วง 0.20 ถึง 0.60 อย่าคาดหวังว่าจะเห็นค่า R² สูงแบบนี้ในงานวิจัยจริงของคุณ
ขั้นตอนที่ 2: ตรวจสอบตาราง ANOVA
ถัดไป ตรวจสอบตาราง ANOVA เพื่อทดสอบว่าโมเดลการถดถอยโดยรวมของคุณมีนัยสำคัญทางสถิติหรือไม่
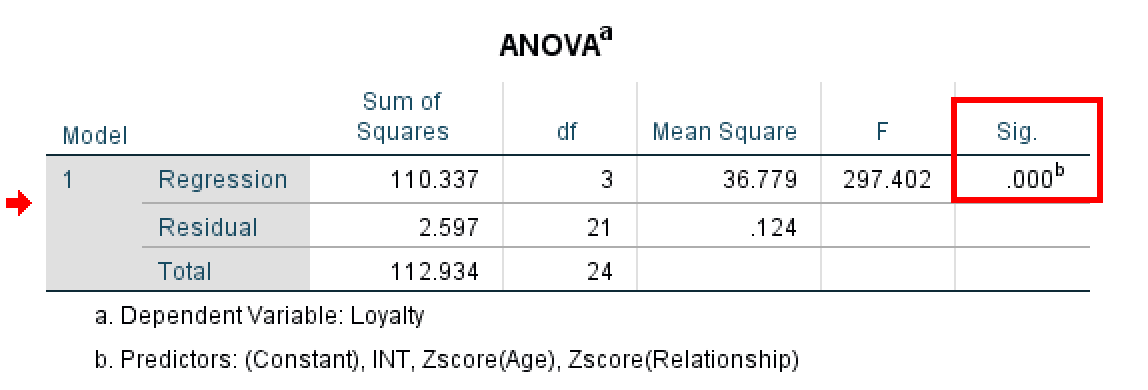 ตาราง ANOVA แสดงนัยสำคัญของโมเดลโดยรวม
ตาราง ANOVA แสดงนัยสำคัญของโมเดลโดยรวม
ตาราง ANOVA ทดสอบว่าโมเดลการถดถอยของคุณ (รวมตัวทำนายทั้งหมด) อธิบายจำนวนความแปรปรวนที่มีนัยสำคัญทางสถิติในตัวแปรผลลัพธ์หรือไม่ ดูที่คอลัมน์ Sig.:
- ถ้า Sig. < 0.05 (มักแสดงเป็น 0.000): โมเดลของคุณมีนัยสำคัญทางสถิติ ตัวทำนายอย่างน้อยหนึ่งตัว (ZRelationship, ZAge หรือ INT) มีผลกระทบที่มีนัยสำคัญต่อ Loyalty
- ถ้า Sig. > 0.05: โมเดลของคุณไม่มีนัยสำคัญ ตัวทำนายไม่อธิบายความแปรปรวนในผลลัพธ์อย่างมีนัยสำคัญ
ในตัวอย่างนี้ ตาราง ANOVA แสดง F = 297.402 โดยที่ Sig. = .000 (p < 0.001) ผลลัพธ์ที่มีนัยสำคัญสูงนี้ยืนยันว่าโมเดลโดยรวมมีนัยสำคัญทางสถิติ
ขั้นตอนที่ 3: ตรวจสอบตาราง Coefficients
สุดท้าย ตรวจสอบตาราง Coefficients เพื่อดูว่าเทอมปฏิสัมพันธ์ (INT) มีนัยสำคัญหรือไม่
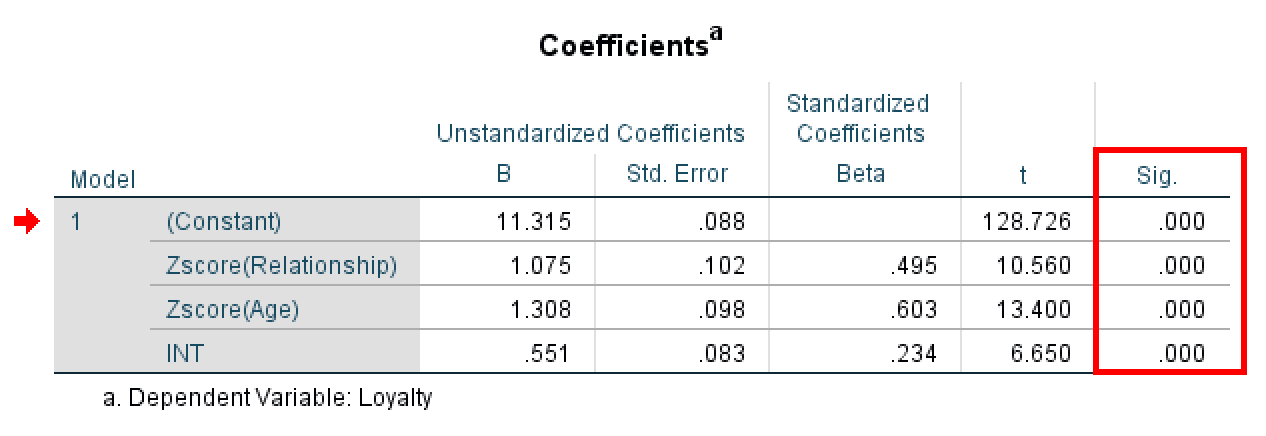 ตารางค่าสัมประสิทธิ์การถดถอย SPSS แสดงผลกระทบปฏิสัมพันธ์
ตารางค่าสัมประสิทธิ์การถดถอย SPSS แสดงผลกระทบปฏิสัมพันธ์
ก่อนที่จะตีความผลลัพธ์ มาทำความเข้าใจว่าแต่ละแถวในตาราง Coefficients บอกคุณอะไร:
| ตัวแปร | สิ่งที่บอกคุณ |
|---|---|
| (Constant) | ค่าพื้นฐานของ Loyalty เมื่อตัวทำนายทั้งหมดเป็นศูนย์ |
| Zscore(Relationship) | ผลกระทบหลักของคุณภาพความสัมพันธ์ต่อความภักดี |
| Zscore(Age) | ผลกระทบหลักของอายุต่อความภักดี |
| INT | ผลกระทบการกำกับ: ความสัมพันธ์ระหว่าง X และ Y เปลี่ยนแปลงขึ้นอยู่กับอายุหรือไม่? |
การทำความเข้าใจตารางค่าสัมประสิทธิ์ในการวิเคราะห์ตัวแปรกำกับ
ตอนนี้ ดูที่แถว INT (เทอมปฏิสัมพันธ์ของคุณ) และตรวจสอบคอลัมน์ Sig.:
- ถ้า Sig. < 0.05: ตัวแปรกำกับ (Age) มีผลกระทบอย่างมีนัยสำคัญต่อความสัมพันธ์ระหว่าง Relationship และ Loyalty มีการกำกับ
- ถ้า Sig. > 0.05: Age ไม่กำกับความสัมพันธ์ ไม่มีผลกระทบการกำกับ
ในตัวอย่างนี้ ค่า Sig. สำหรับ INT คือ .000 (p < 0.001) นี่มีนัยสำคัญสูงมาก ต่ำกว่าเกณฑ์ 0.05 มาก เราสามารถสรุปได้อย่างมั่นใจว่าผลกระทบการกำกับมีนัยสำคัญทางสถิติ นี่หมายความว่า Age กำกับความสัมพันธ์ระหว่าง Relationship และ Loyalty
ขั้นตอนที่ 4: ตีความทิศทาง
เมื่อคุณยืนยันว่าการปฏิสัมพันธ์มีนัยสำคัญแล้ว คุณต้องเข้าใจ ทิศทาง ของผลกระทบการกำกับ ดูที่ค่า B (unstandardized coefficient) ในแถว INT
ในตัวอย่างนี้ ค่า B สำหรับ INT คือ 0.551 เนื่องจากนี่เป็นค่าสัมประสิทธิ์ บวก มันบอกเราว่าความสัมพันธ์ระหว่าง Relationship และ Loyalty กลายเป็น แข็งแกร่งขึ้น เมื่อ Age เพิ่มขึ้น
ความหมายคืออะไร:
ค่าสัมประสิทธิ์บวก (B = 0.551) บ่งชี้ว่าผลกระทบของคุณภาพความสัมพันธ์ต่อความภักดี แข็งแกร่งกว่าสำหรับลูกค้าที่อายุมากกว่า เทียบกับลูกค้าที่อายุน้อยกว่า กล่าวอีกนัยหนึ่ง การสร้างความสัมพันธ์ที่แข็งแกร่งมีผลกระทบที่ใหญ่กว่าต่อความภักดีในหมู่ลูกค้าที่อายุมากกว่าเมื่อเทียบกับผู้ที่อายุน้อยกว่า
การทำความเข้าใจค่าสัมประสิทธิ์บวกเทียบกับลบ:
- ค่าสัมประสิทธิ์บวก (+): ความสัมพันธ์ X→Y แข็งแกร่งขึ้นเมื่อ M เพิ่มขึ้น ค่าที่สูงกว่าของตัวแปรกำกับขยายผลกระทบ
- ค่าสัมประสิทธิ์ลบ (−): ความสัมพันธ์ X→Y อ่อนแอลงเมื่อ M เพิ่มขึ้น ค่าที่สูงกว่าของตัวแปรกำกับลดผลกระทบ
ในตัวอย่างของเรา Age เพิ่มความสัมพันธ์ระหว่างคุณภาพความสัมพันธ์และความภักดี
วิธีที่ 2: PROCESS Macro (แนะนำ)
PROCESS Macro ที่พัฒนาโดย Andrew Hayes เป็นมาตรฐานสมัยใหม่สำหรับการวิเคราะห์ตัวแปรกำกับ มันจัดการการทำให้เป็นมาตรฐานโดยอัตโนมัติ สร้างเทอมปฏิสัมพันธ์ และให้ผลกระทบตามเงื่อนไขที่ระดับต่างๆ ของตัวแปรกำกับ
การติดตั้ง PROCESS Macro
ก่อนที่คุณจะใช้ PROCESS คุณต้องติดตั้งใน SPSS การติดตั้งใช้เวลาประมาณ 5 นาที
สำหรับคำแนะนำการติดตั้งโดยละเอียด ดูคู่มือของเรา: วิธีติดตั้ง PROCESS Macro ใน SPSS
การรันการวิเคราะห์ตัวแปรกำกับด้วย PROCESS
เมื่อติดตั้ง PROCESS แล้ว คุณสามารถเข้าถึงได้จากเมนู SPSS
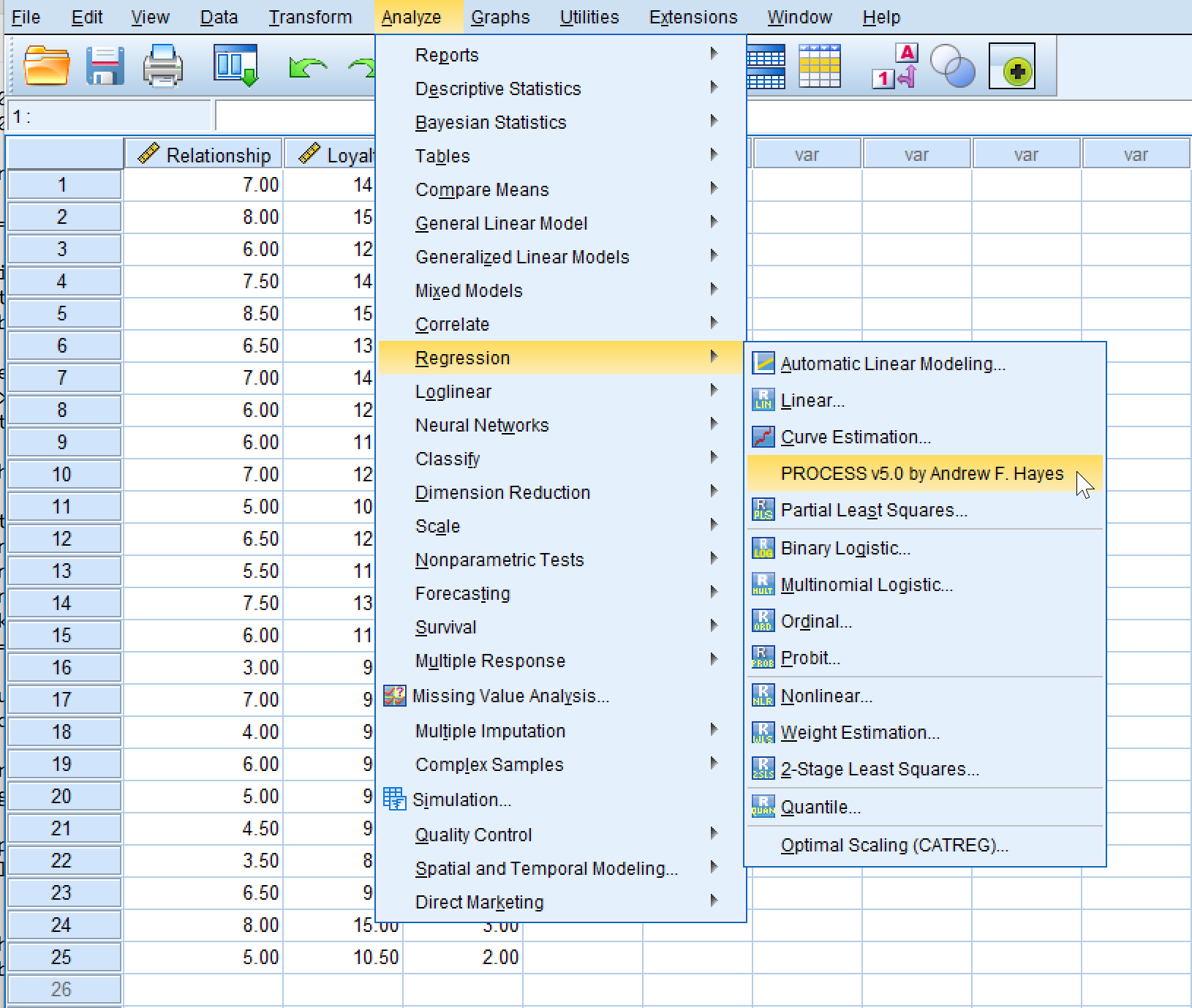 การเข้าถึง PROCESS Macro จากเมนู SPSS: Analyze → Regression → PROCESS
การเข้าถึง PROCESS Macro จากเมนู SPSS: Analyze → Regression → PROCESS
ใน SPSS:
- ไปที่
Analyze→Regression→PROCESS v5.0 by Andrew F. Hayes - เลือก Model 1 (simple moderation model)
- ย้าย Loyalty ไปยังช่อง Y Variable
- ย้าย Relationship ไปยังช่อง X Variable(s)
- ย้าย Age ไปยังช่อง W: Primary Moderator (ไม่ใช่ช่อง M: Mediator)
- ปล่อย M: Mediator(s), Z: Secondary Moderator และ COV: Covariate(s) ว่างไว้
- คลิก
Options
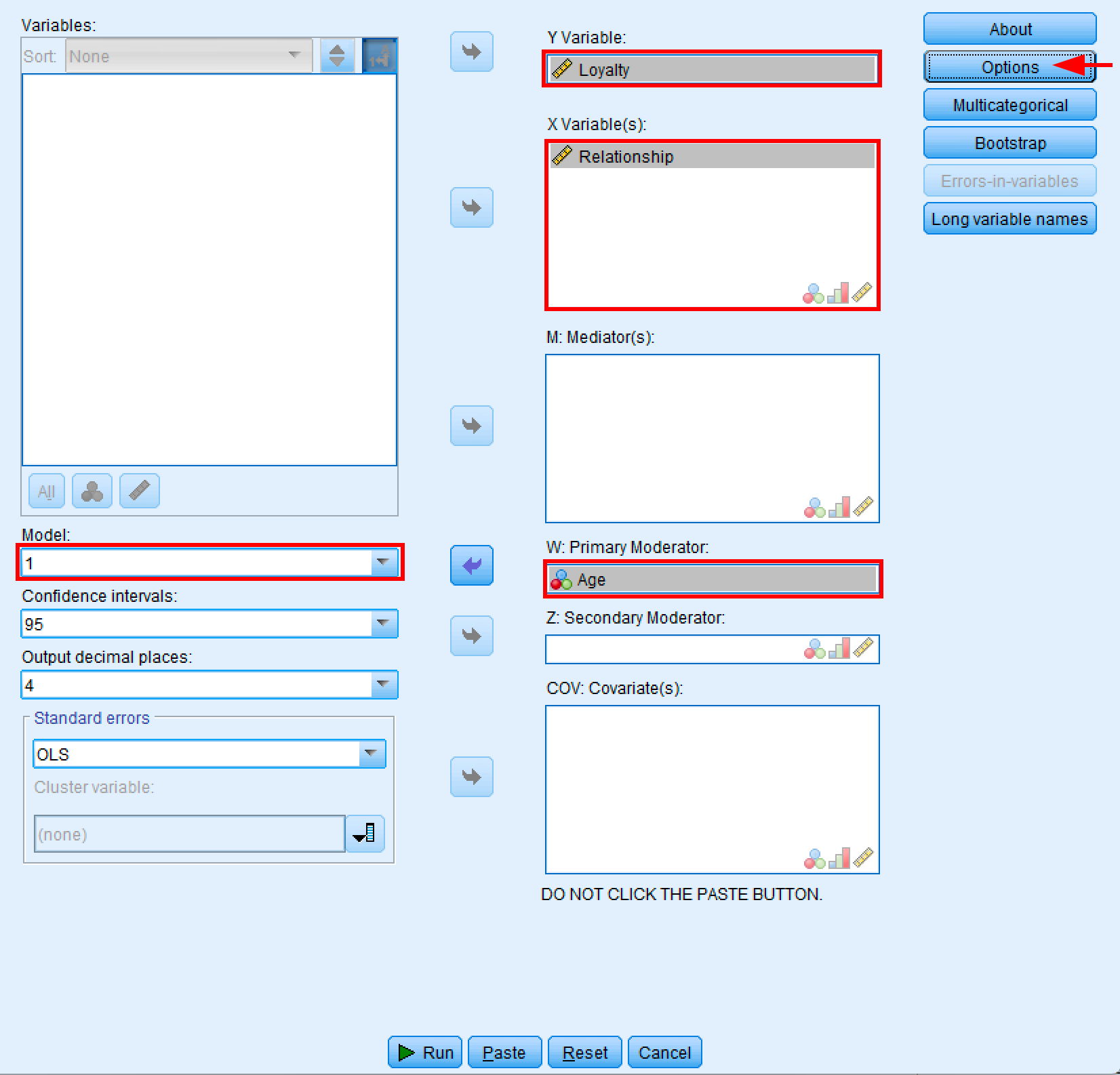 กล่องโต้ตอบ PROCESS Macro ที่ตั้งค่าสำหรับการวิเคราะห์ตัวแปรกำกับแบบง่ายโดยใช้ Model 1
กล่องโต้ตอบ PROCESS Macro ที่ตั้งค่าสำหรับการวิเคราะห์ตัวแปรกำกับแบบง่ายโดยใช้ Model 1
สำคัญ: ตรวจสอบให้แน่ใจว่าคุณวาง Age ในช่อง W: Primary Moderator ไม่ใช่ช่อง M: Mediator(s) ช่อง M สำหรับการวิเคราะห์ตัวแปรคั่นกลาง (โมเดลต่างกัน) ในขณะที่ช่อง W สำหรับตัวแปรกำกับโดยเฉพาะ
ในหน้าต่าง Options:
- ภายใต้ "Centering for moderation:" ตรวจสอบให้แน่ใจว่า "Mean center components of products" ถูกเลือก
- เก็บค่าเริ่มต้น "Continuous and dichotomous components" ที่เลือกไว้
- ภายใต้ "Probing moderation:" ตรวจสอบให้แน่ใจว่า "Probe interactions" ถูกเลือก
- เก็บค่าเริ่มต้น "Percentiles" ที่เลือกไว้สำหรับค่าตัวแปรกำกับ
- เลือก "Johnson-Neyman technique" เพื่อระบุพื้นที่ของนัยสำคัญ
- ภายใต้ "Visualizing moderation:" เลือก "Generate data to visualize moderation"
- คลิก
OK
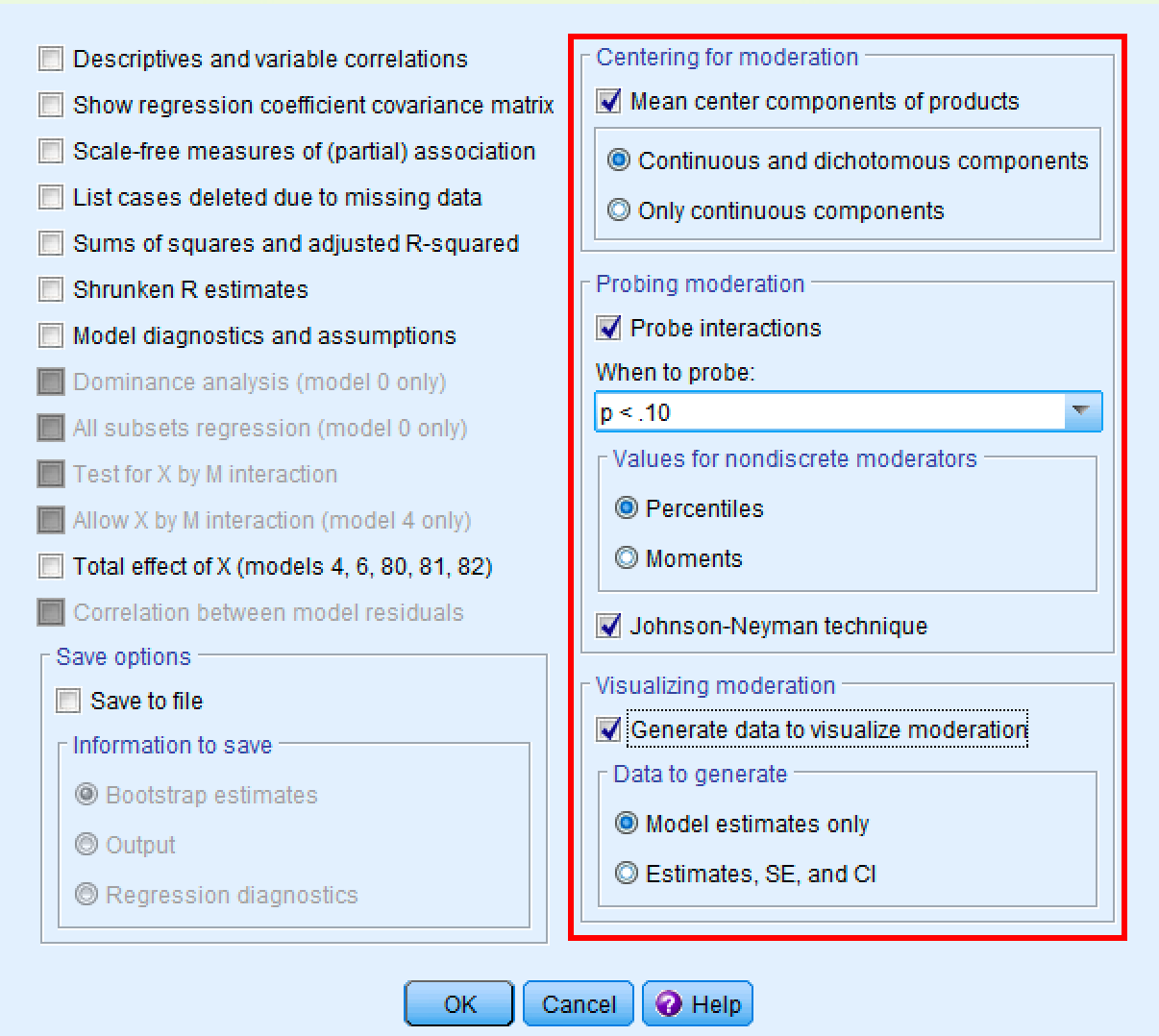 หน้าต่าง PROCESS options แสดงการตั้งค่าที่แนะนำสำหรับการวิเคราะห์ตัวแปรกำกับ
หน้าต่าง PROCESS options แสดงการตั้งค่าที่แนะนำสำหรับการวิเคราะห์ตัวแปรกำกับ
เมื่อคุณตั้งค่าตัวเลือกแล้ว คลิกปุ่ม Run ในหน้าต่าง PROCESS หลัก PROCESS จะทำการวิเคราะห์และสร้างผลลัพธ์ที่ครอบคลุมใน SPSS Output Viewer
การทำความเข้าใจผลลัพธ์ PROCESS
PROCESS สร้างตารางการถดถอยเดียวกับที่คุณเห็นในวิธีที่ 1 แต่จัดการการคำนวณทั้งหมดโดยอัตโนมัติ
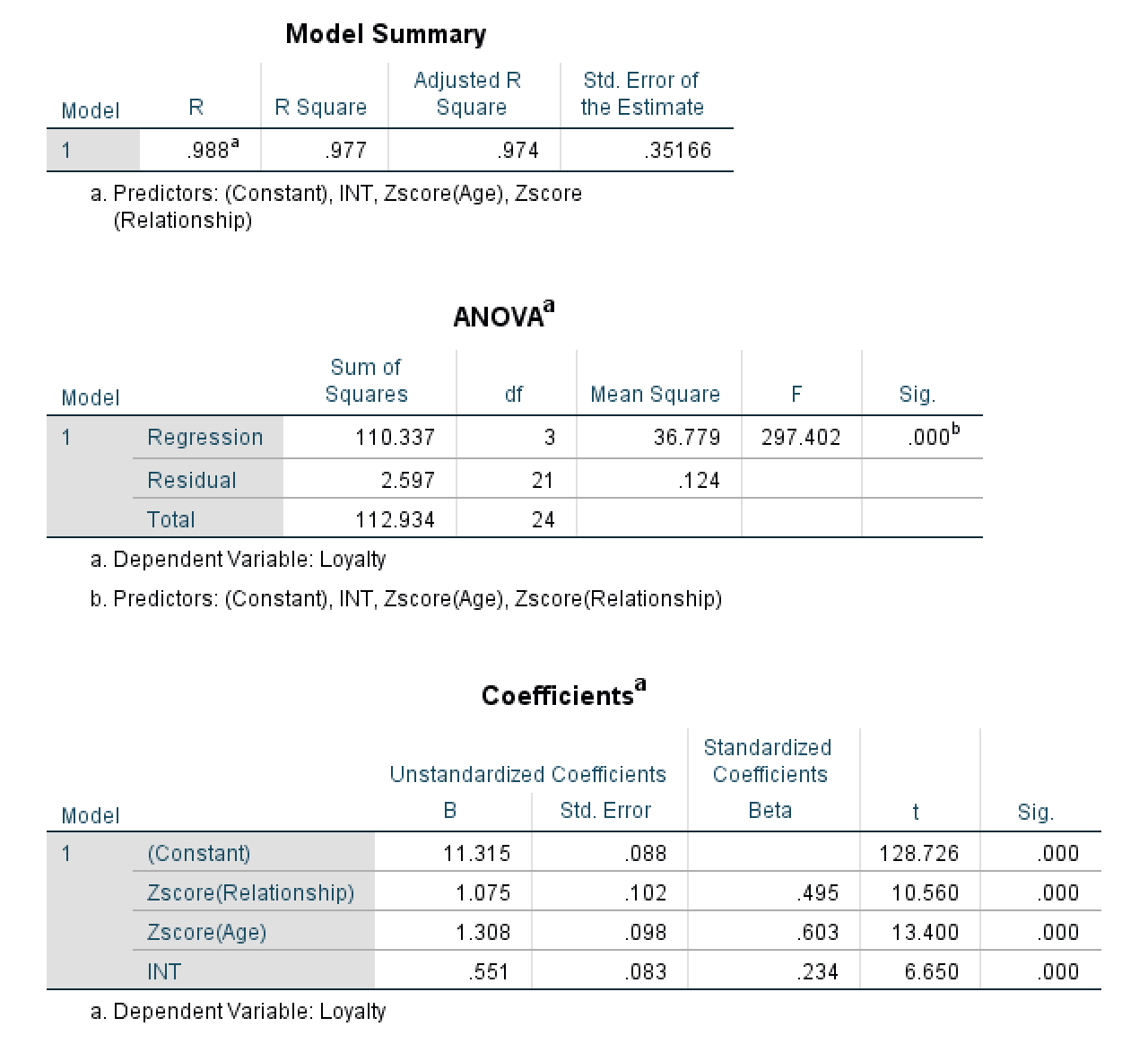 ผลลัพธ์ PROCESS แสดงตาราง Model Summary, ANOVA และ Coefficients
ผลลัพธ์ PROCESS แสดงตาราง Model Summary, ANOVA และ Coefficients
ผลลัพธ์เหมือนกับวิธีที่ 1 (R² = .977, F = 297.402, INT Sig. = .000) ยืนยันผลกระทบการกำกับที่มีนัยสำคัญ
สิ่งที่ PROCESS เพิ่มนอกเหนือจากวิธีที่ 1:
ข้อได้เปรียบที่แท้จริงของ PROCESS คือผลลัพธ์เพิ่มเติมที่ให้:
- ตารางผลกระทบตามเงื่อนไข (Conditional Effects Table): แสดงว่าผลกระทบของ Relationship ต่อ Loyalty เปลี่ยนแปลงอย่างไรที่ระดับ Age ต่างๆ (เช่น ต่ำ ปานกลาง สูง)
- ผลลัพธ์ Johnson-Neyman: ระบุค่า Age ที่แน่นอนที่ผลกระทบการกำกับกลายเป็นมีนัยสำคัญหรือไม่มีนัยสำคัญ
- ข้อมูลการแสดงภาพ: ค่าที่คำนวณล่วงหน้าพร้อมสำหรับการพล็อตการปฏิสัมพันธ์
การตีความ Simple Slopes (ผลกระทบตามเงื่อนไข)
การค้นหาเทอมปฏิสัมพันธ์ที่มีนัยสำคัญบอกคุณว่ามีการกำกับ แต่มันไม่บอกคุณว่า อย่างไร ตัวแปรกำกับมีผลต่อความสัมพันธ์ X→Y นี่คือที่ การวิเคราะห์ simple slopes กลายเป็นสิ่งสำคัญ
Simple Slopes คืออะไร?
Simple slopes (เรียกอีกอย่างว่าผลกระทบตามเงื่อนไข) แทนความสัมพันธ์ระหว่าง X และ Y ที่ค่าเฉพาะของตัวแปรกำกับ แทนที่จะถามว่า "ตัวแปรกำกับมีผลต่อความสัมพันธ์หรือไม่?" (ตอบโดยเทอมปฏิสัมพันธ์) simple slopes ตอบ: "ความสัมพันธ์ X→Y คืออะไรที่ระดับตัวแปรกำกับต่างๆ?"
สำหรับตัวอย่างของเรา simple slopes บอกเรา:
- ผลกระทบของ Relationship ต่อ Loyalty สำหรับ ลูกค้าที่อายุน้อยกว่า คืออะไร?
- ผลกระทบของ Relationship ต่อ Loyalty สำหรับ ลูกค้าอายุปานกลาง คืออะไร?
- ผลกระทบของ Relationship ต่อ Loyalty สำหรับ ลูกค้าที่อายุมากกว่า คืออะไร?
ผลลัพธ์ Conditional Effects ของ PROCESS
เมื่อคุณรัน PROCESS Model 1 โดยเปิดใช้งาน "Probe interactions" PROCESS จะคำนวณ simple slopes โดยอัตโนมัติที่ค่าตัวแปรกำกับสามค่า:
ผลลัพธ์ conditional effects ของ PROCESS แสดงความสัมพันธ์ระหว่าง Relationship Quality และ Loyalty ที่ระดับ Age ต่ำ ปานกลาง และสูง
ความหมายของแต่ละคอลัมน์:
| คอลัมน์ | ความหมาย |
|---|---|
| Age | ค่าตัวแปรกำกับ (ศูนย์กลาง) ลบ = ต่ำกว่าค่าเฉลี่ย, 0 = ค่าเฉลี่ย, บวก = สูงกว่าค่าเฉลี่ย |
| Effect | ความชันของ Relationship→Loyalty ที่ระดับ Age นี้ (นี่คือ simple slope ของคุณ) |
| se | ความคลาดเคลื่อนมาตรฐานของผลกระทบ |
| t | สถิติ T ทดสอบว่า simple slope นี้แตกต่างจากศูนย์อย่างมีนัยสำคัญหรือไม่ |
| p | ค่า P ถ้า p < .05 ความสัมพันธ์ X→Y มีนัยสำคัญที่ระดับตัวแปรกำกับนี้ |
| LLCI, ULCI | ช่วงความเชื่อมั่น 95% ถ้าไม่รวมศูนย์ ผลกระทบมีนัยสำคัญ |
การทำความเข้าใจตาราง conditional effects ของ PROCESS
การเปรียบเทียบสองวิธี
| คุณสมบัติ | วิธีด้วยตนเอง | PROCESS Macro |
|---|---|---|
| ความง่ายในการใช้ | ต้องการการทำให้เป็นมาตรฐานและการสร้างตัวแปรด้วยตนเอง | การทำให้เป็นมาตรฐานและการคำนวณอัตโนมัติ |
| ผลกระทบตามเงื่อนไข | ไม่ให้ | คำนวณโดยอัตโนมัติ |
| การแสดงภาพ | ต้องการการพล็อตด้วยตนเอง | ให้ค่าสำหรับการพล็อตที่ง่าย |
| พลังทางสถิติ | มาตรฐาน | ความคลาดเคลื่อนมาตรฐานที่แข็งแกร่งพร้อมให้บริการ |
| มาตรฐานสมัยใหม่ | การศึกษา | แนวปฏิบัติที่ดีที่สุดในปัจจุบัน |
| คำแนะนำ | ใช้สำหรับการเรียนรู้ | ใช้สำหรับงานวิจัย |
การเปรียบเทียบแนวทางด้วยตนเองและ PROCESS Macro สำหรับการวิเคราะห์ตัวแปรกำกับ
คำถามที่พบบ่อย
สรุป
คุณได้เรียนรู้สองวิธีในการทำการวิเคราะห์ตัวแปรกำกับใน SPSS:
- วิธีด้วยตนเอง: ทำให้ตัวแปรเป็นมาตรฐาน สร้างเทอมปฏิสัมพันธ์ รันการถดถอย (ดีสำหรับการเรียนรู้)
- PROCESS Macro: การวิเคราะห์อัตโนมัติพร้อมผลกระทบตามเงื่อนไขและตัวเลือกที่แข็งแกร่ง (ดีที่สุดสำหรับงานวิจัย)
สำหรับวิทยานิพนธ์หรือโครงการวิจัยของคุณ เราแนะนำ PROCESS Model 1 เพราะให้การทำให้เป็นศูนย์กลางอัตโนมัติ ผลกระทบตามเงื่อนไขที่หลายระดับ และตัวเลือกสำหรับความคลาดเคลื่อนมาตรฐานที่แข็งแกร่ง
จำไว้ว่า: การวิเคราะห์ตัวแปรกำกับเปิดเผย เมื่อใด ความสัมพันธ์เกิดขึ้น ในขณะที่การวิเคราะห์ตัวแปรคั่นกลางเปิดเผย อย่างไร หรือ ทำไม ความสัมพันธ์เกิดขึ้น การเข้าใจความแตกต่างนี้เป็นสิ่งสำคัญสำหรับการเลือกการวิเคราะห์ที่ถูกต้อง
ขั้นตอนถัดไป:
- ดาวน์โหลดข้อมูลตัวอย่างและรันทั้งสองวิธีด้วยตัวคุณเอง
- เรียนรู้การวิเคราะห์ตัวแปรคั่นกลางเพื่อเข้าใจกลไก: How to Run Mediation Analysis in SPSS
- ทำความเข้าใจพื้นฐาน Linear Regression: Linear Regression คืออะไร? วิธีการวิเคราะห์ใน SPSS
- สำรวจการวิเคราะห์ด้วย R: Moderation Analysis ใน R คืออะไร? [Single Moderator]
เอกสารอ้างอิง
Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Hillsdale, NJ: Lawrence Erlbaum Associates.
Hayes, A. F. (2022). Introduction to mediation, moderation, and conditional process analysis: A regression-based approach (3rd ed.). New York: Guilford Press.