การวิเคราะห์ตัวแปรคั่นกลาง (Mediation Analysis) เป็นวิธีการทางสถิติที่ช่วยให้เข้าใจว่า อย่างไร และ เพราะเหตุใด ตัวแปรอิสระ (Independent Variable) มีผลต่อตัวแปรตาม (Dependent Variable) แทนที่จะทดสอบเพียงว่า X มีผลต่อ Y หรือไม่ การวิเคราะห์ตัวแปรคั่นกลางจะสำรวจกลไกพื้นฐาน คือ ตัวแปรคั่นกลาง (Mediator Variable หรือ M) ที่ส่งผ่านผลกระทบจาก X ไปยัง Y
ในคู่มือการวิเคราะห์ตัวแปรคั่นกลางใน SPSS ฉบับสมบูรณ์นี้ คุณจะได้เรียนรู้สองวิธีปฏิบัติในการวิเคราะห์ตัวแปรคั่นกลางใน SPSS:
- วิธี Baron & Kenny (พร้อม Sobel test) — แนวทางการถดถอย 3 ขั้นตอนแบบดั้งเดิม
- วิธี PROCESS Macro (พร้อม bootstrapping) — มาตรฐานสมัยใหม่ที่แนะนำสำหรับงานวิจัย
ชุดข้อมูลตัวอย่าง: ดาวน์โหลดชุดข้อมูลตัวอย่างฟรีเพื่อทำตามทุกขั้นตอน ชุดข้อมูลประกอบด้วยตัวแปรสามตัว: Relationship (คุณภาพความสัมพันธ์), Discount (ส่วนลดส่วนบุคคลที่ได้รับ) และ Satisfaction (ความพึงพอใจของลูกค้า)
ตัวแปรคั่นกลาง คือ อะไร?
การวิเคราะห์ตัวแปรคั่นกลาง (Mediation Analysis) หรือที่เรียกว่า Mediator Analysis ทดสอบว่าความสัมพันธ์ระหว่างตัวแปรอิสระ (X) และตัวแปรตาม (Y) เกิดขึ้นผ่านตัวแปรที่สามที่เรียกว่า ตัวแปรคั่นกลาง (Mediator หรือ M) หรือไม่
คิดแบบนี้: X ไม่มีอิทธิพลต่อ Y โดยตรง แต่ X มีอิทธิพลต่อ M และ M จึงมีอิทธิพลต่อ Y ตัวแปรคั่นกลาง ทำหน้าที่เป็นกลไกหรือเส้นทางที่ X ส่งผลกระทบต่อ Y
ตัวอย่างคำถามวิจัย: "คุณภาพความสัมพันธ์ของลูกค้า (X) เพิ่มความพึงพอใจ (Y) เพราะนำไปสู่ส่วนลดส่วนบุคคลมากขึ้น (M) หรือไม่?"
ในตัวอย่างนี้:
- ตัวแปรต้น (Independent Variable - X): Relationship (คะแนนคุณภาพความสัมพันธ์)
- ตัวแปรคั่นกลาง (Mediator Variable - M): Discount (เปอร์เซ็นต์ส่วนลดส่วนบุคคล)
- ตัวแปรตาม (Dependent Variable - Y): Satisfaction (คะแนนความพึงพอใจของลูกค้า)
ทำความเข้าใจเส้นทางการคั่นกลาง (Mediation Paths)
การวิเคราะห์ตัวแปรคั่นกลางตรวจสอบเส้นทางสำคัญสี่เส้นทาง:
Path A (เส้นทาง A): ผลกระทบของ X ต่อ M (คุณภาพความสัมพันธ์เพิ่มส่วนลดหรือไม่?)
Path B (เส้นทาง B): ผลกระทบของ M ต่อ Y โดยควบคุม X (ส่วนลดเพิ่มความพึงพอใจหรือไม่?)
Path C (เส้นทาง C): ผลกระทบรวม (Total Effect) ของ X ต่อ Y (ความสัมพันธ์โดยรวมก่อนเพิ่มตัวแปรคั่นกลาง)
Path C' (เส้นทาง C'): ผลกระทบทางตรง (Direct Effect) ของ X ต่อ Y โดยควบคุม M (ความสัมพันธ์หลังจากเพิ่มตัวแปรคั่นกลาง)
เมื่อการคั่นกลางเกิดขึ้น ผลกระทบทางตรง (C') จะมีค่าน้อยกว่าผลกระทบรวม (C) หาก C' ลดลงเป็นศูนย์และไม่มีนัยสำคัญ คุณมี full mediation (การคั่นกลางเต็มรูปแบบ) หาก C' ลดลงแต่ยังคงมีนัยสำคัญ คุณมี partial mediation (การคั่นกลางบางส่วน)
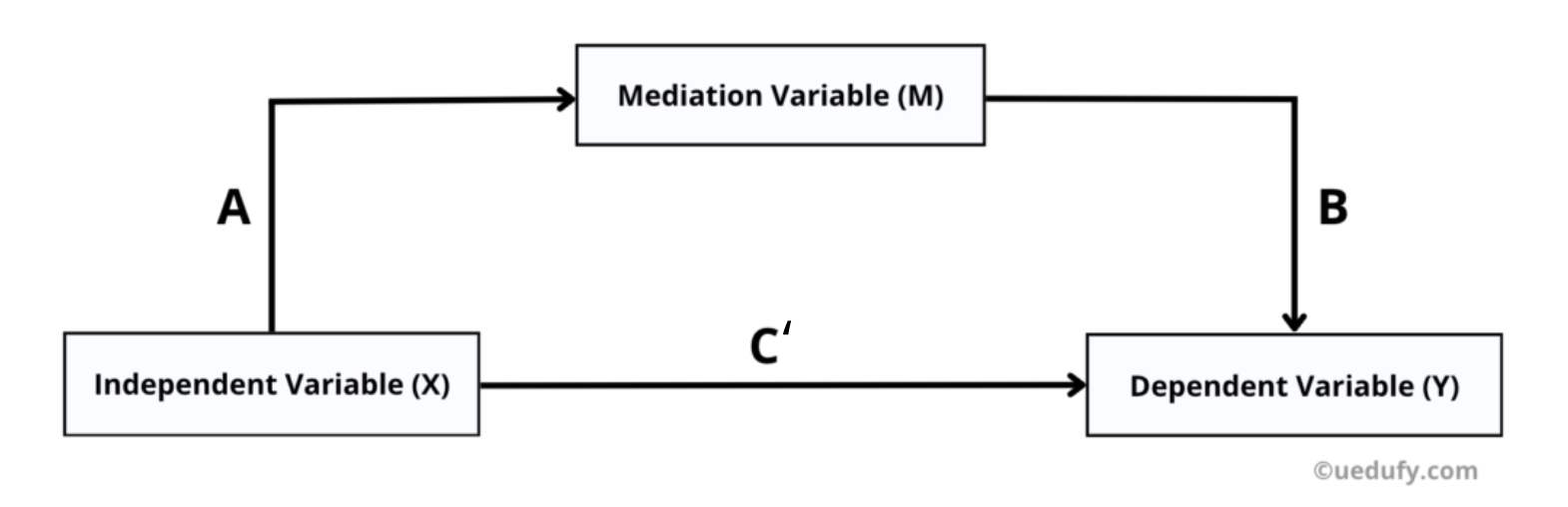 แผนภาพแนวคิดของการวิเคราะห์ตัวแปรคั่นกลาง แสดงความสัมพันธ์ระหว่างตัวแปร X, M และ Y พร้อมเส้นทาง A, B, C และ C'
แผนภาพแนวคิดของการวิเคราะห์ตัวแปรคั่นกลาง แสดงความสัมพันธ์ระหว่างตัวแปร X, M และ Y พร้อมเส้นทาง A, B, C และ C'
วิธีที่ 1: แนวทาง Baron & Kenny
วิธี Baron & Kenny เป็นแนวทางดั้งเดิมในการวิเคราะห์ตัวแปรคั่นกลาง พัฒนาโดยนักวิจัย Baron และ Kenny ในปี 1986 วิธีนี้ใช้การวิเคราะห์การถดถอยแยกกันสามครั้งเพื่อทดสอบการคั่นกลาง
ขั้นตอนที่ 1: ทดสอบผลกระทบรวม (Path C)
ก่อนอื่น ทดสอบว่า X ทำนาย Y ได้อย่างมีนัยสำคัญหรือไม่ โดยไม่มีตัวแปรคั่นกลางในโมเดล
ใน SPSS:
- ไปที่
Analyze→Regression→Linear - ย้าย Satisfaction (Y) ไปยังช่อง Dependent
- ย้าย Relationship (X) ไปยังช่อง Independent(s)
- คลิก
OK
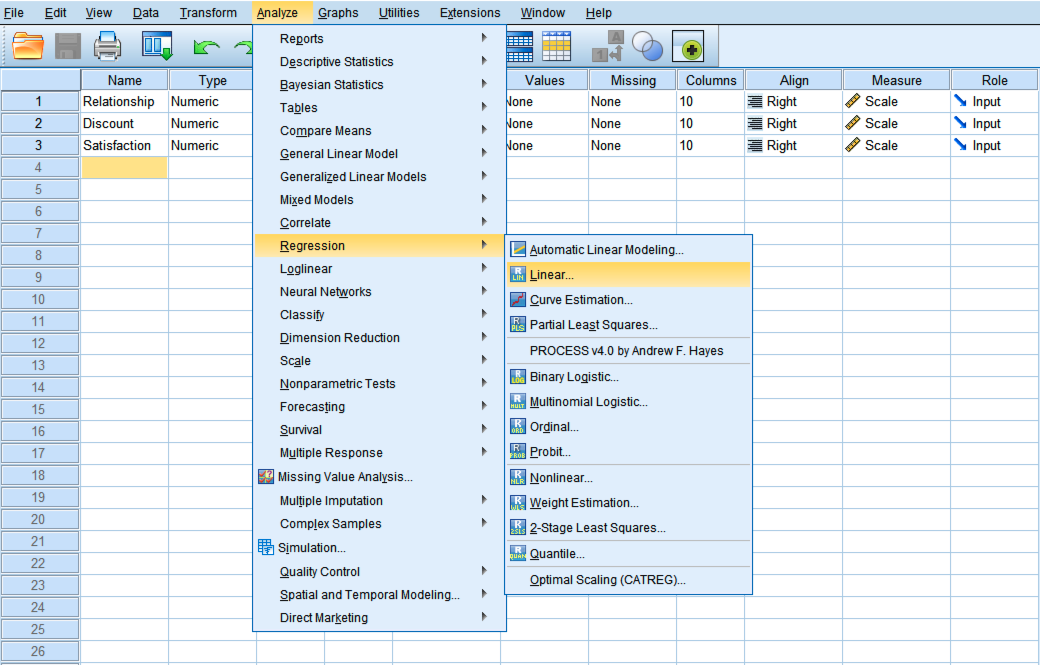 กล่องโต้ตอบ SPSS สำหรับการรันการถดถอยเชิงเส้นเพื่อทดสอบ Path C (ผลกระทบรวม)
กล่องโต้ตอบ SPSS สำหรับการรันการถดถอยเชิงเส้นเพื่อทดสอบ Path C (ผลกระทบรวม)
สิ่งที่ต้องดู:
| สถิติ | การตีความ |
|---|---|
| ค่าสัมประสิทธิ์เบตา (β) | ขนาดและทิศทางของความสัมพันธ์ระหว่าง X และ Y |
| นัยสำคัญ (p-value) | ต้อง < 0.05 จึงจะเป็นไปได้ที่จะมีการคั่นกลาง |
| R-squared (R²) | สัดส่วนความแปรปรวนใน Y ที่อธิบายได้โดย X |
สถิติสำคัญสำหรับการตีความผลกระทบรวมในขั้นตอนที่ 1
หากความสัมพันธ์ระหว่าง X และ Y ไม่มีนัยสำคัญ (p > 0.05) การคั่นกลางอาจจะไม่เกิดขึ้น อย่างไรก็ตาม นักวิจัยบางคนโต้แย้งว่าคุณยังคงสามารถดำเนินการทดสอบผลกระทบทางอ้อมได้
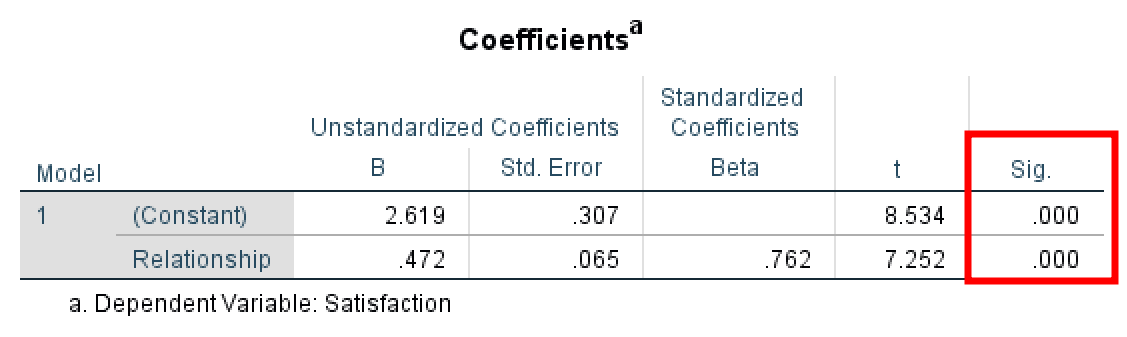 ผลลัพธ์ SPSS แสดงนัยสำคัญของผลกระทบรวม (p = 0.000) บ่งชี้ว่าเราสามารถดำเนินการวิเคราะห์ตัวแปรคั่นกลางต่อได้ Path C = 0.472 (SE = 0.065)
ผลลัพธ์ SPSS แสดงนัยสำคัญของผลกระทบรวม (p = 0.000) บ่งชี้ว่าเราสามารถดำเนินการวิเคราะห์ตัวแปรคั่นกลางต่อได้ Path C = 0.472 (SE = 0.065)
ขั้นตอนที่ 2: ทดสอบ Path A (X → M)
ต่อไป ทดสอบว่า X ทำนาย M ได้อย่างมีนัยสำคัญหรือไม่
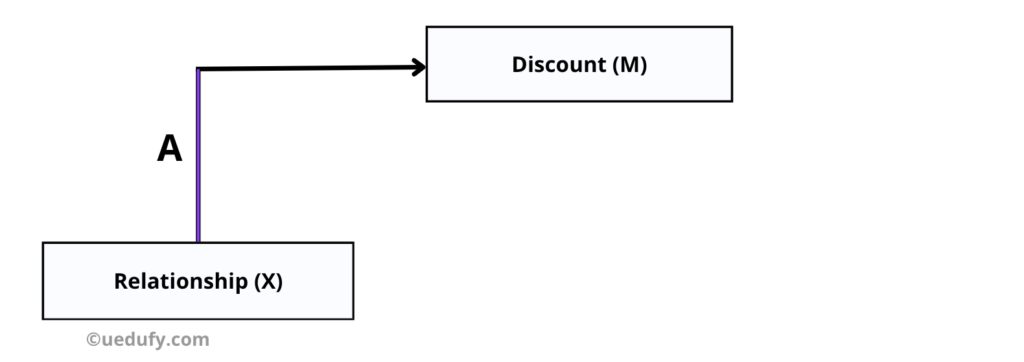 แผนภาพที่แสดง Path A: ผลกระทบของ X (Relationship) ต่อ M (Discounts)
แผนภาพที่แสดง Path A: ผลกระทบของ X (Relationship) ต่อ M (Discounts)
ใน SPSS:
- ไปที่
Analyze→Regression→Linear - กด
Resetเพื่อล้างข้อมูลก่อนหน้า - ย้าย Discount (M) ไปยังช่อง Dependent
- ย้าย Relationship (X) ไปยังช่อง Independent(s)
- คลิก
OK
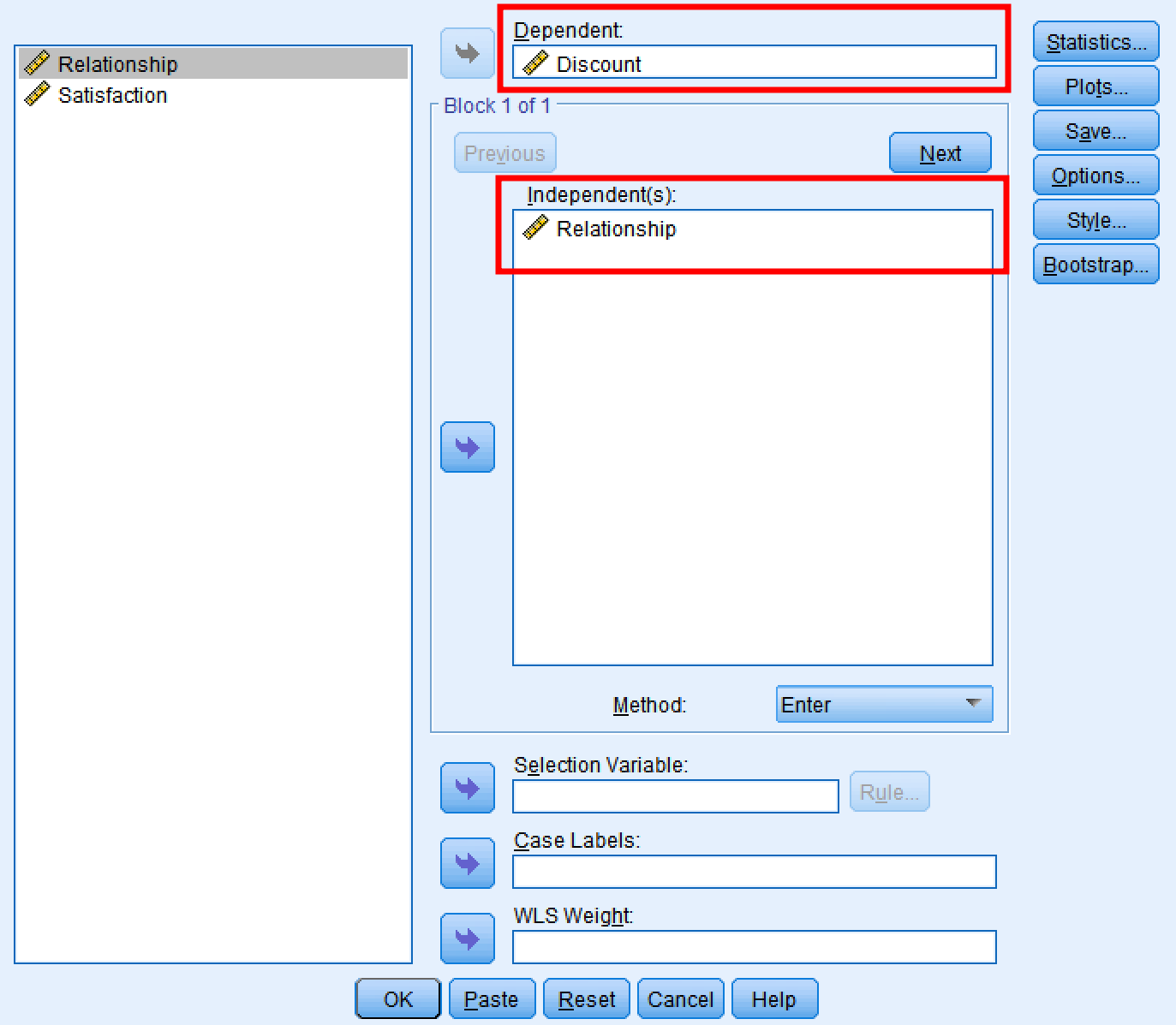 กล่องโต้ตอบ SPSS สำหรับทดสอบ Path A (X → M)
กล่องโต้ตอบ SPSS สำหรับทดสอบ Path A (X → M)
สิ่งที่ต้องดู:
| สถิติ | การตีความ |
|---|---|
| ค่าสัมประสิทธิ์เบตา (β) | ขนาดและทิศทางของผลกระทบของ X ต่อ M |
| นัยสำคัญ (p-value) | ต้อง < 0.05 จึงจะมีการคั่นกลาง |
| R-squared (R²) | X อธิบาย M ได้เท่าไหร่ |
สถิติสำคัญสำหรับการตีความ Path A (X → M) ในขั้นตอนที่ 2
หาก X ไม่ ทำนาย M อย่างมีนัยสำคัญ การคั่นกลางไม่สามารถเกิดขึ้นได้ เพราะตัวแปรคั่นกลางไม่ได้รับอิทธิพลจากตัวแปรอิสระ
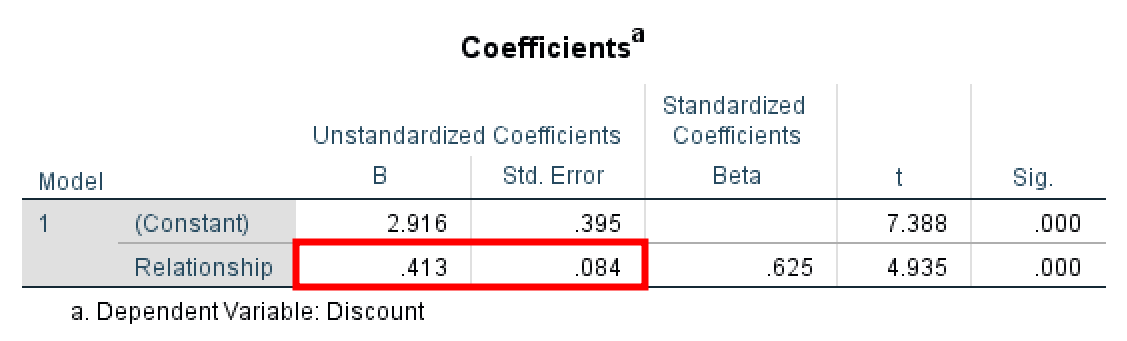 ผลลัพธ์ SPSS แสดง unstandardized coefficient Beta = 0.413 และ Std. Error = 0.084 สำหรับ Path A จดค่าเหล่านี้ไว้สำหรับการคำนวณผลกระทบทางอ้อม
ผลลัพธ์ SPSS แสดง unstandardized coefficient Beta = 0.413 และ Std. Error = 0.084 สำหรับ Path A จดค่าเหล่านี้ไว้สำหรับการคำนวณผลกระทบทางอ้อม
ขั้นตอนที่ 3: ทดสอบ Paths B และ C' (M → Y และ X → Y)
สุดท้าย ทดสอบว่า M ทำนาย Y ได้หรือไม่ขณะที่ควบคุม X และผลกระทบทางตรงของ X ต่อ Y (C') ลดลงหรือไม่
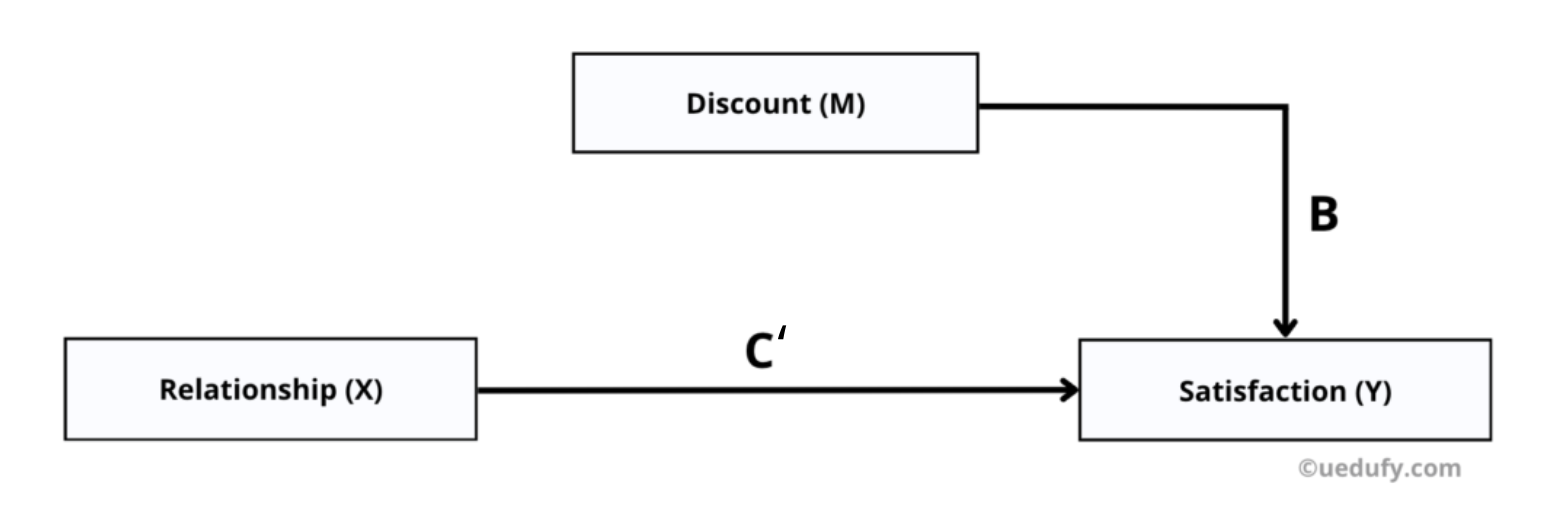 แผนภาพแสดงโมเดลผลกระทบทางตรงที่มีทั้ง X และ M ทำนาย Y (Paths B และ C')
แผนภาพแสดงโมเดลผลกระทบทางตรงที่มีทั้ง X และ M ทำนาย Y (Paths B และ C')
ใน SPSS:
- ไปที่
Analyze→Regression→Linear - กด
Resetเพื่อล้างข้อมูลก่อนหน้า - ย้าย Satisfaction (Y) ไปยังช่อง Dependent
- ย้าย ทั้ง Relationship (X) และ Discount (M) ไปยังช่อง Independent(s)
- คลิก
OK
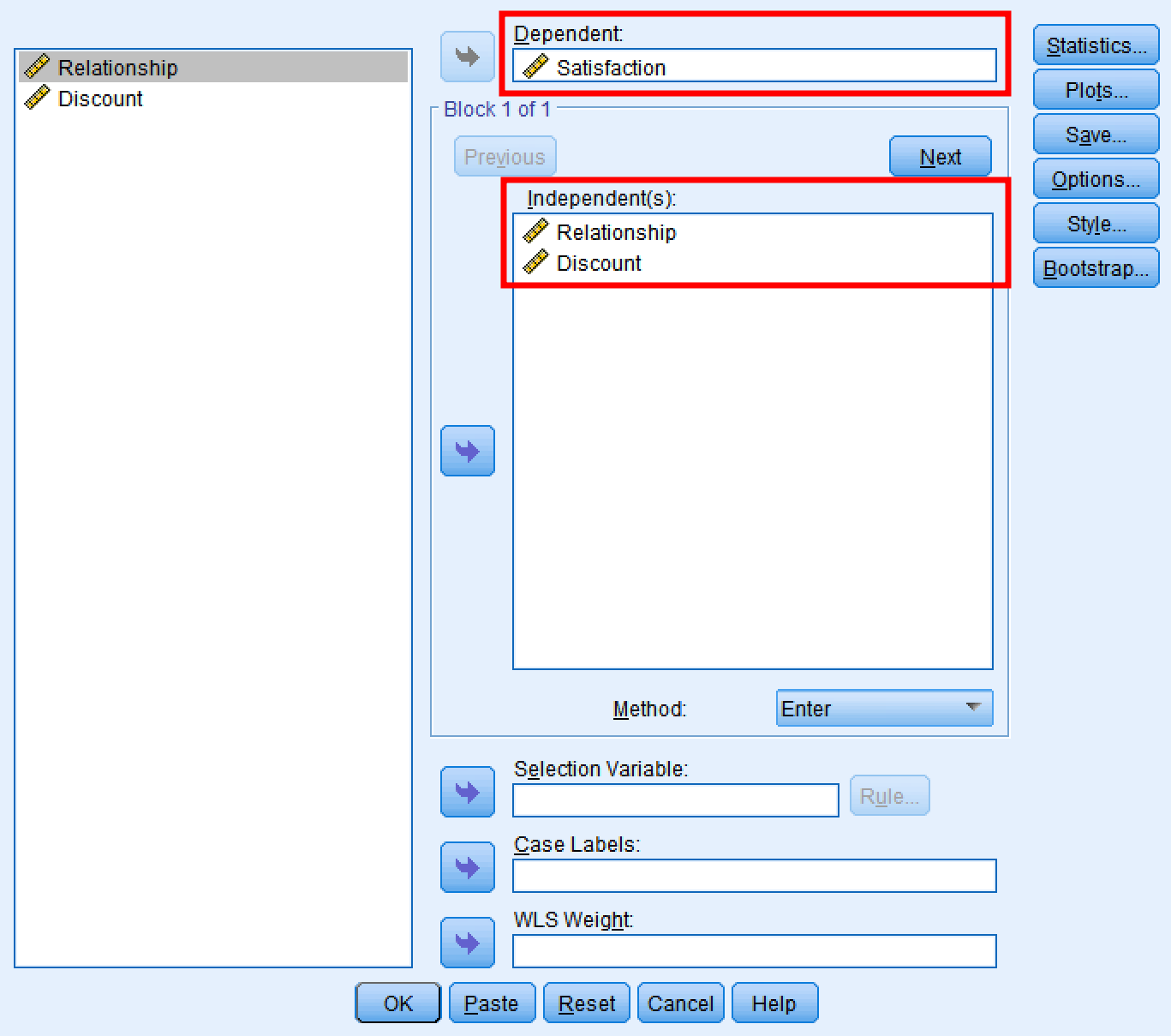 กล่องโต้ตอบ SPSS สำหรับทดสอบ Paths B และ C' โดยรวมทั้ง X และ M เป็นตัวทำนาย
กล่องโต้ตอบ SPSS สำหรับทดสอบ Paths B และ C' โดยรวมทั้ง X และ M เป็นตัวทำนาย
สิ่งที่ต้องดู:
| Path | สถิติ | การตีความ |
|---|---|---|
| Path B (M → Y) | ค่าสัมประสิทธิ์เบตา, p-value | M ต้องทำนาย Y อย่างมีนัยสำคัญ (p < 0.05) |
| Path C' (X → Y) | ค่าสัมประสิทธิ์เบตาเทียบกับ Path C | ควรน้อยกว่า Path C; หากไม่มีนัยสำคัญ มี full mediation |
สถิติสำคัญสำหรับการตีความ Paths B และ C' ในขั้นตอนที่ 3
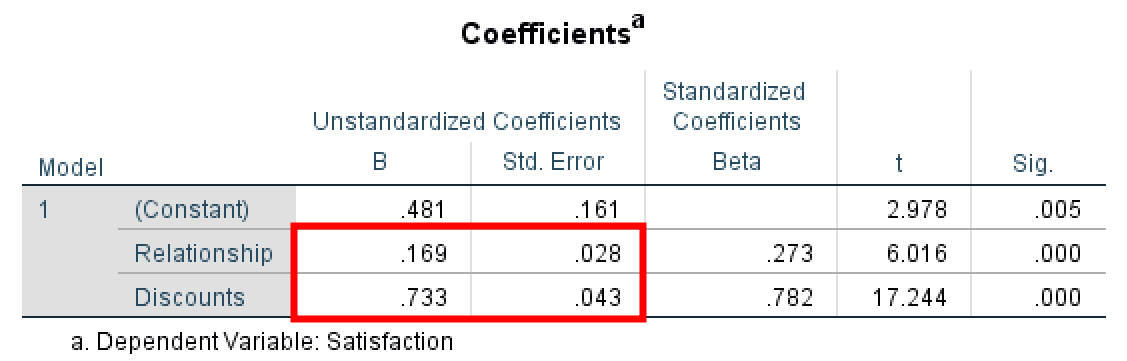 ผลลัพธ์ SPSS แสดง Beta = 0.733 และ Std. Error = 0.043 สำหรับ Path B (Discount → Satisfaction)
ผลลัพธ์ SPSS แสดง Beta = 0.733 และ Std. Error = 0.043 สำหรับ Path B (Discount → Satisfaction)
การคำนวณผลกระทบทางอ้อม (Indirect Effect)
ณ จุดนี้ คุณมีค่าสัมประสิทธิ์ทั้งหมดที่จำเป็นในการประเมินผลกระทบทางอ้อม:
Path A = 0.413 (SE = 0.084) — ผลกระทบของ X ต่อ M (ขั้นตอนที่ 2)
Path B = 0.733 (SE = 0.043) — ผลกระทบของ M ต่อ Y โดยควบคุม X (ขั้นตอนที่ 3)
Path C = 0.472 (SE = 0.065) — ผลกระทบรวมของ X ต่อ Y (ขั้นตอนที่ 1)
Path C' = 0.169 (SE = 0.028) — ผลกระทบทางตรงของ X ต่อ Y โดยควบคุม M (ขั้นตอนที่ 3)
ข้อสังเกตสำคัญ: สังเกตว่า Path C' (0.169) มีค่าน้อยกว่า Path C (0.472) มาก การลดลงนี้แสดงว่าการเพิ่มตัวแปรคั่นกลาง (Discount) อธิบายส่วนสำคัญของความสัมพันธ์ X→Y ผลต่างระหว่างค่าทั้งสองนี้เท่ากับผลกระทบทางอ้อม: 0.472 - 0.169 = 0.303
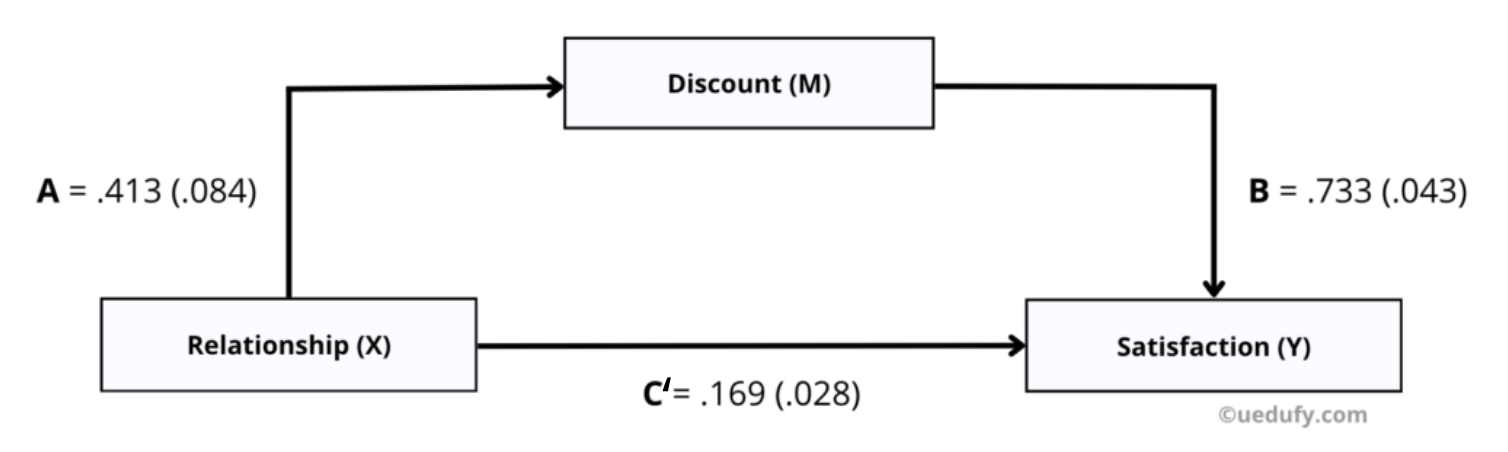 สรุปค่าสัมประสิทธิ์การถดถอยสำหรับเส้นทางการคั่นกลางทั้งหมด หมายเหตุ: Path C' (ผลกระทบทางตรง) = 0.169 ซึ่งน้อยกว่า Path C (ผลกระทบรวม) = 0.472 บ่งชี้ partial mediation
สรุปค่าสัมประสิทธิ์การถดถอยสำหรับเส้นทางการคั่นกลางทั้งหมด หมายเหตุ: Path C' (ผลกระทบทางตรง) = 0.169 ซึ่งน้อยกว่า Path C (ผลกระทบรวม) = 0.472 บ่งชี้ partial mediation
การทดสอบนัยสำคัญด้วย Sobel Test (SPSS Mediation)
เพื่อทดสอบว่าผลกระทบทางอ้อมมีนัยสำคัญทางสถิติหรือไม่ ให้ใช้ Sobel Test สำหรับการคั่นกลาง แม้ว่า SPSS จะไม่มี Sobel test ในตัว แต่คุณสามารถใช้เครื่องคำนวณ Sobel test ออนไลน์ เช่น quantpsy.org/sobel
ป้อนค่าต่อไปนี้ลงในเครื่องคำนวณและคลิก Calculate:
- a = 0.413 (Beta สำหรับ Path A)
- b = 0.733 (Beta สำหรับ Path B)
- s_a = 0.084 (SE สำหรับ Path A)
- s_b = 0.043 (SE สำหรับ Path B)
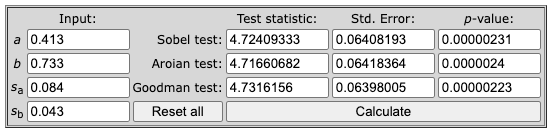 ผลลัพธ์ Sobel Test แสดง test statistic = 4.724, SE = 0.064 และ p-value = 0.0000023
ผลลัพธ์ Sobel Test แสดง test statistic = 4.724, SE = 0.064 และ p-value = 0.0000023
ผลลัพธ์:
- Test statistic = 4.724
- Std. Error = 0.064
- p-value = 0.0000023
เนื่องจาก p < 0.05 ผลกระทบทางอ้อมมีนัยสำคัญทางสถิติ
ค่าประมาณจุดของผลกระทบทางอ้อม (Point Estimate of Indirect Effect):
คำนวณผลกระทบทางอ้อมโดยการคูณ Path A × Path B:
0.413 × 0.733 = 0.303
นี่หมายความว่าผลกระทบทางอ้อมของความสัมพันธ์ต่อความพึงพอใจผ่านส่วนลดคือ 0.303 ที่ p < 0.001
การตีความผลลัพธ์ Baron & Kenny
Full Mediation (การคั่นกลางเต็มรูปแบบ):
- Path C มีนัยสำคัญ (X → Y)
- Path A มีนัยสำคัญ (X → M)
- Path B มีนัยสำคัญ (M → Y)
- Path C' ไม่มีนัยสำคัญ (X → Y โดยควบคุม M)
Partial Mediation (การคั่นกลางบางส่วน):
- Path C มีนัยสำคัญ
- Path A มีนัยสำคัญ
- Path B มีนัยสำคัญ
- Path C' ยังคงมีนัยสำคัญแต่น้อยกว่า Path C
No Mediation (ไม่มีการคั่นกลาง):
- เส้นทางหนึ่งหรือมากกว่าไม่มีนัยสำคัญ
- Path C' ไม่ลดลงอย่างมีความหมาย
วิธีที่ 2: PROCESS Macro สำหรับการวิเคราะห์ตัวแปรคั่นกลางใน SPSS (แนะนำ)
PROCESS Macro สำหรับ SPSS ที่พัฒนาโดย Andrew Hayes เป็นมาตรฐานสมัยใหม่สำหรับการรันการวิเคราะห์ตัวแปรคั่นกลางใน SPSS PROCESS ให้ค่าประมาณของผลกระทบทางอ้อมที่แม่นยำกว่าโดยใช้ bootstrapping และคำนวณช่วงความเชื่อมั่นโดยอัตโนมัติ
การติดตั้ง PROCESS Macro
ก่อนที่คุณจะใช้ PROCESS คุณต้องติดตั้งใน SPSS กระบวนการติดตั้งใช้เวลาประมาณ 5 นาที
สำหรับคำแนะนำการติดตั้งโดยละเอียด ดูคู่มือของเรา: วิธีติดตั้ง PROCESS Macro ใน SPSS
การรันการวิเคราะห์ตัวแปรคั่นกลางด้วย PROCESS ใน SPSS
ใน SPSS:
- ไปที่
Analyze→Regression→PROCESS v5.0 by Andrew F. Hayes - ย้าย Satisfaction (Y) ไปยังช่อง Outcome Variable (Y)
- ย้าย Relationship (X) ไปยังช่อง Independent Variable (X)
- ย้าย Discount (M) ไปยังช่อง Mediator(s) (M)
- เลือก Model 4 (simple mediation model)
- เลือก "Long variable names" หากตัวแปรของคุณมีมากกว่า 8 ตัวอักษร
- คลิก
Options
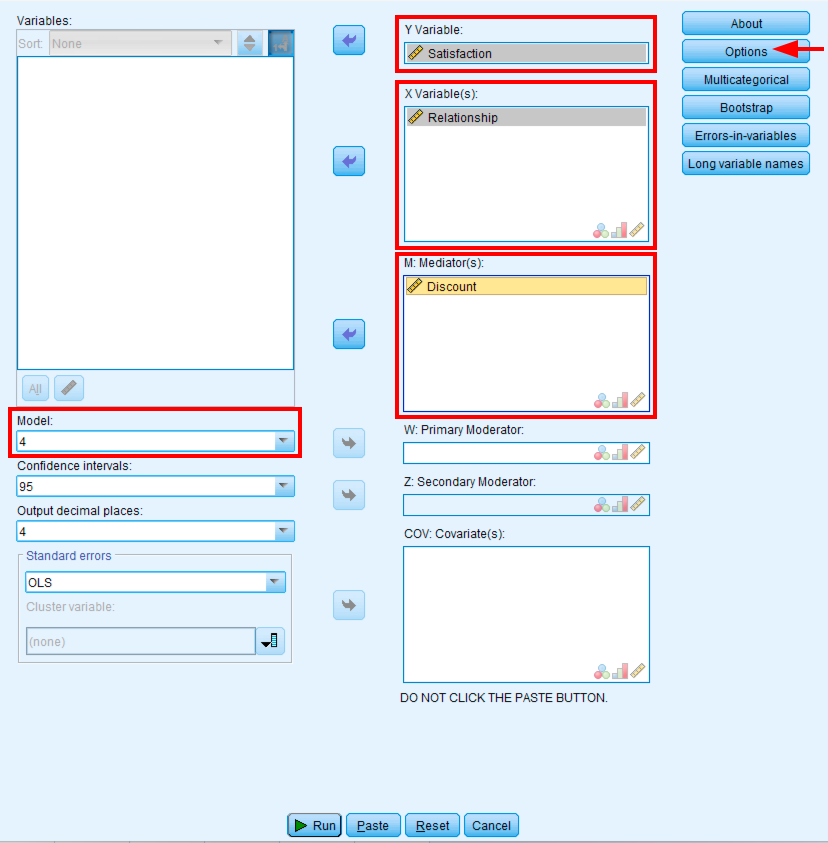 กล่องโต้ตอบ PROCESS Macro ที่ตั้งค่าสำหรับการวิเคราะห์ตัวแปรคั่นกลางแบบง่ายโดยใช้ Model 4
กล่องโต้ตอบ PROCESS Macro ที่ตั้งค่าสำหรับการวิเคราะห์ตัวแปรคั่นกลางแบบง่ายโดยใช้ Model 4
ในหน้าต่าง Options:
- เลือก "Show total effect model (only models 4, 6, 80, 81, 82)"
- เลือก "Standardized effect(s) (mediation-only models)"
- ตั้งค่า bootstrap samples เป็น 5000 (ค่าเริ่มต้น)
- คลิก
Continueจากนั้นคลิกOK
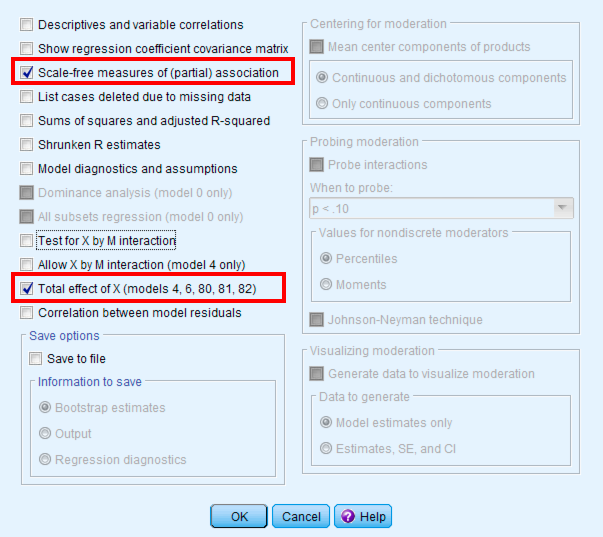 หน้าต่าง PROCESS options แสดงการตั้งค่าที่แนะนำสำหรับการวิเคราะห์ตัวแปรคั่นกลาง
หน้าต่าง PROCESS options แสดงการตั้งค่าที่แนะนำสำหรับการวิเคราะห์ตัวแปรคั่นกลาง
PROCESS จะใช้เวลาสักครู่ในการรันเนื่องจากการคำนวณ bootstrap
ทำความเข้าใจผลลัพธ์ PROCESS
ผลลัพธ์ PROCESS ให้ผลลัพธ์ที่ครอบคลุมสำหรับเส้นทางการคั่นกลางทั้งหมดและผลกระทบทางอ้อม
สรุปโมเดล
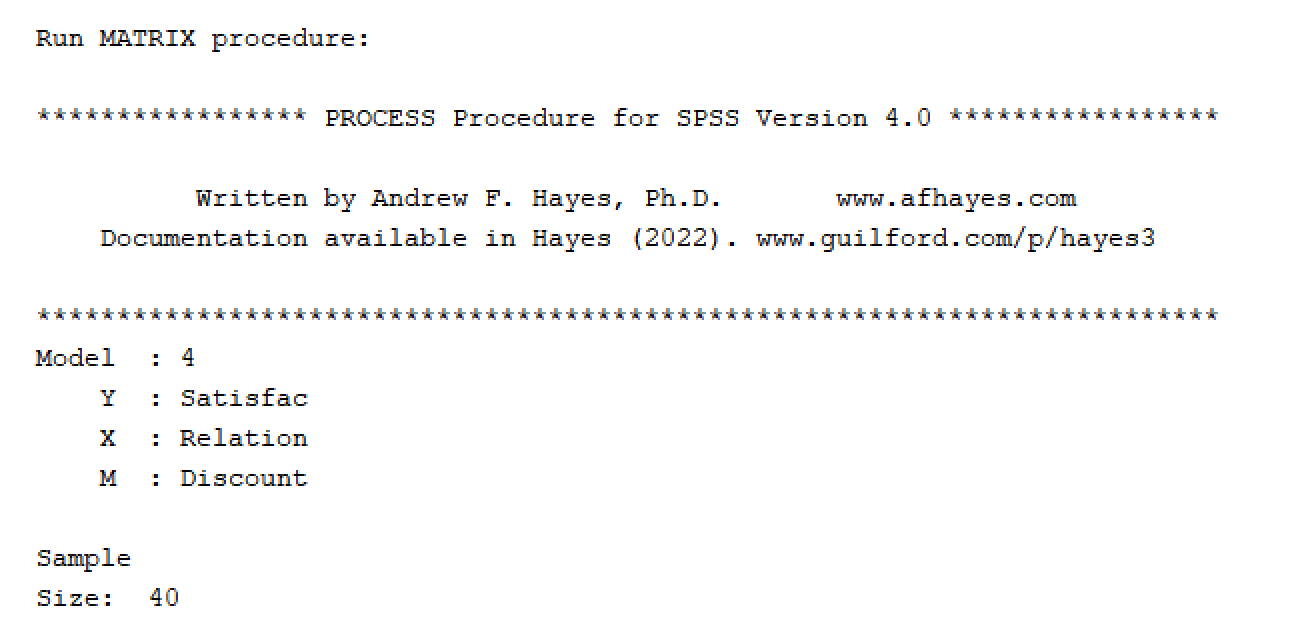 ผลลัพธ์ PROCESS แสดงภาพรวมโมเดลพร้อมตัวแปร X, Y, M และขนาดตัวอย่าง
ผลลัพธ์ PROCESS แสดงภาพรวมโมเดลพร้อมตัวแปร X, Y, M และขนาดตัวอย่าง
Path A: X → M
 ผลลัพธ์ PROCESS สำหรับ Path A แสดงผลกระทบที่มีนัยสำคัญ (p = 0.000) ของ Relationship ต่อ Discount
ผลลัพธ์ PROCESS สำหรับ Path A แสดงผลกระทบที่มีนัยสำคัญ (p = 0.000) ของ Relationship ต่อ Discount
ผลกระทบทางตรงของ Relationship ต่อ Discount มีนัยสำคัญ (p < 0.001)
Paths B และ C': M → Y และ X → Y
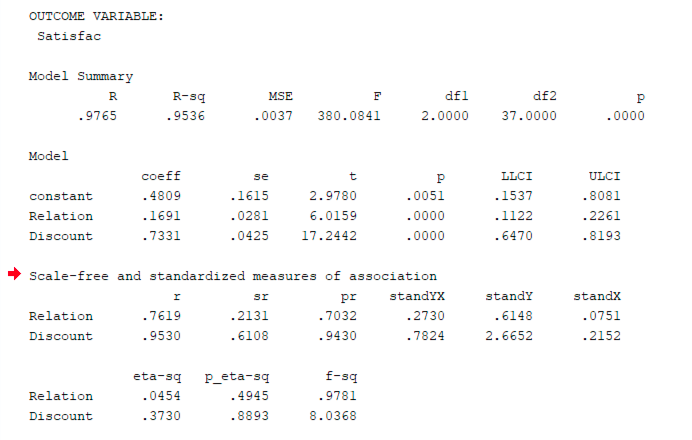 ผลลัพธ์ PROCESS แสดงว่าทั้ง Relationship และ Discount ทำนาย Satisfaction อย่างมีนัยสำคัญ (ทั้งคู่ p = 0.000)
ผลลัพธ์ PROCESS แสดงว่าทั้ง Relationship และ Discount ทำนาย Satisfaction อย่างมีนัยสำคัญ (ทั้งคู่ p = 0.000)
ตัวทำนายทั้งสอง (Relationship และ Discount) มีผลต่อ Satisfaction อย่างมีนัยสำคัญ (ทั้งคู่ p < 0.001)
ผลกระทบทางอ้อมและทางตรง
 ผลลัพธ์ PROCESS แสดงผลกระทบทางอ้อม = 0.303 พร้อมช่วงความเชื่อมั่น bootstrap
ผลลัพธ์ PROCESS แสดงผลกระทบทางอ้อม = 0.303 พร้อมช่วงความเชื่อมั่น bootstrap
ผลลัพธ์สำคัญ:
- Indirect Effect (ผลกระทบทางอ้อม) = 0.303
- Bootstrap Confidence Interval: ไม่รวมศูนย์
- สรุป: มีการคั่นกลางที่มีนัยสำคัญ
การตีความผลลัพธ์ PROCESS
การคั่นกลางที่มีนัยสำคัญ:
- Path a (X → M) มีนัยสำคัญ (p < 0.05)
- Path b (M → Y) มีนัยสำคัญ (p < 0.05)
- ช่วงความเชื่อมั่น bootstrap สำหรับผลกระทบทางอ้อมไม่รวมศูนย์
ประเภทของการคั่นกลาง:
- Full Mediation: Path c' (ผลกระทบทางตรง) ไม่มีนัยสำคัญ (p > 0.05) หรือช่วงความเชื่อมั่นรวมศูนย์
- Partial Mediation: Path c' ยังคงมีนัยสำคัญ (p < 0.05) และช่วงความเชื่อมั่นไม่รวมศูนย์
ช่วงความเชื่อมั่น bootstrapped เป็นมาตรฐานทองคำสำหรับการทดสอบผลกระทบทางอ้อม มันเชื่อถือได้มากกว่า Sobel test เพราะไม่สมมติการแจกแจงแบบปกติของการแจกแจงการสุ่มตัวอย่าง
การตีความผลกระทบทางอ้อม: หมายความว่าอย่างไร?
การค้นหาผลกระทบทางอ้อมที่มีนัยสำคัญเป็นเรื่องดี แต่คุณต้องเข้าใจว่า ตัวเลข บอกอะไรเกี่ยวกับคำถามวิจัยของคุณจริงๆ
ทำความเข้าใจค่าผลกระทบทางอ้อม
ในตัวอย่างของเรา ผลกระทบทางอ้อมคือ 0.303 นี่คือความหมาย:
การตีความ: สำหรับทุก 1 หน่วยที่เพิ่มขึ้นใน Relationship ความพึงพอใจของลูกค้าเพิ่มขึ้น 0.30 หน่วย ผ่านเส้นทางของ Discount นี่คือส่วนของความสัมพันธ์รวมที่ทำงานผ่านตัวแปรคั่นกลาง
การคำนวณสัดส่วนที่ถูกคั่นกลาง (Proportion Mediated)
เพื่อเข้าใจว่าผลกระทบรวมมีเท่าไหร่ที่ทำงานผ่านตัวแปรคั่นกลาง ให้คำนวณสัดส่วนที่ถูกคั่นกลาง:
สูตร: Proportion Mediated = Indirect Effect / Total Effect
ในตัวอย่างของเรา:
- Indirect Effect = 0.303
- Total Effect (Path C) = 0.169 + 0.303 = 0.472
- Proportion Mediated = 0.303 / 0.472 = 64.2%
สิ่งที่บอกคุณ: ประมาณ 64% ของความสัมพันธ์ระหว่าง Relationship และ Satisfaction ทำงานผ่าน Discount อีก 36% ที่เหลือคือผลกระทบทางตรง (ลูกค้าที่มีความสัมพันธ์ที่ดีกว่ามีความพึงพอใจมากขึ้นแม้ไม่มีส่วนลดเพิ่มเติม)
แนวทางขนาดผลกระทบ (Effect Size Guidelines)
ผลกระทบทางอ้อม 0.303 ถือว่าใหญ่แค่ไหน?
แม้ว่าจะไม่มีเกณฑ์สากล แต่นี่คือแนวทางทั่วไปจากงานวิจัยของ Kenny (2018):
| ผลกระทบทางอ้อม (มาตรฐาน) | การตีความ |
|---|---|
| 0.01 ถึง 0.09 | ผลกระทบเล็ก |
| 0.09 ถึง 0.25 | ผลกระทบปานกลาง |
| 0.25 ขึ้นไป | ผลกระทบใหญ่ |
แนวทางขนาดผลกระทบสำหรับผลกระทบทางอ้อมแบบมาตรฐาน (Kenny, 2018)
ในตัวอย่างของเรา: ผลกระทบทางอ้อม 0.303 แสดงถึงผลกระทบขนาดใหญ่ หมายความว่าตัวแปรคั่นกลางมีบทบาทสำคัญในการถ่ายทอดความสัมพันธ์ X→Y
หมายเหตุสำคัญ: การตีความขนาดผลกระทบขึ้นอยู่กับสาขาของคุณ ในจิตวิทยาเชิงทดลอง ผลกระทบเหนือ 0.20 ถือว่าสำคัญ ในการวิจัยธุรกิจเชิงสังเกต ผลกระทบเหนือ 0.15 เป็นที่น่าสังเกต เปรียบเทียบขนาดผลกระทบของคุณกับการศึกษาที่คล้ายกันในสาขาของคุณเสมอ
การตีความผลกระทบทางอ้อมเชิงลบ
ถ้าผลกระทบทางอ้อมของคุณเป็นลบ หมายความว่าตัวแปรคั่นกลางกลับหรือปราบปรามความสัมพันธ์ X→Y นี่เรียกว่า inconsistent mediation หรือ suppression
ตัวอย่าง: ถ้า X ทำนาย M เชิงบวก (path a > 0) แต่ M ทำนาย Y เชิงลบ (path b < 0) ผลกระทบทางอ้อม (a × b) จะเป็นลบ หมายความว่าตัวแปรคั่นกลางทำงานตรงข้ามกับผลกระทบทางตรง
จะเกิดอะไรขึ้นถ้าช่วงความเชื่อมั่นกว้างมาก?
ช่วงความเชื่อมั่นที่กว้าง (เช่น [0.05, 0.80]) บ่งชี้:
- ความแปรปรวนสูง ในการประมาณผลกระทบทางอ้อมของคุณ
- ขนาดตัวอย่างเล็ก (คุณต้องการข้อมูลมากขึ้นเพื่อการประมาณที่แม่นยำ)
- ความคลาดเคลื่อนในการวัด ในตัวแปรของคุณ
วิธีแก้: เพิ่มขนาดตัวอย่างหรือปรับปรุงความเชื่อถือของการวัดตัวแปรของคุณ การวิเคราะห์ตัวแปรคั่นกลางต้องการกำลังเพียงพอ — ตั้งเป้าที่ n > 200 เพื่อการประมาณที่มั่นคง
ทำไม Bootstrapping ใน SPSS จึงดีกว่า Sobel Test
ถ้าคุณใช้การวิเคราะห์ตัวแปรคั่นกลางสำหรับการตีพิมพ์ การเข้าใจว่าทำไม bootstrapping จึงดีกว่า Sobel test เป็นเรื่องสำคัญ
ปัญหาของ Sobel Test
Sobel test มีสมมติฐานที่แข็งแรงที่นักวิจัยหลายคนไม่ทราบ: มันสมมติว่าผลกระทบทางอ้อมมีการแจกแจงแบบปกติ
ทำไมนี่จึงเป็นปัญหา:
ผลกระทบทางอ้อมคำนวณเป็น a × b (ผลคูณของค่าสัมประสิทธิ์การถดถอยสองตัว) เมื่อคุณคูณตัวแปรสองตัว การแจกแจงที่ได้คือ:
- เบ้ (ไม่สมมาตร)
- ไม่ปกติ (โดยเฉพาะในตัวอย่างขนาดเล็ก)
- Leptokurtic (มีหางหนัก)
Bootstrapping แก้ปัญหานี้อย่างไร
Bootstrapping ไม่สมมติความเป็นปกติ แต่:
- สุ่มตัวอย่างข้อมูลของคุณใหม่ 5,000 ครั้ง (ด้วยการแทนที่)
- คำนวณผลกระทบทางอ้อมใหม่ สำหรับแต่ละการสุ่มตัวอย่างใหม่
- สร้างการแจกแจงเชิงประจักษ์ ของผลกระทบทางอ้อมจากข้อมูลจริงของคุณ
- คำนวณช่วงความเชื่อมั่น จากเปอร์เซ็นไทล์ที่ 2.5 และ 97.5 ของการแจกแจงนี้
ข้อได้เปรียบหลัก: ช่วงความเชื่อมั่น bootstrap ขึ้นอยู่กับการแจกแจงจริงของข้อมูลของคุณ ไม่ใช่สมมติฐานทางทฤษฎีเกี่ยวกับความเป็นปกติ
เมื่อไหร่ควรใช้แต่ละวิธี
| วิธี | เมื่อไหร่ควรใช้ | ข้อกำหนดขนาดตัวอย่าง |
|---|---|---|
| Sobel Test | เฉพาะสำหรับตัวอย่างขนาดใหญ่มากหรือเมื่อคุณไม่มีข้อมูลดิบ | n > 500 (Fritz & MacKinnon, 2007) |
| Bootstrap | ทุกสถานการณ์การวิจัย (แนะนำ) | n > 50 (ตัวอย่างเล็กกว่ายอมรับได้) |
| Monte Carlo | เมื่อคุณมีโมเดลซับซ้อนที่มีตัวแปรคั่นกลางหลายตัว | n > 100 |
การเปรียบเทียบวิธีการทดสอบการคั่นกลางกับข้อกำหนดขนาดตัวอย่าง
สรุป: ถ้าคุณมีข้อมูลดิบ ใช้ bootstrapping เสมอ Sobel test ล้าสมัยและยอมรับได้เฉพาะเมื่อวิธี bootstrap ไม่พร้อมใช้งาน
ควรใช้ Bootstrap Samples กี่ตัว?
PROCESS มีค่าเริ่มต้น 5,000 bootstrap samples เพียงพอหรือไม่?
| Bootstrap Samples | ความแม่นยำ | คำแนะนำ |
|---|---|---|
| 1,000 | ยอมรับได้ | ต่ำสุดสำหรับการวิเคราะห์เชิงสำรวจ |
| 5,000 | ดี | มาตรฐานสำหรับการวิจัยส่วนใหญ่ (ค่าเริ่มต้น PROCESS) |
| 10,000 | ยอดเยี่ยม | ดีที่สุดสำหรับการตีพิมพ์ในวารสารชั้นนำ |
คำแนะนำสำหรับขนาด bootstrap sample สำหรับการวิเคราะห์ตัวแปรคั่นกลาง
คำแนะนำ: ใช้ 5,000 สำหรับการวิจัยส่วนใหญ่ เพิ่มเป็น 10,000 ถ้าคุณมีตัวอย่างขนาดเล็ก (n < 100) หรือถ้าคุณกำลังส่งไปยังวารสารชั้นนำ
หมายเหตุการคำนวณ: bootstrap samples มากขึ้น = เวลาคำนวณนานขึ้น บนคอมพิวเตอร์สมัยใหม่ 5,000 samples ใช้เวลา 5-10 วินาที ในขณะที่ 10,000 ใช้เวลา 10-20 วินาที การลงทุนเวลาเล็กน้อยนี้คุ้มค่าสำหรับผลลัพธ์ที่แม่นยำขึ้น
เปรียบเทียบสองวิธี
| คุณสมบัติ | Baron & Kenny | PROCESS Macro |
|---|---|---|
| ความง่ายในการใช้ | ต้องการการถดถอย 3 ครั้งแยกกัน | คำสั่งเดียว |
| การทดสอบผลกระทบทางอ้อม | Sobel test (สมมติการแจกแจงปกติ) | Bootstrap CI (ไม่มีสมมติฐาน) |
| พลังทางสถิติ | ต่ำกว่า | สูงกว่า |
| มาตรฐานสมัยใหม่ | ล้าสมัย | แนวปฏิบัติที่ดีที่สุดในปัจจุบัน |
| ช่วงความเชื่อมั่น | ไม่ให้ | ให้ Bootstrap CI |
| คำแนะนำ | ใช้สำหรับการเรียนรู้ | ใช้สำหรับงานวิจัย |
การเปรียบเทียบแนวทาง Baron & Kenny และ PROCESS Macro สำหรับการวิเคราะห์ตัวแปรคั่นกลาง
ทั้งสองวิธีให้ผลลัพธ์ที่คล้ายกันในตัวอย่างของเรา:
- Baron & Kenny: Indirect effect = 0.303 (Sobel test)
- PROCESS: Indirect effect = 0.303 (Bootstrap CI)
การรายงานผลลัพธ์การวิเคราะห์ตัวแปรคั่นกลาง
เมื่อรายงานการวิเคราะห์ตัวแปรคั่นกลางในวิทยานิพนธ์หรือบทความวิจัยของคุณ ให้รวม:
- สถิติเชิงพรรณนา สำหรับตัวแปรทั้งหมด (ค่าเฉลี่ย, SDs, ความสัมพันธ์)
- ค่าสัมประสิทธิ์เส้นทาง สำหรับ a, b, c และ c'
- ระดับนัยสำคัญ สำหรับแต่ละเส้นทาง
- ขนาดผลกระทบทางอ้อม พร้อมช่วงความเชื่อมั่น 95%
- ประเภทของการคั่นกลาง (เต็มหรือบางส่วน)
- แผนภาพ ที่แสดงโมเดลการคั่นกลางพร้อมค่าสัมประสิทธิ์
ตัวอย่างการแถลงผลลัพธ์:
"การวิเคราะห์ตัวแปรคั่นกลางโดยใช้ PROCESS Model 4 (5,000 bootstrap samples) แสดงให้เห็นว่า Discount (M) เป็นตัวแปรคั่นกลางความสัมพันธ์ระหว่าง Relationship (X) และ Satisfaction (Y) อย่างมีนัยสำคัญ ผลกระทบทางอ้อมมีนัยสำคัญ ab = 0.30, 95% CI [0.12, 0.54] ผลกระทบทางตรงของ Relationship ต่อ Satisfaction ยังคงมีนัยสำคัญเมื่อควบคุม Discount (c' = 0.17, p < .001) บ่งชี้ partial mediation Relationship ทำนาย Discount อย่างมีนัยสำคัญ (a = 0.41, p < .001) และ Discount ทำนาย Satisfaction อย่างมีนัยสำคัญ (b = 0.73, p < .001)"
ตารางผลลัพธ์การคั่นกลางในรูปแบบ APA
ใช้แม่แบบนี้เพื่อรายงานผลลัพธ์การคั่นกลางของคุณในรูปแบบ APA แทนที่ค่าด้วยค่าสัมประสิทธิ์จริงของคุณ:
| เส้นทาง | ค่าสัมประสิทธิ์ | SE | t | p | 95% CI |
|---|---|---|---|---|---|
| ผลกระทบรวม (c) | 0.47 | 0.07 | 7.25 | < .001 | [0.34, 0.60] |
| ผลกระทบทางตรง (c') | 0.17 | 0.03 | 6.02 | < .001 | [0.11, 0.23] |
| Path a (X → M) | 0.41 | 0.08 | 4.94 | < .001 | [0.24, 0.58] |
| Path b (M → Y) | 0.73 | 0.04 | 17.24 | < .001 | [0.65, 0.82] |
| ผลกระทบทางอ้อม (ab) | 0.30 | 0.11* | — | — | [0.12, 0.54] |
หมายเหตุ. N = 40. Bootstrap samples = 5,000. *SE สำหรับผลกระทบทางอ้อมเป็น bootstrap standard error. CI = ช่วงความเชื่อมั่น
หัวข้อตาราง: "ผลลัพธ์การวิเคราะห์ตัวแปรคั่นกลางแสดงผลกระทบของคุณภาพความสัมพันธ์ (X) ต่อความพึงพอใจของลูกค้า (Y) ผ่านส่วนลดส่วนบุคคล (M)"
เวอร์ชันคัดลอกวางสำหรับ Microsoft Word:
คัดลอกข้อความด้านล่างและวางใน Word จากนั้นใช้ ตาราง → แปลง → ข้อความเป็นตาราง เพื่อสร้างตารางที่จัดรูปแบบ
เส้นทาง ค่าสัมประสิทธิ์ SE t p 95% CI
ผลกระทบรวม (c) 0.47 0.07 7.25 < .001 [0.34, 0.60]
ผลกระทบทางตรง (c') 0.17 0.03 6.02 < .001 [0.11, 0.23]
Path a (X → M) 0.41 0.08 4.94 < .001 [0.24, 0.58]
Path b (M → Y) 0.73 0.04 17.24 < .001 [0.65, 0.82]
ผลกระทบทางอ้อม (ab) 0.30 0.11* — — [0.12, 0.54]
หมายเหตุ: *SE สำหรับผลกระทบทางอ้อมเป็น bootstrap standard error จาก 5,000 samples
ข้อสมมติของการวิเคราะห์ตัวแปรคั่นกลาง
เช่นเดียวกับวิธีทางสถิติทั้งหมด การวิเคราะห์ตัวแปรคั่นกลางต้องอาศัยข้อสมมติหลักหลายข้อ การละเมิดข้อสมมติเหล่านี้อาจนำไปสู่การประมาณผลกระทบทางอ้อมที่มีอคติ
1. ความเป็นเส้นตรง (Linearity)
ข้อสมมติ: ความสัมพันธ์ระหว่าง X→M, M→Y และ X→Y ต้องเป็นเส้นตรง
วิธีทดสอบ: สร้างกราฟการกระจายสำหรับแต่ละความสัมพันธ์ มองหารูปแบบเส้นโค้ง ถ้าความสัมพันธ์เป็นเส้นโค้ง ให้พิจารณา:
- การแปลงตัวแปร (logarithm, square root หรือ polynomial terms)
- ใช้โมเดลการคั่นกลางแบบไม่เชิงเส้น (มีใน R packages เช่น
mediation)
จะเกิดอะไรขึ้นถ้าละเมิด: ผลกระทบทางอ้อมจะถูกประมาณต่ำเกินไปถ้าความสัมพันธ์ที่แท้จริงเป็นเส้นโค้ง
2. ไม่มีตัวแปรกวนที่ไม่ได้วัด (No Unmeasured Confounding)
ข้อสมมติ: ไม่มีตัวแปรที่ถูกละเว้นซึ่งมีผลต่อทั้ง M และ Y (หรือทั้ง X และ M)
วิธีทดสอบ: ข้อสมมตินี้ไม่สามารถทดสอบทางสถิติได้ คุณต้องพึ่งพา:
- ความรู้ทางทฤษฎี ในสาขาวิจัยของคุณ
- รวมตัวแปรควบคุม ที่อาจสร้างความสับสนในความสัมพันธ์
- การวิเคราะห์ความไว เพื่อประเมินว่าผลลัพธ์ของคุณแข็งแกร่งเพียงใดต่อตัวแปรกวนที่เป็นไปได้
จะเกิดอะไรขึ้นถ้าละเมิด: การประมาณผลกระทบทางอ้อมจะมีอคติ ถ้าตัวแปรที่ไม่ได้วัดทำให้เกิดทั้ง M และ Y คุณอาจพบการคั่นกลางเทียม
3. ลำดับเวลา (Temporal Precedence)
ข้อสมมติ: X ต้องเกิดก่อน M และ M ต้องเกิดก่อน Y
วิธีรับประกัน: ใช้:
- ข้อมูลตามยาว (วัด X ที่เวลา 1, M ที่เวลา 2, Y ที่เวลา 3)
- การออกแบบการทดลอง ด้วยการสุ่มไปที่ X
- ข้อมูลภาคตัดขวางพร้อมทฤษฎีที่แข็งแกร่ง (เฉพาะเมื่อข้อมูลตามยาวไม่สามารถทำได้)
จะเกิดอะไรขึ้นถ้าละเมิด: คุณไม่สามารถอ้างเหตุและผลได้ การคั่นกลางภาคตัดขวางสามารถแสดงเฉพาะรูปแบบทางสถิติ ไม่ใช่กลไกเชิงสาเหตุ
4. ไม่มีความคลาดเคลื่อนในการวัด (No Measurement Error)
ข้อสมมติ: X, M และ Y ถูกวัดโดยไม่มีความคลาดเคลื่อน (หรือความคลาดเคลื่อนในการวัดน้อยที่สุด)
วิธีทดสอบ: คำนวณความเชื่อถือได้ (Cronbach's alpha สำหรับมาตรวัด) ตั้งเป้าที่ α > 0.70
จะเกิดอะไรขึ้นถ้าละเมิด: ความคลาดเคลื่อนในการวัดใน M ทำให้ผลกระทบทางอ้อมมีอคติลง (attenuation bias) หมายความว่าคุณมีแนวโน้มที่จะพลาดผลกระทบการคั่นกลางที่แท้จริง
วิธีแก้: ใช้การคั่นกลางตัวแปรแฝง (structural equation modeling) ซึ่งแก้ไขความคลาดเคลื่อนในการวัด
5. ความเป็นอิสระของการสังเกต (Independence of Observations)
ข้อสมมติ: ข้อมูลของผู้เข้าร่วมแต่ละคนเป็นอิสระ (ไม่มีการจัดกลุ่มหรือซ้อน)
จะเกิดอะไรขึ้นถ้าละเมิด: ถ้าผู้เข้าร่วมถูกซ้อน (เช่น นักเรียนในโรงเรียน) ความคลาดเคลื่อนมาตรฐานจะเล็กเกินไป นำไปสู่นัยสำคัญที่พองตัว
วิธีแก้: ใช้โมเดลการคั่นกลางแบบหลายระดับถ้าข้อมูลมีการจัดกลุ่ม
6. ไม่มีปฏิสัมพันธ์ X × M (No X × M Interaction)
ข้อสมมติ: ผลกระทบของ M ต่อ Y ไม่ขึ้นอยู่กับระดับของ X
วิธีทดสอบ: เพิ่มเทอมปฏิสัมพันธ์ X × M ในโมเดลการถดถอยของคุณที่ทำนาย Y ถ้ามีนัยสำคัญ คุณมี moderated mediation ไม่ใช่การคั่นกลางธรรมดา
จะเกิดอะไรขึ้นถ้าละเมิด: ผลกระทบทางอ้อมแตกต่างกันในระดับของ X คุณต้องใช้ PROCESS Model 7, 8 หรือ 14 (moderated mediation models)
การคั่นกลาง vs. การกำกับ: อย่าสับสนการคั่นกลางกับการกำกับ ในการคั่นกลาง M ถ่ายทอดผลกระทบของ X ต่อ Y ในการกำกับ M เปลี่ยนความแข็งแรงของความสัมพันธ์ X-Y เรียนรู้เพิ่มเติม: Moderator vs Mediator
การแก้ไขปัญหาทั่วไป
ข้อผิดพลาด "PROCESS command not found"
ปัญหา: เมื่อคุณรัน PROCESS, SPSS บอกว่าคำสั่งไม่มีอยู่
วิธีแก้:
- ตรวจสอบการติดตั้ง: ไปที่
Analyze→Regressionและตรวจสอบว่าPROCESS v5.0 by Andrew F. Hayesปรากฏในเมนู - ติดตั้ง PROCESS ใหม่: ดาวน์โหลดเวอร์ชันล่าสุดจาก processmacro.org และทำตามคำแนะนำการติดตั้ง
- ตรวจสอบ syntax: ถ้ารัน PROCESS ผ่าน syntax ให้แน่ใจว่าคุณใช้รูปแบบคำสั่งที่ถูกต้องสำหรับ v5.0 (syntax เปลี่ยนจาก v4.x)
- รีสตาร์ท SPSS: บางครั้ง SPSS ต้องการรีสตาร์ทหลังการติดตั้งเพื่อให้ PROCESS ปรากฏ
ช่วงความเชื่อมั่น Bootstrap รวมศูนย์
ปัญหา: ผลกระทบทางอ้อมของคุณไม่มีนัยสำคัญเพราะ CI bootstrap รวมศูนย์ (เช่น [-0.05, 0.23])
ความหมาย: ไม่มีหลักฐานเพียงพอสำหรับการคั่นกลาง ผลกระทบทางอ้อมอาจเป็นศูนย์ได้
วิธีแก้:
- ตรวจสอบทฤษฎีของคุณ: การคั่นกลางมีความเป็นไปได้ทางทฤษฎีหรือไม่? บางทีการกำกับหรือกลไกอื่นกำลังทำงาน
- เพิ่มขนาดตัวอย่าง: ตัวอย่างขนาดเล็ก (n < 100) มีกำลังต่ำในการตรวจจับการคั่นกลาง ตั้งเป้าที่ n > 200
- ปรับปรุงการวัด: ความเชื่อถือต่ำ (Cronbach's α < 0.70) ลดทอนผลกระทบการคั่นกลาง ใช้มาตรวัดที่ผ่านการตรวจสอบ
- ตรวจสอบการปราบปราม: ดูที่เครื่องหมายของ Path a และ Path b ถ้ามีเครื่องหมายตรงข้าม คุณอาจมี inconsistent mediation
เส้นทางทั้งหมดมีนัยสำคัญแต่ผลกระทบทางอ้อมไม่มี
ปัญหา: Path a มีนัยสำคัญ Path b มีนัยสำคัญ แต่ CI bootstrap สำหรับ ab รวมศูนย์
ทำไมเกิดขึ้น: ผลคูณ a × b อาจไม่มีนัยสำคัญแม้ว่าทั้งสองเส้นทางมีนัยสำคัญแยกกัน สิ่งนี้เกิดขึ้นเมื่อ:
- ขนาดผลกระทบเล็ก: ทั้งสองเส้นทางอ่อน (เช่น a = 0.15, b = 0.18) ทำให้ผลคูณยิ่งเล็กลง (ab = 0.027)
- ความแปรปรวนสูง: หนึ่งหรือทั้งสองเส้นทางมีความคลาดเคลื่อนมาตรฐานใหญ่
- ขนาดตัวอย่างไม่เพียงพอ: คุณต้องการข้อมูลมากขึ้นเพื่อตรวจจับผลกระทบทางอ้อม
วิธีแก้:
- เพิ่ม bootstrap samples: ลอง 10,000 samples สำหรับการประมาณ CI ที่แม่นยำยิ่งขึ้น
- ตรวจสอบความคลาดเคลื่อนในการวัด: ตัวแปรที่ไม่เชื่อถือลดทอนผลกระทบทางอ้อม
- เพิ่มขนาดตัวอย่าง: นี่มักเป็นปัญหาหลัก — ตั้งเป้าที่ n > 200
PROCESS ใช้เวลานานเกินไปในการรัน
ปัญหา: PROCESS กำลังรันหลายนาทีหรือดูเหมือนค้าง
สาเหตุ:
- bootstrap samples มากเกินไป: ถ้าคุณตั้ง bootstrap > 50,000 จะใช้เวลานาน
- ชุดข้อมูลขนาดใหญ่: PROCESS ช้าลงด้วยชุดข้อมูลขนาดใหญ่มาก (n > 10,000)
- โมเดลซับซ้อน: โมเดลที่มีตัวแปรคั่นกลาง/กำกับหลายตัวใช้เวลานานกว่า
วิธีแก้:
- ลด bootstrap samples: 5,000 เพียงพอสำหรับการวิจัยส่วนใหญ่ ใช้ 10,000 เฉพาะสำหรับการตีพิมพ์
- ใช้ตัวอย่างสุ่ม: ถ้า n > 5,000 วิเคราะห์ชุดย่อยสุ่ม (n = 1,000-2,000) เพื่อทดสอบโมเดลของคุณก่อน
- ตรวจสอบลูปไม่สิ้นสุด: ถ้า PROCESS ค้างจริงๆ (> 10 นาที) บังคับปิดและรีสตาร์ท SPSS
ผลกระทบทางอ้อมเป็นลบแต่ฉันคาดว่าจะเป็นบวก
ปัญหา: โมเดลทางทฤษฎีของคุณทำนายการคั่นกลางเชิงบวก แต่คุณได้ผลกระทบทางอ้อมเชิงลบ
ความหมาย: คุณมี inconsistent mediation (suppression) ตัวแปรคั่นกลางทำงานตรงข้ามกับผลกระทบทางตรงแทนที่จะถ่ายทอดมัน
คำอธิบายที่เป็นไปได้:
- ทฤษฎีผิด: กลไกสมมติฐานของคุณไม่ถูกต้อง
- เครื่องหมายตรงข้าม: ตรวจสอบว่า Path a และ Path b มีเครื่องหมายตรงข้าม (หนึ่งบวก หนึ่งลบ)
- ตัวแปรที่สาม: ตัวแปรกวนที่ไม่ได้วัดอาจสร้างความสัมพันธ์เทียม
ขั้นตอนต่อไป:
- รายงานอย่างซื่อสัตย์: ผลกระทบทางอ้อมเชิงลบเป็นผลการค้นพบทางวิทยาศาสตร์ที่ถูกต้อง
- แก้ไขทฤษฎีของคุณ: อธิบายว่าทำไมตัวแปรคั่นกลางปราบปรามแทนที่จะถ่ายทอดผลกระทบ
- สำรวจทางเลือก: พิจารณาว่าคุณกำลังวัดตัวแปรคั่นกลางที่ถูกต้องหรือไม่
Path c' กลายเป็นไม่มีนัยสำคัญแต่ CI Bootstrap รวมศูนย์
ปัญหา: ผลกระทบทางตรง (c') กลายเป็นไม่มีนัยสำคัญหลังรวมตัวแปรคั่นกลาง แต่ผลกระทบทางอ้อมไม่มีนัยสำคัญ (CI รวมศูนย์)
ความหมาย: ทั้งผลกระทบทางตรงและทางอ้อมไม่มีนัยสำคัญ นี่แนะนำว่า:
- ความสัมพันธ์เดิม X→Y อาจเป็นความสัมพันธ์เทียม
- ขนาดตัวอย่างไม่เพียงพอ
- ตัวแปรคั่นกลางไม่ใช่ตัวที่ถูกต้อง
วิธีแก้:
- เพิ่มขนาดตัวอย่าง: คุณต้องการกำลังมากขึ้นเพื่อตรวจจับผลกระทบเล็ก
- พิจารณาทฤษฎีใหม่: บางทีความสัมพันธ์ X→Y เกิดจากปัจจัยที่สาม
- ทดสอบตัวแปรคั่นกลางทางเลือก: กลไกสมมติฐานของคุณอาจผิด
Output PROCESS แสดงค่าแปลก (NaN, Inf)
ปัญหา: Output PROCESS แสดง NaN (Not a Number) หรือ Inf (infinity) สำหรับค่าสัมประสิทธิ์บางตัว
สาเหตุ:
- Multicollinearity: X และ M มีความสัมพันธ์แน่นมาก (r > 0.90)
- ความแปรปรวนศูนย์: หนึ่งในตัวแปรไม่มีความแปรปรวน (ผู้เข้าร่วมทุกคนมีค่าเดียวกัน)
- ค่าที่หายไป: ค่าที่หายไปมากเกินไปในข้อมูล
วิธีแก้:
- ตรวจสอบความสัมพันธ์: รัน
Analyze→Correlate→Bivariateเพื่อตรวจสอบ multicollinearity - ตรวจสอบค่าพรรณนา: แน่ใจว่าตัวแปรทั้งหมดมีความแปรปรวน (SD > 0)
- จัดการค่าที่หายไป: ตัดกรณีที่มีข้อมูลหายไปหรือใช้การ imputation
คำถามที่พบบ่อย
สรุป
คุณได้เรียนรู้สองวิธีในการรันการวิเคราะห์ตัวแปรคั่นกลางใน SPSS:
- แนวทาง Baron & Kenny: วิธีคลาสสิก 3 ขั้นตอนโดยใช้การถดถอยแยกกัน (ดีสำหรับการเรียนรู้ตรรกะ)
- PROCESS Macro: วิธีสมัยใหม่พร้อมช่วงความเชื่อมั่น bootstrapped (ดีที่สุดสำหรับงานวิจัยจริง)
สำหรับวิทยานิพนธ์หรือโครงการวิจัยของคุณ เราแนะนำ PROCESS Model 4 เพราะให้ผลลัพธ์ที่แม่นยำและน่าเชื่อถือมากขึ้นผ่าน bootstrapping
จำไว้ว่า: การวิเคราะห์ตัวแปรคั่นกลางเปิดเผยกลไก แต่ไม่ได้พิสูจน์เหตุและผล ตีความผลลัพธ์ของคุณภายในบริบทของการออกแบบการวิจัยและกรอบทฤษฎีของคุณเสมอ
ขั้นตอนถัดไป:
- ดาวน์โหลดชุดข้อมูลตัวอย่างของเรา (มีใน sidebar) และรันทั้งสองวิธีด้วยตัวคุณเองเพื่อเสริมการเรียนรู้ของคุณ
- เรียนรู้การวิเคราะห์ตัวแปรกำกับเพื่อทดสอบว่าความสัมพันธ์เกิดขึ้นเมื่อใด: ตัวแปรกำกับ คือ อะไร? วิธีการวิเคราะห์ตัวแปรกำกับใน SPSS
- ทำความเข้าใจพื้นฐาน Linear Regression: Linear Regression คืออะไร? วิธีการวิเคราะห์ใน SPSS
- สำรวจเทคนิคขั้นสูง: วิธีการวิเคราะห์ตัวแปรคั่นกลางใน R
เอกสารอ้างอิง
Baron, R. M., & Kenny, D. A. (1986). The moderator-mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology, 51(6), 1173-1182.
Fritz, M. S., & MacKinnon, D. P. (2007). Required sample size to detect the mediated effect. Psychological Science, 18(3), 233-239.
Hayes, A. F. (2009). Beyond Baron and Kenny: Statistical mediation analysis in the new millennium. Communication Monographs, 76(4), 408-420.
Hayes, A. F. (2022). Introduction to mediation, moderation, and conditional process analysis: A regression-based approach (3rd ed.). New York: Guilford Press.
Kenny, D. A. (2018). Mediation. Retrieved from http://davidakenny.net/cm/mediate.htm
Shrout, P. E., & Bolger, N. (2002). Mediation in experimental and nonexperimental studies: New procedures and recommendations. Psychological Methods, 7(4), 422-445.
Sobel, M. E. (1982). Asymptotic intervals for indirect effects in structural equations models. In S. Leinhart (Ed.), Sociological methodology 1982 (pp. 290-312). San Francisco: Jossey-Bass.