Linearitatea în statistică descrie relațiile în care o schimbare într-o variabilă corespunde direct unei schimbări într-o altă variabilă. În acest articol, vom explora ce înseamnă linearitatea, cum să testezi linearitatea și vom discuta importanța sa în analiza de regresie, corelație și alte metode statistice.
Elementele de Bază: Ce Este Linearitatea în Statistică?
Linearitatea în statistică se referă la relații. Dar nu orice fel de relații, ci cele în care o schimbare într-o variabilă corespunde direct unei schimbări într-o altă variabilă. Imaginează-ți o linie dreaptă care conectează două puncte pe un grafic. Aceasta este o relație liniară în acțiune: cu cât linia este mai dreaptă, cu atât relația dintre variabile este mai "liniară".
Un exemplu simplu de relație liniară este conexiunea dintre distanța pe care o parcurgi și timpul necesar pentru a ajunge acolo. Dacă călătorești cu viteză constantă, relația dintre distanță și timp va fi liniară, ceea ce înseamnă că dacă dublezi timpul, vei dubla și distanța.
Când avem de-a face cu linearitatea în statistică, reprezentăm adesea relația dintre variabile folosind o ecuație liniară. În cazul cel mai simplu, care implică două variabile (x și y), relația liniară poate fi reprezentată prin ecuația:
Aici, reprezintă panta (rata de schimbare) a liniei, este interceptul y (valoarea lui y când ), iar și sunt variabilele independentă și dependentă. Poți considera panta ca fiind "înclinarea" liniei, în timp ce interceptul y este locul în care linia intersectează axa y.
Să explorăm un exemplu. Să presupunem că vrei să prezici prețul unei pizza pe baza dimensiunii sale (în inchi). Aduni câteva date și descoperi că relația dintre dimensiune () și preț () este liniară, cu o pantă () de 2 și un intercept y () de 5. Ecuația ta liniară ar arăta astfel:
Acum, dacă vrei să afli prețul unei pizza de 12 inchi, înlocuiește valoarea pentru :
Deci, o pizza de 12 inchi ar costa 29$.
De Ce Ar Trebui Să Ne Pese de Linearitate?
Linearitatea este coloana vertebrală a multor tehnici statistice care ne ajută să înțelegem tendințe, modele și relații între variabile. Este vitală în domenii precum științele sociale, economie și științele naturale. Să explorăm câteva dintre motivele pentru care linearitatea este atât de importantă:
1. Analiza de Regresie
Una dintre cele mai comune utilizări ale linearității este în analiza de regresie. Analiza de regresie se ocupă cu găsirea unui model matematic care se potrivește cel mai bine unui set de puncte de date. Când există o relație liniară între variabile, putem folosi o tehnică numită regresie liniară pentru a găsi linia care se potrivește cel mai bine.
Dacă presupunem că există o relație liniară între variabile, dar nu există, este posibil să nu obținem rezultate precise. Am putea ajunge cu un model care nu descrie comportamentul variabilelor care ne interesează sau am putea face predicții care sunt semnificativ greșite.
De exemplu, să presupunem că investigăm cum afectează temperatura creșterea plantelor. Presupunem că există o relație liniară între temperatură și creștere, așa că folosim regresia liniară pentru a face predicții. Dar dacă relația dintre temperatură și creștere este neliniară (poate există o temperatură optimă unde creșterea este maximă, formând o relație curbă), atunci modelul nostru de regresie liniară ar putea să nu fie precis. Am putea face predicții care nu reflectă rezultatele din lumea reală.
De aceea este important să testăm linearitatea înainte de a efectua regresia liniară. Trebuie să verificăm că relația dintre variabile este liniară înainte de a presupune că este. Dacă nu există o relație liniară, ar putea fi nevoie să transformăm datele sau să folosim un model diferit pentru a capta cu acuratețe comportamentul variabilelor.
Prin testarea linearității în regresie, putem fi siguri că rezultatele noastre de regresie liniară reflectă cu acuratețe relația dintre variabilele care ne interesează.
2. Corelația
Un alt motiv pentru a ne păsa de linearitate este că este crucială pentru înțelegerea corelației. Corelația este o măsură a cât de puternic sunt legate două variabile. Când relația dintre variabile este liniară, coeficientul de corelație (de obicei reprezentat de "r" sau "rho") ne poate oferi informații valoroase despre puterea și direcția relației.
Un coeficient de corelație de +1 indică o relație liniară pozitivă perfectă, în timp ce un coeficient de corelație de -1 semnifică o relație liniară negativă perfectă. Un coeficient de corelație de 0 ar indica lipsa unei relații liniare.
De exemplu, să presupunem că vrei să știi dacă există o relație între numărul de ore pe care studenții le studiază și scorurile lor la examene. Prin calcularea coeficientului de corelație, poți determina puterea și direcția relației liniare dintre aceste două variabile.
3. Analiza Covarianței (ANCOVA) și Modelele Mixte
În timp ce ANOVA standard nu necesită asumpții de linearitate (deoarece compară medii între grupuri categorice), linearitatea devine critică când extindem ANOVA la modele mai complexe, cum ar fi ANCOVA (Analiza Covarianței) sau când includem covariate continue.
În ANCOVA, examinăm diferențele dintre grupuri în timp ce controlăm pentru covariate continue. Asumpția de linearitate afirmă că relația dintre covariată și variabila dependentă trebuie să fie liniară pentru toate grupurile comparate.
De exemplu, să presupunem că comparăm scorurile de test ale trei metode de predare (A, B și C) în timp ce controlăm pentru scorurile de cunoștințe prealabile ale studenților. Trebuie să ne asigurăm că relația dintre cunoștințele prealabile și scorurile de test este liniară pentru toate cele trei grupuri de metode de predare.
Dacă relația dintre covariată și variabila dependentă este neliniară (poate curbă sau arătând modele diferite între grupuri), atunci rezultatele ANCOVA pot fi deplasate. Mediile ajustate ar fi estimate incorect, putând duce la concluzii false despre diferențele dintre grupuri.
Când linearitatea este încălcată în ANCOVA, avem mai multe opțiuni: să transformăm covariata pentru a obține linearitate, să folosim termeni polinomiali pentru a modela relații neliniare sau să folosim abordări analitice alternative, cum ar fi metodele neparametrice. Prin verificarea linearității înainte de a efectua ANCOVA, ne asigurăm că rezultatele noastre reflectă cu acuratețe diferențele reale dintre grupuri după contabilizarea covariatelor.
4. Testarea Ipotezelor
În statistică, testarea ipotezelor este o metodă de a determina dacă două variabile sunt legate. De obicei, începem prin a presupune că nu există nicio relație între variabilele pe care le examinăm (aceasta se numește ipoteza nulă). Apoi, colectăm date și efectuăm calcule pentru a determina dacă există suficiente dovezi pentru a respinge ipoteza nulă și a concluziona că există o relație între variabile.
Cu toate acestea, dacă presupunem că există o relație liniară între variabile când nu există, am putea ajunge să respingem ipoteza nulă când nu ar trebui. Aici intervine linearitatea. Trebuie să verificăm că există de fapt o relație liniară între variabilele pe care le testăm înainte de a efectua testarea ipotezelor.
De exemplu, să presupunem că testăm dacă există o relație între numărul de ore în care cineva face exerciții pe săptămână și nivelurile sale de colesterol. Dacă există o relație liniară între aceste variabile, putem folosi testarea ipotezelor pentru a determina dacă există suficiente dovezi pentru a concluziona că exercițiile mai multe duc la niveluri mai scăzute de colesterol.
Dar dacă relația dintre exerciții și colesterol este neliniară (poate curbă sau arătând randamente descrescătoare), atunci testarea noastră de ipoteze ar putea să nu fie precisă. Am putea ajunge să respingem ipoteza nulă și să concluzionăm că există o relație între variabile când relația nu urmează modelul liniar pe care l-am presupus.
5. Proiectarea Experimentelor
În statistică, proiectarea experimentală ne ajută să determinăm cum diferite variabile afectează un rezultat. De exemplu, dacă investigăm ce factori afectează creșterea plantelor, am putea manipula variabile precum lumina, apa și îngrășământul pentru a observa efectele lor asupra plantelor.
În multe proiecte experimentale, presupunem că efectul fiecărei variabile asupra rezultatului este liniar. Aici intervine linearitatea. Trebuie să verificăm că relația dintre variabile și rezultat este liniară înainte de a proiecta experimentul nostru.
Dacă presupunem că există o relație liniară între o variabilă și rezultat când nu există, este posibil să nu obținem rezultatele pe care le căutăm. Am putea manipula variabila și să nu observăm niciun efect asupra rezultatului sau am putea vedea un efect care diferă de ceea ce ne-am așteptat.
De exemplu, să presupunem că investigăm cum diferite niveluri de lumină afectează creșterea plantelor. Presupunem că există o relație liniară între lumină și creștere, așa că proiectăm experimentul nostru pentru a testa diferite niveluri de lumină. Dar dacă relația dintre lumină și creștere este neliniară (poate creșterea se plafonează după un anumit prag), atunci experimentul nostru ar putea să nu fie precis. Am putea manipula lumina și să nu observăm niciun efect suplimentar asupra creșterii sau am putea vedea un model diferit decât cel așteptat.
Testarea linearității înainte de proiectarea unui experiment este crucială. Trebuie să verificăm că efectul fiecărei variabile asupra rezultatului este liniar înainte de a presupune că este. Dacă nu există o relație liniară, ar putea fi nevoie să folosim o proiectare experimentală sau un model diferit pentru a capta cu acuratețe comportamentul variabilelor.
Ce Se Întâmplă Când Linearitatea Este Încălcată?
Este crucial să verificăm că avem o relație liniară înainte de a folosi un model de regresie liniară. Dacă nu o facem, predicțiile noastre vor fi inexacte și este posibil să nu obținem rezultatele pe care le căutăm. Încălcarea asumpției de linearitate ar putea chiar să ne conducă la identificarea relațiilor unde nu există. De aceea trebuie să testăm linearitatea înainte de a face predicții.
Dacă încălcăm asumpția de linearitate, putem obține rezultate serios deplasate. De exemplu, dacă încercăm să prezicem prețurile caselor pe baza suprafeței, am putea presupune că putem folosi un model liniar. Dar dacă relația dintre prețurile caselor și suprafață nu este liniară (poate prețurile cresc exponențial pe măsură ce suprafața crește), atunci modelul nostru de regresie liniară va produce predicții inexacte.
De aceea este esențial să testăm întotdeauna linearitatea înainte de a folosi un model de regresie liniară. Dacă nu o facem, am putea ajunge cu predicții deplasate, estimări incorecte ale coeficienților sau rezultate înșelătoare în general. Luând timpul pentru a verifica linearitatea, putem asigura că modelele noastre reflectă cu acuratețe relațiile din lumea reală și oferă informații valide despre fenomenele pe care le investigăm.
Cum Să Testezi Linearitatea în Statistică?
Înțelegând că linearitatea este importantă, cum o testăm de fapt? Există mai multe metode pe care le putem folosi:
1. Scatterplot-uri
Un scatterplot este un grafic care afișează relația dintre două variabile. Dacă există o relație liniară, punctele de pe scatterplot vor forma un model care se apropie de o linie dreaptă.
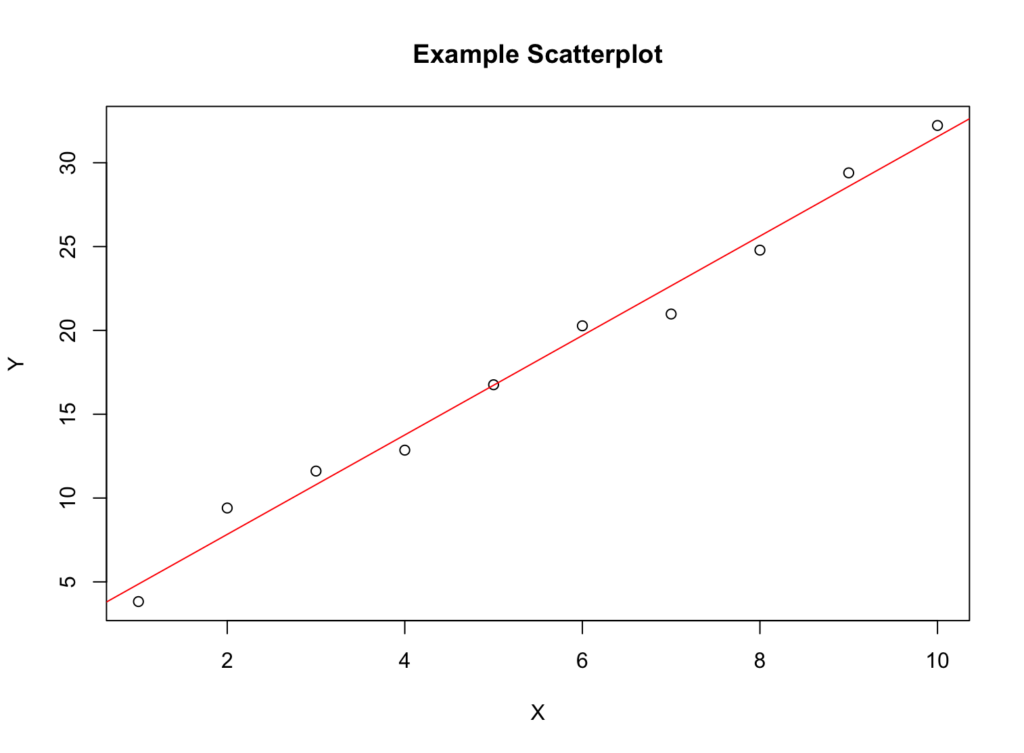
Figura 1: Exemplu de scatterplot demonstrând relația liniară
2. Coeficientul de Corelație
Coeficientul de corelație măsoară puterea și direcția relației liniare dintre două variabile. Dacă există o relație liniară, coeficientul de corelație va fi aproape de 1 (sau -1 pentru o relație negativă). De exemplu, un coeficient de corelație de 0.9975 indică o relație liniară pozitivă foarte puternică între variabile.
3. Grafice de Reziduuri
Un grafic de reziduuri arată diferența dintre valorile observate și valorile prezise din modelul nostru de regresie. Dacă există o dispersie aleatoare de puncte fără un model discernibil, asumpția de linearitate este probabil îndeplinită. Cu toate acestea, dacă există un model (cum ar fi o curbă sau o formă de pâlnie), modelul nostru liniar ar putea să nu fie potrivit.
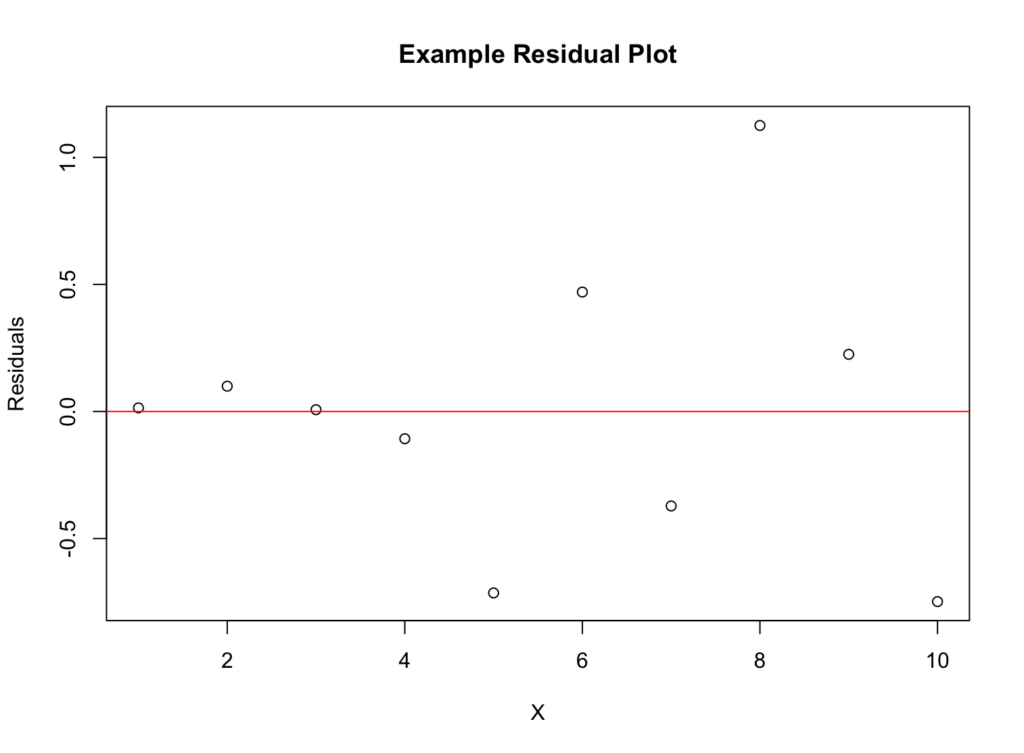
Figura 2: Grafic de reziduuri pentru evaluarea linearității
Prin utilizarea acestor metode de diagnostic, putem determina dacă există o relație liniară între două variabile. Dacă există, putem folosi un model de regresie liniară pentru a face predicții. Dacă nu există, va trebui fie să transformăm datele noastre pentru a obține linearitate, fie să folosim o abordare diferită de modelare (cum ar fi regresia polinomială sau modele neliniare).
Întrebări Frecvente
Concluzie
În rezumat, linearitatea este un concept fundamental în statistică. Fie că efectuezi analiza de regresie liniară, efectuezi ANCOVA sau testezi ipoteze, trebuie să verifici că există o relație liniară între variabilele pe care le examinezi.
Prin testarea linearității folosind scatterplot-uri, coeficienți de corelație și grafice de reziduuri, poți evita rezultatele deplasate și te poți asigura că concluziile tale statistice sunt valide. Înțelegerea a ce înseamnă linearitatea și cum să testezi linearitatea sunt abilități esențiale pentru orice analist de date sau cercetător care lucrează cu date cantitative. Amintește-ți să evaluezi întotdeauna asumpțiile de linearitate înainte de a aplica modele liniare datelor tale.