Ce Este o Măsură de Tendință Centrală? Media, Mediana, Modul [Ghid]

O măsură de tendință centrală este un concept statistic fundamental care te ajută să înțelegi valoarea tipică sau centrală într-un set de date. În acest ghid, vei învăța cele trei măsuri principale (media, mediana și modul), cum să calculezi fiecare și când să le folosești în analiza ta statistică.

Obiective de Învățare

Până la sfârșitul acestui articol, ar trebui să poți:

Înțelege conceptul de măsuri de tendință centrală și importanța lor în statistică și analiza datelor.
Defini și diferenția între medie, mediană și mod ca măsuri de tendință centrală.
Explica formulele și procedurile pentru calcularea mediei, medianei și modului.
Recunoaște diferențele în sensibilitatea la valori extreme și aplicabilitatea între medie, mediană și mod.
Interpreta histograme și identifica pozițiile mediei, medianei și modului în distribuția datelor.

Ce Este o Măsură de Tendință Centrală?

O măsură de tendință centrală este o singură valoare care reprezintă centrul sau valoarea tipică a unui set de date. Ea oferă o modalitate de a rezuma multiple puncte de date cu un singur număr reprezentativ. Măsurile de tendință centrală ne ajută să înțelegem comportamentul general sau trendul unui set de date, făcând mai ușor să tragem concluzii și să luăm decizii informate pe baza datelor.

Există trei măsuri principale de tendință centrală: media, mediana și modul. Să explorăm fiecare dintre acestea în detaliu.

1. Media: Valoarea Medie Aritmetică

Media, adesea numită valoarea medie, este cea mai comună măsură de tendință centrală. Ea este calculată prin adunarea tuturor punctelor de date dintr-un set de date și împărțirea la numărul total de puncte de date. Iată formula mediei:

\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i

Unde:

x̄: Acest simbol reprezintă media (valoarea medie) a setului de date.
n: Reprezintă numărul total de puncte de date în setul de date.
xᵢ: Reprezintă fiecare punct de date individual din setul de date, unde i este indexul variind de la 1 la n.
Σ (de la i=1 la n): Acesta este simbolul de sumare, care indică faptul că ar trebui să adunăm valorile lui xᵢ pentru toți indicii de la 1 la n. Cu alte cuvinte, adună toate punctele de date din setul de date.

Când căutăm o reprezentare grafică a mediei, ar trebui să obținem ceva asemănător cu histograma de mai jos. Aici, generăm un set de date de 100 de numere aleatorii cu o medie de 50 și o deviație standard de 10.

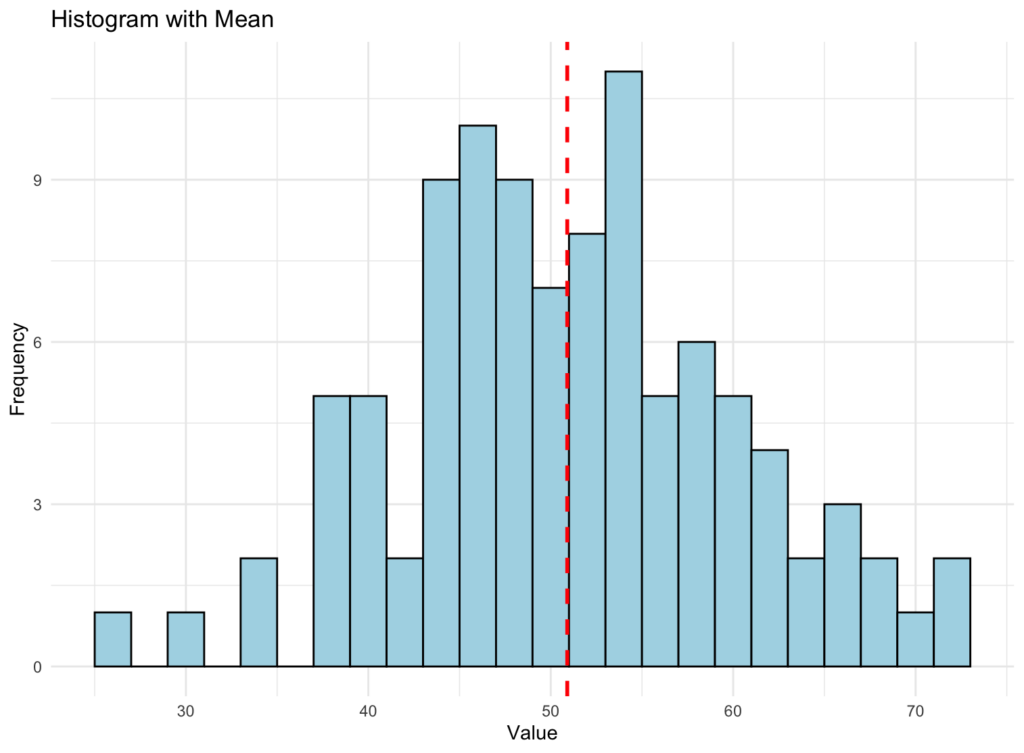
Histogramă cu Media

Histogramă arătând distribuția datelor cu linia verticală roșie reprezentând media

NOTĂ:

O histogramă este o reprezentare vizuală a setului de date. Ea împarte datele într-un anumit număr de intervale (grupuri), iar înălțimea fiecărei bare din histogramă reprezintă frecvența (de câte ori) punctele de date se încadrează în acel interval specific. Cu alte cuvinte, barele mai înalte indică mai multe puncte de date în acea gamă de valori.
Linia verticală roșie punctată din graficul de mai sus reprezintă valoarea medie a setului de date. Media este calculată prin adunarea tuturor punctelor de date și împărțirea sumei la numărul total de puncte de date. Ea oferă o idee despre tendința centrală sau "media" datelor.

Când te uiți la grafic, poți vedea cum sunt distribuite datele, iar linia verticală te ajută să identifici unde se află valoarea medie în cadrul acelei distribuții. Acest lucru îți poate oferi o idee generală despre trendul general al datelor și te ajută să înțelegi mai bine comportamentul setului de date.

Cu toate acestea, este important să ne amintim că media poate fi sensibilă la valori extreme (valori extreme), care ar putea denatura media și ar face-o mai puțin reprezentativă pentru tendința centrală a setului de date.

Învață cum să calculezi media manual, în Excel și în R în doar câțiva pași simpli.

2. Mediana: Valoarea din Mijloc

Mediana este valoarea din mijloc într-un set de date atunci când punctele de date sunt aranjate în ordine crescătoare sau descrescătoare. Deși adesea trecută cu vederea, mediana este o măsură importantă de tendință centrală, în special pentru distribuții asimetrice.

Pentru a găsi mediana, mai întâi sortează setul de date în ordine crescătoare sau descrescătoare. Dacă există un număr impar de puncte de date, mediana este valoarea din mijloc. Dacă există un număr par de puncte de date, mediana este media celor două valori din mijloc. Iată un exemplu rapid:

Set de date: $2, 4, 6, 8, 10$ . Mediana este 6 deoarece este valoarea din mijloc.
Set de date: $2, 4, 6, 8$ . Mediana este 5 deoarece media este 4 și 6, cele două valori din mijloc.

Un lucru grozav despre mediană este că este mai puțin sensibilă la valori extreme, ceea ce înseamnă că poate reprezenta mai bine centrul pentru distribuții asimetrice.

Iată cum arată reprezentarea grafică a medianei folosind aceleași criterii de set de date pe care le-am folosit mai devreme:

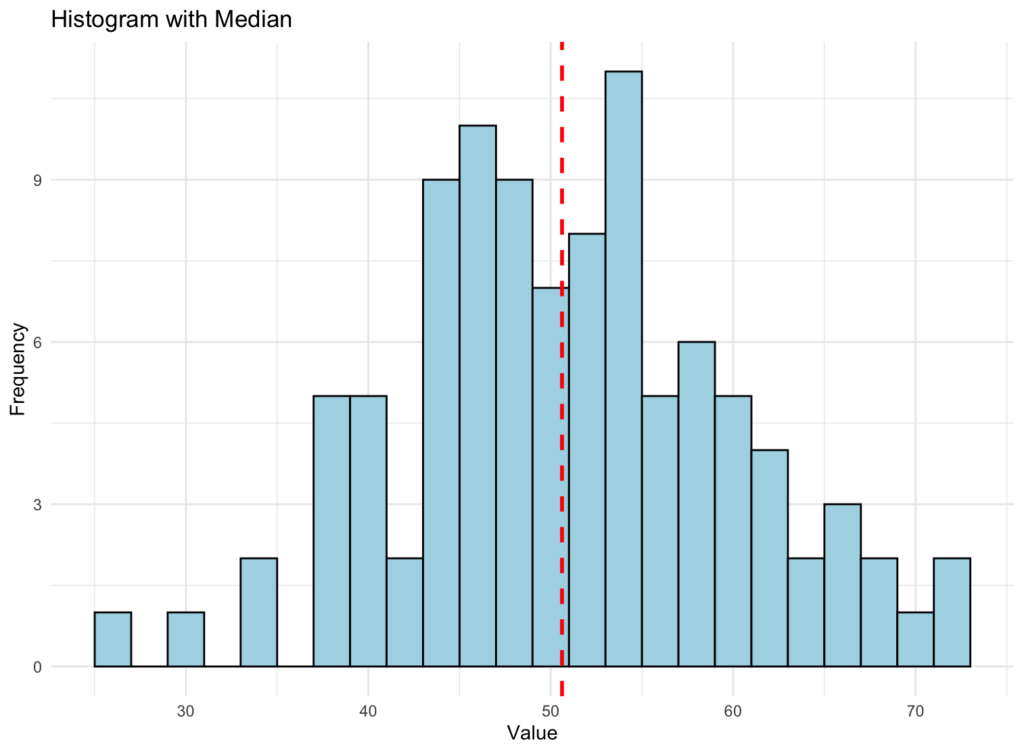
Histogramă cu Mediana

Histogramă arătând distribuția datelor cu linia verticală roșie reprezentând mediana

Histograma medianei de mai sus poate arăta asemănător cu cea anterioară pe care am generat-o pentru medie. Totuși, dacă fii atent, linia roșie punctată care reprezintă mediana este ușor deplasată. Iată explicația de ce:

Media (valoarea medie) este calculată prin adunarea tuturor punctelor de date și împărțirea sumei la numărul total de puncte de date. Ea oferă o idee despre tendința centrală sau "media" datelor. Cu toate acestea, media poate fi sensibilă la valori extreme și poate să nu reprezinte adevăratul centru al setului de date atunci când sunt prezente valori extreme.
Mediana este valoarea din mijloc a setului de date reprezentată de linia roșie punctată atunci când datele sunt sortate în ordine crescătoare sau descrescătoare. Dacă există un număr par de puncte de date, mediana este media celor două valori din mijloc. Mediana este mai puțin sensibilă la valori extreme decât media și poate reprezenta mai bine tendința centrală a setului de date atunci când sunt prezente valori extreme.

NOTĂ: În histogramele generate, liniile verticale pentru medie și mediană sunt ușor diferite deoarece reprezintă măsuri diferite de tendință centrală. Pozițiile lor pot varia în funcție de distribuția punctelor de date ale setului de date. În unele cazuri, media și mediana pot fi apropiate sau egale. În contrast, în alte cazuri, pot fi diferite din cauza prezenței valorilor extreme sau a distribuției specifice a datelor.

Învață cum să calculezi mediana manual, în Excel și în R cu ușurință.

3. Modul: Valoarea Cea Mai Frecventă

Modul este valoarea care apare cel mai frecvent într-un set de date. El reprezintă observația cea mai comună în datele tale.

Spre deosebire de medie, nu există o ecuație matematică specifică pentru calcularea modului. Modul este pur și simplu valoarea sau valorile care apar cel mai frecvent într-un set de date. Pentru a găsi modul, trebuie să numeri frecvența fiecărei valori unice din setul de date și să identifici cea (cele) cu cea mai mare frecvență.

În unele cazuri, un set de date ar putea avea:

Un mod (unimodal): O singură valoare apare mai frecvent decât orice altă valoare.
Două moduri (bimodal): Două valori diferite apar cu aceeași frecvență maximă.
Moduri multiple (multimodal): Mai mult de două valori apar cu aceeași frecvență maximă.
Fără mod: Toate valorile din setul de date apar cu aceeași frecvență.

Este important de menționat că modul poate fi folosit pentru orice tip de date, inclusiv date nominale, ordinale, de interval sau de raport, deoarece se bazează doar pe frecvența fiecărei valori unice.

Histograma pentru mod, împreună cu o linie verticală reprezentând valoarea modului, arată astfel:

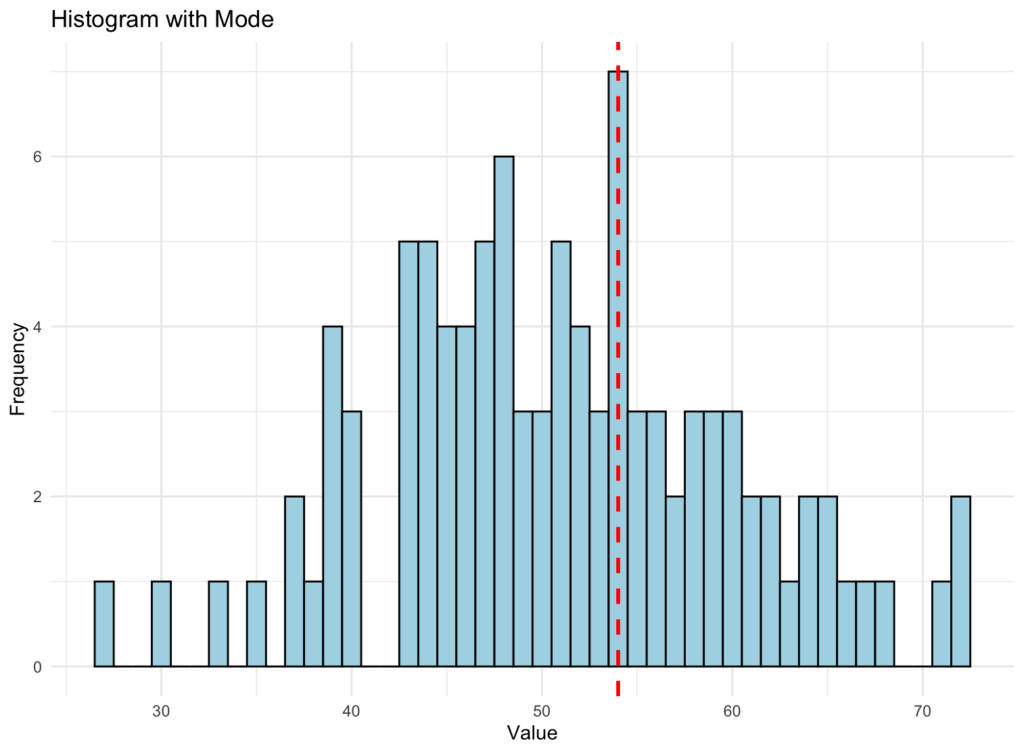
Histogramă cu Modul

Histogramă arătând distribuția datelor cu linia verticală roșie reprezentând modul

Iată o defalcare simplă a ceea ce ne spune histograma modului de mai sus:

Histograma este o reprezentare vizuală a setului de date. Ea împarte datele într-un anumit număr de intervale (grupuri), iar înălțimea fiecărei bare din histogramă reprezintă frecvența (de câte ori) punctele de date se încadrează în acel interval specific. Cu alte cuvinte, barele mai înalte indică mai multe puncte de date în acea gamă de valori.
Linia verticală roșie punctată din grafic reprezintă valoarea modului setului de date. Modul este valoarea care apare cel mai frecvent în setul de date. Este o măsură de tendință centrală care poate ajuta la identificarea celei mai comune valori sau valori ale setului de date.

Când te uiți la histograma modului, poți vedea cum sunt distribuite datele, iar linia verticală te ajută să identifici unde se află valoarea (valorile) modului în cadrul acelei distribuții.

Modul poate oferi informații despre comportamentul general al setului de date și te ajută să înțelegi cele mai comune valori. Spre deosebire de medie și mediană, modul nu este afectat de valori extreme, făcându-l o măsură potrivită de tendință centrală atunci când setul de date are o distribuție asimetrică sau conține valori extreme.

Învață cum să calculezi modul manual, în Excel și în R rapid.

De Ce Ne Pasă de Măsurile de Tendință Centrală?

Măsurile de tendință centrală sunt folosite pentru a analiza și interpreta datele în diverse domenii, cum ar fi statistică, economie, psihologie și alte științe. Ele ne ajută să:

Rezumăm seturi mari de date: În loc să analizăm fiecare punct de date în parte, putem folosi o măsură de tendință centrală pentru a obține o idee generală despre cum arată datele. Aceasta simplifică analiza noastră și face mai ușor de înțeles modelul sau trendul general al datelor.
Comparăm seturi de date diferite: Măsurile de tendință centrală ne permit să comparăm seturi de date oferind o singură valoare care reprezintă centrul fiecărui set de date. Aceasta face mai ușor să vedem care set de date are valori mai mari sau mai mici în medie.
Identificăm tendințe și modele: Uitându-ne la medie, mediană sau mod, putem identifica tendințe și modele în date. Aceasta poate fi utilă pentru a face predicții, pentru a identifica zone de îmbunătățire sau pentru a monitoriza schimbări în timp.
Luăm decizii informate: În multe domenii, factorii de decizie se bazează pe măsuri de tendință centrală pentru a-și ghida alegerile. De exemplu, un proprietar de afaceri ar putea privi la venitul mediu al diferitelor produse pentru a decide pe care să se concentreze în promovare, sau un profesor ar putea folosi scorul median al testelor pentru a determina eficiența metodelor sale de predare.

Cum Să Alegi Măsura Potrivită de Tendință Centrală

Acum că știi ce este o măsură de tendință centrală și de ce este importantă, s-ar putea să te întrebi pe care să o folosești în diferite situații. Iată câteva orientări generale pentru a te ajuta să alegi măsura potrivită pentru nevoile tale:

Folosește media când: Datele tale sunt relativ simetrice și libere de valori extreme sau extreme. Media este excelentă pentru a oferi un trend general în date și este folosită în mod obișnuit în multe domenii.
Folosește mediana când: Datele tale sunt asimetrice sau au valori extreme care ar putea afecta media. Mediana este mai puțin sensibilă la valori extreme și reprezintă mai bine centrul pentru distribuții asimetrice.
Folosește modul când: Vrei să identifici valoarea cea mai frecventă sau populară a unui set de date. Modul este deosebit de util pentru date categorice sau discrete unde alte măsuri de tendință centrală ar putea să nu fie aplicabile.

Întrebări Frecvente

Care este diferența dintre medie, mediană și mod?

Media este media aritmetică calculată prin sumarea tuturor valorilor și împărțirea la număr. Mediana este valoarea din mijloc când datele sunt ordonate de la cel mai mic la cel mai mare. Modul este valoarea care apare cel mai frecvent într-un set de date. Fiecare măsură servește scopuri diferite: media este cea mai bună pentru date distribuite normal fără valori extreme, mediana funcționează bine cu date asimetrice sau valori extreme, iar modul este ideal pentru date categorice sau pentru găsirea celei mai comune valori.

Când ar trebui să folosesc mediana în loc de medie?

Folosește mediana în loc de medie când datele tale conțin valori extreme sau sunt asimetrice (distribuite nenormal). Mediana este rezistentă la valori extreme deoarece ia în considerare doar poziția din mijloc, nu valorile efective. De exemplu, în datele despre venituri unde câțiva câștigători foarte mari pot denatura media în sus, mediana oferă o măsură mai reprezentativă a venitului tipic. Mediana este preferată și atunci când lucrezi cu date ordinale sau când valorile extreme nu reprezintă cu acuratețe tendința centrală.

Poate un set de date să aibă mai mult de un mod?

Da, un set de date poate avea mai multe moduri. Când un set de date are două moduri, se numește bimodal; cu trei moduri, este trimodal; și cu mai mult de trei, este multimodal. De exemplu, într-un set de date de scoruri la test (65, 70, 70, 80, 85, 85, 90), atât 70 cât și 85 sunt moduri deoarece apar de două ori. Un set de date fără valori repetate nu are mod. Modurile multiple pot indica diferite subgrupuri în datele tale sau mai multe vârfuri în distribuție.

Cum afectează valorile extreme măsurile de tendință centrală?

Valorile extreme afectează semnificativ media deoarece aceasta folosește toate valorile în calculul său - o singură valoare extremă poate trage media departe de centrul tipic. Mediana este rezistentă la valori extreme deoarece ia în considerare doar poziția din mijloc, nu valorile extreme efective. Modul este complet neafectat de valori extreme decât dacă valoarea extremă însăși este cea mai frecventă. De exemplu, în setul de date (10, 12, 13, 14, 100), media este 29,8 (puternic influențată de 100), dar mediana rămâne 13 (reprezentativă pentru valoarea tipică).

Ce înseamnă când media, mediana și modul sunt egale?

Când media, mediana și modul sunt egale (sau foarte apropiate), aceasta indică o distribuție simetrică, normală, fără asimetrie. Aceasta este curba clasică în formă de clopot unde datele sunt distribuite uniform în jurul centrului. În astfel de distribuții, toate cele trei măsuri indică aceeași valoare centrală, făcând oricare dintre ele o măsură fiabilă a tendinței centrale. Acest lucru este obișnuit în fenomene care apar natural, precum înălțimea umană, scorurile la teste în populații mari sau erorile de măsurare.

Cum calculez mediana cu un număr par de valori?

Când ai un număr par de valori, mediana este media celor două valori din mijloc. Mai întâi, aranjează datele tale în ordine de la cel mai mic la cel mai mare. Apoi identifică cele două numere din mijloc și calculează media lor. De exemplu, în setul de date (3, 5, 7, 9), cele două valori din mijloc sunt 5 și 7. Mediana este (5 + 7) / 2 = 6. Cu un număr impar de valori, mediana este pur și simplu valoarea din mijloc după ordonarea datelor.

Care măsură de tendință centrală este cea mai bună pentru date categorice?

Modul este singura măsură potrivită de tendință centrală pentru date categorice (nominale) deoarece nu poți calcula o medie sau o valoare din mijloc semnificativă pentru categorii precum culori, nume sau tipuri. De exemplu, dacă faci un sondaj despre culorile preferate și obții (roșu, albastru, albastru, verde, albastru, roșu, albastru), modul este albastru (apare de 4 ori). Nu poți calcula o medie sau mediană pentru categorii de culori deoarece nu au valori numerice sau o ordine naturală. Pentru date ordinale (categorii ordonate precum clasamentele), poți folosi modul sau mediana, dar nu media.

Ce este o medie ponderată și când este folosită?

O medie ponderată atribuie niveluri diferite de importanță (ponderi) diferitelor valori din setul tău de date, mai degrabă decât să trateze toate valorile în mod egal. Este calculată prin înmulțirea fiecărei valori cu ponderea sa, sumând aceste produse și împărțind la suma ponderilor. Formula este: Medie Ponderată = Σ(valoare × pondere) / Σ(ponderi). Folosește medii ponderate când unele observații sunt mai importante decât altele, cum ar fi calcularea mediilor generale (unde diferite cursuri au ore de credit diferite), indicii financiari (unde companiile au capitalizări de piață diferite) sau datele de sondaj (unde răspunsurile sunt ponderate pentru a se potrivi cu demografia populației).

Concluzie

Măsurile de tendință centrală (media, mediana și modul) oferă instrumente esențiale pentru rezumarea și înțelegerea distribuțiilor de date. Fiecare măsură oferă avantaje unice. Media furnizează o valoare medie generală, mediana rezistă influenței valorilor extreme, iar modul identifică cea mai comună valoare în setul tău de date.

Selectând măsura potrivită de tendință centrală pentru caracteristicile specifice ale datelor tale și întrebările de cercetare, poți trage concluzii mai precise și lua decizii mai bine informate din analizele tale statistice.