Corelația Pearson în Excel: Ghid Pas cu Pas (Funcția CORREL)

Învață cum să calculezi coeficientul de corelație Pearson în Excel folosind funcția CORREL și Data Analysis Toolpak. Acest ghid pas cu pas îți arată cum să măsori corelația dintre două variabile, să interpretezi rezultatele și să verifici presupozițiile.

Coeficientul de corelație Pearson măsoară puterea și direcția relației liniare dintre două variabile continue. Funcția CORREL încorporată în Excel facilitează calcularea rapidă a coeficienților de corelație, fie că analizezi cheltuieli de publicitate vs venituri, scoruri de test vs ore de studiu sau orice alte două variabile corelate.

Descarcă setul de date pentru practică din bara laterală (parolă: uedufy) și urmărește exemplele.

Ce Este Coeficientul de Corelație Pearson?

Să presupunem că deții un magazin de îmbrăcăminte și vrei să vezi dacă există o relație între cât cheltuiești pe publicitate și câți bani faci. Aici intervine util coeficientul de corelație Pearson!

Pe de altă parte, dacă coeficientul este aproape de -1, înseamnă că pe măsură ce cheltuiești mai mult pe publicitate, venitul tău este probabil să scadă. Iar dacă coeficientul este aproape de 0, nu există o relație reală între publicitate și venituri.

Ai analizat datele tale și coeficientul de corelație Pearson a fost 0.8. Aceasta înseamnă că există o relație pozitivă puternică între Publicitate și Venituri: cu cât cheltuiești mai mult pe publicitate, cu atât faci mai mulți bani! Dar nu te entuziasma prea mult încă. Și alți factori pot afecta venitul. Cunoașterea coeficientului de corelație Pearson este doar o piesă din puzzle, dar o metrică importantă de luat în considerare.

Coeficientul de corelație Pearson măsoară puterea relației dintre două lucruri, în acest caz, publicitate și venituri. Dacă coeficientul este aproape de 1, înseamnă că pe măsură ce cheltuiești mai mult pe publicitate, vei vedea probabil o creștere a veniturilor.

$r=\frac{\sum\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum\left(x_i-\bar{x}\right)^2 \sum\left(y_i-\bar{y}\right)^2}}$

Unde:

r este coeficientul de corelație
xi reprezintă valorile variabilei x într-un eșantion
x̄ este media valorilor variabilei x
yi reprezintă valorile variabilei y într-un eșantion
ȳ este media valorilor variabilei y

Presupozițiile Corelației Pearson

Înainte de a calcula coeficientul de corelație Pearson în Excel, verifică dacă datele tale îndeplinesc aceste presupozițiiț:

1. Variabile Continue

Ambele variabile ar trebui să fie măsurate pe o scală continuă (nivel interval sau rație). Corelația Pearson NU este adecvată pentru date categoriale sau ordinale.

Exemple de variabile continue: înălțime, greutate, temperatură, scoruri de test, venituri, timp

2. Liniaritate

Relația dintre cele două variabile ar trebui să fie liniară. Aceasta înseamnă că pe măsură ce o variabilă crește, cealaltă variabilă crește (sau scade) cu o rată constantă.

Cum să verifici în Excel: Creează un grafic de dispersie al datelor tale. Dacă punctele formează aproximativ un model de linie dreaptă (nu o curbă), presupunerea de liniaritate este îndeplinită.

3. Independența Observațiilor

Fiecare observație ar trebui să fie independentă, ceea ce înseamnă că valoarea unei observații nu ar trebui să influențeze sau să fie legată de valoarea altei observații.

Exemplu: Măsurarea aceleiași persoane de mai multe ori încalcă independența. Fiecare punct de date ar trebui să provină de la un subiect diferit sau o ocazie de măsurare diferită.

4. Normalitatea Bivariată

Pentru testarea semnificației precise, ambele variabile ar trebui să urmeze o distribuție normală bivariată. Cu toate acestea, corelația Pearson este destul de robustă la încălcările normalității pentru dimensiuni mai mari ale eșantionului (n > 30).

Cum să verifici în Excel: Creează histograme pentru fiecare variabilă pentru a evalua vizual normalitatea. Pentru eșantioane mai mici de 30, ia în considerare utilizarea testelor de normalitate.

Ce se întâmplă dacă presupozițiile sunt încălcate?

Dacă datele tale încalcă aceste presupozițiii (în special liniaritatea sau normalitatea), ia în considerare utilizarea coeficientului de corelație de rang Spearman, care este o alternativă neparametrică ce nu necesită aceste presupozițiii stricte.

Metoda 1: Calculează Coeficientul de Corelație în Excel folosind Funcția CORREL

Să revenim la exemplul nostru de magazin de îmbrăcăminte și să învățăm cum să calculăm coeficientul de corelație Pearson în Excel pentru a afla dacă există o relație între cât cheltuim pe publicitate și câți bani facem.

1. Pregătește datele tale: Organizează datele în două coloane, cu o coloană reprezentând fiecare dintre cele două variabile pe care dorești să le analizezi. În setul meu de date, cele două variabile pe care vrem să verificăm dacă sunt corelate sunt Publicitate și Venituri.

Set de date Excel pentru coeficientul de corelație Pearson arătând două coloane pentru variabilele Publicitate și Venituri

Exemplu de două variabile pentru calculul coeficientului de corelație în Excel.

2. Selectează o celulă: Alege o celulă în foaia de calcul unde ai dori să afișezi rezultatul coeficientului de corelație Pearson.

Foaie de calcul Excel cu celulă selectată pentru afișarea rezultatului coeficientului de corelație Pearson

Selectează o celulă în foaia de calcul pentru rezultatul corelației.

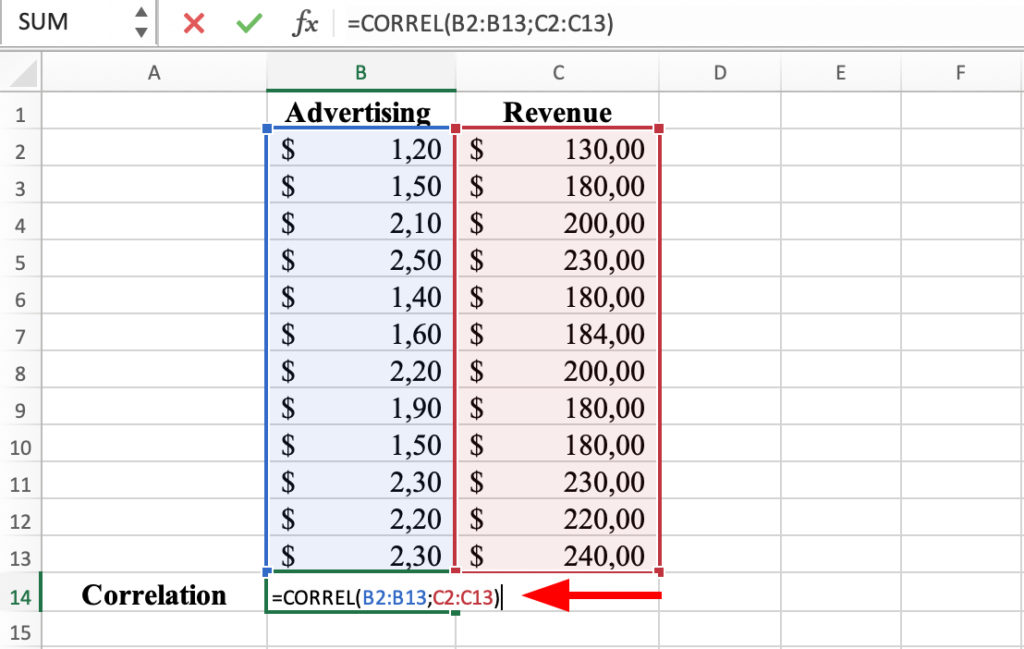
3. Introdu funcția de corelație: Tastează "=CORREL(" urmat de intervalul primei coloane de date, o virgulă și intervalul celei de-a doua coloane de date și închide parantezele. De exemplu, dacă datele tale sunt în coloanele B și C (ca în captura de mai jos), funcția de corelație ar arăta astfel: =CORREL(B2:B13, C2:C13).

Excel arătând sintaxa funcției CORREL pentru calcularea coeficientului de corelație Pearson

Funcția CORREL în Excel.

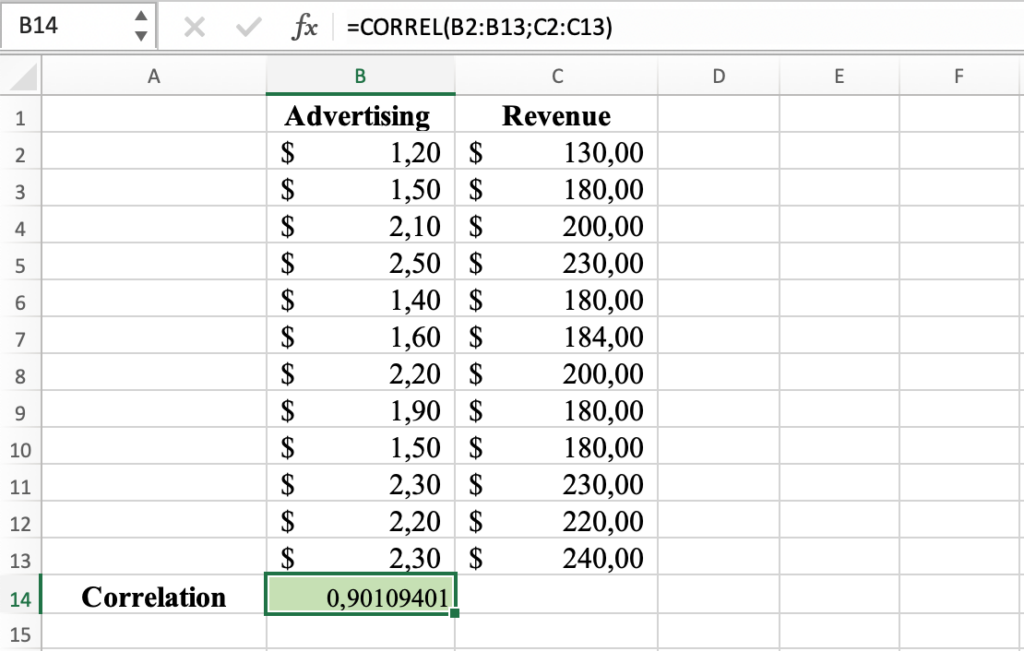
4. Calculează rezultatul: Apasă tasta ENTER pentru a calcula coeficientul de corelație Pearson. Rezultatul va fi afișat în celula selectată. Coeficientul de corelație dintre Publicitate și Venituri în setul nostru de date este 0.9.

Excel afișând rezultatul coeficientului de corelație Pearson de 0.9

Rezultatul coeficientului de corelație Pearson pentru variabilele selectate.

Metoda 2: Calculează Coeficientul de Corelație folosind Instrumentul de Analiză în Excel

Iată o altă modalitate de a calcula corelația dintre două variabile în Excel folosind Data Analysis Toolpak.

1. Pregătește datele tale: Asigură-te că datele tale sunt organizate în două coloane, fiecare coloană reprezentând o variabilă (la fel cum am făcut înainte).

2. Instalează instrumentul Data Analysis în Excel: dacă nu vezi pictograma Data Analysis în fila ta Data din Excel, ar trebui să instalezi mai întâi Data Analysis Toolpak.

Panglica Excel arătând locația butonului Data Analysis în fila Data

Locația Data Analysis în Excel.

3. Lansează instrumentul Data Analysis: Din fila Data, fă clic pe Data Analysis și selectează Correlation.

Caseta de dialog Excel Data Analysis cu opțiunea Correlation selectată

Data Analysis - Correlation.

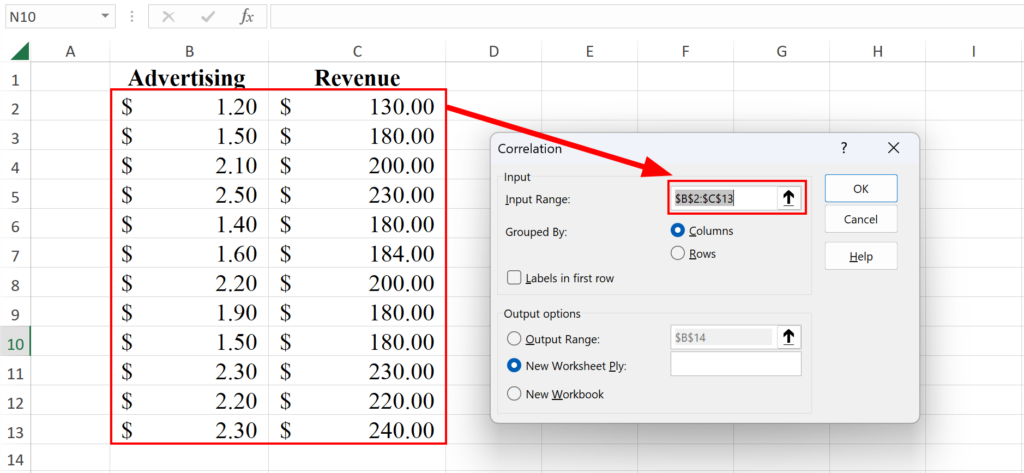
4. Selectează datele: În caseta de dialog Data Analysis, selectează intervalul de intrare, care este intervalul celor două coloane de date. Dacă ai inclus etichetele de coloană în selecția ta (Publicitate și Venituri), bifează caseta Labels in First Row.

NOTĂ: În secțiunea "Output Options", poți alege și unde dorești să fie afișat rezultatul, fie într-o foaie de calcul nouă, fie într-un interval de celule. Să lăsăm setarea implicită deocamdată.

Caseta de dialog Excel Correlation arătând selecția intervalului de intrare pentru datele Publicitate și Venituri

Selectează intervalul de valori pentru corelație.

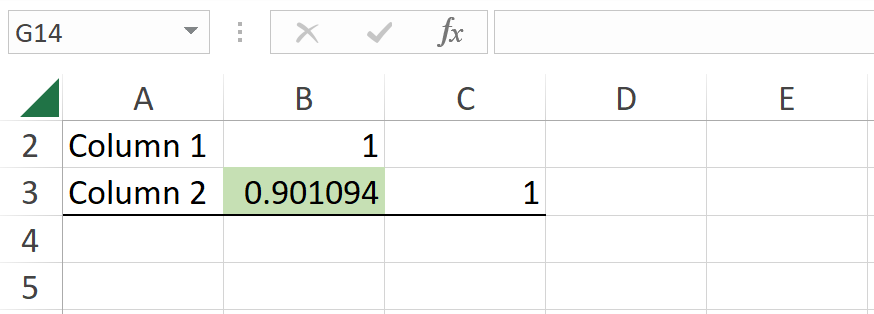
5. Rulează analiza: Fă clic pe OK pentru a calcula. Rezultatul coeficientului de corelație Pearson va fi afișat în locația de ieșire pe care ai selectat-o. Așa cum era de așteptat, pentru același set de date, coeficientul este același: 0.9.

Ieșire Excel arătând rezultatul coeficientului de corelație Pearson de 0.9 folosind Data Analysis Toolpak

Rezultatul coeficientului de corelație Pearson în Excel.

Cum Să Interpretezi Rezultatele Corelației Pearson

Coeficientul de corelație Pearson (r) va fi întotdeauna o valoare între -1 și 1. Iată cum să interpretezi rezultatele în Excel:

Înțelegerea Valorilor Corelației

Valoarea Coeficientului:

r = 1: Corelație pozitivă perfectă (pe măsură ce o variabilă crește, cealaltă crește proporțional)
r = -1: Corelație negativă perfectă (pe măsură ce o variabilă crește, cealaltă scade proporțional)
r = 0: Fără corelație liniară (fără relație liniară între variabile)

Direcție:

Corelație pozitivă (0 până la 1): Ambele variabile se mișcă în aceeași direcție
Corelație negativă (0 până la -1): Variabilele se mișcă în direcții opuse

Interpretarea Puterii Corelației

Folosește aceste orientări pentru a interpreta puterea coeficientului tău de corelație Pearson:

Valoarea Corelației	Putere	Interpretare
0.9 până la 1.0 (sau -0.9 până la -1.0)	Foarte puternică	Variabilele sunt foarte corelate
0.7 până la 0.9 (sau -0.7 până la -0.9)	Puternică	Există o relație puternică
0.4 până la 0.7 (sau -0.4 până la -0.7)	Moderată	Relație moderată
0.1 până la 0.4 (sau -0.1 până la -0.4)	Slabă	Relație slabă
0 până la 0.1 (sau 0 până la -0.1)	Niciunun	Fără corelație semnificativă

Exemplu de Interpretare

În exemplul nostru, coeficientul de corelație de r = 0.9 indică o corelație pozitivă foarte puternică între variabilele Publicitate și Venituri.

Ce înseamnă acest lucru:

Pe măsură ce cheltuielile de publicitate cresc cu 1 unitate, veniturile tind să crească cu o rată foarte consecventă
81% din variația veniturilor poate fi explicată prin cheltuielile de publicitate (calculat ca r² = 0.9² = 0.81)
Aceasta este o relație foarte puternică, dar nu dovedește cauzalitatea

Important: Corelație vs Cauzalitate

Memento critic: Un coeficient de corelație Pearson ridicat NU înseamnă că o variabilă cauzează cealaltă. Arată doar că tind să se schimbe împreună.

De ce contează acest lucru:

Corelația arată asocierea, nu cauzalitatea
O a treia variabilă ar putea influența ambele variabile
Relația ar putea fi coincidentală
Ar putea exista cauzalitate inversă (B cauzează A, nu A cauzează B)

Pentru a stabili cauzalitatea, ai nevoie de designuri de cercetare experimentală sau metode statistice suplimentare precum analiza de regresie.

Pearson vs Spearman: Care Să Folosești?

Când analizezi corelația în Excel, te-ai putea întreba dacă să folosești corelația Pearson sau Spearman. Iată cum să alegi metoda potrivită:

Coeficientul de Corelație Pearson

Folosește Pearson când:

Ambele variabile sunt continue (scală interval sau rație)
Relația dintre variabile este liniară
Datele sunt aproximativ distribuite normal
Nu sunt prezente valori aberante semnificative

Avantaje:

Test statistic mai puternic (mai bun la detectarea corelațiilor adevărate)
Larg recunoscut și raportat frecvent în cercetare
Ușor de calculat în Excel folosind funcția CORREL

Dezavantaje:

Sensibil la valori aberante
Necesită presupozițiii (liniaritate, normalitate)
Detectează doar relații liniare

Coeficientul de Corelație Spearman

Folosește Spearman când:

Variabilele sunt ordinale (date clasificate)
Relația este monotonă dar nu neapărat liniară
Datele conțin valori aberante
Datele nu sunt distribuite normal

Avantaje:

Neparametric (nu necesită presupozițiii de distribuție)
Robust la valori aberante
Funcționează cu date clasificate/ordinale
Detectează relații monotone (nu doar liniare)

Dezavantaje:

Mai puțin puternic decât Pearson când presupozițiile sunt îndeplinite
Mai complex de calculat în Excel (necesită clasificarea datelor mai întâi)
Poate rata unele nuanțe ale relației

Ghid Rapid de Decizie

Alege corelația Pearson dacă:

Datele tale sunt continue și distribuite normal
Graficul de dispersie arată un model aproximativ liniar
Nu ai valori aberante extreme

Alege corelația Spearman dacă:

Datele tale sunt ordinale/clasificate
Graficul de dispersie arată un model curbat sau neliniar
Ai valori aberante semnificative
Datele tale încalcă presupozițiile de normalitate

Exemplu: Dacă corelezi scoruri de test (continue, distribuite normal) cu ore de studiu (continue), folosește Pearson. Dacă corelezi clasificări de satisfacție a clienților (ordinale: 1-5 stele) cu evaluări de calitate a produsului, folosește Spearman.

Pentru majoritatea utilizatorilor Excel care lucrează cu date continue, distribuite normal, corelația Pearson este alegerea adecvată.

Întrebări Frecvente

Ce este coeficientul de corelație Pearson?

Coeficientul de corelație Pearson (numit și Pearson's r) este o măsură statistică care calculează puterea și direcția relației liniare dintre două variabile continue. Variază de la -1 la +1, unde -1 indică o corelație negativă perfectă, +1 indică o corelație pozitivă perfectă și 0 indică lipsa corelației liniare.

Cum interpretez rezultatele corelației Pearson în Excel?

Interpretează valorile corelației Pearson după cum urmează: 0.7 până la 1.0 (sau -0.7 până la -1.0) indică o corelație puternică, 0.4 până la 0.7 (sau -0.4 până la -0.7) indică o corelație moderată, 0.1 până la 0.4 (sau -0.1 până la -0.4) indică o corelație slabă și 0 până la 0.1 (sau 0 până la -0.1) indică lipsa corelației. Valorile pozitive înseamnă că variabilele cresc împreună, în timp ce valorile negative înseamnă că una crește pe măsură ce cealaltă scade.

Care este diferența dintre corelația Pearson și Spearman?

Corelația Pearson măsoară relațiile liniare dintre variabilele continue și presupune normalitatea bivariată. Corelația Spearman este un test neparametric care măsoară relațiile monotone (nu neapărat liniare) și funcționează cu date clasificate sau ordinale. Folosește Pearson când datele tale sunt distribuite normal și relația este liniară; folosește Spearman când datele nu sunt distribuite normal sau conțin valori aberante.

Poate corelația Pearson să dovedească cauzalitatea?

Nu, corelația Pearson NU dovedește cauzalitatea. Măsoară doar puterea și direcția asocierii între două variabile. O corelație ridicată înseamnă că variabilele tind să se schimbe împreună, dar nu îți spune care variabilă cauzează schimbări în cealaltă sau dacă o a treia variabilă influențează ambele. Pentru a stabili cauzalitatea, ai nevoie de designuri de cercetare experimentală sau metode statistice suplimentare precum analiza de regresie.

Ce dimensiune a eșantionului am nevoie pentru corelația Pearson în Excel?

Deși corelația Pearson poate fi calculată tehnic cu eșantioane mici, ai nevoie de cel puțin n=30 pentru rezultate fiabile și testarea semnificației. Eșantioanele mai mici (n<30) sunt mai sensibile la valori aberante și încălcări ale presupozițiilor de normalitate. Pentru detectarea corelațiilor mici (r=0.1-0.3), ar putea fi nevoie de 100+ observații pentru putere statistică adecvată.

Cum calculez valoarea p pentru corelația Pearson în Excel?

Funcția CORREL din Excel calculează doar coeficientul de corelație, nu valoarea p. Pentru a obține valoarea p, trebuie să folosești instrumentul Correlation din Data Analysis Toolpak (care de asemenea nu oferă direct valorile p) sau să o calculezi manual folosind funcția T.DIST cu formula: t = r × sqrt((n-2)/(1-r²)), unde r este coeficientul de corelație și n este dimensiunea eșantionului.

Ce înseamnă o corelație de 0.9?

O corelație de 0.9 indică o relație liniară pozitivă foarte puternică între două variabile. Aceasta înseamnă că pe măsură ce o variabilă crește, cealaltă variabilă tinde să crească cu o rată foarte consecventă. Cu toate acestea, amintește-ți că chiar și o corelație de 0.9 înseamnă că doar 81% (0.9²) din variația unei variabile poate fi explicată prin cealaltă variabilă - există încă 19% variație neexplicată.

Concluzie

Coeficientul de corelație Pearson este un instrument util pentru înțelegerea relației dintre două variabile și este ușor de calculat în Excel folosind fie Data Analysis Toolpak, fie funcția CORREL.