Homoscedasticity เป็นข้อสมมติฐานพื้นฐานที่สำคัญใน Linear Regression และการสร้างแบบจำลองทางสถิติ การเข้าใจความหมายของ Homoscedasticity ซึ่งหมายถึง ความคงที่ของ Variance ของ Residuals เป็นสิ่งจำเป็นสำหรับการสร้างผลลัพธ์ทางสถิติที่ถูกต้องและเชื่อถือได้
คู่มือนี้จะอธิบายข้อสมมติฐาน Homoscedasticity ในสถิติ วิธีการตรวจจับการละเมิดข้อสมมติฐาน (Heteroscedasticity) และแนวทางแก้ไขปัญหาที่ใช้ได้จริง คุณจะได้เรียนรู้ความแตกต่างสำคัญระหว่าง Homoscedasticity vs Heteroscedasticity และเหตุใดการละเมิดข้อสมมติฐานนี้จึงนำไปสู่ผลการทดสอบสมมติฐานและ Confidence Intervals ที่ไม่น่าเชื่อถือใน Regression Analysis
Homoscedasticity คืออะไร?
Homoscedasticity (อ่านว่า "โฮโม-สเคด-แอสติซิตี้") อธิบายถึง ความคงที่ของ Variance ของ Residuals หรือ Errors ในทุกระดับของตัวแปรอิสระในชุดข้อมูล
คำนิยาม: ในชุดข้อมูลที่เป็น Homoscedastic การกระจายของจุดข้อมูลจะคงที่ไม่ว่าค่าของตัวแปรพยากรณ์จะเป็นเท่าใด Variance จะไม่เปลี่ยนแปลงเมื่อตัวแปรอิสระเปลี่ยนแปลง
ตัวอย่าง: ในการทดสอบย่อยในห้องเรียน หากความผันแปรของคะแนนมีความคล้ายคลึงกันในทุกระดับความสามารถ นั่นคือ Homoscedasticity นักเรียนทุกคนแสดงการกระจายของคะแนนที่คล้ายคลึงกันไม่ว่าทักษะของพวกเขาจะเป็นอย่างไร
Heteroscedasticity (ตรงกันข้าม) เกิดขึ้นเมื่อ Variance เปลี่ยนแปลงไปตามระดับของตัวแปรอิสระ ในตัวอย่างการทดสอบ Variance อาจสูงกว่าสำหรับนักเรียนขั้นสูงและต่ำกว่าสำหรับผู้เริ่มต้น - การกระจายไม่คงที่
Homoscedasticity และ Linear Regression
Homoscedasticity เป็นข้อสมมติฐานที่สำคัญใน Linear Regression ด้วยเหตุผลหลายประการ:
-
ประสิทธิภาพของ Estimators: เมื่อ Homoscedasticity เป็นจริง Ordinary Least Squares (OLS) ให้ค่าประมาณเชิงเส้นที่ไม่เอนเอียงที่ดีที่สุด (BLUE - Best Linear Unbiased Estimator) ที่มี Variance ต่ำที่สุด Heteroscedasticity ทำให้ OLS Estimators ไม่มีประสิทธิภาพ
-
ความถูกต้องของการทดสอบสมมติฐาน: การทดสอบสมมติฐาน (t-tests, F-tests) สมมติว่ามี Homoscedasticity การละเมิดนำไปสู่ Test Statistics และ p-values ที่ไม่น่าเชื่อถือ ทำให้สรุปผลเกี่ยวกับนัยสำคัญของ Coefficients ได้ไม่ถูกต้อง
-
Confidence Intervals: ข้อมูล Homoscedastic สร้าง Confidence Intervals ที่แม่นยำ Heteroscedasticity สร้าง Intervals ที่กว้างหรือแคบเกินไป นำไปสู่การอนุมานที่ไม่ถูกต้อง
-
ความแม่นยำในการพยากรณ์: เมื่อ Variance คงที่ การพยากรณ์ของแบบจำลองมีความน่าเชื่อถือสม่ำเสมอในทุกระดับของ Predictors Heteroscedasticity ทำลายความแม่นยำในการพยากรณ์เนื่องจากความผันแปรของ Residuals เปลี่ยนแปลง
การตรวจจับ Homoscedasticity (และ Heteroscedasticity)
ตอนนี้เราได้ครอบคลุมว่า Homoscedasticity คือะไรและทำไมมันจึงสำคัญแล้ว มาพูดถึงวิธีการตรวจจับในข้อมูลของคุณ มีหลายวิธีในการตรวจสอบ Homoscedasticity รวมถึงวิธีการทางกราฟิกและการทดสอบทางสถิติ
วิธีการทางกราฟิก (Graphical Methods)
สร้าง Scatterplot ของ Residuals เทียบกับ Fitted Values ในข้อมูล Homoscedastic จุดควรกระจายอย่างสม่ำเสมอโดยไม่มีรูปแบบหรือกลุ่มที่เห็นได้ชัด
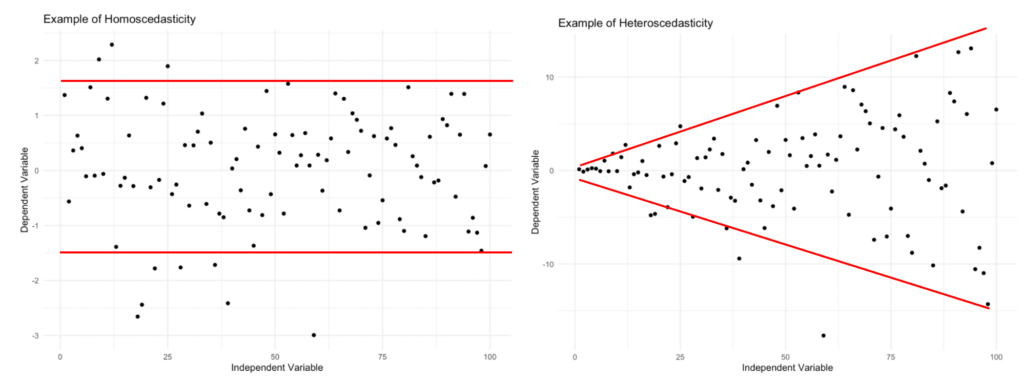 Homoscedasticity vs. Heteroscedasticity: Variance คงที่ (ซ้าย) เทียบกับ Variance ที่เปลี่ยนแปลง (ขวา)
Homoscedasticity vs. Heteroscedasticity: Variance คงที่ (ซ้าย) เทียบกับ Variance ที่เปลี่ยนแปลง (ขวา)
การทดสอบทางสถิติ (Statistical Tests)
หากคุณต้องการวิธีการที่เป็นทางการมากขึ้น มีการทดสอบทางสถิติหลายแบบที่ใช้ตรวจสอบ Homoscedasticity ได้ การทดสอบที่นิยมใช้ ได้แก่:
-
Bartlett's Test: ตรวจสอบ Variances ที่เท่ากันในหลายกลุ่ม ผลลัพธ์ที่มีนัยสำคัญบ่งชี้ Heteroscedasticity
-
Levene's Test: คล้ายกับ Bartlett's Test, Levene's Test ตรวจสอบ Variances ที่เท่ากันในกลุ่มต่างๆ ไวต่อการไม่เป็น Normal น้อยกว่า ทำให้มีความแข็งแกร่งมากกว่า
-
Breusch-Pagan Test: ใช้ใน Regression Analysis ทดสอบว่า Squared Residuals สัมพันธ์กับตัวแปรอิสระหรือไม่ ผลลัพธ์ที่มีนัยสำคัญบ่งชี้ Heteroscedasticity
-
White Test: การทดสอบที่กว้างกว่าสำหรับ Heteroscedasticity ใน Regression ตรวจสอบว่า Squared Residuals สัมพันธ์กับการผสมเชิงเส้นหรือกำลังสองของตัวแปรอิสระหรือไม่
โปรดทราบว่าไม่มีการทดสอบใดที่สมบูรณ์แบบ และแต่ละแบบมีข้อจำกัด ในบางกรณี อาจเป็นประโยชน์ที่จะใช้การทดสอบหลายแบบหรือรวมกับวิธีการทางกราฟิกเพื่อให้ได้การประเมิน Homoscedasticity ที่แม่นยำยิ่งขึ้น
การแก้ไขปัญหา Heteroscedasticity
หากคุณพบว่าข้อมูลของคุณเป็น Heteroscedastic มีกลยุทธ์หลายวิธีในการจัดการกับปัญหานี้:
-
Transformation (การแปลงค่า): แปลงตัวแปร (Logarithm, Square Root, Reciprocal) เพื่อทำให้ Variance คงที่ โปรดทราบว่าการแปลงค่าจะเปลี่ยนการแปลผลลัพธ์
-
Weighted Regression: ให้น้ำหนักมากขึ้นกับการสังเกตที่มี Variances เล็กกว่า และน้ำหนักน้อยลงกับ Variances ที่ใหญ่กว่า ทำให้ Variance คงที่ในช่วงของ Predictors
-
Robust Regression: ใช้วิธีการที่ไวต่อ Outliers และการละเมิดข้อสมมติฐานน้อยกว่า ให้ค่าประมาณที่แม่นยำยิ่งขึ้นกับข้อมูล Heteroscedastic
-
Bootstrapping: เทคนิคการสุ่มตัวอย่างซ้ำที่ให้ค่าประมาณ Parameters ของประชากรที่แม่นยำแม้จะมี Heteroscedasticity
การอ่านค่า / การแปลผล
เมื่อตรวจสอบ Homoscedasticity ในงานวิจัยของคุณ การแปลผลควรพิจารณาดังนี้:
การแปลผลแบบกราฟิก:
- หาก Residual Plot แสดงจุดกระจายแบบสุ่มรอบเส้น 0 โดยไม่มีรูปแบบ = Homoscedastic (ผ่านข้อสมมติฐาน)
- หากเห็นรูปแบบกรวย (Funnel/Cone Shape) = Heteroscedastic (ไม่ผ่านข้อสมมติฐาน)
การแปลผลการทดสอบทางสถิติ:
- p-value > 0.05 = ไม่ปฏิเสธ Null Hypothesis = ข้อมูลเป็น Homoscedastic
- p-value ≤ 0.05 = ปฏิเสธ Null Hypothesis = ข้อมูลเป็น Heteroscedastic
ข้อแนะนำ:
- หากพบ Heteroscedasticity ไม่รุนแรง (p-value ใกล้ 0.05) อาจดำเนินการวิเคราะห์ต่อไปได้โดยระมัดระวังในการแปลผล
- หากพบ Heteroscedasticity รุนแรง (p-value < 0.01) ควรแก้ไขก่อนทำการวิเคราะห์
- แนะนำให้ใช้ทั้งวิธีกราฟิกและการทดสอบทางสถิติร่วมกันเพื่อความมั่นใจในการตัดสินใจ
Homoscedasticity vs. Heteroscedasticity: ความแตกต่างสำคัญ
| ด้าน | Homoscedasticity | Heteroscedasticity |
|---|---|---|
| Variance | คงที่ในทุกระดับของ Predictor | เปลี่ยนแปลงตามระดับของ Predictor |
| รูปแบบภาพ | จุดกระจายแบบสุ่ม ไม่มีรูปแบบ | รูปทรงกรวยหรือพัด |
| ประสิทธิภาพ OLS | BLUE (Best Linear Unbiased Estimator) | ไม่มีประสิทธิภาพ, Standard Errors ใหญ่กว่า |
| การทดสอบสมมติฐาน | p-values และ Confidence Intervals ที่ถูกต้อง | p-values ไม่น่าเชื่อถือ, การอนุมานผิดพลาด |
| ผลกระทบ | ผลลัพธ์เชื่อถือได้ | Standard Errors เอนเอียง, การทดสอบเข้าใจผิด |
คำถามที่พบบ่อย (FAQs)
สรุป
Homoscedasticity - ความคงที่ของ Variance ของ Residuals - เป็นข้อสมมติฐานที่สำคัญใน Linear Regression และการทดสอบทางสถิติหลายแบบ การละเมิดข้อสมมติฐานนี้นำไปสู่ Standard Errors ที่ไม่น่าเชื่อถือ การทดสอบสมมติฐานที่ไม่ถูกต้อง และ Confidence Intervals ที่ผิดพลาด
ประเด็นสำคัญ:
- Homoscedasticity คืออะไร: Variance คงที่ในทุกระดับของ Predictor
- วิธีการตรวจสอบ: กราฟภาพ (Residual Scatter) และการทดสอบทางสถิติ (Breusch-Pagan, Levene's, White)
- แนวทางแก้ไข: การแปลงข้อมูล, Weighted Regression, วิธี Robust, Bootstrapping
- ผลกระทบ: ทำให้มั่นใจได้ว่าผลลัพธ์ทางสถิติถูกต้องและเชื่อถือได้
สำหรับผู้ที่สนใจ การวิเคราะห์ Linear Regression ใน SPSS หรือ การวิเคราะห์ Multiple Regression ใน SPSS การตรวจสอบข้อสมมติฐาน Homoscedasticity เป็นขั้นตอนที่จำเป็นก่อนการแปลผลลัพธ์