How to Calculate Standard Error in Excel, SPSS & R: Formula & Examples

In this comprehensive tutorial, you'll learn how to calculate standard error in Excel, SPSS, and R with step-by-step examples and downloadable datasets. Whether you need to find standard error in Excel using formulas, calculate standard error in SPSS with descriptive statistics, or compute it in R, this guide covers everything you need.

We'll cover the standard error formula, its interpretation, and practical calculations across all three platforms with real examples.

Note: The terms "standard error" and "estimated standard error of the mean" are used interchangeably in statistics and refer to the same concept.

What is the Standard Error of the Mean

In an ideal scenario, researchers would have access to entire populations for their studies. However, this is rarely feasible in practice.

In most cases, we collect data by sampling the population we investigate. If we take multiple samples of the same population we will observe that they are slightly different.

For instance, the mean of each sample will be different from another as each sample likely contains different members of the same population.

So how do we know if sample data represent a whole population?

This is where the standard error of the mean (or simply, standard error) becomes essential. Here are the common notations used by various authors in the literature:

$SE \qquad SEM \qquad SE(\bar{x}) \qquad SE_{\bar{x}} \qquad s_{\bar{x}}$

The standard error is used to determine how close the mean of a sample taken from a population is compared to the average value of the true population.

A lower standard error value shows that the sample means have a close distribution around the population mean therefore more representative of the true population.

In contrast, a higher standard error value likely shows that the sample is an inaccurate representation of the true population.

The best way to lower a high standard error value is by increasing the sample size. We will do a comparison later in this lesson.

It is also important to use random sampling when collecting the data to avoid sampling bias.

Finally, you should really understand the **difference between the standard error of the mean and standard deviation**in statistics. The two are often a source of great confusion among students.

How To Find Standard Error of the Mean

The below formula is the equation for the standard error of the mean using the population standard deviation:

$SE = \frac{\sigma}{\sqrt{n}}$

Where:

$SE$ = Standard error of the mean
$\sigma$ = Population standard deviation
$n$ = Sample size
$\sqrt{n}$ = Square root of the sample size

The caveat here is that we need to know the actual population standard deviation to be able to calculate the standard error using the above formula.

Usually, populations are large, and is unlikely we have access to the entire population to calculate the population standard deviation value.

As with most cases in research, sampling a population is a much easier and less costly approach. Fortunately, there is a way to estimate the standard error of the mean using the sample standard deviation. Here is the formula:

$SE = \frac{s}{\sqrt{n}}$

Where:

$SE$ = Standard error of the mean
$s$ = Sample standard deviation
$n$ = Sample size
$\sqrt{n}$ = Square root of the sample size

You may have noticed that both formulas for the standard error above are quite similar. Indeed they are, the only difference being whether we know the value for population standard deviation or not.

How to Calculate Standard Error

To calculate standard error, follow these simple steps:

Calculate or obtain your standard deviation (s for sample, σ for population)
Count your sample size (n)
Calculate the square root of your sample size (√n)
Divide the standard deviation by √n to get your standard error

The standard error formula is: SE = s / √n (for sample data) or SE = σ / √n (for population data).

In practice, you can calculate standard error using:

Excel: =STDEV(range)/SQRT(COUNT(range))
SPSS: Analyze → Descriptive Statistics → Explore (detailed steps below)
R: stderr <- function(x) sd(x)/sqrt(length(x)) (detailed steps below)

Now that we know the equations for standard error, let's do some basic math and learn how to calculate standard error by hand.

Example 1: Assuming we know that the actual standard deviation of a population consisting of students taking their final exam is 7. We also took a random sample of 100 respondents from this population. Therefore we have:

$\sigma = 7, \quad N = 100$

Since in this standard error example we know the actual standard deviation value, we will use the first equation for the standard error above, respectively:

$SE = \frac{\sigma}{\sqrt{n}}$

After plugging the numbers in the equation we have:

$SE = \frac{7}{\sqrt{100}} = \frac{7}{10} = 0.70$

So, how do we interpret the standard error result in this example? It simply means that when we take a random sample of N = 100 from this population, the average difference between sample means and the population mean is 0.70.

Example 2: Now, let's assume we don't know the population standard deviation of the students taking their final exam in our school. Instead, we know the sample standard deviation (S) which let's assume is 5. The sample (N) remains unchanged, respectively 100. Therefore we have:

$s = 5, \quad N = 100$

This time we will use the equation for standard sample deviation:

$SE = \frac{s}{\sqrt{n}}$

After we insert the numbers we have:

$SE = \frac{5}{\sqrt{100}} = \frac{5}{10} = 0.50$

We can interpret this result as the average difference between sample means and the population mean when the sample is randomly selected and N = 100 is 0.50.

The standard error of the mean is a measure of how much difference you expect to get between a sample statistic and the population parameter and the sample means and the population mean when samples are randomly selected and of a given size.

Calculate Standard Error in SPSS

There are numerous ways to find the standard error in SPSS. In this section, we will focus on two efficient methods.

Want to follow along? Download the practice SPSS dataset from the sidebar, then launch SPSS on your computer and navigate to File → Open → Data to import the .sav file.

(1) Calculate Standard Error of the Mean in SPSS using Explore Analysis

In SPSS top menu, navigate at Analyze → Descriptive Statistics → Explore

SPSS menu showing navigation path Analyze then Descriptive Statistics then Explore for calculating standard error Navigate to Analyze → Descriptive Statistics → Explore in SPSS

On the Explore window, select a variable in the left box and click the arrow button to add it to the Dependent List.

SPSS Explore dialog box showing variable list on left with arrow button to move variables to Dependent List Select your variable and click the arrow button to add it to the Dependent List

Click the OK button to proceed with the analysis.

SPSS Explore window with OK button highlighted ready to run standard error analysis Click OK to execute the Explore analysis

On the Output window, scroll down to the Descriptivetable. On the Meanrow, check the Std. Errorcolumn to find the standard error value for the respective variable.

In our example, the mean for the System variable is 4.10 and the standard error is 0.081.

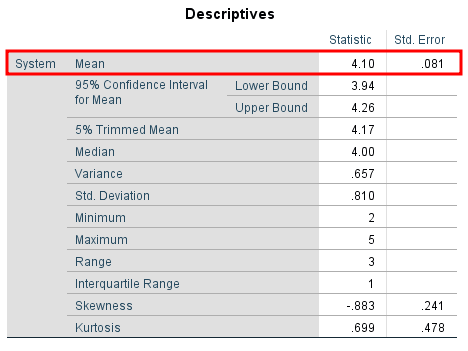SPSS Descriptives output table showing Mean of 4.10 with Std. Error of 0.081 for System variable SPSS Descriptives table showing standard error value of 0.081 in the Std. Error column

This standard error value is a fairly low one meaning that the sample means analyzed are closely distributed around the population mean. In other words, our sample is representative of the population from where was taken.

If the standard error of the mean in your analysis is high, increasing the sample size through random selection will likely decrease the standard error value.

For instance, if your sample size is N = 50, you could increase it to N = 100 or more to lower the standard error, as seen in the side-by-side comparison below.

Pay attention to the mean and standard error of the mean in both figures.

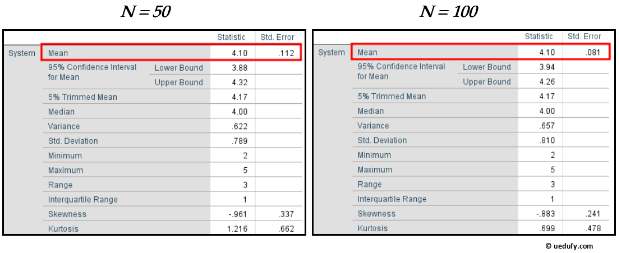Side-by-side comparison of SPSS output showing lower standard error with N=100 versus N=50 sample size Comparison showing how standard error decreases as sample size increases from N=50 to N=100

(2) Find Standard Error on the Mean in SPSS using Frequency Analysis

Another way of calculating standard error in SPSS is using the Frequency analysis. In SPSS, navigate to Analysis → Descriptive Statistics → Frequencies

SPSS menu showing navigation path Analyze then Descriptive Statistics then Frequencies for standard error calculation Navigate to Analyze → Descriptive Statistics → Frequencies in SPSS

On the Frequencies window, add the variable of interest from the left box to the Variable(s). Uncheck the Display frequency tablecheck-box and click the Statistics button.

SPSS Frequencies dialog box showing variable selection with Display frequency table unchecked and Statistics button Add your variable to Variable(s), uncheck Display frequency table, and click Statistics

On the Statistics window, make sure the S.E. mean check-box is selected, and press the Continue button.

SPSS Frequencies Statistics window with S.E. mean checkbox selected for standard error calculation Select the S.E. mean checkbox and click Continue

Click on the OK in the Frequencies window to proceed with the standard error analysis.

SPSS Frequencies window with OK button ready to execute standard error analysis 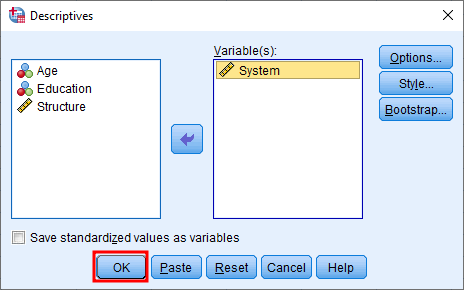Click OK to run the Frequencies analysis

The standard error value will be shown in the Std. Error of Mean row of the Statistics table

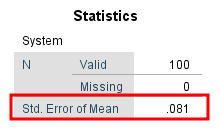SPSS Statistics output table showing Std. Error of Mean value from Frequencies analysis The standard error result appears in the Std. Error of Mean row of the Statistics table

Standard Error Calculation in Excel

To find the standard error of the mean in Excel, we simply need to translate the standard error formula into Excel syntax: standard error = standard deviation / square root of the total number of samples N.

Practice dataset available: Grab the Excel file from the sidebar to follow along with this example.

Here's how to calculate it:

On your Excel data set, click on an empty cell anywhere on your datasheet

Excel spreadsheet showing data in rows with empty cell selected for entering standard error formula Click on an empty cell in Excel where you want the standard error result to appear

Copy the standard error Excel formula below into the Insert Function field in Excel.

=STDEV(sampling range)/SQRT(COUNT(sampling range))

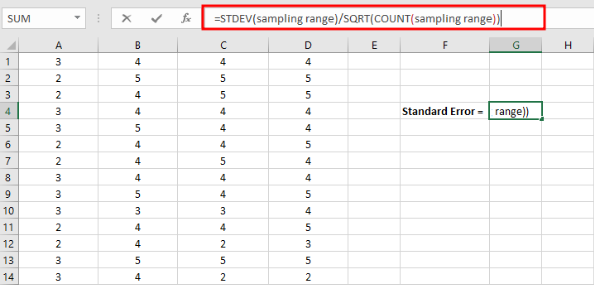Excel formula bar showing standard error formula STDEV divided by SQRT of COUNT for calculating standard error Enter the standard error formula: =STDEV(sampling range)/SQRT(COUNT(sampling range))

Replace the sampling range in the standard error Excel formula with the actual range of cells you want to include in your analysis.

Once your selection is done, hit the ENTER key to complete the analysis.

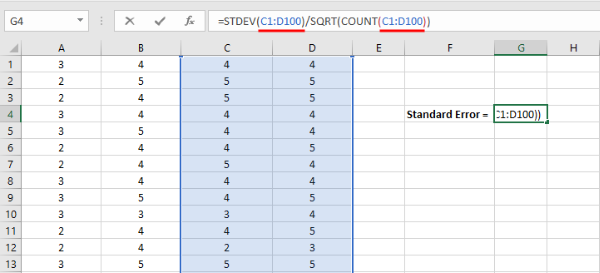Excel formula with actual cell range A2:A101 replacing sampling range placeholder in standard error calculation Replace "sampling range" with your actual cell range (e.g., A2:A101) and press ENTER

Excel will show the standard error result in the respective cell as seen in the capture below.

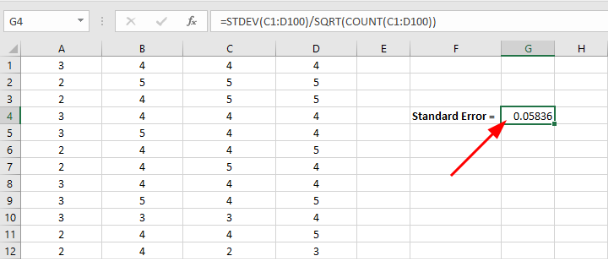Excel cell displaying calculated standard error result after executing the formula Excel displays the calculated standard error value in the selected cell

Standard Error Calculation In R

Finally, let’s have a look at which function we can use to find the standard error of the mean in R.

As we discussed earlier, the standard error of the mean is just the standard deviation divided by the square root of the sample size.

For this example I am going to use the same Excel dataset we used in the previous section.

Launch RStudio on your computer. On the R top menu, navigate to File → Import Dataset → From Excel.

On the Import Excel Data in R window, click on Browse and select the dataset.xlsx file you download above. Click Open then the Import button to finish importing the Excel dataset in R.

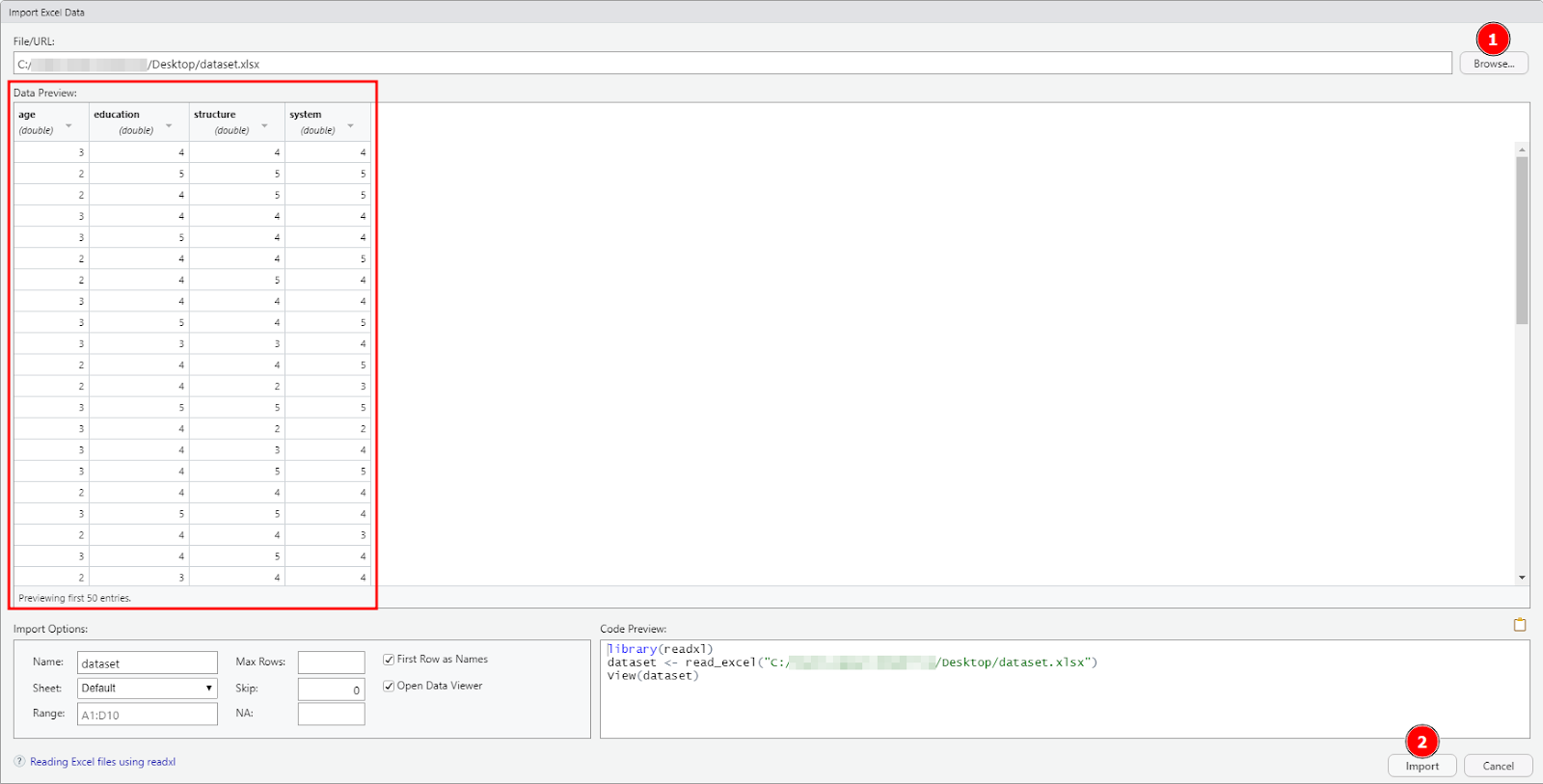RStudio Import Excel Data window showing Browse button to select dataset file and Import button to load data Click Browse to select your Excel file, then click Import to load the dataset in R

**NOTE:**R might require certain libraries to be able to import data from Excel files (.xlsx, .csv, etc.). If prompted, allow RStudio to automatically install the required dependencies.

(1) Find Standard Error in R using the Standard Error Formula

The first step is to translate the equation for standard error of the mean to a new function(x) in R. Let's call this function, e.g., stderr or any other name you want.

Type this function in the Console window in R then press ENTER.

stderr <- function(x) sd(x)/sqrt(length(x))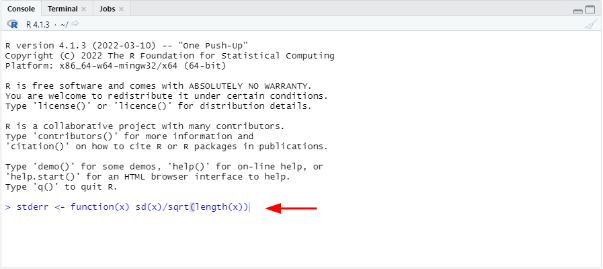

RStudio Console showing custom stderr function definition for calculating standard error using sd and sqrt in R Create a custom stderr function in R Console: stderr <- function(x) sd(x)/sqrt(length(x))

Next, let’s calculate the standard error of the mean for the age column in our dataset.

To do so, we will basically invoke the function we created and specify the dataset file and column we want to compute the standard deviation in R using the following syntax:

stderr(dataset$age)

Where:

stderr = function for standard error formula in R
dataset = the dataset file we imported in R
age = the column (variable) we want to find the standard error of the mean value

The standard error for the age variable in our dataset is 0.06 as seen in the capture below:

RStudio Console output showing standard error result of 0.06 after running stderr function on age variable The stderr(dataset$age) function returns a standard error value of 0.06

(2) Find Standard Error in R using Plotrix library

This method uses the std.error() function in the Plotrix package in R. First we need to install the Plotrix library by typing the following command in the Console window in R:

install.packages('plotrix')

Next, we need to call the Plotrix library in R using the following command:

library('plotrix')

Finally, we can use the std.error function to calculate the standard error of the mean for the system variable in our dataset.

std.error(dataset$system)

RStudio Console showing std.error function from Plotrix library calculating standard error for system variable Using Plotrix's std.error() function to calculate standard error for the system variable

Frequently Asked Questions

How to find standard error?

To find standard error, divide the standard deviation by the square root of the sample size: SE = s / √n. In Excel, use =STDEV(range)/SQRT(COUNT(range)). In SPSS, use Analyze → Descriptive Statistics → Explore and check the Mean row for Std. Error. In R, use `stderr <- function(x) sd(x)/sqrt(length(x))` then stderr(your_data).

How to calculate standard error in Excel?

To calculate standard error in Excel: (1) Click on an empty cell, (2) Enter the formula =STDEV(your_range)/SQRT(COUNT(your_range)), replacing 'your_range' with your actual cell range (e.g., A1:A100), (3) Press ENTER. Excel will calculate the standard error of the mean for your dataset.

How to find standard error in Excel?

Find standard error in Excel by using the formula =STDEV(data_range)/SQRT(COUNT(data_range)). This divides your data's standard deviation by the square root of your sample size. For example, if your data is in cells A1 to A50, use =STDEV(A1:A50)/SQRT(COUNT(A1:A50)).

What is standard error of the mean?

Standard error of the mean (SEM) measures how much sample means vary from the true population mean. It indicates the precision of your sample mean as an estimate of the population mean. A lower standard error means your sample is more representative of the population. It's calculated as the standard deviation divided by the square root of sample size.

How to calculate standard error?

Calculate standard error using the formula: SE = s / √n, where s is the standard deviation and n is the sample size. If you know the population standard deviation (σ), use SE = σ / √n. The standard error decreases as sample size increases, making your estimate more precise.

How to calculate standard error of the mean?

To calculate standard error of the mean: (1) Calculate or obtain your sample's standard deviation (s), (2) Count your sample size (n), (3) Calculate the square root of n, (4) Divide s by √n. The formula is SE = s / √n. For a sample with standard deviation of 5 and n=100, SE = 5/√100 = 5/10 = 0.5.

Standard error formula?

The standard error formula is SE = s / √n for sample standard deviation, or SE = σ / √n for population standard deviation. Where SE is standard error, s is sample standard deviation, σ is population standard deviation, and n is sample size. This formula shows that standard error decreases as sample size increases.

How to interpret standard error?

Interpret standard error as a measure of sampling precision: Lower values indicate sample means are tightly clustered around the population mean (more precise estimate). Higher values suggest greater variability between samples (less precise estimate). A standard error of 0.5 means sample means typically vary by about 0.5 units from the true population mean.

Standard error vs standard deviation?

Standard deviation measures variability of individual data points within your sample. Standard error measures how much your sample mean varies from the true population mean. Standard deviation stays relatively constant regardless of sample size, while standard error decreases as sample size increases. SE = SD / √n shows this relationship.

What is a good standard error of the mean?

There's no universal 'good' standard error value - it depends on your data's scale and research context. Generally, smaller is better as it indicates more precision. Compare standard error to your mean: if SE is 1 and mean is 100, that's 1% variability (good). If SE is 10 and mean is 20, that's 50% variability (concerning). Increase sample size to reduce standard error.

Wrapping Up

The standard error of the mean measures the difference between the sample means compared with the mean of the true population. In other words, it tells us whether our sample is representative of the population from which it was taken.

If the sample analysis shows a high standard error, the best way to lower it is by increasing the sample size using random data collection.

Related Topics: If you're working with survey or questionnaire data, you might also need to assess reliability using Cronbach's Alpha in Excel or Cronbach's Alpha in SPSS to ensure your measurement scales are consistent before calculating descriptive statistics like standard error.

References

Field, A., Miles, J., & Field, Z. (2012).Discovering statistics using R. SAGE Publications.

Field, A. (2013).Discovering statistics using IBM SPSS statistics (4th ed.). SAGE Publications.

McNeil, E. (2020). Data management and visualization using R.– Songkhla: Epidemiology Unit, Faculty of Medicine, Prince of Songkla University, 2020.