Linearity ในสถิติคืออะไร? คุณเคยสังเกตเห็น Scatter Plot ที่มีรูปแบบของข้อมูลเป็นเส้นตรงหรือไม่? นั่นคือจุดที่ Linearity ในสถิติเข้ามามีบทบาท ในบทความนี้ เราจะสำรวจความหมายของ Linearity วิธีการทดสอบ Linearity และอภิปรายความสำคัญของมันใน Regression Analysis, Correlation และวิธีการทางสถิติอื่นๆ
พื้นฐาน: Linearity ในสถิติคืออะไร?
Linearity ในสถิติเกี่ยวข้องกับความสัมพันธ์ระหว่างตัวแปร แต่ไม่ใช่ความสัมพันธ์ทั่วไป เรากำลังพูดถึงความสัมพันธ์ที่การเปลี่ยนแปลงในตัวแปรหนึ่งสอดคล้องโดยตรงกับการเปลี่ยนแปลงในอีกตัวแปรหนึ่ง ลองนึกภาพเส้นตรงที่เชื่อมต่อสองจุดบนกราฟ นั่นคือ Linear Relationship ในทางปฏิบัติ: ยิ่งเส้นตรงมากเท่าไร ความสัมพันธ์ระหว่างตัวแปรก็ยิ่ง "linear" มากขึ้นเท่านั้น
ตัวอย่างง่ายๆ ของ Linear Relationship คือความเชื่อมโยงระหว่างระยะทางที่คุณเดินทางกับเวลาที่ใช้ในการไปถึงที่นั่น หากคุณเดินทางด้วยความเร็วคงที่ ความสัมพันธ์ระหว่างระยะทางและเวลาจะเป็นแบบ Linear ซึ่งหมายความว่าหากคุณเพิ่มเวลาเป็นสองเท่า คุณก็จะเพิ่มระยะทางเป็นสองเท่าเช่นกัน
เมื่อต้องจัดการกับ Linearity ในสถิติ เรามักแสดงความสัมพันธ์ระหว่างตัวแปรโดยใช้สมการเชิงเส้น ในกรณีที่ง่ายที่สุด ที่เกี่ยวข้องกับสองตัวแปร (x และ y) ความสัมพันธ์เชิงเส้นสามารถแสดงด้วยสมการ:
ในที่นี้ m แสดงถึง Slope (อัตราการเปลี่ยนแปลง) ของเส้น, b คือ y-intercept (ค่าของ y เมื่อ x = 0) และ x และ y คือตัวแปรอิสระและตัวแปรตามตามลำดับ คุณสามารถคิดถึง Slope ว่าเป็น "ความชัน" ของเส้น ในขณะที่ y-intercept คือจุดที่เส้นตัดแกน y
มาลงรายละเอียดในตัวอย่าง สมมติว่าคุณต้องการทำนายราคาของพิซซ่าตามขนาด (เป็นนิ้ว) คุณรวบรวมข้อมูลบางส่วนและค้นพบว่าความสัมพันธ์ระหว่างขนาด (x) และราคา (y) เป็นแบบ Linear โดยมี Slope (m) เท่ากับ 2 และ y-intercept (b) เท่ากับ 5 สมการเชิงเส้นของคุณจะมีลักษณะดังนี้:
ตอนนี้ หากคุณต้องการทราบราคาของพิซซ่าขนาด 12 นิ้ว ให้แทนค่าสำหรับ x:
ดังนั้น พิซซ่าขนาด 12 นิ้วจะมีราคา $29
เหตุใดเราจึงควรให้ความสำคัญกับ Linearity?
Linearity เป็นรากฐานของเทคนิคทางสถิติหลายๆ ประเภทที่ช่วยให้เราเข้าใจแนวโน้ม รูปแบบ และความสัมพันธ์ระหว่างตัวแปร มันมีความสำคัญอย่างยิ่งในสาขาเช่น สังคมศาสตร์ เศรษฐศาสตร์ และวิทยาศาสตร์ธรรมชาติ มาเจาะลึกเหตุผลบางประการว่าทำไม Linearity จึงสำคัญมาก:
1. Regression Analysis
หนึ่งในการใช้งาน Linearity ที่พบบ่อยที่สุดคืออยู่ใน Regression Analysis การวิเคราะห์ Regression เกี่ยวกับการหารูปแบบทางคณิตศาสตร์ที่เหมาะสมที่สุดกับชุดข้อมูล เมื่อมี Linear Relationship ระหว่างตัวแปร เราสามารถใช้เทคนิคที่เรียกว่า Linear Regression เพื่อหาเส้นที่เหมาะสมที่สุด
หากเราสมมติว่ามี Linear Relationship ระหว่างตัวแปร แต่แท้จริงแล้วไม่มี เราอาจไม่ได้ผลลัพธ์ที่แม่นยำ เราอาจได้แบบจำลองที่ไม่อธิบายพฤติกรรมของตัวแปรที่เราสนใจ หรือเราอาจทำการทำนายที่คลาดเคลื่อนอย่างมาก
ตัวอย่างเช่น สมมติว่าเรากำลังสำรวจว่าอุณหภูมิส่งผลต่อการเจริญเติบโตของพืชอย่างไร เราสมมติว่ามี Linear Relationship ระหว่างอุณหภูมิและการเจริญเติบโต ดังนั้นเราใช้ Linear Regression เพื่อทำการทำนาย แต่หากความสัมพันธ์ระหว่างอุณหภูมิและการเจริญเติบโตเป็นแบบ Non-linear (บางทีอาจมีอุณหภูมิที่เหมาะสมที่สุดที่การเจริญเติบโตสูงที่สุด ทำให้เกิดความสัมพันธ์แบบโค้ง) แล้วแบบจำลอง Linear Regression ของเราอาจไม่แม่นยำ เราอาจทำการทำนายที่ไม่สะท้อนผลลัพธ์ในโลกแห่งความจริง
นั่นคือเหตุผลที่การทดสอบ Linearity ก่อนดำเนินการ Linear Regression มีความสำคัญ เราจำเป็นต้องตรวจสอบว่าความสัมพันธ์ระหว่างตัวแปรเป็นแบบ Linear ก่อนที่เราจะสมมติว่าเป็นเช่นนั้น หากไม่มี Linear Relationship เราอาจต้องแปลงข้อมูลหรือใช้แบบจำลองอื่นเพื่อจับพฤติกรรมของตัวแปรได้อย่างแม่นยำ
การทดสอบ Linearity ใน Regression ทำให้เรามั่นใจได้ว่าผลลัพธ์ Linear Regression ของเราสะท้อนความสัมพันธ์ระหว่างตัวแปรที่เราสนใจได้อย่างแม่นยำ
2. Correlation
อีกเหตุผลหนึ่งที่ต้องให้ความสำคัญกับ Linearity คือมันมีความสำคัญต่อการทำความเข้าใจ Correlation การวัด Correlation เป็นการวัดว่าสองตัวแปรมีความสัมพันธ์กันแน่นแฟ้นเพียงใด เมื่อความสัมพันธ์ระหว่างตัวแปรเป็นแบบ Linear ค่าสัมประสิทธิ์สหสัมพันธ์ (มักแสดงด้วย "r" หรือ "rho") สามารถให้ข้อมูลเชิงลึกที่มีค่าเกี่ยวกับความแข็งแกร่งและทิศทางของความสัมพันธ์
ค่าสัมประสิทธิ์สหสัมพันธ์ของ +1 บ่งชี้ถึง Perfect Positive Linear Relationship ในขณะที่ค่าสัมประสิทธิ์สหสัมพันธ์ของ -1 หมายถึง Perfect Negative Linear Relationship ค่าสัมประสิทธิ์สหสัมพันธ์ของ 0 จะบ่งชี้ว่าไม่มี Linear Relationship
ตัวอย่างเช่น สมมติว่าคุณต้องการทราบว่ามีความสัมพันธ์ระหว่างจำนวนชั่วโมงที่นักเรียนศึกษากับคะแนนสอบของพวกเขาหรือไม่ โดยการคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ คุณสามารถกำหนดความแข็งแกร่งและทิศทางของ Linear Relationship ระหว่างสองตัวแปรนี้
3. Analysis of Covariance (ANCOVA) และ Mixed Models
ในขณะที่ ANOVA มาตรฐานไม่ต้องการสมมติฐาน Linearity (เนื่องจากมันเปรียบเทียบค่าเฉลี่ยระหว่างกลุ่มตามหมวดหมู่) Linearity จะกลายเป็นสิ่งสำคัญเมื่อเราขยาย ANOVA ไปสู่แบบจำลองที่ซับซ้อนมากขึ้นเช่น ANCOVA (Analysis of Covariance) หรือเมื่อรวม Continuous Covariates
ใน ANCOVA เราตรวจสอบความแตกต่างของกลุ่มในขณะที่ควบคุม Continuous Covariates สมมติฐาน Linearity ระบุว่าความสัมพันธ์ระหว่าง Covariate และตัวแปรตามต้องเป็นแบบ Linear ในทุกกลุ่มที่กำลังเปรียบเทียบ
ตัวอย่างเช่น สมมติว่าเรากำลังเปรียบเทียบคะแนนทดสอบของสามวิธีการสอน (A, B และ C) ในขณะที่ควบคุมคะแนนความรู้พื้นฐานของนักเรียน เราจำเป็นต้องตรวจสอบว่าความสัมพันธ์ระหว่างความรู้พื้นฐานและคะแนนทดสอบเป็นแบบ Linear สำหรับทั้งสามกลุ่มวิธีการสอน
หากความสัมพันธ์ระหว่าง Covariate และตัวแปรตามเป็นแบบ Non-linear (บางทีอาจโค้งหรือแสดงรูปแบบที่แตกต่างกันในแต่ละกลุ่ม) ผลลัพธ์ ANCOVA อาจมีอคติ ค่าเฉลี่ยที่ปรับแล้วจะถูกประมาณอย่างไม่ถูกต้อง ซึ่งอาจนำไปสู่ข้อสรุปที่ผิดพลาดเกี่ยวกับความแตกต่างของกลุ่ม
เมื่อ Linearity ถูกละเมิดใน ANCOVA เรามีหลายทางเลือก: แปลง Covariate เพื่อให้ได้ Linearity, ใช้ Polynomial Terms เพื่อจำลอง Non-linear Relationships หรือใช้แนวทางการวิเคราะห์ทางเลือกเช่น Nonparametric Methods การตรวจสอบ Linearity ก่อนดำเนินการ ANCOVA ทำให้เรามั่นใจว่าผลลัพธ์ของเราสะท้อนความแตกต่างของกลุ่มที่แท้จริงหลังจากพิจารณา Covariates อย่างแม่นยำ
4. Hypothesis Testing
ในสถิติ Hypothesis Testing เป็นวิธีการกำหนดว่าสองตัวแปรมีความสัมพันธ์กันหรือไม่ เรามักเริ่มต้นโดยสมมติว่าไม่มีความสัมพันธ์ระหว่างตัวแปรที่เรากำลังตรวจสอบ (สิ่งนี้เรียกว่า Null Hypothesis) จากนั้นเรารวบรวมข้อมูลและทำการคำนวณเพื่อกำหนดว่ามีหลักฐานเพียงพอที่จะปฏิเสธ Null Hypothesis และสรุปว่ามีความสัมพันธ์ระหว่างตัวแปรหรือไม่
อย่างไรก็ตาม หากเราสมมติว่ามี Linear Relationship ระหว่างตัวแปรเมื่อไม่มี เราอาจปฏิเสธ Null Hypothesis เมื่อเราไม่ควรทำ นั่นคือจุดที่ Linearity เข้ามา เราจำเป็นต้องตรวจสอบว่ามี Linear Relationship ระหว่างตัวแปรที่เรากำลังทดสอบก่อนดำเนินการ Hypothesis Testing
ตัวอย่างเช่น สมมติว่าเรากำลังทดสอบว่ามีความสัมพันธ์ระหว่างจำนวนชั่วโมงที่ใครบางคนออกกำลังกายต่อสัปดาห์กับระดับคอเลสเตอรอลของพวกเขาหรือไม่ หากมี Linear Relationship ระหว่างตัวแปรเหล่านี้ เราสามารถใช้ Hypothesis Testing เพื่อกำหนดว่ามีหลักฐานเพียงพอที่จะสรุปว่าการออกกำลังกายมากขึ้นนำไปสู่ระดับคอเลสเตอรอลที่ต่ำลงหรือไม่
แต่หากความสัมพันธ์ระหว่างการออกกำลังกายและคอเลสเตอรอลเป็นแบบ Non-linear (บางทีอาจโค้งหรือแสดงผลลดหลั่น) การทดสอบสมมติฐานของเราอาจไม่แม่นยำ เราอาจปฏิเสธ Null Hypothesis และสรุปว่ามีความสัมพันธ์ระหว่างตัวแปรเมื่อความสัมพันธ์ไม่ตามรูปแบบ Linear ที่เราสมมติ
5. Design of Experiments
ในสถิติ การออกแบบการทดลองช่วยให้เรากำหนดว่าตัวแปรต่างๆ ส่งผลต่อผลลัพธ์อย่างไร ตัวอย่างเช่น หากเรากำลังสำรวจว่าปัจจัยใดส่งผลต่อการเจริญเติบโตของพืช เราอาจจัดการตัวแปรเช่นแสง น้ำ และปุ๋ยเพื่อสังเกตผลกระทบของพวกมันต่อพืช
ในการออกแบบการทดลองหลายๆ แบบ เราสมมติว่าผลของแต่ละตัวแปรต่อผลลัพธ์เป็นแบบ Linear นั่นคือจุดที่ Linearity เข้ามา เราจำเป็นต้องตรวจสอบว่าความสัมพันธ์ระหว่างตัวแปรและผลลัพธ์เป็นแบบ Linear ก่อนออกแบบการทดลองของเรา
หากเราสมมติว่ามี Linear Relationship ระหว่างตัวแปรและผลลัพธ์เมื่อไม่มี เราอาจไม่ได้ผลลัพธ์ที่เราต้องการ เราอาจจัดการตัวแปรและไม่สังเกตผลต่อผลลัพธ์ หรือเราอาจเห็นผลที่แตกต่างจากที่คาดหวัง
ตัวอย่างเช่น สมมติว่าเรากำลังสำรวจว่าระดับแสงที่แตกต่างกันส่งผลต่อการเจริญเติบโตของพืชอย่างไร เราสมมติว่ามี Linear Relationship ระหว่างแสงและการเจริญเติบโต ดังนั้นเราออกแบบการทดลองของเราเพื่อทดสอบระดับแสงที่แตกต่างกัน แต่หากความสัมพันธ์ระหว่างแสงและการเจริญเติบโตเป็นแบบ Non-linear (บางทีการเจริญเติบโตอาจคงที่หลังจากเกณฑ์บางอย่าง) การทดลองของเราอาจไม่แม่นยำ เราอาจจัดการแสงและไม่สังเกตผลเพิ่มเติมต่อการเจริญเติบโต หรือเราอาจเห็นรูปแบบที่แตกต่างจากที่คาดหวัง
การทดสอบ Linearity ก่อนออกแบบการทดลองมีความสำคัญอย่างยิ่ง เราจำเป็นต้องตรวจสอบว่าผลของแต่ละตัวแปรต่อผลลัพธ์เป็นแบบ Linear ก่อนที่เราจะสมมติว่าเป็นเช่นนั้น หากไม่มี Linear Relationship เราอาจต้องใช้การออกแบบการทดลองหรือแบบจำลองที่แตกต่างกันเพื่อจับพฤติกรรมของตัวแปรได้อย่างแม่นยำ
เกิดอะไรขึ้นเมื่อ Linearity ถูกละเมิด?
มันมีความสำคัญอย่างยิ่งที่จะตรวจสอบว่าเรามี Linear Relationship ก่อนใช้แบบจำลอง Linear Regression หากเราไม่ทำ การทำนายของเราจะไม่แม่นยำ และเราอาจไม่ได้ผลลัพธ์ที่เราต้องการ การละเมิดสมมติฐาน Linearity อาจนำเราไปสู่การระบุความสัมพันธ์ที่ไม่มีอยู่จริง นั่นคือเหตุผลที่เราจำเป็นต้องทดสอบ Linearity ก่อนทำการทำนาย
หากเราละเมิดสมมติฐาน Linearity เราอาจได้ผลลัพธ์ที่มีอคติอย่างมาก ตัวอย่างเช่น หากเรากำลังพยายามทำนายราคาบ้านตามพื้นที่ตารางเมตร เราอาจสมมติว่าเราสามารถใช้แบบจำลอง Linear ได้ แต่หากความสัมพันธ์ระหว่างราคาบ้านและพื้นที่ตารางเมตรไม่เป็นแบบ Linear (บางทีราคาอาจเพิ่มขึ้นแบบทวีคูณเมื่อพื้นที่ตารางเมตรเพิ่มขึ้น) แบบจำลอง Linear Regression ของเราจะให้การทำนายที่ไม่แม่นยำ
นั่นคือเหตุผลที่การทดสอบ Linearity ก่อนใช้แบบจำลอง Linear Regression มีความสำคัญอย่างยิ่ง หากเราไม่ทำ เราอาจได้การทำนายที่มีอคติ การประมาณค่าสัมประสิทธิ์ที่ไม่ถูกต้อง หรือผลลัพธ์ที่ทำให้เข้าใจผิดโดยรวม โดยการใช้เวลาในการตรวจสอบ Linearity เราสามารถมั่นใจได้ว่าแบบจำลองของเราสะท้อนความสัมพันธ์ในโลกแห่งความจริงอย่างแม่นยำและให้ข้อมูลเชิงลึกที่ถูกต้องเกี่ยวกับปรากฏการณ์ที่เรากำลังสำรวจ
วิธีการทดสอบ Linearity ในสถิติ?
เมื่อเข้าใจว่า Linearity มีความสำคัญ เราจะทดสอบมันได้อย่างไร? มีหลายวิธีที่เราสามารถใช้:
1. Scatterplots
Scatterplot เป็นกราฟที่แสดงความสัมพันธ์ระหว่างสองตัวแปร หากมี Linear Relationship จุดบน Scatterplot จะสร้างรูปแบบที่ใกล้เคียงกับเส้นตรง
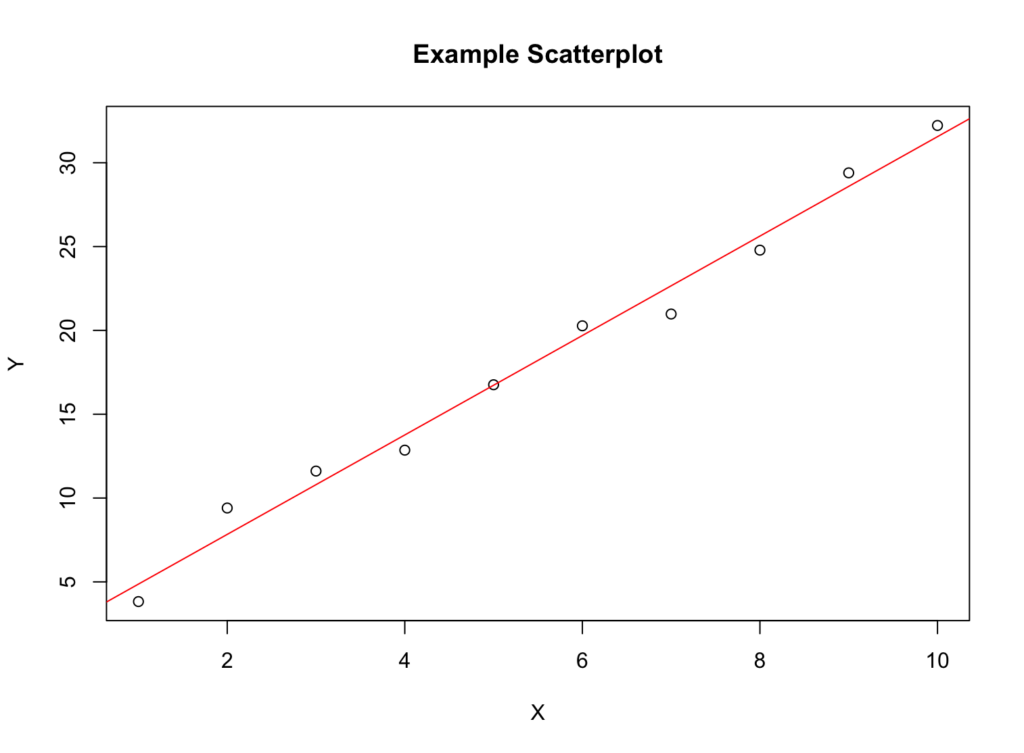รูปที่ 1: ตัวอย่าง Scatterplot แสดง Linear Relationship
2. Correlation Coefficient
ค่าสัมประสิทธิ์สหสัมพันธ์วัดความแข็งแกร่งและทิศทางของ Linear Relationship ระหว่างสองตัวแปร หากมี Linear Relationship ค่าสัมประสิทธิ์สหสัมพันธ์จะใกล้เคียง 1 (หรือ -1 สำหรับความสัมพันธ์เชิงลบ) ตัวอย่างเช่น ค่าสัมประสิทธิ์สหสัมพันธ์ 0.9975 บ่งชี้ว่ามี Positive Linear Relationship ที่แข็งแกร่งมากระหว่างตัวแปร
3. Residual Plots
Residual Plot แสดงความแตกต่างระหว่างค่าที่สังเกตและค่าที่ทำนายจากแบบจำลอง Regression ของเรา หากมีการกระจายของจุดแบบสุ่มโดยไม่มีรูปแบบที่เห็นได้ชัด สมมติฐาน Linearity น่าจะถูกต้อง อย่างไรก็ตาม หากมีรูปแบบ (เช่น รูปแบบโค้งหรือรูปแบบกรวย) แบบจำลอง Linear ของเราอาจไม่เหมาะสม
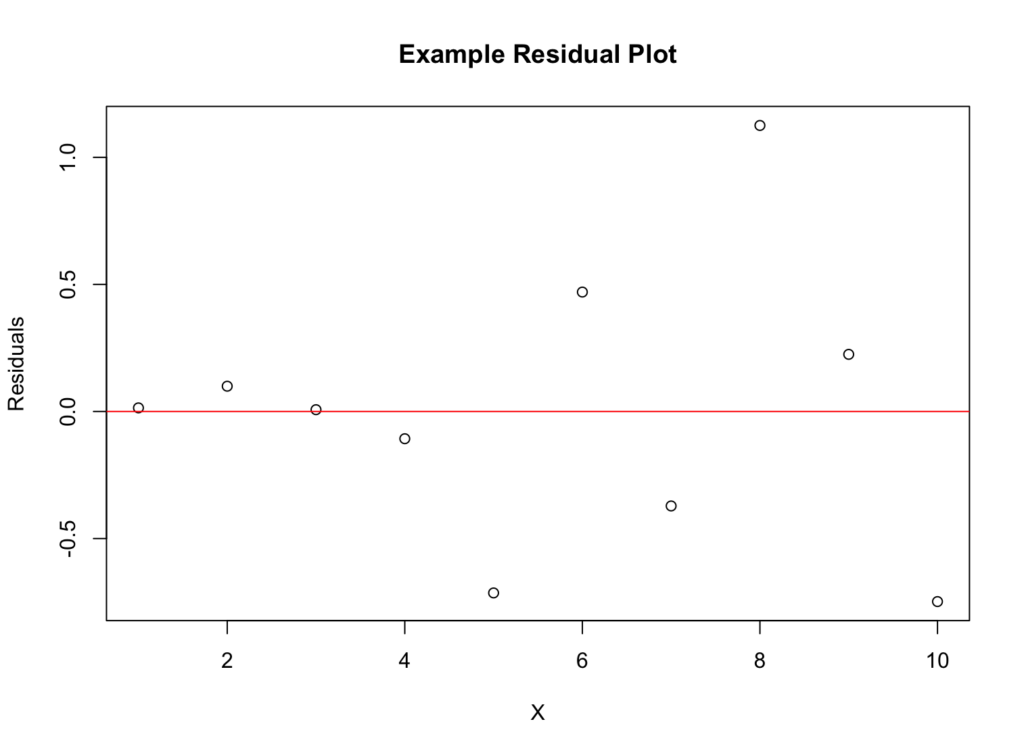รูปที่ 2: Residual Plot สำหรับการประเมิน Linearity
การอ่านค่า / การแปลผล
การแปลผลการทดสอบ Linearity ต้องพิจารณาจากหลายแหล่งข้อมูล:
Scatterplot: จุดควรสร้างรูปแบบที่ใกล้เคียงกับเส้นตรง หากจุดสร้างรูปแบบโค้ง U-shape หรือรูปแบบอื่นที่ไม่เป็นเส้นตรง แสดงว่าอาจมีปัญหา Non-linearity
Correlation Coefficient: ค่าที่ใกล้เคียง +1 หรือ -1 บ่งชี้ว่ามี Linear Relationship ที่แข็งแกร่ง ค่าระหว่าง 0.7-1.0 (หรือ -0.7 ถึง -1.0) มักถือว่าเป็นความสัมพันธ์ที่แข็งแกร่ง
Residual Plot: ต้องการเห็นการกระจายแบบสุ่ม หากเห็นรูปแบบใดๆ เช่น:
- รูปแบบโค้ง (Curved pattern) - แสดงว่าความสัมพันธ์เป็นแบบ Non-linear
- รูปแบบกรวย (Funnel shape) - แสดงปัญหา Heteroscedasticity แต่อาจยังมีปัญหา Linearity ด้วย
- U-shape หรือ Inverted U-shape - แสดงว่าความสัมพันธ์อาจเป็นแบบ Quadratic
โดยการใช้วิธีการวินิจฉัยเหล่านี้ เราสามารถกำหนดว่ามี Linear Relationship ระหว่างสองตัวแปรหรือไม่ หากมี เราสามารถใช้แบบจำลอง Linear Regression เพื่อทำการทำนาย หากไม่มี เราจะต้องแปลงข้อมูลของเราเพื่อให้ได้ Linearity หรือใช้แนวทางการจำลองที่แตกต่างกัน (เช่น Polynomial Regression หรือ Nonlinear Models)
คำถามที่พบบ่อย
สรุป
โดยสรุป Linearity เป็นแนวคิดพื้นฐานในสถิติ ไม่ว่าคุณจะทำการวิเคราะห์ Linear Regression, ทำ ANCOVA หรือทดสอบสมมติฐาน คุณต้องตรวจสอบว่ามี Linear Relationship ระหว่างตัวแปรที่คุณกำลังตรวจสอบ
โดยการทดสอบ Linearity โดยใช้ Scatterplots, ค่าสัมประสิทธิ์สหสัมพันธ์ และ Residual Plots คุณสามารถหลีกเลี่ยงผลลัพธ์ที่มีอคติและมั่นใจว่าข้อสรุปทางสถิติของคุณถูกต้อง การทำความเข้าใจว่า Linearity หมายความว่าอย่างไรและวิธีการทดสอบ Linearity เป็นทักษะที่จำเป็นสำหรับนักวิเคราะห์ข้อมูลหรือนักวิจัยที่ทำงานกับข้อมูลเชิงปริมาณ อย่าลืมประเมินสมมติฐาน Linearity เสมอก่อนใช้แบบจำลอง Linear กับข้อมูลของคุณ