Measure of Central Tendency คืออะไร? ค่ากลางทางสถิติ Mean, Median, Mode [คู่มือฉบับสมบูรณ์]

•By Leonard Cucos•th
สถิติสถิติเชิงพรรณนา

Measure of Central Tendency เป็นแนวคิดทางสถิติพื้นฐานที่ช่วยให้คุณเข้าใจค่าทั่วไปหรือค่ากลางในชุดข้อมูล ในคู่มือนี้ คุณจะได้เรียนรู้ทั้งสามมาตรการหลัก (Mean, Median และ Mode) วิธีคำนวณแต่ละค่า และเมื่อใดควรใช้ในการวิเคราะห์ทางสถิติของคุณ

ผลการเรียนรู้

เมื่อจบบทความนี้ คุณควรจะสามารถ:

  • เข้าใจแนวคิดของ Measure of Central Tendency และความสำคัญในสถิติและการวิเคราะห์ข้อมูล

  • นิยามและแยกแยะความแตกต่างระหว่าง Mean, Median และ Mode ในฐานะ Measure of Central Tendency

  • อธิบายสูตรและขั้นตอนในการคำนวณ Mean, Median และ Mode

  • รู้จักความแตกต่างในความไวต่อค่าผิดปกติ (Outliers) และการประยุกต์ใช้ระหว่าง Mean, Median และ Mode

  • ตีความ Histogram และระบุตำแหน่งของ Mean, Median และ Mode ในการแจกแจงข้อมูล

Measure of Central Tendency คืออะไร?

โดยสรุป Measure of Central Tendency คือค่าเดียวที่แทนจุดศูนย์กลางหรือค่าที่เป็นตัวแทนของชุดข้อมูล เป็นวิธีการสรุปข้อมูลจำนวนมากด้วยตัวเลขเพียงตัวเดียว Measure of Central Tendency ช่วยให้เราเข้าใจพฤติกรรมทั่วไปหรือแนวโน้มของชุดข้อมูล ทำให้ง่ายต่อการสรุปข้อสรุปและตัดสินใจจากข้อมูล

มี Measure of Central Tendency หลักสามตัว ได้แก่ Mean, Median และ Mode มาสำรวจแต่ละตัวให้ละเอียดยิ่งขึ้น

1. Mean: ค่าเฉลี่ยเลขคณิต

Mean หรือที่เรียกว่า ค่าเฉลี่ย เป็น Measure of Central Tendency ที่นิยมใช้มากที่สุด คำนวณโดยการบวกข้อมูลทั้งหมดในชุดข้อมูลแล้วหารด้วยจำนวนข้อมูลทั้งหมด นี่คือสูตร Mean:

xˉ=1n∑i=1nxi\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i

โดยที่:

  • x̄: สัญลักษณ์นี้แทน Mean (ค่าเฉลี่ย) ของชุดข้อมูล

  • n: แทนจำนวนข้อมูลทั้งหมดในชุดข้อมูล

  • xᵢ: แทนข้อมูลแต่ละตัวในชุดข้อมูล โดย i คือดัชนีตั้งแต่ 1 ถึง n

  • Σ (จาก i=1 ถึง n): เป็นสัญลักษณ์การรวม ซึ่งบ่งชี้ว่าเราควรรวมค่าของ xᵢ สำหรับดัชนีทั้งหมดตั้งแต่ 1 ถึง n กล่าวคือ บวกข้อมูลทั้งหมดในชุดข้อมูล

เมื่อเรามองหาการแสดงผลแบบกราฟของ Mean เราควรได้สิ่งที่คล้ายกับ Histogram ด้านล่าง ในที่นี้ เราสร้างชุดข้อมูล 100 ตัวเลขสุ่มที่มี Mean เท่ากับ 50 และ Standard Deviation เท่ากับ 10

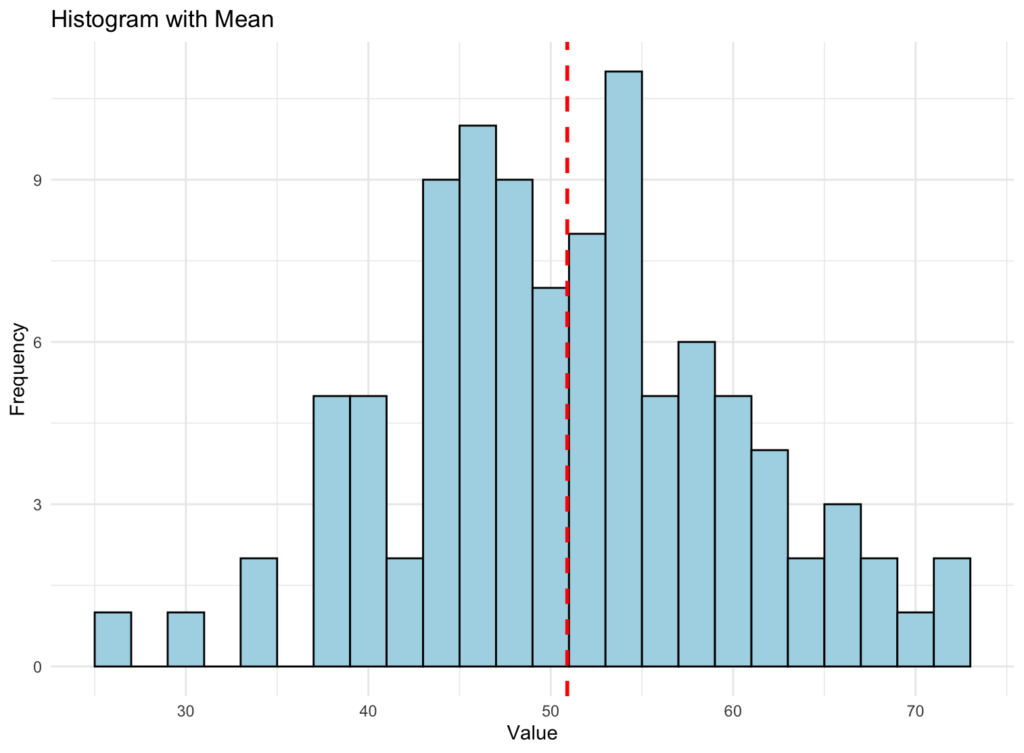
Histogram แสดงค่า Mean ของชุดข้อมูล พร้อมเส้นสีแดงประแสดงตำแหน่งค่าเฉลี่ย

Histogram แสดงการแจกแจงข้อมูลพร้อมเส้นประสีแดงที่แสดงตำแหน่งค่า Mean

หมายเหตุ:

  • Histogram คือการแสดงภาพของชุดข้อมูล มันแบ่งข้อมูลออกเป็นช่วง (Bins) จำนวนหนึ่ง และความสูงของแต่ละแท่งใน Histogram แสดงความถี่ (จำนวนครั้ง) ที่ข้อมูลตกอยู่ในช่วงเฉพาะนั้น กล่าวคือ แท่งที่สูงกว่าบ่งชี้ว่ามีข้อมูลมากกว่าในช่วงค่านั้น

  • เส้นสีแดงประในกราฟด้านบนแทนค่า Mean ของชุดข้อมูล Mean คำนวณโดยการบวกข้อมูลทั้งหมดแล้วหารด้วยจำนวนข้อมูลทั้งหมด ให้ความคิดเกี่ยวกับแนวโน้มกลาง (Central Tendency) หรือ "ค่าเฉลี่ย" ของข้อมูล

เมื่อคุณดูกราฟ คุณสามารถเห็นว่าข้อมูลถูกกระจายอย่างไร และเส้นแนวตั้งช่วยให้คุณระบุว่าค่า Mean อยู่ที่ไหนภายในการแจกแจงนั้น สิ่งนี้สามารถให้ความรู้สึกทั่วไปเกี่ยวกับแนวโน้มโดยรวมในข้อมูลและช่วยให้คุณเข้าใจพฤติกรรมของชุดข้อมูลได้ดีขึ้น

อย่างไรก็ตาม สิ่งสำคัญคือต้องจำไว้ว่า Mean อาจไวต่อ Outliers (ค่าผิดปกติ) ซึ่งอาจทำให้ Mean เบี่ยงเบนและทำให้เป็นตัวแทนของ Central Tendency ของชุดข้อมูลได้น้อยลง

เรียนรู้วิธีคำนวณ Mean ด้วยมือ Excel และ R ในไม่กี่ขั้นตอนง่ายๆ

2. Median: ค่ากลาง

Median คือค่ากลางในชุดข้อมูลเมื่อข้อมูลถูกเรียงลำดับจากน้อยไปมากหรือมากไปน้อย เปรียบเสมือนลูกคนกลางของ Central Tendency ที่มักถูกมองข้ามแต่ยังคงสำคัญมาก

เพื่อหา Median ให้เรียงลำดับชุดข้อมูลจากน้อยไปมากหรือมากไปน้อยก่อน หากมีข้อมูลจำนวนคี่ Median คือค่ากลาง หากมีข้อมูลจำนวนคู่ Median คือค่าเฉลี่ยของสองค่ากลาง นี่คือตัวอย่างรวดเร็ว:

สำหรับชุดข้อมูล:

2,4,6,8,102, 4, 6, 8, 10

Median คือ 6 เพราะเป็นค่ากลาง

สำหรับชุดข้อมูล:

2,4,6,82, 4, 6, 8

Median คือ 5 เพราะเป็นค่าเฉลี่ยของ 4 และ 6 ซึ่งเป็นสองค่ากลาง

สิ่งดีอย่างหนึ่งเกี่ยวกับ Median คือไม่ไวต่อค่าสุดขั้ว ซึ่งหมายความว่าสามารถแทนจุดศูนย์กลางได้ดีกว่าสำหรับการแจกแจงที่เบ้ (Skewed Distributions)

นี่คือการแสดงแบบกราฟของ Median โดยใช้เกณฑ์ชุดข้อมูลเดียวกันที่เราใช้ก่อนหน้านี้:

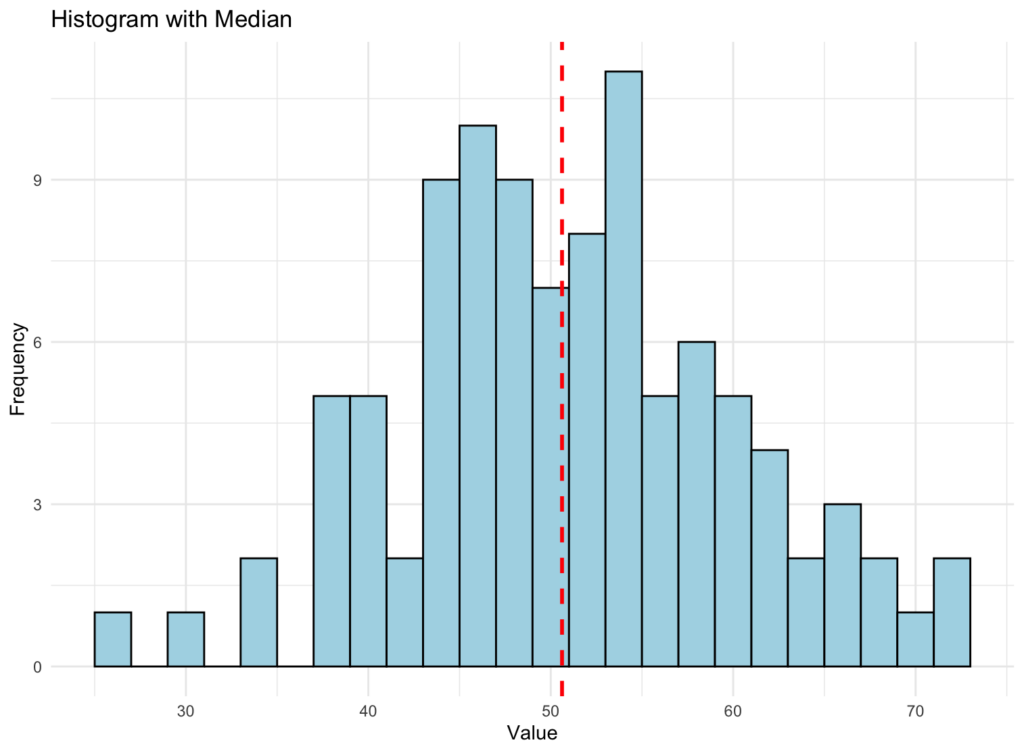
Histogram แสดงค่า Median ของชุดข้อมูล พร้อมเส้นสีแดงประแสดงตำแหน่งค่ามัธยฐาน

Histogram แสดงการแจกแจงข้อมูลพร้อมเส้นประสีแดงที่แสดงตำแหน่งค่า Median

Histogram ของ Median ด้านบนอาจดูคล้ายกับที่เราสร้างสำหรับ Mean แต่ถ้าคุณสังเกตดีๆ เส้นสีแดงประที่แทน Median จะเบี่ยงเบนไปเล็กน้อย นี่คือคำอธิบายว่าทำไม:

  • Mean (ค่าเฉลี่ย) คำนวณโดยการบวกข้อมูลทั้งหมดแล้วหารด้วยจำนวนข้อมูลทั้งหมด ให้ความคิดเกี่ยวกับแนวโน้มกลางหรือ "ค่าเฉลี่ย" ของข้อมูล อย่างไรก็ตาม Mean อาจไวต่อ Outliers (ค่าผิดปกติ) และอาจไม่แทนศูนย์กลางที่แท้จริงของชุดข้อมูลเมื่อมี Outliers

  • Median คือค่ากลางของชุดข้อมูลที่แทนด้วยเส้นสีแดงประเมื่อข้อมูลถูกเรียงลำดับจากน้อยไปมากหรือมากไปน้อย หากมีข้อมูลจำนวนคู่ Median คือค่าเฉลี่ยของสองค่ากลาง Median ไม่ไวต่อ Outliers เท่ากับ Mean และสามารถแทนแนวโน้มกลางของชุดข้อมูลได้ดีกว่าเมื่อมี Outliers

หมายเหตุ: ใน Histogram ที่สร้างขึ้น เส้นแนวตั้งสำหรับ Mean และ Median แตกต่างกันเล็กน้อยเพราะพวกมันแทน Measure of Central Tendency ที่แตกต่างกัน ตำแหน่งของพวกมันอาจแตกต่างกันขึ้นอยู่กับการแจกแจงของข้อมูลในชุดข้อมูล ในบางกรณี Mean และ Median อาจใกล้กันหรือเท่ากัน ในขณะที่กรณีอื่นๆ อาจแตกต่างกันเนื่องจากการมี Outliers หรือการแจกแจงเฉพาะของข้อมูล

เรียนรู้วิธีคำนวณ Median ด้วยมือ Excel และ R ได้อย่างง่ายดาย

3. Mode: ค่าที่พบบ่อยที่สุด

Mode คือค่าที่เกิดขึ้นบ่อยที่สุดในชุดข้อมูล แสดงถึงการสังเกตที่พบบ่อยที่สุดในข้อมูลของคุณ

ไม่เหมือนกับ Mean ไม่มีสมการทางคณิตศาสตร์เฉพาะเพื่อคำนวณ Mode Mode เป็นเพียงค่าที่เกิดขึ้นบ่อยที่สุดในชุดข้อมูล เพื่อหา Mode คุณต้องนับความถี่ของแต่ละค่าที่ไม่ซ้ำในชุดข้อมูลและระบุค่าที่มีความถี่สูงสุด

ในบางกรณี ชุดข้อมูลอาจมี:

  • Mode เดียว (Unimodal): ค่าเดียวเกิดขึ้นบ่อยกว่าค่าอื่นๆ

  • สอง Mode (Bimodal): สองค่าที่แตกต่างกันเกิดขึ้นด้วยความถี่สูงสุดเท่าๆ กัน

  • หลาย Mode (Multimodal): มากกว่าสองค่าเกิดขึ้นด้วยความถี่สูงสุดเท่าๆ กัน

  • ไม่มี Mode: ค่าทั้งหมดในชุดข้อมูลเกิดขึ้นด้วยความถี่เท่ากัน

สิ่งสำคัญคือต้องทราบว่า Mode สามารถใช้กับข้อมูลทุกประเภท รวมถึงข้อมูลประเภท Nominal, Ordinal, Interval หรือ Ratio เพราะมันอาศัยเพียงความถี่ของแต่ละค่าที่ไม่ซ้ำกัน

Histogram สำหรับ Mode พร้อมเส้นแนวตั้งที่แทนค่า Mode มีลักษณะดังนี้:

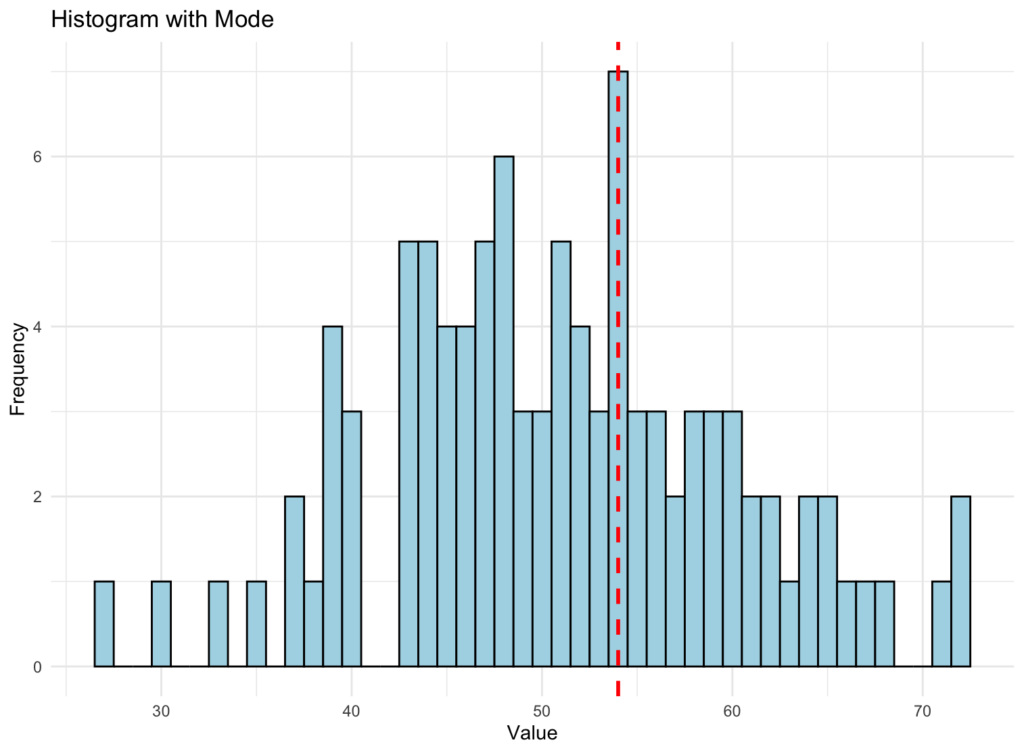
Histogram แสดงค่า Mode ของชุดข้อมูล พร้อมเส้นสีแดงประแสดงตำแหน่งฐานนิยม

Histogram แสดงการแจกแจงข้อมูลพร้อมเส้นประสีแดงที่แสดงตำแหน่งค่า Mode

นี่คือการอธิบายง่ายๆ ว่า Histogram ของ Mode ด้านบนบอกเราอะไร:

  • Histogram คือการแสดงภาพของชุดข้อมูล มันแบ่งข้อมูลออกเป็นช่วงจำนวนหนึ่ง และความสูงของแต่ละแท่งใน Histogram แสดงความถี่ (จำนวนครั้ง) ที่ข้อมูลตกอยู่ในช่วงเฉพาะนั้น กล่าวคือ แท่งที่สูงกว่าบ่งชี้ว่ามีข้อมูลมากกว่าในช่วงค่านั้น

  • เส้นสีแดงประในกราฟแทนค่า Mode ของชุดข้อมูล Mode คือค่าที่เกิดขึ้นบ่อยที่สุดในชุดข้อมูล เป็น Measure of Central Tendency ที่สามารถช่วยระบุค่าที่พบบ่อยที่สุดของชุดข้อมูล

เมื่อดูที่ Histogram ของ Mode คุณสามารถเห็นว่าข้อมูลถูกกระจายอย่างไร และเส้นแนวตั้งช่วยให้คุณระบุว่าค่า Mode อยู่ที่ไหนภายในการแจกแจงนั้น

Mode สามารถให้ข้อมูลเชิงลึกเกี่ยวกับพฤติกรรมทั่วไปของชุดข้อมูลและช่วยให้คุณเข้าใจค่าที่พบบ่อยที่สุด ไม่เหมือนกับ Mean และ Median Mode ไม่ได้รับผลกระทบจาก Outliers หรือค่าสุดขั้ว ทำให้เป็น Measure of Central Tendency ที่เหมาะสมเมื่อชุดข้อมูลมีการแจกแจงที่เบ้หรือมี Outliers

เรียนรู้วิธีคำนวณ Mode ด้วยมือ Excel และ R อย่างรวดเร็ว

ทำไมเราต้องสนใจเกี่ยวกับ Measure of Central Tendency?

Measure of Central Tendency ถูกใช้เพื่อวิเคราะห์และตีความข้อมูลในสาขาต่างๆ เช่น สถิติ เศรษฐศาสตร์ จิตวิทยา และวิทยาศาสตร์อื่นๆ พวกมันช่วยเราให้:

  • สรุปชุดข้อมูลขนาดใหญ่: แทนที่จะวิเคราะห์ข้อมูลทุกจุด เราสามารถใช้ Measure of Central Tendency เพื่อให้ได้ความคิดทั่วไปว่าข้อมูลมีลักษณะอย่างไร สิ่งนี้ทำให้การวิเคราะห์ของเราง่ายขึ้นและทำให้เข้าใจรูปแบบหรือแนวโน้มโดยรวมในข้อมูลได้ง่ายขึ้น

  • เปรียบเทียบชุดข้อมูลที่แตกต่างกัน: Measure of Central Tendency ช่วยให้เราเปรียบเทียบชุดข้อมูลโดยการให้ค่าเดียวที่แทนศูนย์กลางของแต่ละชุดข้อมูล สิ่งนี้ทำให้ง่ายต่อการเห็นว่าชุดข้อมูลใดมีค่าที่สูงกว่าหรือต่ำกว่าโดยเฉลี่ย

  • ระบุแนวโน้มและรูปแบบ: โดยการดูที่ Mean, Median หรือ Mode เราสามารถระบุแนวโน้มและรูปแบบในข้อมูล สิ่งนี้มีประโยชน์สำหรับการคาดการณ์ การระบุพื้นที่สำหรับการปรับปรุง หรือการติดตามการเปลี่ยนแปลงเมื่อเวลาผ่านไป

  • ตัดสินใจอย่างมีข้อมูล: ในหลายสาขา ผู้ตัดสินใจพึ่งพา Measure of Central Tendency เพื่อแนะนำการเลือกของพวกเขา ตัวอย่างเช่น เจ้าของธุรกิจอาจดูที่รายได้เฉลี่ยของผลิตภัณฑ์ต่างๆ เพื่อตัดสินใจว่าจะโฟกัสที่การส่งเสริมการขายอันไหน หรือครูอาจใช้คะแนนทดสอบ Median เพื่อกำหนดประสิทธิผลของวิธีการสอนของพวกเขา

วิธีเลือก Measure of Central Tendency ที่เหมาะสม

ตอนนี้คุณรู้แล้วว่า Measure of Central Tendency คืออะไรและทำไมมันถึงสำคัญ คุณอาจสงสัยว่าควรใช้ตัวไหนในสถานการณ์ต่างๆ นี่คือแนวทางทั่วไปเพื่อช่วยคุณเลือกค่าที่เหมาะสมกับความต้องการของคุณ:

  • ใช้ Mean เมื่อ: ข้อมูลของคุณมีความสมมาตรค่อนข้างมากและไม่มีค่าสุดขั้วหรือ Outliers Mean เหมาะสำหรับการให้แนวโน้มโดยรวมในข้อมูลและถูกใช้กันทั่วไปในหลายสาขา

  • ใช้ Median เมื่อ: ข้อมูลของคุณเบ้หรือมีค่าสุดขั้วที่อาจส่งผลต่อ Mean Median ไม่ไวต่อ Outliers และแทนศูนย์กลางได้ดีกว่าสำหรับการแจกแจงที่เบ้

  • ใช้ Mode เมื่อ: คุณต้องการระบุค่าที่พบบ่อยที่สุดหรือได้รับความนิยมมากที่สุดในชุดข้อมูล Mode มีประโยชน์อย่างยิ่งสำหรับข้อมูลเชิงหมวดหมู่หรือข้อมูลแบบไม่ต่อเนื่องที่ Measure of Central Tendency อื่นๆ อาจไม่เหมาะสม

คำถามที่พบบ่อย

Mean คือค่าเฉลี่ยเลขคณิตที่คำนวณโดยการรวมค่าทั้งหมดและหารด้วยจำนวน Median คือค่ากลางเมื่อข้อมูลถูกเรียงลำดับจากน้อยไปมาก Mode คือค่าที่ปรากฏบ่อยที่สุดในชุดข้อมูล แต่ละมาตรการมีจุดประสงค์ที่แตกต่างกัน: Mean เหมาะที่สุดสำหรับข้อมูลที่กระจายตัวแบบปกติโดยไม่มี Outliers, Median ใช้งานได้ดีกับข้อมูลที่เบ้หรือมี Outliers และ Mode เหมาะสำหรับข้อมูลเชิงหมวดหมู่หรือการหาค่าที่พบบ่อยที่สุด
ใช้ Median แทน Mean เมื่อข้อมูลของคุณมี Outliers หรือเบ้ (ไม่กระจายตัวแบบปกติ) Median ต้านทานค่าสุดขั้วเพราะมันพิจารณาเฉพาะตำแหน่งกลางเท่านั้น ไม่ใช่ค่าจริง ตัวอย่างเช่น ในข้อมูลรายได้ที่ผู้มีรายได้สูงมากเพียงไม่กี่คนสามารถทำให้ Mean สูงขึ้น Median จะให้มาตรการที่เป็นตัวแทนของรายได้ทั่วไปมากกว่า Median ยังเป็นที่ต้องการเมื่อทำงานกับข้อมูล Ordinal หรือเมื่อค่าสุดขั้วไม่แทน Central Tendency อย่างแม่นยำ
ได้ ชุดข้อมูลสามารถมีหลาย Modes ได้ เมื่อชุดข้อมูลมีสอง Modes เรียกว่า Bimodal สาม Modes เรียกว่า Trimodal และมากกว่าสามเรียกว่า Multimodal ตัวอย่างเช่น ในชุดข้อมูลคะแนนสอบ (65, 70, 70, 80, 85, 85, 90) ทั้ง 70 และ 85 เป็น Modes เพราะปรากฏสองครั้ง ชุดข้อมูลที่ไม่มีค่าซ้ำไม่มี Mode หลาย Modes สามารถบ่งบอกถึงกลุ่มย่อยที่แตกต่างกันในข้อมูลของคุณหรือหลายยอดในการกระจาย
Outliers ส่งผลกระทบอย่างมากต่อ Mean เพราะใช้ค่าทั้งหมดในการคำนวณ - ค่าสุดขั้วเพียงค่าเดียวสามารถดึง Mean ออกจากศูนย์กลางทั่วไป Median ต้านทาน Outliers เพราะพิจารณาเฉพาะตำแหน่งกลาง ไม่ใช่ค่าสุดขั้วจริง Mode ไม่ได้รับผลกระทบจาก Outliers เลยเว้นแต่ Outlier เองเป็นค่าที่พบบ่อยที่สุด ตัวอย่างเช่น ในชุดข้อมูล (10, 12, 13, 14, 100) Mean คือ 29.8 (ได้รับอิทธิพลอย่างมากจาก 100) แต่ Median ยังคงเป็น 13 (เป็นตัวแทนของค่าทั่วไป)
เมื่อ Mean, Median และ Mode เท่ากัน (หรือใกล้เคียงกันมาก) บอกว่ามีการกระจายแบบสมมาตร ปกติ ไม่มีความเบ้ นี่คือเส้นโค้งรูประฆังคลาสสิกที่ข้อมูลกระจายอย่างสม่ำเสมอรอบศูนย์กลาง ในการกระจายดังกล่าว ทั้งสามมาตรการชี้ไปที่ค่ากลางเดียวกัน ทำให้มาตรการใดๆ เป็น Measure of Central Tendency ที่เชื่อถือได้ นี่เป็นเรื่องปกติในปรากฏการณ์ที่เกิดขึ้นตามธรรมชาติเช่นความสูงของมนุษย์ คะแนนสอบในประชากรขนาดใหญ่ หรือข้อผิดพลาดการวัด
เมื่อคุณมีจำนวนค่าคู่ Median คือค่าเฉลี่ยของสองค่ากลาง ขั้นแรก เรียงข้อมูลของคุณตามลำดับจากน้อยไปมาก จากนั้นระบุสองตัวเลขกลางและคำนวณค่าเฉลี่ยของพวกมัน ตัวอย่างเช่น ในชุดข้อมูล (3, 5, 7, 9) สองค่ากลางคือ 5 และ 7 Median คือ (5 + 7) / 2 = 6 ด้วยจำนวนค่าคี่ Median เป็นเพียงค่ากลางหลังจากเรียงข้อมูล
Mode เป็น Measure of Central Tendency เดียวที่เหมาะสมสำหรับข้อมูลเชิงหมวดหมู่ (Nominal) เพราะคุณไม่สามารถคำนวณค่าเฉลี่ยหรือค่ากลางที่มีความหมายสำหรับหมวดหมู่เช่นสี ชื่อ หรือประเภท ตัวอย่างเช่น ถ้าคุณสำรวจสีโปรดและได้ (แดง, น้ำเงิน, น้ำเงิน, เขียว, น้ำเงิน, แดง, น้ำเงิน) Mode คือน้ำเงิน (ปรากฏ 4 ครั้ง) คุณไม่สามารถคำนวณ Mean หรือ Median สำหรับหมวดหมู่สีเพราะไม่มีค่าตัวเลขหรือลำดับตามธรรมชาติ สำหรับข้อมูล Ordinal (หมวดหมู่ที่เรียงลำดับเช่นการจัดอันดับ) คุณสามารถใช้ Mode หรือ Median แต่ไม่ใช่ Mean
Weighted Mean กำหนดระดับความสำคัญที่แตกต่างกัน (น้ำหนัก) ให้กับค่าต่างๆ ในชุดข้อมูลของคุณ แทนที่จะปฏิบัติกับค่าทั้งหมดเท่าเทียมกัน คำนวณโดยการคูณแต่ละค่าด้วยน้ำหนักของมัน รวมผลคูณเหล่านี้ และหารด้วยผลรวมของน้ำหนัก สูตรคือ: Weighted Mean = Σ(ค่า × น้ำหนัก) / Σ(น้ำหนัก) ใช้ Weighted Means เมื่อบางการสังเกตสำคัญกว่าอื่นๆ เช่นการคำนวณเกรดเฉลี่ย (ที่วิชาต่างๆ มีชั่วโมงเครดิตต่างกัน) ดัชนีทางการเงิน (ที่บริษัทมี Market Capitalization ต่างกัน) หรือข้อมูลการสำรวจ (ที่คำตอบถูกถ่วงน้ำหนักเพื่อให้ตรงกับข้อมูลประชากร)

สรุป

Measure of Central Tendency (Mean, Median และ Mode) เป็นเครื่องมือสำคัญสำหรับการสรุปและทำความเข้าใจการกระจายของข้อมูล แต่ละมาตรการมีข้อได้เปรียบที่เป็นเอกลักษณ์ Mean ให้ค่าเฉลี่ยโดยรวม Median ต้านทานอิทธิพลของค่าผิดปกติ และ Mode ระบุค่าที่พบบ่อยที่สุดในชุดข้อมูลของคุณ

โดยการเลือก Measure of Central Tendency ที่เหมาะสมสำหรับลักษณะข้อมูลเฉพาะและคำถามการวิจัยของคุณ คุณสามารถสรุปข้อสรุปที่แม่นยำยิ่งขึ้นและตัดสินใจที่มีข้อมูลดีขึ้นจากการวิเคราะห์ทางสถิติของคุณ