Media, modul și mediana sunt trei măsuri fundamentale de tendință centrală în statistică care te ajută să înțelegi valoarea tipică sau centrală într-un set de date. Fie că analizezi scoruri de test, cifre de vânzări sau răspunsuri la sondaje, aceste statistici oferă perspective diferite asupra a ceea ce este "normal" sau "mediu" în datele tale.
În acest ghid, vei învăța cum să calculezi media, modul și mediana manual folosind formule simple, apoi vei descoperi metode mai rapide folosind funcțiile Excel și programarea R. Fiecare măsură are puncte forte unice și, la sfârșitul acestui tutorial, vei ști când să folosești fiecare dintre ele.
Cum Să Calculezi Media în Statistică
Media (media aritmetică) se calculează adunând toate valorile dintr-un set de date și împărțind la numărul total de valori. Este cea mai frecvent folosită măsură a tendinței centrale.
Formula:
Unde Σx este suma tuturor valorilor și n este numărul de valori.
Exemplu:
Imaginează-ți că ești profesor și calculezi scorul mediu al testului pentru clasa ta. Scorurile sunt:
Pasul 1: Adună toate scorurile împreună:
Pasul 2: Împarte la numărul de scoruri (7):
Scorul mediu al testului este 82.7 puncte.
Calculează Media în Excel
Funcția AVERAGE din Excel face calcularea mediei rapidă și ușoară:
- Fă clic pe o celulă goală unde dorești rezultatul
- Tastează
=AVERAGE(în celulă - Selectează intervalul de celule care conțin datele tale (de ex.,
A1:A10) - Închide parantezele și apasă Enter
Exemplu:
=AVERAGE(A1:A10)
Calculează Media în R
R oferă o funcție încorporată mean() pentru calcule rapide:
# Creează un vector cu date exemplu
data <- c(10, 20, 30, 40, 50)
# Calculează media
mean_value <- mean(data)
# Afișează rezultatul
print(mean_value)
# Ieșire: 30Media este 30 (suma 150 împărțită la 5 valori).
Cum Să Calculezi Modul în Statistică
Modul este valoarea care apare cel mai frecvent într-un set de date. Spre deosebire de medie și mediană, un set de date poate avea:
- Un singur mod (unimodal)
- Mai multe moduri (bimodal sau multimodal)
- Fără mod (toate valorile apar cu frecvență egală)
Exemplu:
Presupune că deții un magazin de încălțăminte și vrei să găsești mărimea de pantof cea mai comună. Ultimii tăi 20 de clienți au cumpărat aceste mărimi:
Numără frecvența:
| Mărimea Pantofului | Frecvență |
|---|---|
| 7 | 5 ori |
| 8 | 5 ori |
| 9 | 6 ori |
| 10 | 4 ori |
| 11 | 1 dată |
Modul este mărimea 9 (apărând de 6 ori, mai mult decât orice altă mărime).
Calculează Modul în Excel
Excel oferă două funcții de mod:
Mod Singular (Date Unimodale)
Folosește MODE.SNGL pentru seturi de date cu o singură valoare cea mai frecventă:
=MODE.SNGL(A1:A10)
Moduri Multiple (Date Multimodale)
Folosește MODE.MULT pentru seturi de date cu mai multe valori cele mai frecvente:
=MODE.MULT(A1:A10)
Pentru a afișa toate modurile, introdu formula și apasă Ctrl+Shift+Enter (formulă array), apoi copiază în celulele adiacente.
Calculează Modul în R
R nu are o funcție încorporată de mod, dar poți să-l calculezi ușor:
# Creează un vector
shoe_sizes <- c(7, 8, 9, 7, 10, 9, 8, 7, 11, 10, 9, 7, 9, 8, 8, 10, 7, 9, 8, 10)
# Calculează modul
mode_value <- as.numeric(names(which.max(table(shoe_sizes))))
# Afișează rezultatul
print(mode_value)
# Ieșire: 9Cum Să Calculezi Mediana în Statistică
Mediana este valoarea din mijloc când toate valorile sunt aranjate în ordine crescătoare sau descrescătoare. Împarte setul de date în jumătate—50% din valori sunt sub mediană și 50% sunt deasupra ei.
Mediana este mai robustă la valori aberante decât media, ceea ce o face utilă pentru date asimetrice.
Formula:
- Număr impar de valori: Mediana este valoarea din mijloc
- Număr par de valori: Mediana este media celor două valori din mijloc
Exemplu:
Analizezi veniturile gospodăriilor (în mii de dolari) într-o vecinătate:
Pasul 1: Aranjează în ordine crescătoare:
Pasul 2: Găsește valoarea din mijloc (poziția a 5-a din 9 valori):
Mediana este 65 (valoarea exactă din mijloc cu 4 valori sub și 4 valori deasupra).
Calculează Mediana în Excel
Folosește funcția MEDIAN din Excel:
- Fă clic pe o celulă goală
- Tastează
=MEDIAN( - Selectează intervalul de date (de ex.,
A1:A10) - Închide parantezele și apasă Enter
Exemplu:
=MEDIAN(A1:A10)
Calculează Mediana în R
Funcția încorporată median() din R calculează mediana:
# Creează un vector
data <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
# Calculează mediana
data_median <- median(data)
# Afișează rezultatul
print(data_median)
# Ieșire: 5.5Cu 10 valori (număr par), mediana este media valorilor a 5-a (5) și a 6-a (6):
Vizualizarea Mediei, Modului și Medianei în R
Iată codul R pentru a vizualiza toate cele trei măsuri pe o histogramă folosind exemplul mărimilor de pantofi:
# Încarcă biblioteca necesară
library(ggplot2)
# Set de date
shoe_sizes <- c(7, 8, 9, 7, 10, 9, 8, 7, 11, 10, 9, 7, 9, 8, 8, 10, 7, 9, 8, 10)
# Calculează media, modul și mediana
mean_size <- mean(shoe_sizes)
mode_size <- as.numeric(names(which.max(table(shoe_sizes))))
median_size <- median(shoe_sizes)
# Creează histogramă cu linii verticale
hist_plot <- ggplot(data.frame(shoe_sizes), aes(shoe_sizes)) +
geom_histogram(binwidth = 1, fill = "lightblue", color = "black") +
geom_vline(aes(xintercept = mean_size), color = "blue",
linetype = "dashed", size = 1.5) +
geom_vline(aes(xintercept = mode_size), color = "red",
linetype = "dashed", size = 1.5) +
geom_vline(aes(xintercept = median_size), color = "green",
linetype = "dashed", size = 1.5) +
labs(title = "Distribuția Mărimilor de Pantofi",
subtitle = "Media (albastru), Modul (roșu), Mediana (verde)",
x = "Mărimea Pantofului",
y = "Frecvență") +
theme_minimal()
# Afișează graficul
print(hist_plot)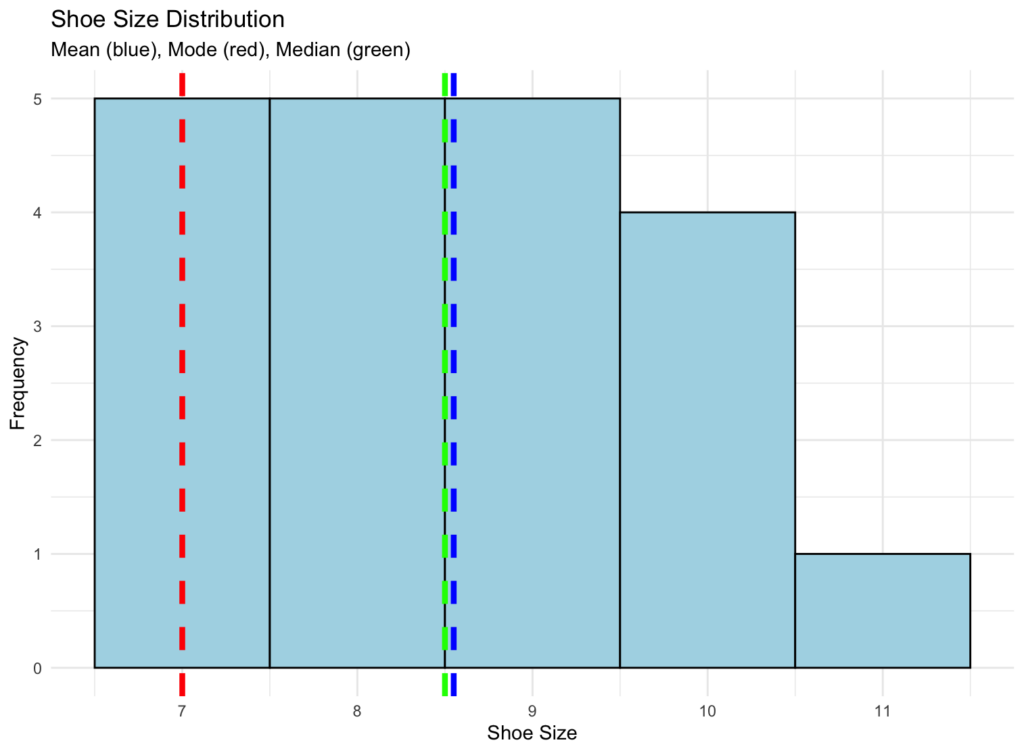
Această vizualizare te ajută să vezi cum se raportează aceste trei măsuri la distribuția datelor tale. Modul apare la vârf (valoarea cea mai frecventă), în timp ce media și mediana arată aspecte diferite ale centrului datelor.
Relația Dintre Media, Mediana și Mod
Relația dintre media, mediana și mod dezvăluie informații importante despre distribuția și asimetria datelor tale.
În Distribuții Simetrice (Normale)
Când datele sunt perfect simetrice și distribuite normal (curbă în formă de clopot):
Toate cele trei măsuri converg în centrul distribuției. Acesta este scenariul ideal pentru majoritatea analizelor statistice.
Exemplu: Înălțimile bărbaților adulți urmează adesea o distribuție normală unde înălțimea medie (media), înălțimea din mijloc (mediana) și înălțimea cea mai comună (modul) sunt toate aproximativ aceleași.
În Distribuții Asimetrice Dreapta (Pozitiv Asimetrice)
Când datele au o coadă lungă spre dreapta (frecvent cu venituri, prețuri case):
Media este trasă spre coadă de valorile extreme ridicate, în timp ce mediana rămâne în mijloc, iar modul rămâne la vârf.
Exemplu: Distribuția veniturilor gospodăriilor
- Mod: $45,000 (venitul cel mai comun)
- Mediană: $65,000 (valoarea din mijloc)
- Medie: $85,000 (trasă în sus de cei cu venituri mari)
În Distribuții Asimetrice Stânga (Negativ Asimetrice)
Când datele au o coadă lungă spre stânga:
Media este trasă spre coadă de valorile extreme joase.
Exemplu: Scoruri de test unde majoritatea studenților obțin scoruri mari (90+) dar câțiva obțin scoruri foarte joase.
Formula Relației Empirice
Pentru distribuții moderat asimetrice, există o relație aproximativă:
Această relație empirică te poate ajuta să estimezi o măsură când cunoști celelalte două, deși este cea mai precisă pentru distribuții unimodale, moderat asimetrice.
Când Să Folosești Media, Modul sau Mediana
Fiecare măsură a tendinței centrale are cazuri specifice de utilizare:
Folosește Media când:
- Datele sunt distribuite normal (simetrice, în formă de clopot)
- Trebuie să iei în considerare toate valorile din setul de date
- Efectuezi calcule statistice suplimentare (abatere standard, varianță)
Folosește Mediana când:
- Datele au valori aberante sau extreme
- Datele sunt asimetrice (nu distribuite normal)
- Analizezi venituri, prețuri de locuințe sau alte date asimetrice dreapta
- Dorești o măsură rezistentă la valori extreme
Folosește Modul când:
- Analizezi date categoriale (culori, mărimi, categorii)
- Găsești valoarea cea mai comună sau populară
- Datele au mai multe vârfuri (distribuții bimodale sau multimodale)
- Lucrezi cu date discrete (mărimi de pantofi, număr de copii)
Întrebări Frecvente
Concluzie
Calcularea mediei, modului și medianei este fundamentală pentru înțelegerea datelor tale. Fiecare măsură oferă perspective unice asupra tendinței centrale, iar cunoașterea când să folosești fiecare dintre ele este crucială pentru analiza precisă a datelor.
Fie că calculezi aceste măsuri manual pentru seturi de date mici, folosești funcțiile Excel pentru analiză rapidă sau valorifici R pentru lucrări statistice complexe, aceste instrumente formează fundamentul statisticilor descriptive. Practicarea cu diferite seturi de date te va ajuta să dezvolți intuiția despre care măsură reprezintă cel mai bine tendința centrală a datelor tale.