What's the difference between moderator and mediator variables? Here's the simple answer: mediators explain HOW or WHY an effect occurs, while moderators explain WHEN or FOR WHOM an effect occurs.
Though mediator and moderator variables both play important roles in understanding relationships between variables, they serve fundamentally different purposes in research. A mediator acts as a "middleman" that transmits the effect from independent to dependent variable, while a moderator changes the strength or direction of that relationship.
Understanding this distinction is critical for designing research studies and correctly interpreting results. Let's dive into the key differences between these two types of variables and how they function in statistical analysis.
Mediators vs. Moderators: Key Differences
From a deterministic point of view, the main differences between mediators vs. moderators are as follows:
- A mediator is the reason for the effect and acts like a "middleman" in the relationship between independent and dependent variables. If the mediator variable is removed, the causal link between independent and dependent variables disappears.
- A mediator variable MUST be a causal result of the independent variable and a causal precursor of the dependent variable. In other words, a mediator explains the mechanism of the effect.
- A moderator variable changes the effect (level of strength, direction) between the independent and dependent variables.
- A moderator variable MUST NOT be the causal effect of the independent variable.
I don't blame you if you have trouble seeing the difference. Let's take one step at a time and understand the purpose of each variable as well as look to some examples of mediators vs. moderators to make sure the matter is settled once for all.
Moderator vs Mediator: Quick Comparison Table
To help you quickly distinguish between these two types of variables, here's a comprehensive comparison:
| Characteristic | Mediator Variable | Moderator Variable |
|---|---|---|
| Answers the question | HOW or WHY does X affect Y? | WHEN or FOR WHOM does X affect Y? |
| Function | Explains the mechanism/pathway of the effect | Changes the strength or direction of the effect |
| Relationship to X | MUST be caused by X | MUST NOT be caused by X |
| Relationship to Y | MUST cause Y | Affects the X→Y relationship strength |
| Position in model | Located between X and Y (X → Me → Y) | Interacts with X to influence Y (X × Mo → Y) |
| Effect if removed | The X→Y relationship disappears or weakens | The X→Y relationship remains but may vary by group |
| Correlation with X & Y | MUST correlate with both X and Y | Does NOT need to correlate with X or Y |
| Statistical test | Mediation analysis (Baron & Kenny, bootstrapping) | Moderation analysis (interaction term in regression) |
| Path model | Indirect effect through mediator | Interaction effect with moderator |
| Example | Exercise → Endorphins → Mood | Social support × Personality type → Stress reduction |
This table provides a quick reference, but let's dive deeper into each concept.
Learning Outcomes
In this article, we are going to shed some light on the main difference between mediators vs. moderators. Here are the key learning outcomes you should expect to attain:
- What is a mediator variable?
- What is a moderator variable?
- Key differences between mediators vs. moderators variables
- Statistical methods for testing mediation and moderation
- 10+ practical examples from real research
- Learn to spot a mediator vs. moderator variable in a study
Without further ado, let's hit the road!
What is a Mediating Variable? [Definition + How It Works]
Definition: A mediating variable (or mediator) explains the "why" and "how" behind the relationship between the independent variable (X) and the dependent variable (Y). In other words, mediation reveals the mechanism or pathway through which an effect occurs.
In mediation analysis, the independent variable does not infer directly the dependent variable but rather through a third variable mediator or "middleman" between the two. In other words, if we remove the mediator variable, the causal effect between X and Y variables will cease to exist.
A mediated model consists of two paths: the direct effect path (c or c') from X to Y, and the indirect effect path (a and b) from X → Me → Y, as seen in the following figure.
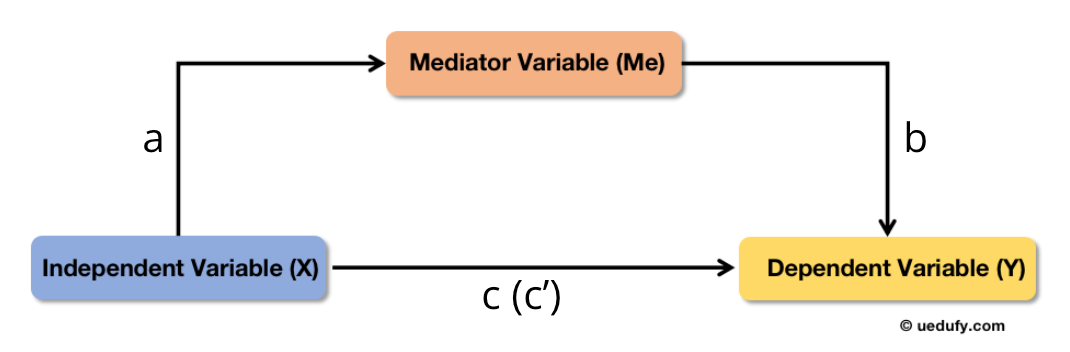 Mediation model showing paths a, b, and c (c'). Adaptation from Baron and Kenny (1986).
Mediation model showing paths a, b, and c (c'). Adaptation from Baron and Kenny (1986).
When we talk about mediation, your research model must meet the following conditions:
- The X and Y variables (path c) must be significantly correlated before testing mediator effects.
- X, Me, and Y (paths a and b) must show significant correlations.
- When a mediation variable is added, the strength between X and Y (path c) should decrease partially or completely (becoming c').
- Variables in mediation analysis are expected to share variance, as both X and Me explain the dependent variable Y.
Note: Correlations can be positive or negative depending on your theoretical model. The key is that they must be statistically significant.
It is important to note that correlation does not imply causality between variables, but correlation is a necessary (though not sufficient) condition for establishing causal relationships in regression analysis.
Based on the above conditions we can say that the effect of a mediator variable on the relationship between independent and dependent variables can be partial or complete.
-
Partial mediation happens when the mediator partially explains the relationship between X and Y. The direct effect (path c') diminishes but remains significant.
-
Complete mediation happens when the direct effect (path c') becomes non-significant, meaning the entire X→Y relationship is explained by the indirect path through the mediator (paths a and b).
How to Test for Mediation: Statistical Methods
Testing for mediation requires specific statistical procedures to determine whether a variable truly acts as a mediator. Here are the main approaches:
1. Baron & Kenny's 4-Step Approach (1986)
The classic Baron & Kenny method involves four regression steps:
Step 1: Test if X significantly predicts Y (the total effect, path c)
- Regression:
- Result: must be significant (p < 0.05)
Step 2: Test if X significantly predicts Me (path a)
- Regression:
- Result: must be significant (p < 0.05)
Step 3: Test if Me significantly predicts Y when controlling for X (path b)
- Regression:
- Result: must be significant (p < 0.05)
Step 4: Compare the direct effect (path c') to the total effect (path c)
- Partial mediation: If c' is smaller than c but still significant
- Complete mediation: If c' becomes non-significant when Me is added
Important note: While historically popular, Baron & Kenny's approach has limitations. Modern researchers recommend bootstrapping methods instead (Hayes, 2009).
2. Sobel Test
The Sobel test examines whether the indirect effect (a × b) is significantly different from zero:
Formula:
Where:
- = coefficient of X → Me
- = coefficient of Me → Y (controlling for X)
- and = standard errors
Limitation: The Sobel test assumes normal distribution of the indirect effect, which is often violated in small samples. Bootstrapping is now preferred.
3. Bootstrapping Method (Hayes, 2009) - Recommended
Bootstrapping is the gold standard for testing mediation because it:
- Makes no assumptions about the distribution of the indirect effect
- Provides more accurate confidence intervals
- Has greater statistical power than Sobel test
How it works:
- Resample your data with replacement thousands of times (e.g., 5,000 iterations)
- Calculate the indirect effect (a × b) for each resampled dataset
- Create a 95% confidence interval from the distribution of indirect effects
- If the CI does not include zero, mediation is significant
Interpretation:
- If 95% CI excludes zero → Significant mediation effect
- Example: CI [0.12, 0.54] indicates significant mediation
4. PROCESS Macro for SPSS, SAS, and R
The easiest way to conduct mediation analysis is using the PROCESS macro developed by Andrew Hayes. See our step-by-step SPSS installation guide to get started.
Advantages:
- Automatically performs bootstrapping (recommended: 5,000 samples)
- Provides bias-corrected confidence intervals
- Tests direct and indirect effects
- Available for SPSS, SAS, and R
- Free to download
PROCESS Syntax (SPSS):
PROCESS y=DV/x=IV/m=Mediator/model=4/boot=5000/conf=95.
Output interpretation:
- Total effect (c): Overall effect of X on Y
- Direct effect (c'): Effect of X on Y controlling for mediator
- Indirect effect (a×b): Effect transmitted through mediator
- Bootstrap CI: If CI excludes zero, mediation is significant
For a detailed tutorial on mediation analysis, see our guide on how to run mediation analysis in SPSS.
Next, let's have a look at what moderation is and when it should be used in statistical research.
What is a Moderating Variable? [Definition + How It Works]
Definition: A moderating variable (or moderator) is a third variable that affects the strength or direction of the relationship between the independent (X) and dependent (Y) variables. Moderation is quantified by the linear regression coefficient of the interaction term.
In simple terms, moderators answer the question "WHEN" or "FOR WHOM" does the relationship between X and Y hold true.
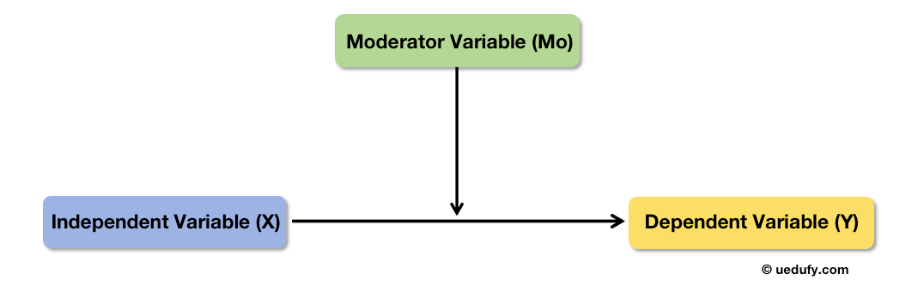 Moderation model showing how moderator Mo influences the X→Y relationship strength. Adaptation from Baron and Kenny (1986).
Moderation model showing how moderator Mo influences the X→Y relationship strength. Adaptation from Baron and Kenny (1986).
In regression, the interaction term (also known as product term) refers to the effect observed in a dependent variable based on how a third variable (Mo) affects the relationship between X and Y.
The diagram shows how the moderator (Mo) influences the X→Y relationship. A moderation variable can affect the strength of this relationship, and less commonly, change the direction of the effect (Whisman & McClelland, 2005).
Because the moderation effect basically tests the residual variance in a model, it is important to investigate what are the main effects between X and Y variables before testing if the interaction term is significant (p-value < 0.05).
In order to do so, we must check the beta (β) coefficient which indicates how much the relationship between X and Y varies as a function of a one-unit change in the Mo variable.
It is important to keep in mind that statistically, it is challenging to detect moderation effects. One reason is that you may fail to detect an effect that actually happens (Type 2 Error).
One way to avoid this issue is by doing purposive sampling instead of convenience sampling. In other words, your sample needs to contain jointly extreme cases, namely cases that are extreme in both levels. What does that mean?
Take a look at the following diagram showing how the moderator variable (Mo) changes the strength of the X→Y relationship. The graph displays three moderator levels (Low, Medium, High), demonstrating that as the moderator increases, the slope of the relationship becomes steeper. For moderation analysis, we need to collect data that represents variation across moderator levels, with normally distributed values.
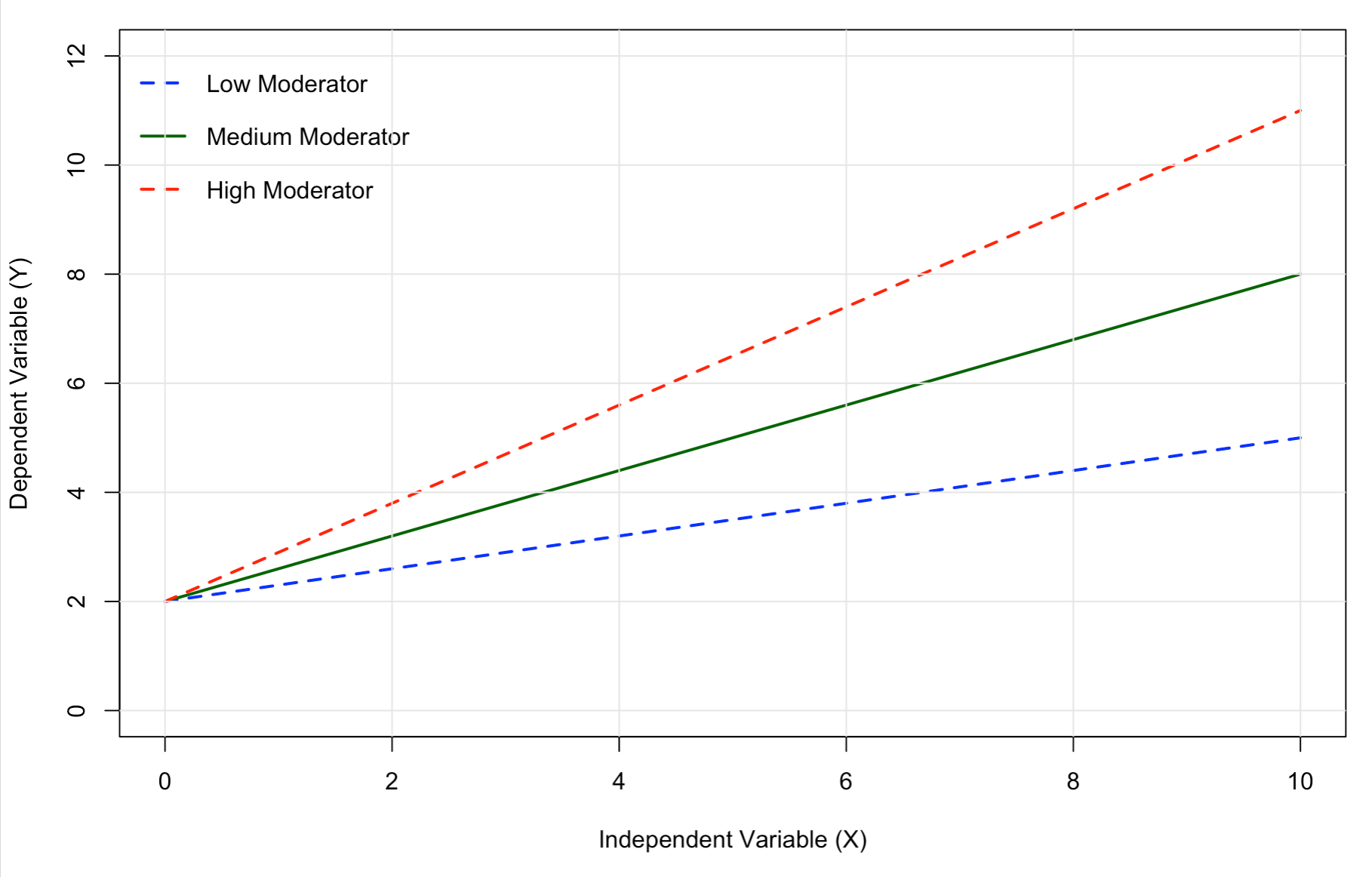 Moderation effect: The graph shows how the relationship between X and Y strengthens as the moderator increases from low to high levels.
Moderation effect: The graph shows how the relationship between X and Y strengthens as the moderator increases from low to high levels.
This can be quite challenging if we choose convenience sampling (using no selection pattern when sampling a population) for a study unless the sample size is large enough to fit the model.
A better approach would be purposive sampling where we can choose members of a population, based on specific selection criteria (e.g., age, gender, etc.).
For example, choosing purposive sampling when investigating the effect of age on the relationship between reading and information retention, allows us to select members of different age groups representing the various levels of strengths (e.g., age between 20-30, 31-40, etc.). This would be very difficult using convenience sampling where respondents are selected based on convenience rather than specific selection criteria.
How to Test for Moderation: Statistical Methods
Testing for moderation involves examining whether the relationship between X and Y changes as a function of a third variable (the moderator). Here's how to do it:
1. Hierarchical Multiple Regression
The standard approach to testing moderation uses hierarchical regression with an interaction term:
Step 1: Center your variables (recommended)
- Create mean-centered versions of X and Mo
- equals
- equals
- Why? Reduces multicollinearity and aids interpretation
Step 2: Create the interaction term
- equals
Step 3: Run hierarchical regression
Model 1 (Main effects only):
Model 2 (Add interaction):
Interpretation:
- If is significant (p < 0.05), moderation exists
- The change from Model 1 to Model 2 indicates the variance explained by moderation
- The β coefficient of the interaction term shows the moderation effect size
2. Simple Slopes Analysis
After finding a significant interaction, perform simple slopes analysis to understand the nature of the moderation:
What it does: Examines the relationship between X and Y at different levels of the moderator:
- Low Mo (typically Mean - 1 SD)
- Medium Mo (Mean)
- High Mo (Mean + 1 SD)
Example interpretation:
- At low social support (Mo), stress (X) strongly predicts depression (Y): β = 0.65, p < 0.001
- At high social support (Mo), stress weakly predicts depression: β = 0.22, p = 0.08
- Conclusion: Social support moderates the stress-depression relationship
3. Visualizing Moderation Effects
Always plot the interaction to aid interpretation:
- X-axis: Independent variable
- Y-axis: Dependent variable
- Lines: Different levels of moderator (Low, Medium, High)
Interaction patterns:
- Enhancing: Slopes get steeper as Mo increases
- Buffering: Slopes get flatter as Mo increases
- Cross-over: Lines cross, indicating direction reversal
4. PROCESS Macro for Moderation
Just like mediation, the PROCESS macro simplifies moderation analysis. For a complete step-by-step tutorial, see our guide on how to perform moderation analysis in SPSS using PROCESS.
PROCESS Syntax (SPSS):
PROCESS y=DV/x=IV/w=Moderator/model=1/plot=1.
Advantages:
- Automatically centers variables
- Computes interaction term
- Performs simple slopes analysis
- Generates interaction plots
- Provides Johnson-Neyman regions of significance
Output includes:
- Interaction effect: Tests if X × Mo is significant
- Conditional effects: Effect of X on Y at low, medium, high Mo
- Visualization: Interaction plot
5. Categorical Moderators
When the moderator is categorical (e.g., gender, treatment group):
Approach 1: Multiple Group Analysis
- Split sample by moderator groups
- Run separate regressions for each group
- Compare regression coefficients
Approach 2: Dummy Coding
- Create dummy variables for categories
- Test interaction with dummy variables
Example:
Where Gender is coded 0 for Male, 1 for Female
If is significant, the X→Y relationship differs between males and females.
Important Considerations
Statistical Power: Moderation effects are notoriously difficult to detect. You may need:
- Larger sample sizes (n > 200 recommended)
- Purposive sampling to ensure variation in the moderator
- Reliable measures to reduce measurement error
Effect Sizes: Even significant moderation effects tend to be small:
- is considered small
- is considered medium
- is considered large
Moderator vs Mediator Examples [Real Research Cases]
So far we only covered mediators vs. moderators variables from a theoretical point of view. Let's look at practical examples from real research to help you identify which type of variable you're dealing with in your own studies.
Mediator Examples
Example 1: Sleep → Cognitive Abilities → Job Performance
Research question: Why does sleep improve job performance?
- Independent variable (X): Sleep quality
- Dependent variable (Y): Job performance
- Mediator (Me): Cognitive abilities
Why it's a mediator: Sleep doesn't directly improve job performance. Instead, sleep enhances cognitive abilities (memory, attention, problem-solving), which in turn improve job performance. The pathway is: Sleep → Better cognitive function → Better job performance.
Test: Does sleep affect cognitive abilities? Yes, sleep helps brain functions recover. Therefore, cognitive abilities are a mediator that explains HOW sleep affects performance.
Example 2: Exercise → Endorphins → Mood Improvement
Research question: How does exercise improve mood?
- Independent variable (X): Exercise frequency
- Dependent variable (Y): Mood/emotional well-being
- Mediator (Me): Endorphin levels
Why it's a mediator: Exercise triggers the release of endorphins (the "feel-good" hormones), which then improve mood. If you blocked endorphin production, exercise wouldn't improve mood as much.
Example 3: Education → Income → Health Screening Behavior
Research question: Why do educated people get more health screenings?
- Independent variable (X): Education level
- Dependent variable (Y): Health screening frequency
- Mediator (Me): Income level
Why it's a mediator: Education leads to higher-paying jobs, and higher income provides resources for health screenings. Education → Higher income → More health screenings.
Test: Can education affect income? Yes, higher education typically leads to better-paying jobs. Therefore, income is a mediator.
Example 4: Social Media Use → Fear of Missing Out (FOMO) → Anxiety
Research question: Why does social media increase anxiety?
- Independent variable (X): Social media usage
- Dependent variable (Y): Anxiety levels
- Mediator (Me): FOMO (Fear of Missing Out)
Why it's a mediator: Social media exposure creates FOMO by showing others' highlight reels, and FOMO then triggers anxiety. The mechanism is: Social media → FOMO → Anxiety.
Example 5: Therapy → Cognitive Restructuring → Depression Reduction
Research question: How does cognitive behavioral therapy (CBT) reduce depression?
- Independent variable (X): CBT therapy sessions
- Dependent variable (Y): Depression symptoms
- Mediator (Me): Cognitive restructuring (changing negative thought patterns)
Why it's a mediator: CBT works by teaching patients to restructure negative thoughts, and this cognitive change reduces depression. CBT → Changed thinking patterns → Less depression.
Moderator Examples
Example 6: Fitness Training × Age → Muscle Gain
Research question: Does the effect of fitness training on muscle gain depend on age?
- Independent variable (X): Fitness training intensity
- Dependent variable (Y): Muscle gain
- Moderator (Mo): Age
Why it's a moderator: Fitness training works differently for different age groups. Young people (20s) gain muscle more easily than older adults (60s+) with the same training regimen. Age doesn't explain HOW fitness builds muscle; it changes the STRENGTH of the relationship.
Test: Can fitness affect your age? No, you can't change your age through exercise. Therefore, age is a moderator that affects FOR WHOM fitness is most effective.
Example 7: Stress × Social Support → Mental Health
Research question: Does social support change how stress affects mental health?
- Independent variable (X): Stress levels
- Dependent variable (Y): Mental health outcomes
- Moderator (Mo): Social support
Why it's a moderator: For people with high social support, stress has less impact on mental health (buffering effect). For those with low social support, the same stress causes more severe mental health problems. Social support changes WHEN/FOR WHOM stress is harmful.
Example 8: Gender Diversity × Ownership Structure → Corporate Disclosure
Research question: Does the impact of gender diversity on corporate transparency depend on ownership structure?
- Independent variable (X): Gender diversity on board
- Dependent variable (Y): Corporate disclosure quality
- Moderator (Mo): Ownership structure (family vs. public)
Why it's a moderator: Gender diversity may improve disclosure more in publicly-owned companies than family-owned ones. Ownership structure changes the strength of the diversity-disclosure relationship.
Test: Can gender diversity affect ownership structure? No, having more women on the board doesn't change who owns the company. Therefore, ownership structure is a moderator.
Example 9: Study Time × Intelligence → Exam Performance
Research question: Does the benefit of studying depend on student intelligence?
- Independent variable (X): Study time
- Dependent variable (Y): Exam scores
- Moderator (Mo): Intelligence level (IQ)
Why it's a moderator: Students with higher IQ may benefit more from each hour of studying than students with lower IQ. Intelligence changes FOR WHOM studying is most effective, but it doesn't explain HOW studying improves performance.
Example 10: Medication Dosage × Body Weight → Treatment Response
Research question: Does the effect of medication depend on patient body weight?
- Independent variable (X): Medication dosage
- Dependent variable (Y): Treatment effectiveness
- Moderator (Mo): Body weight
Why it's a moderator: The same dosage may be highly effective for a 120-lb patient but insufficient for a 220-lb patient. Body weight moderates WHEN/FOR WHOM a particular dosage works.
Test: Can medication dosage change your body weight? Not directly in this model. Body weight is a moderator affecting the dose-response relationship.
Example 11: Training Program × Prior Experience → Skill Acquisition
Research question: Does the effectiveness of training depend on prior experience?
- Independent variable (X): Training program participation
- Dependent variable (Y): New skill acquisition
- Moderator (Mo): Prior experience level
Why it's a moderator: Beginners and experts learn differently from the same training. Advanced learners may benefit more from challenging programs, while beginners need foundational training. Prior experience moderates FOR WHOM each training approach works best.
Quick Decision Rule
To determine if a variable is a mediator or moderator, ask:
-
Can X cause this variable?
- YES → Potential mediator
- NO → Potential moderator
-
Does this variable explain HOW/WHY X affects Y?
- YES → Mediator
- NO → Check next question
-
Does this variable change WHEN/FOR WHOM X affects Y?
- YES → Moderator
Frequently Asked Questions
Wrapping Up
In conclusion, understanding the distinction between mediators and moderators is fundamental to conducting rigorous research and building strong theoretical models.
Key takeaways:
-
Mediators explain HOW or WHY an effect occurs (the mechanism)
- Must be caused by X and must cause Y
- Tested via indirect effects and bootstrapping
-
Moderators explain WHEN or FOR WHOM an effect occurs (the conditions)
- Cannot be caused by X
- Tested via interaction terms in regression
-
Both types of variables provide valuable insights but serve different theoretical purposes
-
Use the comparison table and decision rules in this article when in doubt
-
Modern analysis uses PROCESS macro with bootstrapping for mediation and hierarchical regression for moderation
When we do research, we are building theory. Correctly identifying and testing mediators and moderators helps us understand not just that relationships exist, but how, why, when, and for whom they occur.
References
Baron, R. M., & Kenny, D. A. (1986). The moderator-mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology, 51(6), 1173–1182. https://doi.org/10.1037/0022-3514.51.6.1173
Hayes, A. F. (2009). Beyond Baron and Kenny: Statistical mediation analysis in the new millennium. Communication Monographs, 76(4), 408–420. https://doi.org/10.1080/03637750903310360
Whisman, M. A., & McClelland, G. H. (2005). Designing, Testing, and Interpreting Interactions and Moderator Effects in Family Research. Journal of Family Psychology, 19(1), 111–120. https://doi.org/10.1037/0893-3200.19.1.111