Standard Deviation ใน Excel: ฟังก์ชัน STDEV.S, STDEV.P และสูตรการคำนวณ

การคำนวณ Standard Deviation ใน Excel เป็นสิ่งสำคัญสำหรับการวัดความแปรปรวนและการกระจายของข้อมูล Excel มีฟังก์ชัน Standard Deviation หลายตัว ได้แก่ STDEV.S สำหรับข้อมูล Sample (ใช้บ่อยที่สุด), STDEV.P สำหรับข้อมูล Population และฟังก์ชันเวอร์ชันเก่า STDEV/STDEVP คู่มือฉบับสมบูรณ์นี้ครอบคลุมสูตร Standard Deviation ทั้งหมดใน Excel เวลาที่ควรใช้แต่ละฟังก์ชัน และตัวอย่างทีละขั้นตอนพร้อมการตีความผล

ใช้ =STDEV.S(range) สำหรับ Sample Standard Deviation หรือ =STDEV.P(range) สำหรับ Population Standard Deviation ดาวน์โหลดไฟล์ Excel ฝึกปฏิบัติจากแถบด้านข้างเพื่อทำตามตัวอย่างจริง

ตารางอ้างอิงด่วน: สูตร Standard Deviation ใน Excel

ฟังก์ชัน	ใช้สำหรับ	Syntax	ตัวอย่าง
STDEV.S	Sample (ใช้บ่อยที่สุด)	`=STDEV.S(range)`	`=STDEV.S(A2:A50)`
STDEV.P	Population	`=STDEV.P(range)`	`=STDEV.P(A2:A50)`
STDEVA	Sample + logical values	`=STDEVA(range)`	`=STDEVA(A2:A50)`
STDEVPA	Population + logical values	`=STDEVPA(range)`	`=STDEVPA(A2:A50)`

ใช้ STDEV.S ใน 95% ของกรณี - เป็นตัวเลือกที่ถูกต้องเมื่อทำงานกับข้อมูล Sample จาก Population ที่ใหญ่กว่า

หากคุณไม่แน่ใจเกี่ยวกับความแตกต่างระหว่าง Population และ Sample Standard Deviation อ่านคู่มือนั้นก่อนเพื่อทำความเข้าใจว่าสูตรใดเหมาะกับข้อมูลของคุณ

ทำความเข้าใจสูตร Standard Deviation

Standard Deviation วัดว่าค่าแต่ละค่าเบียงเบนจาก Mean (ค่าเฉลี่ย) มากน้อยเพียงใด มีสูตรที่แตกต่างกัน 2 แบบขึ้นอยู่กับว่าข้อมูลของคุณเป็น:

Sample (n) - ชุดข้อมูลย่อยจาก Population ที่ใหญ่กว่า
Population (N) - กลุ่มทั้งหมดที่คุณกำลังศึกษา

สูตร Population Standard Deviation

Population Standard Deviation (σ) ใช้เมื่อคุณมีข้อมูลทั้งหมดของ Population:

\Large \sigma = \sqrt{\frac{\sum(x_i - \mu)^2}{N}}

โดยที่:

σ = Population Standard Deviation
Σ = ผลรวมของพจน์ต่อไปนี้
x_i = แต่ละค่าในชุดข้อมูล
μ = Population Mean
N = จำนวนค่าทั้งหมดใน Population

สูตร Sample Standard Deviation

Sample Standard Deviation (s) ใช้เมื่อคุณมีข้อมูลจากSample ของ Population ที่ใหญ่กว่า:

\Large s = \sqrt{\frac{\sum(x_i - \bar{x})^2}{n-1}}

โดยที่:

s = Sample Standard Deviation
Σ = ผลรวมของพจน์ต่อไปนี้
x_i = แต่ละค่าใน Sample
x̄ = Sample Mean
n-1 = degrees of freedom (Bessel's Correction)

ความแตกต่างสำคัญคือการหารด้วย n-1 แทนที่จะเป็น N เพื่อแก้ไข bias เมื่อประมาณค่า Population Parameters จากข้อมูล Sample

วิธีคำนวณ Population Standard Deviation ใน Excel

Excel มีฟังก์ชัน 2 ตัวสำหรับคำนวณ Population Standard Deviation:

ฟังก์ชัน STDEV.P

ฟังก์ชัน STDEV.P คำนวณ Population Standard Deviation และจะเพิกเฉยข้อความและ logical values (TRUE/FALSE) โดยอัตโนมัติ

Syntax:

=STDEV.P(number1, [number2], ...)

ตัวอย่าง:

สมมติคุณมีข้อมูลของ Population ทั้งหมดใน cells C2:C11 นี่คือวิธีคำนวณ Population Standard Deviation ทีละขั้นตอน:

ขั้นตอนที่ 1: เข้าถึง Insert Function dialog โดยคลิกปุ่ม "fx" หรือกด Shift+F3

ขั้นตอนที่ 2: พิมพ์ "STDEV.P" ใน search field และคลิก Go จากนั้นเลือก STDEV.P จากรายการ:

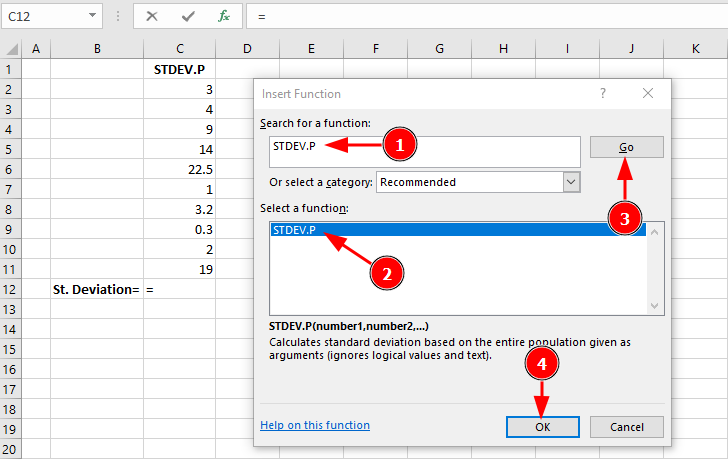หน้าต่าง Insert Function ของ Excel แสดงการเลือกฟังก์ชัน STDEV.P พร้อม search field และคำอธิบายฟังก์ชัน การค้นหาและเลือกฟังก์ชัน STDEV.P ใน Excel

ขั้นตอนที่ 3: ใน Function Arguments dialog เลือก data range ของคุณ (C2:C11):

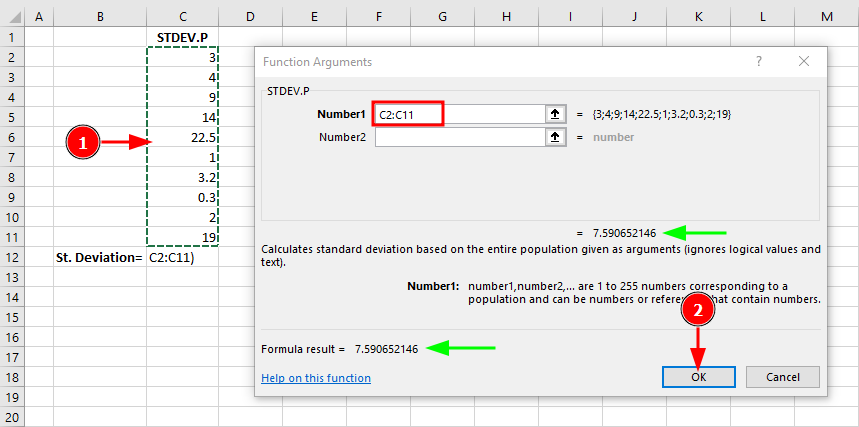หน้าต่าง Function Arguments ของ STDEV.P พร้อม data range และผลลัพธ์

ขั้นตอนที่ 4: คลิก OK เพื่อดูผลลัพธ์สุดท้าย:

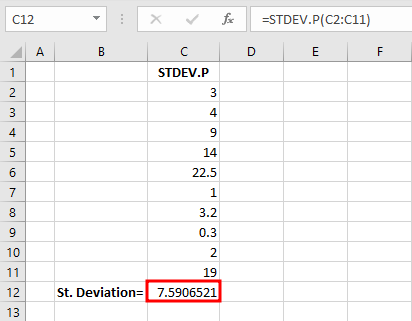สเปรดชีต Excel แสดงผลลัพธ์สูตร STDEV.P เท่ากับ 7.59 ใน cell C12 การคำนวณ STDEV.P ที่สำเร็จแสดง Population Standard Deviation

ฟังก์ชันส่งคืนค่า 7.59 เป็น Population Standard Deviation แสดงให้เห็นว่าค่าต่างๆ กระจายออกจาก Mean มากน้อยเพียงใด

ฟังก์ชัน STDEVPA

ฟังก์ชัน STDEVPA ก็คำนวณ Population Standard Deviation เช่นกัน แต่รวมข้อความและ logical values ด้วย:

Text และ FALSE = 0
TRUE = 1

Syntax:

=STDEVPA(value1, [value2], ...)

ตัวอย่าง:

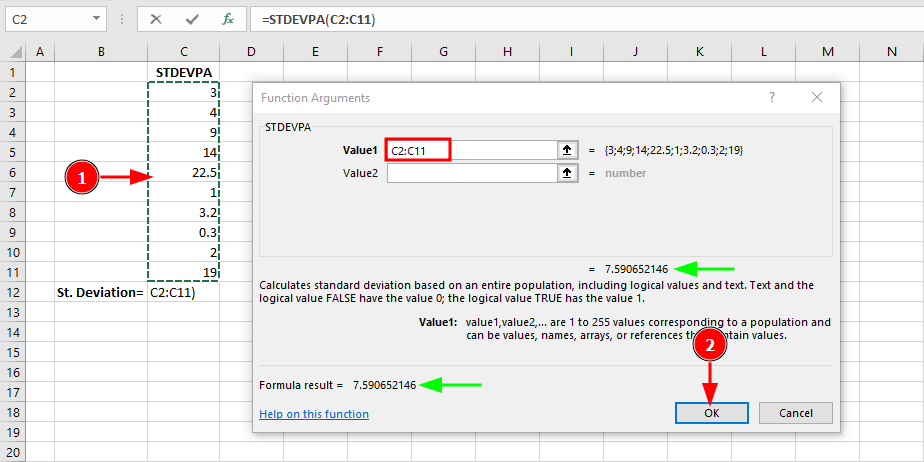หน้าต่าง Function Arguments ของ Excel สำหรับ STDEVPA แสดง data range และผลลัพธ์ 7.59 พร้อมคำอธิบายว่ารวม logical values ฟังก์ชัน STDEVPA รวม logical values และข้อความในการคำนวณ

ใช้ STDEVPA เมื่อชุดข้อมูลของคุณมี logical values ที่ต้องการนับในการคำนวณโดยเจตนา ในตัวอย่างนี้เนื่องจากชุดข้อมูลมีเฉพาะตัวเลข STDEVPA จึงคืนผลลัพธ์เดียวกับ STDEV.P (7.59)

วิธีคำนวณ Sample Standard Deviation ใน Excel

สำหรับสถานการณ์จริงส่วนใหญ่ คุณกำลังทำงานกับ Sample (ไม่ใช่ Population ทั้งหมด) Excel มีฟังก์ชัน 2 ตัวสำหรับ Sample Standard Deviation:

ฟังก์ชัน STDEV.S (ใช้บ่อยที่สุด)

ฟังก์ชัน STDEV.S คำนวณ Sample Standard Deviation และเป็นฟังก์ชันที่ใช้บ่อยที่สุด จะเพิกเฉยข้อความและ logical values

Syntax:

=STDEV.S(number1, [number2], ...)

ตัวอย่าง:

นี่คือวิธีคำนวณ Sample Standard Deviation โดยใช้ชุดข้อมูลเดียวกัน (C2:C11) ซึ่งตอนนี้เป็น Sample จาก Population ที่ใหญ่กว่า:

ขั้นตอนที่ 1: เข้าถึง Insert Function dialog และค้นหา "STDEV.S":

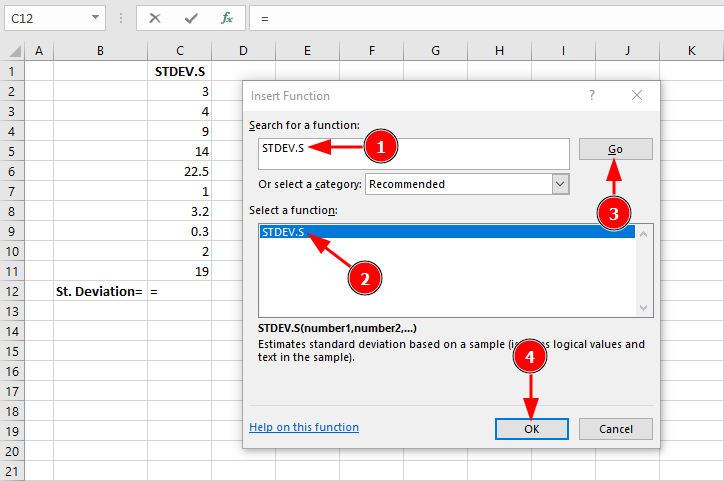หน้าต่าง Insert Function ของ Excel แสดงการเลือกฟังก์ชัน STDEV.S พร้อมคำอธิบายเกี่ยวกับ Sample Standard Deviation การเลือกฟังก์ชัน STDEV.S สำหรับ Sample Standard Deviation

ขั้นตอนที่ 2: ใน Function Arguments dialog เลือก data range ของคุณ:

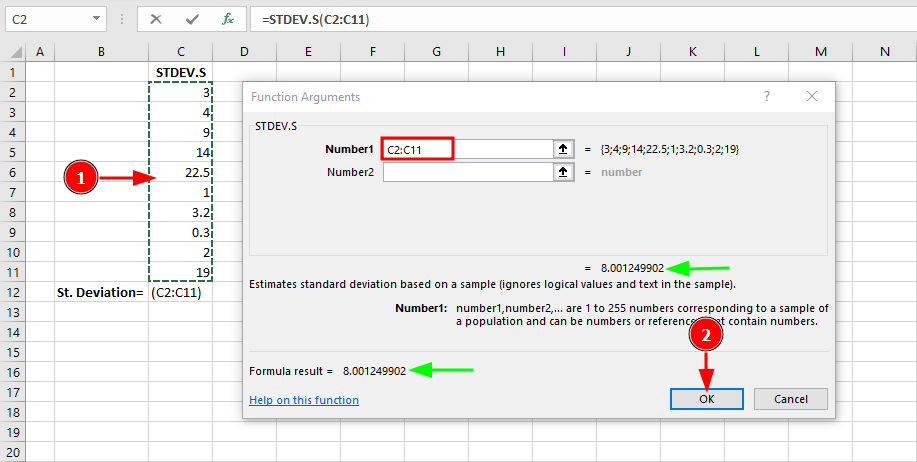หน้าต่าง Function Arguments ของ Excel สำหรับ STDEV.S แสดง data range C2:C11 และผลลัพธ์ 8.00 STDEV.S คืนค่า 8.00 (สูงกว่า STDEV.P เนื่องจาก Bessel's Correction n-1)

สังเกตว่าผลลัพธ์คือ 8.00 สำหรับ Sample Standard Deviation เทียบกับ 7.59 สำหรับ Population Standard Deviation ความแตกต่างนี้เกิดจาก Bessel's Correction (การหารด้วย n-1 แทนที่จะเป็น N) ซึ่งให้การประมาณที่ไม่มี bias เมื่อทำงานกับข้อมูล Sample

นี่คือตัวเลือกเริ่มต้นสำหรับการวิเคราะห์ทางสถิติส่วนใหญ่เมื่อทำงานกับข้อมูล Sample

ฟังก์ชัน STDEVA

ฟังก์ชัน STDEVA คำนวณ Sample Standard Deviation แต่รวมข้อความและ logical values ด้วย:

Text และ FALSE = 0
TRUE = 1

Syntax:

=STDEVA(value1, [value2], ...)

ตัวอย่าง:

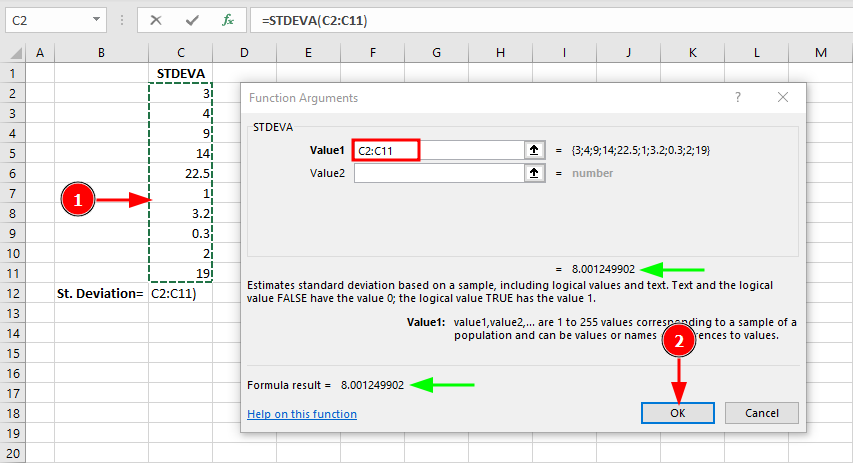หน้าต่าง Function Arguments ของ Excel สำหรับ STDEVA แสดง data range และผลลัพธ์ 8.00 พร้อมคำอธิบายเกี่ยวกับการรวม logical values ฟังก์ชัน STDEVA รวม logical values และข้อความในการคำนวณ Sample Standard Deviation

ใช้ STDEVA เมื่อคุณต้องการรวม logical values ในการคำนวณโดยเฉพาะเท่านั้น ในตัวอย่างนี้ที่มีข้อมูลเป็นตัวเลขล้วนๆ STDEVA คืนผลลัพธ์เดียวกับ STDEV.S (8.00)

ฟังก์ชัน Standard Deviation เวอร์ชันเก่า

Excel ยังมีฟังก์ชันรุ่นเก่าเพื่อความเข้ากันได้แบบย้อนหลัง:

ฟังก์ชันเวอร์ชันเก่า	ฟังก์ชันสมัยใหม่ที่เทียบเท่า	Use Case
STDEV	STDEV.S	Sample Standard Deviation
STDEVP	STDEV.P	Population Standard Deviation

คำแนะนำ: ใช้ฟังก์ชันสมัยใหม่เสมอ (STDEV.S, STDEV.P) เพราะจะชัดเจนกว่าว่าคุณกำลังคำนวณ Sample หรือ Population Standard Deviation

ควรใช้ฟังก์ชัน Standard Deviation ตัวไหน?

นี่คือคู่มือการตัดสินใจอย่างรวดเร็ว:

ใช้ STDEV.S เมื่อ:

ทำงานกับ Sample จาก Population ที่ใหญ่กว่า (กรณีที่พบบ่อยที่สุด)
ทำการสำรวจ การทดลอง หรือการศึกษาการสุ่มตัวอย่าง
คุณมีชุดข้อมูลย่อยที่เป็นตัวแทนของกลุ่มที่ใหญ่กว่า
ตัวอย่าง: คะแนนสอบจากนักเรียน 30 คนจากนักเรียนทั้งหมด 500 คน

ใช้ STDEV.P เมื่อ:

คุณมีข้อมูลสำหรับ Population ทั้งหมด
ชุดข้อมูลของคุณรวมสมาชิกทุกคนในกลุ่ม
ตัวอย่าง: คะแนนสอบสำหรับนักเรียนทั้งหมด 30 คนในชั้นเรียนที่สมบูรณ์

ใช้ STDEVPA/STDEVA เมื่อ:

ชุดข้อมูลของคุณมีค่า TRUE/FALSE หรือข้อความโดยเจตนา
คุณต้องการให้ค่าเหล่านี้ถูกนับเป็น 1 และ 0 ตามลำดับ

กฎทั่วไป: หากคุณไม่แน่ใจ ใช้ STDEV.S (Sample) เป็นตัวเลือกที่อนุรักษ์นิยมทางสถิติและเหมาะสมสำหรับการวิเคราะห์ส่วนใหญ่

ตัวอย่างทีละขั้นตอน: การคำนวณ Standard Deviation

มาดูตัวอย่างที่สมบูรณ์ของการคำนวณ Standard Deviation สำหรับข้อมูลยอดขายรายเดือน

ชุดข้อมูล: ตัวเลขยอดขายรายเดือน (หน่วยพัน) สำหรับ 12 เดือน

เดือน	ยอดขาย
ม.ค.	45
ก.พ.	52
มี.ค.	48
เม.ย.	61
พ.ค.	55
มิ.ย.	49
ก.ค.	58
ส.ค.	63
ก.ย.	51
ต.ค.	47
พ.ย.	54
ธ.ค.	59

ขั้นตอนที่ 1: ใส่ข้อมูลของคุณใน Excel (cells B2:B13)

ขั้นตอนที่ 2: คำนวณ Mean โดยใช้ =AVERAGE(B2:B13) ผลลัพธ์: 53.5

ขั้นตอนที่ 3: คำนวณ Sample Standard Deviation โดยใช้ =STDEV.S(B2:B13) ผลลัพธ์: 5.9

การตีความผล: ยอดขายรายเดือนเฉลี่ยคือ 53.5 พัน โดยมี Standard Deviation 5.9 พัน ซึ่งหมายความว่าเดือนส่วนใหญ่อยู่ภายในประมาณ 6 พันจากค่าเฉลี่ย (ประมาณระหว่าง 47.6 ถึง 59.4 พัน)

ฟังก์ชันทางสถิติที่เกี่ยวข้องใน Excel

VAR.S และ VAR.P (Variance)

Variance คือกำลังสองของ Standard Deviation Excel มีฟังก์ชัน Variance ที่ทำงานคล้ายกัน:

=VAR.S(number1, [number2], ...)  // Sample Variance
=VAR.P(number1, [number2], ...)  // Population Variance

ความสัมพันธ์: Standard Deviation = √Variance

เรียนรู้เพิ่มเติมเกี่ยวกับ Variance และสถิติเชิงพรรณนาอื่นๆ ใน Excel

AVEDEV (Average Deviation)

ฟังก์ชัน AVEDEV คำนวณค่าเฉลี่ยของค่าเบียงเบนสัมบูรณ์จาก Mean:

=AVEDEV(number1, [number2], ...)

คล้ายกับ Standard Deviation ค่า Average Deviation ที่สูงบ่งบอกถึงการกระจายสูงรอบ Mean ในขณะที่ค่าต่ำบ่งบอกถึงการกระจายต่ำ แตกต่างจาก Standard Deviation ที่ยกกำลังสองของค่าเบียงเบน AVEDEV ใช้ค่าสัมบูรณ์ทำให้ไม่ไวต่อค่าผิดปกติมากนัก

การตีความผลลัพธ์ Standard Deviation

การทำความเข้าใจว่าค่า Standard Deviation ของคุณหมายความว่าอย่างไร:

Standard Deviation ขนาดเล็ก (ใกล้ 0):

จุดข้อมูลจับกลุ่มแน่นรอบ Mean
ความแปรปรวนต่ำ
ค่ามีความสม่ำเสมอและคาดการณ์ได้
ตัวอย่าง: SD = 2 สำหรับคะแนนสอบเฉลี่ย 85 หมายความว่าคะแนนส่วนใหญ่อยู่ระหว่าง 83-87

Standard Deviation ขนาดใหญ่:

จุดข้อมูลกระจายออกจาก Mean
ความแปรปรวนสูง
ค่ามีความสม่ำเสมอน้อยกว่า
ตัวอย่าง: SD = 15 สำหรับคะแนนสอบเฉลี่ย 85 หมายความว่าคะแนนมีช่วงกว้าง (70-100)

ในการแจกแจงปกติ:

~68% ของค่าอยู่ภายใน 1 Standard Deviation จาก Mean
~95% ของค่าอยู่ภายใน 2 Standard Deviations
~99.7% ของค่าอยู่ภายใน 3 Standard Deviations

สำหรับข้อมูลเพิ่มเติมเกี่ยวกับ Measures of Central Tendency และการกระจาย ดูคู่มือของเราเกี่ยวกับ การคำนวณ Mean, Median และ Mode

ข้อผิดพลาดที่พบบ่อยที่ควรหลีกเลี่ยง

1. ใช้ STDEV.P สำหรับข้อมูล Sample

สิ่งนี้ประมาณค่าความแปรปรวนใน Sample ของคุณต่ำไป
ใช้ STDEV.S เสมอเมื่อทำงานกับ Samples

2. รวม headers ใน range ของคุณ

STDEV.S จะคืนค่า error หาก text headers ถูกรวมอยู่ด้วย
เลือกเฉพาะ cells ที่มีข้อมูลตัวเลข

3. ผสม Sample และ Population formulas

ต้องสม่ำเสมอ: ข้อมูล Sample ต้องใช้สูตร Sample ตลอดการวิเคราะห์ของคุณ

4. เพิกเฉยค่าผิดปกติ

ค่าที่สุดขั้วมีผลต่อ Standard Deviation อย่างมาก
พิจารณาลบค่าผิดปกติหรือใช้ Median/IQR สำหรับข้อมูลที่เบ้

คำถามที่พบบ่อย

ความแตกต่างระหว่าง STDEV.S และ STDEV.P คืออะไร?

STDEV.S คำนวณ Sample Standard Deviation (หารด้วย n-1) และใช้เมื่อข้อมูลของคุณเป็น Sample จาก Population ที่ใหญ่กว่า STDEV.P คำนวณ Population Standard Deviation (หารด้วย N) และใช้เมื่อคุณมีข้อมูลสำหรับ Population ทั้งหมด ใช้ STDEV.S สำหรับสถานการณ์จริงส่วนใหญ่ที่คุณทำงานกับข้อมูล Sample

ฉันจะรู้ได้อย่างไรว่าควรใช้ Sample หรือ Population Standard Deviation?

ใช้ Sample Standard Deviation (STDEV.S) เมื่อข้อมูลของคุณเป็นตัวแทนของชุดย่อยของกลุ่มที่ใหญ่กว่าที่คุณพยายามเข้าใจ ใช้ Population Standard Deviation (STDEV.P) เฉพาะเมื่อคุณมีทุกจุดข้อมูลจาก Population ที่สมบูรณ์ ตัวอย่างเช่น: การสำรวจลูกค้า 100 คนจาก 10,000 คน = Sample บันทึกคะแนนสอบสำหรับนักเรียนทั้งหมด 30 คนในชั้นเรียนที่สมบูรณ์ของคุณ = Population

Standard Deviation เท่ากับ 0 หมายความว่าอย่างไร?

Standard Deviation เท่ากับ 0 หมายความว่าไม่มีความแปรปรวนในข้อมูลของคุณ—ค่าทั้งหมดเหมือนกันทุกประการ ตัวอย่างเช่น หากคะแนนสอบทั้งหมดเป็น 85 Standard Deviation คือ 0 สิ่งนี้หายากในข้อมูลจริงและมักบ่งบอกถึง error ในการป้อนข้อมูลหรือว่าคุณกำลังวัดค่าคงที่

Standard Deviation สามารถเป็นลบได้หรือไม่?

ไม่ Standard Deviation ไม่สามารถเป็นลบได้เลย มันคำนวณเป็นรากที่สองของ Variance (ซึ่งเป็นค่าบวกหรือศูนย์เสมอ) ดังนั้นผลลัพธ์จึงเป็นศูนย์หรือบวกเสมอ หาก Excel คืนค่าลบ แสดงว่ามี error ในสูตรหรือข้อมูลของคุณ

ฉันจะคำนวณ Standard Deviation สำหรับหลายคอลัมน์พร้อมกันได้อย่างไร?

คุณสามารถคำนวณ Standard Deviation สำหรับแต่ละคอลัมน์แยกกันโดยใช้ STDEV.S ในแต่ละ Range: =STDEV.S(A2:A50) สำหรับคอลัมน์ A, =STDEV.S(B2:B50) สำหรับคอลัมน์ B เป็นต้น Excel ไม่มีฟังก์ชันในตัวเพื่อคำนวณ Standard Deviation ข้ามหลายคอลัมน์ที่ไม่อยู่ติดกันในสูตรเดียว

Bessel's Correction (n-1) คืออะไร?

Bessel's Correction คือการหารด้วย (n-1) แทนที่จะเป็น n เมื่อคำนวณ Sample Standard Deviation การแก้ไขนี้คำนึงถึง bias ที่เกิดขึ้นเมื่อประมาณค่า Population Parameters จากข้อมูล Sample มันให้การประมาณที่แม่นยำกว่า (ไม่มี bias) ของ Population Standard Deviation ที่แท้จริง STDEV.S ใช้การแก้ไขนี้โดยอัตโนมัติ

ฉันจะคำนวณ Standard Deviation สำหรับข้อมูลที่จัดกลุ่มหรือตารางความถี่ได้อย่างไร?

สำหรับข้อมูลที่จัดกลุ่มพร้อมความถี่ คูณแต่ละค่าด้วยความถี่ของมัน จากนั้นใช้ array formulas หรือสร้างชุดข้อมูลที่ขยาย ตัวอย่างเช่น หากค่า 10 ปรากฏ 5 ครั้ง ให้แสดงรายการ 5 ครั้งหรือใช้: =SQRT(SUMPRODUCT((values-AVERAGE(values))^2, frequencies)/SUM(frequencies)) สำหรับ Population หรือหารด้วย (SUM(frequencies)-1) สำหรับ Sample

สรุป

การคำนวณ Standard Deviation ใน Excel เป็นเรื่องตรงไปตรงมาเมื่อคุณเข้าใจว่าควรใช้ฟังก์ชันใด สำหรับการวิเคราะห์ส่วนใหญ่ที่เกี่ยวข้องกับข้อมูล Sample STDEV.S เป็นฟังก์ชันหลักของคุณ ในขณะที่ STDEV.P สงวนไว้สำหรับชุดข้อมูล Population ที่สมบูรณ์

การทำความเข้าใจ Standard Deviation เป็นสิ่งสำคัญสำหรับการวิเคราะห์ความแปรปรวนในข้อมูลของคุณและเป็นรากฐานสำหรับการวิเคราะห์ทางสถิติขั้นสูงยิ่งขึ้น เมื่อรวมกับ Mean, Median และ Mode Standard Deviation ให้ภาพรวมที่สมบูรณ์ของการแจกแจงข้อมูลของคุณ

ฝึกฝนด้วยไฟล์ Excel ที่ดาวน์โหลดได้เพื่อสร้างความมั่นใจในการคำนวณและตีความ Standard Deviation สำหรับชุดข้อมูลของคุณเอง สำหรับเครื่องมือทางสถิติเพิ่มเติมใน Excel สำรวจคู่มือของเราเกี่ยวกับ การเพิ่ม Data Analysis ToolPak