สูตร Standard Deviation แบบ Population กับ Sample: คู่มือฉบับสมบูรณ์

•By Leonard Cucos•th
สถิติเชิงพรรณนาสถิติวิธีวิจัย

ในบทเรียนนี้ เราจะเปรียบเทียบสูตร Standard Deviation แบบ Population กับ Sample และวิธีการคำนวณสมการทั้งสองด้วยมือทีละขั้นตอน

Standard Deviation ต้องใช้ค่าเฉลี่ย (Mean) ของ Population หรือ Sample ที่เราวัด เราจะสาธิตวิธีคำนวณค่า Mean สำหรับชุดข้อมูลโดยใช้ตัวอย่างทีละขั้นตอน

บทเรียนนี้ยังสาธิตวิธีคำนวณ Variance จาก Standard Deviation โดยใช้ความสัมพันธ์ทางคณิตศาสตร์อย่างง่าย

Standard Deviation คืออะไร? ความหมายและคำอธิบาย

Standard Deviation วัดระดับการกระจายตัวของคะแนนในชุดข้อมูลเมื่อเทียบกับค่าเฉลี่ยของคะแนนเหล่านั้น กล่าวอีกนัยหนึ่ง Standard Deviation วัดระดับการกระจายของกลุ่มข้อมูลเมื่อเทียบกับค่า Mean ยิ่งข้อมูลกระจายตัวมาก ค่า Standard Deviation ก็จะยิ่งสูง Standard Deviation เป็นองค์ประกอบพื้นฐานในกระบวนการทางสถิติหลายอย่าง รวมถึงการวิเคราะห์ Correlation และการทดสอบสมมติฐาน

เพื่อให้แน่ใจว่าเราเข้าใจแนวคิดนี้ ลองคิดถึงชุดตัวเลขสองชุดต่อไปนี้: 2, 3, 4 และ 2, 4, 6

ชุดตัวเลขใดมี Standard Deviation สูงกว่า?

คุณตอบถูกแล้ว: กลุ่มที่สองประกอบด้วยตัวเลข 2, 4 และ 6 แต่ทำไม? ลองเปรียบเทียบกลุ่มเหล่านี้โดยใช้เส้นจำนวน

เส้นจำนวนแสดงการกระจายตัวของค่า 2, 3, 4 และ 2, 4, 6 เพื่อแสดง Standard Deviation การเปรียบเทียบเส้นจำนวนแสดงการกระจายตัวของค่าสำหรับการคำนวณ Standard Deviation

Standard Deviation สำหรับกลุ่มตัวเลขที่สอง (2, 4, 6) ต้องสูงกว่า เพราะค่าต่างๆ บนเส้นจำนวนกระจายตัวมากกว่า ในทางตรงกันข้าม ตัวเลขในกลุ่มแรก (2, 3, 4) อยู่ใกล้กันมากกว่า ดังนั้น Standard Deviation จึงต้องต่ำกว่า

แต่เราจะพิสูจน์ว่าเราคิดถูกได้อย่างไร? ท้ายที่สุดแล้ว ชุดข้อมูลอาจมีหลายร้อยหรือหลายพันค่า

คำตอบคือ ตามที่คุณอาจเดาได้ เราใช้สมการ Standard Deviation

ก่อนที่เราจะลงมือฝึกทักษะทางคณิตศาสตร์ โปรดจำไว้ว่ามีสมการสองแบบสำหรับ Standard Deviation คือ:

  • สูตร Population Standard Deviation คำนวณ Standard Deviation สำหรับ Population ทั้งหมด และต้องการค่า Population Mean
  • สูตร Sample Standard Deviation ใช้คำนวณ Standard Deviation สำหรับกลุ่มตัวอย่างของ Population และต้องการค่า Sample Mean

นี่คือการเปรียบเทียบสองสูตรแบบเคียงข้างกัน โดยความแตกต่างถูกเน้นด้วยสีแดง

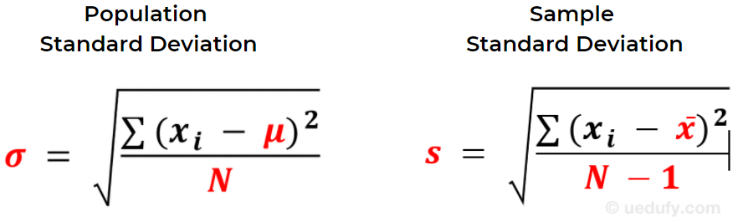การเปรียบเทียบสูตร Population และ Sample Standard Deviation แบบเคียงข้างกันพร้อมเน้นความแตกต่าง การเปรียบเทียบสูตร Population vs. Sample Standard Deviation

สัญลักษณ์ Population vs Sample Standard Deviation (σ vs s)

สัญลักษณ์ที่ใช้แตกต่างกันระหว่างสูตร Population และ Sample Standard Deviation:

สัญลักษณ์ Population Standard Deviation:

  • σ (ตัวอักษรกรีก sigma ตัวพิมพ์เล็ก) = Population Standard Deviation
  • μ (ตัวอักษรกรีก mu ตัวพิมพ์เล็ก) = Population Mean
  • N = จำนวนค่าทั้งหมดใน Population

สัญลักษณ์ Sample Standard Deviation:

  • s (ตัวอักษร s ตัวพิมพ์เล็ก) = Sample Standard Deviation
  • x̄ (x-bar) = Sample Mean
  • N-1 = ขนาด Sample ลบด้วย 1 (Bessel's Correction)

ทั้งสองสูตรคำนวณ Standard Deviation โดยใช้แนวทางพื้นฐานเดียวกัน โดยมีความแตกต่างสำคัญในสัญลักษณ์และตัวหาร (N vs N-1) ซึ่งเราจะสาธิตรายละเอียดต่อไป

สูตร Population Standard Deviation

ตามชื่อที่บอกไว้ สมการต่อไปนี้ใช้คำนวณ Standard Deviation สำหรับ Population ที่กำหนด

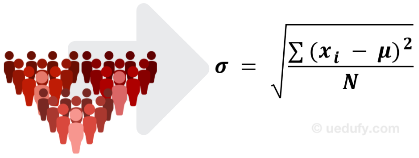สูตร Population Standard Deviation ด้วยสัญลักษณ์กรีก sigma, mu และเครื่องหมาย summation สูตร Population Standard Deviation

โดยที่:

  • σ = สัญลักษณ์สำหรับ Population Standard Deviation
  • Σ = ผลรวมของพจน์ต่อไปนี้
  • xi = ทุกจุดข้อมูลในชุดข้อมูล (observation หรือสมาชิกของ Population)
  • μ = Population Mean
  • N = จำนวนค่าใน Population

ตอนนี้มารวมทุกอย่างเข้าด้วยกัน นี่คือวิธีอ่านสูตร Population Standard Deviation: Standard Deviation (σ) เท่ากับรากที่สองของผลรวม (Σ) ของความแตกต่างกำลังสองทั้งหมดระหว่างทุกจุดข้อมูล xi ในชุดข้อมูลกับ Population Mean (μ) หารด้วยจำนวนค่าทั้งหมดในชุด (N)

ต่อไป มาคำนวณ Standard Deviation สำหรับชุดตัวเลข 3, 4, และ 5 โดยใช้สูตร Population Standard Deviation

ขั้นตอนที่ 1: หาค่า Mean (μ)

เพื่อหาค่า Mean ของสมาชิกทั้งหมดใน Population เพียงคำนวณผลรวมของค่าทั้งหมด จากนั้นหารผลรวมด้วยจำนวนค่าในชุดข้อมูล นี่คือค่า Mean สำหรับชุดตัวเลข 3, 4 และ 5

μ=3+4+53=123=4\mu=\frac{3+4+5}{3}=\frac{12}{3}=4

เคล็ดลับ: เมื่อชุดตัวเลขห่างกันเท่าๆ กัน ค่า Mean จะเป็นตัวเลขตรงกลาง ตัวอย่างเช่น สำหรับชุดตัวเลข 2, 5, 7, 9, 12 ค่า Mean คือ 7

ขั้นตอนที่ 2: คำนวณสูตร Standard Deviation สำหรับ Population

σ=∑(xi−μ)2N\sigma=\sqrt{\frac{\sum\left(x_{i}-\mu\right)^{2}}{N}}

สำหรับชุดตัวเลข 3, 4 และ 5 ทุกจุดข้อมูล xi = x3, x4, x5 ค่า Mean μ = 4 ตามที่คำนวณข้างต้น และ Population N = 3 (เนื่องจากเรามีสามค่าในชุดข้อมูล) มาใส่ตัวเลขเหล่านี้ในสมการ Population Standard Deviation:

σ=(3−4)2+(4−4)2+(5−4)23\sigma=\sqrt{\frac{(3-4)^{2}+(4-4)^{2}+(5-4)^{2}}{3}}

ขั้นตอนที่ 3: คำนวณผลรวมของทุกจุดข้อมูล

σ=1+0+13\sigma=\sqrt{\frac{1+0+1}{3}}

ขั้นตอนที่ 4: แก้รากที่สอง

σ=23=0.66=0.81\sigma=\sqrt{\frac{2}{3}}=\sqrt{0.66}=0.81

Population Standard Deviation สำหรับชุดตัวเลข 3, 4 และ 5 คือ 0.81

แบบฝึกหัด: ใช้สูตร Population Standard Deviation และทำตามตัวอย่างข้างต้น คำนวณ Standard Deviation สำหรับชุดตัวเลข 2, 4 และ 6 Standard Deviation สูงหรือต่ำกว่า 0.81?

อย่างไรก็ตาม มีปัญหาสำคัญกับ Sample แม้ว่าค่าเฉลี่ยของ Population จะคงที่ (เราคำนวณค่า Mean สำหรับสมาชิกทั้งหมดของ Population เสมอ) แต่ Sample แต่ละชุดอาจแตกต่างกัน

ตัวอย่างเช่น หากเราหลับตาและหยิบ Sample แบบสุ่มสองสามชุดที่ประกอบด้วย 5 ตัวเลขจากถ้วยที่มีตัวเลขหนึ่งร้อยตัว ทุก Sample มักจะมีตัวเลขที่แตกต่างกัน ดังนั้น Sample Mean จะแตกต่างกันระหว่าง Sample ด้วย

แล้วเราจะทำให้แน่ใจได้อย่างไรว่า Sample ที่เราหยิบนั้นเป็นตัวแทนของ Population ที่สุ่มตัวอย่างมา? นั่นคือStandard Error อีกคำศัพท์ทางสถิติหนึ่ง เราจะไม่ครอบคลุม Standard Error เนื่องจากบทความที่ลิงก์ไว้ข้างต้นมีทุกอย่างที่คุณต้องรู้เกี่ยวกับมันแล้ว

สูตร Sample Standard Deviation

แต่จะเกิดอะไรขึ้นเมื่อเราไม่สามารถเข้าถึง Population ทั้งหมด แต่มีเพียง Sample เพื่อคำนวณค่า Mean? นี่เป็นกรณีที่พบบ่อยในการวิจัยทางสังคมศาสตร์ และโชคดีสำหรับเรา สูตร Sample Standard Deviation ไม่แตกต่างจากสูตรที่ใช้สำหรับ Population มากนัก

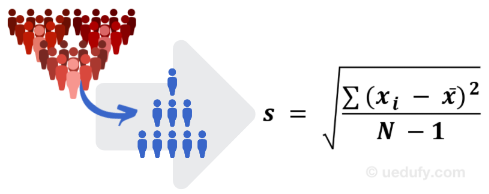สูตร Sample Standard Deviation พร้อมสัญลักษณ์ s, x-bar และตัวหาร N-1 สูตร Sample Standard Deviation

โดยที่:

  • s = สัญลักษณ์สำหรับ Sample Standard Deviation
  • Σ = ผลรวมของพจน์ต่อไปนี้
  • xi = ทุกจุดข้อมูลในชุดข้อมูล (observation หรือสมาชิกของ Population)
  • x̄ = Sample Mean
  • N-1 = จำนวนค่าใน Sample (N) ลบ 1

และนี่คือวิธีอ่านสมการข้างต้น: Sample Standard Deviation (s) เท่ากับรากที่สองของผลรวม (Σ) ของความแตกต่างกำลังสองระหว่างทุกจุดข้อมูล (xi) ใน Sample กับ Sample Mean (x̄) หารด้วย N – 1

ความแตกต่างง่ายต่อการสังเกตระหว่างสูตร Population และ Sample Standard Deviation ความแตกต่างที่ชัดเจนอย่างหนึ่งคือสัญลักษณ์สำหรับ Sample Mean x̄ ในขณะที่ Population Mean ใช้ μ ความแตกต่างอีกอย่างคือเราหารทุกอย่างด้วย N – 1

คำนวณ Sample Standard Deviation ก็เหมือนกับ Population Standard Deviation เกือบทั้งหมด แต่ลองทำอีกครั้ง คครั้งนี้เราจะใช้ชุดค่าที่สองจากเส้นจำนวนของเรา: 2, 4 และ 6

ขั้นตอนที่ 1: คำนวณ Sample Mean (x̄)

ขั้นตอนนี้เหมือนกับการหาค่าเฉลี่ย Population ในตัวอย่างก่อนหน้า Sample Mean สำหรับชุดตัวเลข 2, 4 และ 6 คือ 4 นี่คือการพิสูจน์:

xˉ=2+4+63=123=4\bar{x}=\frac{2+4+6}{3}=\frac{12}{3}=4

ขั้นตอนที่ 2: คำนวณสูตร Sample Standard Deviation

s=∑(xi−xˉ)2N−1s=\sqrt{\frac{\sum\left(x_{i}-\bar{x}\right)^{2}}{N-1}}

ต่อไป ใส่ค่าในสมการ Sample Standard Deviation:

s=(2−4)2+(4−4)2+(6−4)23−1s=\sqrt{\frac{(2-4)^{2}+(4-4)^{2}+(6-4)^{2}}{3-1}}

ขั้นตอนที่ 3: แก้รากที่สอง

s=4+0+42=4=2s=\sqrt{\frac{4+0+4}{2}}=\sqrt{4}=2

Sample Standard Deviation สำหรับชุดตัวเลข 2, 4 และ 6 คือ 2

แบบฝึกหัด:

ใช้สูตร Sample Standard Deviation และทำตามตัวอย่างข้างต้น คำนวณ Standard Deviation สำหรับชุดตัวเลข 2, 5, 7, 9 และ 12 เพื่อให้ง่ายขึ้น ค่า Mean คือ 7

เมื่อใดควรใช้ Population vs Sample Standard Deviation

การเลือกระหว่าง Population และ Sample Standard Deviation ขึ้นอยู่กับชุดข้อมูลของคุณ:

ใช้ Population Standard Deviation (σ) เมื่อ:

  • คุณมีข้อมูลสำหรับทุกสมาชิกของ Population
  • คุณกำลังวิเคราะห์ชุดข้อมูลที่สมบูรณ์และมีขอบเขตจำกัด
  • คุณต้องการอธิบายความแปรปรวนจริงของชุดข้อมูลทั้งหมดของคุณ
  • ตัวอย่าง: คะแนนสอบของนักเรียนทั้งหมดในห้องเรียนเดียว

ใช้ Sample Standard Deviation (s) เมื่อ:

  • คุณกำลังทำงานกับส่วนย่อยของ Population ที่ใหญ่กว่า
  • คุณต้องการประมาณ Population Parameters จากข้อมูล Sample
  • คุณกำลังทำการวิจัยที่การเก็บข้อมูล Population ทั้งหมดเป็นไปไม่ได้
  • ตัวอย่าง: คำตอบแบบสำรวจจาก 500 คนเพื่อประมาณความคิดเห็นของผู้อยู่อาศัย 50,000 คน

ในการวิจัยและสถิติ Sample Standard Deviation ได้รับความนิยมมากกว่าเนื่องจากการเข้าถึง Population ทั้งหมดแทบจะเป็นไปไม่ได้ ตัวหาร N-1 ในสูตร Sample ให้การประมาณค่า Population Standard Deviation ที่ไม่มีอคติ สำหรับการคำนวณในทางปฏิบัติ คุณสามารถใช้ฟังก์ชันในตัวของ Excel เพื่อคำนวณทั้ง Population และ Sample Standard Deviation โดยอัตโนมัติ

วิธีคำนวณ Variance จาก Standard Deviation

Standard Deviation และ Variance เป็นมาตรวัดการกระจายที่เกี่ยวข้องกันอย่างใกล้ชิด ในขณะที่ Standard Deviation แสดงระดับการกระจายของค่าจาก Mean Variance แทนค่าระยะทางกำลังสองเฉลี่ยของแต่ละจุดจาก Mean Variance เป็นพื้นฐานสำหรับการทดสอบทางสถิติหลายอย่าง รวมถึง ANOVA และการวิเคราะห์ Regression

ความสัมพันธ์ระหว่าง Standard Deviation และ Variance ชัดเจนเมื่อมองวิธีคำนวณ Variance หากเรารู้ Standard Deviation สำหรับ Population หรือ Sample สิ่งที่เราต้องทำคือยกกำลังสองเพื่อหา Variance

σ2=∑(xi−μ)2N\sigma^{2}={\frac{\sum\left(x_{i}-\mu\right)^{2}}{N}}

ตัวอย่างเช่น ผลลัพธ์ Population Standard Deviation ที่เราคำนวณก่อนหน้านี้คือ σ = 0.81 ดังนั้นเราสามารถคำนวณ Population Variance จากมันได้: 0.81² = 0.6561 Variance สำหรับชุดตัวเลข 3, 4, และ 5 คือ 0.6561

สามารถทำเช่นเดียวกันเพื่อคำนวณ Variance สำหรับ Sample โดยใช้สมการต่อไปนี้:

s2=∑(xi−xˉ)2N−1s^{2}={\frac{\sum\left(x_{i}-\bar{x}\right)^{2}}{N-1}}

ดังนั้นเพื่อหา Variance สำหรับ Sample ที่เราคำนวณก่อนหน้านี้ สิ่งที่เราต้องการคือยกกำลังสอง Sample Standard Deviation: s² = 2² = 4 สำหรับการใช้งานใน Excel โปรดดูคู่มือของเราเกี่ยวกับวิธีการคำนวณ Standard Deviation ด้วย Excel สำหรับทั้ง Population และ Sample

คำถามที่พบบ่อยเกี่ยวกับ Population และ Sample Standard Deviation

Population Standard Deviation (σ) คำนวณความแปรปรวนสำหรับ Population ทั้งหมดโดยหารด้วย N ในขณะที่ Sample Standard Deviation (s) ประมาณความแปรปรวนของ Population จาก Sample โดยหารด้วย N-1 ตัวหาร N-1 แก้ไขอคติเมื่อประมาณ Population Parameters จากข้อมูล Sample
ใช้ Population Standard Deviation เมื่อคุณมีข้อมูลสำหรับทุกสมาชิกของ Population ใช้ Sample Standard Deviation เมื่อทำงานกับส่วนย่อยของ Population เพื่อประมาณ Population Parameters ในการวิจัย Sample Standard Deviation ได้รับความนิยมมากที่สุดเนื่องจากการเก็บข้อมูลจาก Population ทั้งหมดแทบจะเป็นไปไม่ได้
สัญลักษณ์สำหรับ Population Standard Deviation คือตัวอักษรกรีก sigma (σ) Population Mean แทนด้วย mu (μ) และ N แทนจำนวนค่าทั้งหมดใน Population
สัญลักษณ์สำหรับ Sample Standard Deviation คือตัวอักษรพิมพ์เล็ก s Sample Mean แทนด้วย x̄ (x-bar) และตัวหารใช้ N-1 แทน N เพื่อแก้ไขอคติของ Sample
การหารด้วย N-1 แทน N ให้การประมาณค่า Population Standard Deviation จากข้อมูล Sample ที่ไม่มีอคติ การแก้ไขนี้เรียกว่า Bessel's Correction คำนึงถึงข้อเท็จจริงที่ว่าข้อมูล Sample มักจะประมาณความแปรปรวนของ Population ต่ำไป การปรับ N-1 เพิ่ม Standard Deviation ที่คำนวณได้เล็กน้อยเพื่อประมาณค่า Population จริงได้ดีขึ้น
Variance เท่ากับ Standard Deviation ยกกำลังสอง สำหรับ Population Variance: σ² = (Standard Deviation)² สำหรับ Sample Variance: s² = (Standard Deviation)² ในทางกลับกัน Standard Deviation เท่ากับรากที่สองของ Variance

สรุป

การทำความเข้าใจความแตกต่างระหว่าง Population และ Sample Standard Deviation เป็นพื้นฐานสำหรับการวิเคราะห์ทางสถิติ Population Standard Deviation (σ) ใช้เมื่อวิเคราะห์ชุดข้อมูลที่สมบูรณ์ ในขณะที่ Sample Standard Deviation (s) ใช้เมื่อทำงานกับส่วนย่อยเพื่อประมาณ Population Parameters

ความแตกต่างสำคัญอยู่ที่สัญลักษณ์และวิธีการคำนวณ Population Standard Deviation ใช้ μ สำหรับ Mean และหารด้วย N ในขณะที่ Sample Standard Deviation ใช้ x̄ และหารด้วย N-1 เพื่อแก้ไขอคติการประมาณค่า การปรับ N-1 นี้เรียกว่า Bessel's Correction ช่วยให้มั่นใจว่าสถิติ Sample ให้การประมาณค่า Population Parameters ที่ไม่มีอคติ

ทั้งสองสูตรวัดความแปรปรวนโดยคำนวณรากที่สองของค่าเฉลี่ยของความเบียงเบนกำลังสองจาก Mean Variance ซึ่งเป็นค่ากำลังสองของ Standard Deviation ให้มาตรวัดการกระจายทางเลือกที่ใช้กันอย่างแพร่หลายในการวิเคราะห์ความเชื่อมั่น เช่น Cronbach's Alpha และการประเมินทางจิตมิติอื่นๆ

เอกสารอ้างอิง

Diez D.M., Cetinkaya-Rundel M., Barr C.D. (2019). OpenIntro: Statistics (4th Ed).

Field, A. (2018). Discovering statistics using IBM SPSS statistics (5th edition). Sage: Thousand Oaks, CA.