การเรียนรู้วิธีการวิเคราะห์ตัวแปรกำกับใน R (Moderation Analysis) เป็นทักษะที่สำคัญสำหรับการทำความเข้าใจความสัมพันธ์แบบมีเงื่อนไข (Conditional Relationships) ในข้อมูลวิจัยของคุณ คู่มือฉบับสมบูรณ์นี้จะสอนคุณวิธีการทำ Moderation Analysis โดยใช้ตัวแปรกำกับ (Moderating Variable) ตัวเดียว การแปลผล Moderating Effects การสร้าง Moderation Models และการตรวจสอบสมมติฐานด้วยตัวอย่างทีละขั้นตอนและข้อมูลจริง
บทความนี้จะช่วยให้คุณเข้าใจว่าตัวแปรกำกับเปลี่ยนแปลงความสัมพันธ์ระหว่างตัวแปรอย่างไร การทดสอบ Moderating Effects ใน Regression Models และวิธีการทำ Moderation Analysis ตั้งแต่การเตรียมข้อมูลจนถึงการรายงานผลลัพธ์ เราจะใช้ packages lmtest, car และ interactions เพื่อทำ Moderator Analysis แบบสมบูรณ์
คุณจะได้เรียนรู้พื้นฐาน Moderation ใน R วิธีการแปลผล Moderation Effects การประเมิน Moderation Model และการรายงานผลลัพธ์ตามมาตรฐาน APA รวมถึงการทดสอบสมมติฐาน การสร้างกราพแสดง Interaction Effects และการเข้าใจว่าเมื่อใดตัวแปรกำกับมีอิทธิพลอย่างมีนัยสำคัญต่อผลลัพธ์การวิจัยของคุณ
อย่างไรก็ตาม หากคุณต้องการวิเคราะห์ตัวแปรกำกับหลายตัว (Multiple Moderators) แนะนำให้อ่านคู่มือของเราเรื่อง How To Run Multiple Moderation Analyses in R
Moderation Analysis คืออะไร?
Moderation Analysis เป็นวิธีการวิเคราะห์ทางสถิติที่ใช้กันอย่างแพร่หลายในงานวิจัยเพื่อตรวจสอบผลกระทบตามเงื่อนไข (Conditional Effects) ของตัวแปรอิสระที่มีต่อตัวแปรตาม กล่าวง่ายๆ คือ การประเมินว่าตัวแปรที่สาม (ตัวแปรกำกับ หรือ Moderator) เปลี่ยนแปลงความสัมพันธ์ระหว่างสาเหตุ (ตัวแปรอิสระ) และผลลัพธ์ (ตัวแปรตาม) อย่างไร
ในภาษาทางสถิติ ความสัมพันธ์นี้สามารถอธิบายได้ด้วยสมการ Moderated Multiple Regression:
โดยที่:
- Y แทนตัวแปรตาม (Dependent Variable)
- X คือตัวแปรอิสระ (Independent Variable)
- Z แทนตัวแปรกำกับ (Moderator Variable)
- β₀, β₁, β₂ และ β₃ คือค่าสัมประสิทธิ์ที่แทน Intercept, ผลกระทบของตัวแปรอิสระ, ผลกระทบของตัวแปรกำกับ และผลกระทบปฏิสัมพันธ์ (Interaction Effect) ระหว่างตัวแปรอิสระและตัวแปรกำกับตามลำดับ
- ε คือ Error Term
ใน Moderation Analysis ส่วนประกอบหลักคือ Interaction Term (β₃*XZ) หากค่าสัมประสิทธิ์ β₃ มีนัยสำคัญทางสถิติ (p-value < 0.05) แสดงว่ามี Moderation Effect
คุณค่าของ Moderation Analysis อยู่ที่ความสามารถในการเปิดเผยความสัมพันธ์แบบมีเงื่อนไข แทนที่จะถามว่า "X มีผลต่อ Y หรือไม่?" เราถามว่า "ความสัมพันธ์ X→Y ขึ้นอยู่กับ Z หรือไม่?" สิ่งนี้ช่วยให้เราเข้าใจว่าภายใต้เงื่อนไขใด หรือ สำหรับใคร ผลกระทบเกิดขึ้น
สมมติฐานของ Moderation Analysis
มีสมมติฐานหลายประการที่ต้องเป็นไปตามเมื่อทำ Moderation Analysis สมมติฐานเหล่านี้คล้ายกับสมมติฐานของ Multiple Linear Regression เนื่องจาก Moderation Analysis โดยทั่วไปเกี่ยวข้องกับ Multiple Regression ที่มี Interaction Term นี่คือสมมติฐานหลัก:
-
Linearity (ความเป็นเส้นตรง): ความสัมพันธ์ระหว่าง Predictor แต่ละตัว (ตัวแปรอิสระและตัวแปรกำกับ) กับผลลัพธ์ (ตัวแปรตาม) เป็นเชิงเส้น สมมติฐานนี้สามารถตรวจสอบได้ด้วยภาพโดยใช้ Scatter Plots ที่เราจะสร้างและอธิบายอย่างละเอียดในบทความนี้
-
Independence of observations (ความเป็นอิสระของข้อมูล): สันนิษฐานว่าข้อมูลแต่ละตัวเป็นอิสระจากกัน นี่เป็นประเด็นเรื่องการออกแบบการศึกษามากกว่าสิ่งที่สามารถทดสอบได้ หากข้อมูลของคุณเป็น Time Series หรือ Clustered Data สมมติฐานนี้อาจถูกละเมิด
-
Homoscedasticity (ความแปรปรวนคงที่): สมมติฐานว่าความแปรปรวนของความคลาดเคลื่อนคงที่ในทุกระดับของตัวแปรอิสระ กล่าวอีกนัยหนึ่ง การกระจายของ Residuals ควรเท่ากันโดยประมาณในทุกค่าที่ทำนาย สามารถตรวจสอบได้โดยดูกราฟของ Residuals เทียบกับค่าที่ทำนาย
-
Normality of residuals (การแจกแจงปกติของ Residuals): สันนิษฐานว่า Residuals (ความคลาดเคลื่อน) มีการแจกแจงแบบปกติ สามารถตรวจสอบได้โดยใช้ Q-Q Plot
-
No multicollinearity (ไม่มีปัญหา Multicollinearity): ตัวแปรอิสระและตัวแปรกำกับไม่ควรมีความสัมพันธ์กันสูงมาก ความสัมพันธ์สูง (Multicollinearity) สามารถทำให้ความแปรปรวนของค่าสัมประสิทธิ์ Regression เพิ่มขึ้นและทำให้การประมาณค่าไวต่อการเปลี่ยนแปลงเล็กน้อยในโมเดล Variance Inflation Factor (VIF) มักใช้ตรวจสอบ Multicollinearity
-
No influential cases (ไม่มีข้อมูลที่มีอิทธิพลมากเกินไป): การวิเคราะห์ไม่ควรได้รับอิทธิพลมากเกินไปจากข้อมูลตัวใดตัวหนึ่ง Cook's Distance สามารถใช้ตรวจสอบข้อมูลที่มีอิทธิพลซึ่งอาจมีผลต่อการประมาณค่าสัมประสิทธิ์ Regression มากเกินไป
การกำหนด Moderation Analysis Model
สมมติว่าเรากำลังมองหาคำตอบสำหรับคำถามวิจัยต่อไปนี้:
"ความสัมพันธ์ระหว่างการดื่มกาแฟ (วัดจากจำนวนถ้วยที่ดื่ม) กับผลผลิตของพนักงานแตกต่างกันอย่างไรตามความทนทานต่อคาเฟอีนของแต่ละบุคคล?"
ดังนั้นเราสามารถกำหนดสมมติฐานดังนี้:
"ระดับความทนทานต่อคาเฟอีนของบุคคลกำกับความสัมพันธ์ระหว่างการดื่มกาแฟและผลผลิต"
สิ่งที่เรากำลังพยายามตอบด้วยสมมติฐานนี้คือ ผลกระทบของการดื่มกาแฟต่อผลผลิตเหมือนกันสำหรับทุกคนหรือไม่ หรือเปลี่ยนแปลงตามความทนทานต่อคาเฟอีน กล่าวอีกนัยหนึ่ง เรากำลังสำรวจว่าประโยชน์ด้านผลผลิต (หรือข้อเสีย) ของกาแฟเหมือนกันสำหรับทุกคนหรือไม่ หรือแตกต่างกันตามความทนทานต่อคาเฟอีนของแต่ละคน
ดังนั้น การศึกษาของเราประกอบด้วยตัวแปรต่อไปนี้: การดื่มกาแฟ (ตัวแปรอิสระ), ผลผลิต (ตัวแปรตาม) และ ความทนทานต่อคาเฟอีน (ตัวแปรกำกับ)
แผนภาพต่อไปนี้อธิบายประเภทของตัวแปรในการศึกษาของเราและความสัมพันธ์ระหว่างตัวแปรในบริบทของ Moderation Analysis:
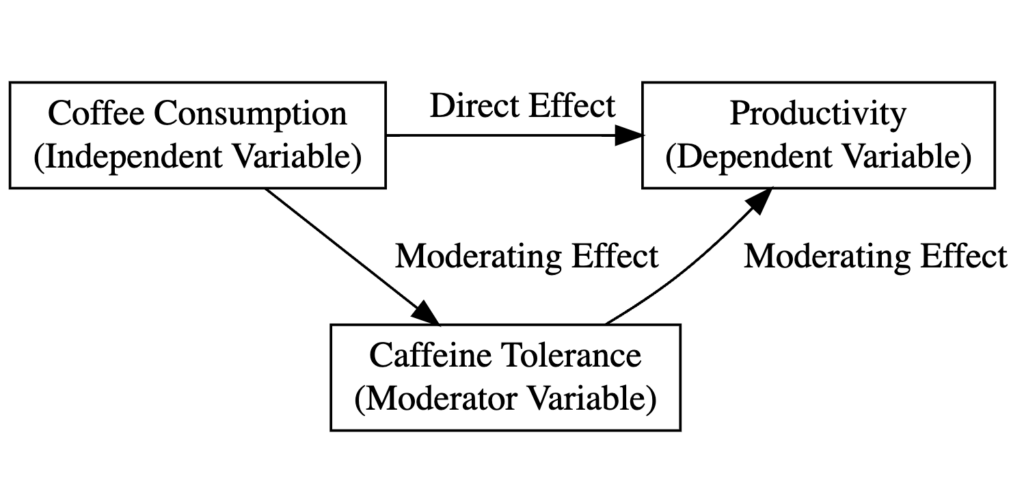 แผนภาพ Moderation Analysis Model แสดงความสัมพันธ์ระหว่างการดื่มกาแฟ (X), ผลผลิต (Y) และความทนทานต่อคาเฟอีน (Moderator)
แผนภาพ Moderation Analysis Model แสดงความสัมพันธ์ระหว่างการดื่มกาแฟ (X), ผลผลิต (Y) และความทนทานต่อคาเฟอีน (Moderator)
โดยที่:
- การดื่มกาแฟ (Cups) คือตัวแปรอิสระ
- ผลผลิตของพนักงาน (Productivity) คือตัวแปรตาม
- ความทนทานต่อคาเฟอีนของแต่ละบุคคล (Tolerance) คือตัวแปรกำกับ
- Direct Effect แสดงว่าการดื่มกาแฟมีผลต่อผลผลิตโดยรวมอย่างไร
- Moderating Effect (Interaction) แสดงว่าความสัมพันธ์นี้แตกต่างกันหรือไม่ตามระดับความทนทานต่อคาเฟอีน หากมีนัยสำคัญ หมายความว่าความสัมพันธ์กาแฟ-ผลผลิตแข็งแกร่งกว่า (หรืออ่อนแอกว่า) สำหรับคนที่มีความทนทานต่อคาเฟอีนสูงเมื่อเทียบกับต่ำ
วิธีการทำ Moderation Analysis ใน R
ตอนนี้เราได้ครอบคลุมพื้นฐานทฤษฎีเพียงพอแล้ว ถึงเวลาเริ่มเรียนรู้วิธีการทำ Moderation Analysis ใน R เราหวังว่าคุณมี R/R Studio ติดตั้งและพร้อมใช้งานแล้ว แต่ถ้ายังไม่มี นี่คือคู่มือสั้นๆ เรื่อง how to install R and R Studio บนคอมพิวเตอร์ของคุณ
เราจะใช้ตัวอย่าง "กาแฟ" ที่กล่าวถึงก่อนหน้านี้ จำได้ว่าเราตั้งสมมติฐานว่า ระดับความทนทานต่อคาเฟอีนของบุคคลกำกับความสัมพันธ์ระหว่างการดื่มกาแฟและผลผลิต
ขั้นตอนที่ 1: ติดตั้งและโหลด Packages ที่จำเป็นใน R
R มี Packages มากมายที่ช่วยในการทำ Moderation Analysis ในกรณีของเรา เราจะใช้สี่ packages ได้แก่: lmtest, car, interactions และ ggplot2 นี่คือคำอธิบายของแต่ละ Package และวัตถุประสงค์:
-
lmtest: Package
lmtestให้เครื่องมือสำหรับการตรวจสอบวินิจฉัยใน Linear Regression Models ซึ่งจำเป็นสำหรับการตรวจสอบว่าโมเดลของเราเป็นไปตามสมมติฐานหลักหรือไม่ Package นี้สามารถทำ Wald, F และ Likelihood Ratio Tests ในบริบทของ Moderation Analysis คุณอาจใช้lmtestเพื่อตรวจสอบ Heteroscedasticity (ความแปรปรวนที่ไม่คงที่) เป็นต้น -
car: Package
car(Companion to Applied Regression) เป็นอีกหนึ่งเครื่องมือสำหรับการวินิจฉัย Regression และรวมถึงฟังก์ชันสำหรับคำนวณ Variance Inflation Factor (VIF) ซึ่งช่วยตรวจจับปัญหา Multicollinearity (เมื่อตัวแปรอิสระมีความสัมพันธ์กันสูง) Multicollinearity อาจทำให้เกิดปัญหาในการประมาณค่าสัมประสิทธิ์ Regression และ Standard Errors -
interactions: Package
interactionsใช้สำหรับสร้างภาพและวิเคราะห์ Simple Slope ของ Interaction Terms ใน Regression Models สามารถสร้างกราฟประเภทต่างๆ เพื่อช่วยแสดง Moderation Effect และแสดงว่าความสัมพันธ์ระหว่างตัวแปรอิสระและตัวแปรตามเปลี่ยนแปลงอย่างไรในระดับต่างๆ ของตัวแปรกำกับ -
ggplot2:
ggplot2เป็นหนึ่งใน Packages ที่ได้รับความนิยมมากที่สุดสำหรับการสร้างภาพข้อมูลใน R ใน Moderation Analysis,ggplot2สามารถใช้สร้าง Scatter Plots, Line Graphs และภาพอื่นๆ เพื่อช่วยให้คุณเข้าใจข้อมูลและความสัมพันธ์ระหว่างตัวแปรได้ดีขึ้น นอกจากนี้ยังช่วยในการแสดง Moderation Effect คือ แสดงว่าผลกระทบของตัวแปรอิสระต่อตัวแปรตามเปลี่ยนแปลงอย่างไรในระดับต่างๆ ของตัวแปรกำกับ
เราสามารถติดตั้ง Packages ที่แสดงด้านบนพร้อมกันได้โดยคัดลอกและวางคำสั่งต่อไปนี้ใน R Console:
install.packages("lmtest")
install.packages("car")
install.packages("interactions")
install.packages("ggplot2")เมื่อติดตั้งแล้ว โหลด Packages เข้าสู่ R Session:
library(lmtest)
library(car)
library(interactions)
library(ggplot2)ขั้นตอนที่ 2: นำเข้าข้อมูล
เพื่อให้ง่ายต่อการเรียนรู้วิธีการทำ Moderation Analysis ใน R คุณสามารถดาวน์โหลดชุดข้อมูลฝึกหัดจาก Sidebar - ชุดข้อมูลตัวอย่างของผู้ตอบแบบสอบถาม 30 คนที่มีคะแนนสำหรับตัวแปรในการศึกษาของเรา: การดื่มกาแฟ (Cups), ความทนทานต่อคาเฟอีน (Tolerance) และผลผลิต (Productivity)
- เรียนรู้ how to import Excel .xls or .xlsx file formats into R
- เรียนรู้ how to import a CSV file in R
หากชุดข้อมูลของคุณไม่ใหญ่เกินไป คุณสามารถป้อนข้อมูลด้วยตัวเองใน R ในรูปแบบของ Data Frame ดังนี้:
data <- data.frame(
Respondent = 1:30,
Cups = c(2, 4, 1, 3, 2, 3, 1, 2, 2, 4, 2, 3, 1, 3, 3, 2, 2, 4, 1, 3, 2, 3, 1, 2, 2, 4, 2, 3, 1, 3),
Tolerance = c(7, 5, 6, 7, 8, 6, 7, 7, 6, 8, 7, 7, 6, 7, 8, 6, 7, 5, 6, 7, 8, 6, 7, 7, 6, 8, 7, 7, 6, 7),
Productivity = c(5, 6, 4, 6, 7, 7, 4, 6, 5, 7, 5, 6, 4, 6, 7, 5, 5, 6, 4, 6, 7, 7, 4, 6, 5, 7, 5, 6, 4, 6)
)สำคัญ: ชุดข้อมูลนี้ใช้เพื่อการศึกษาเท่านั้น เนื่องจากมีค่าแบบสุ่มและอาจไม่สะท้อนสถานการณ์จริง "Cups" (ตัวแปรอิสระ) สะท้อนจำนวนถ้วยกาแฟที่ดื่มต่อวัน "Tolerance" (ตัวแปรกำกับ) เป็นคะแนนจาก 10 ที่สะท้อนความทนทานต่อคาเฟอีนของแต่ละบุคคล และ "Productivity" (ตัวแปรตาม) เป็นคะแนนจาก 10 ที่บ่งชี้ระดับผลผลิตของบุคคล
ขั้นตอนที่ 3: สร้าง Moderated Multiple Regression Model
ในการสร้าง Moderated Multiple Regression Model เราจะใช้ฟังก์ชัน lm() ใน R โปรดทราบว่า data คือ Data Frame ของเรา และ Cups, Tolerance และ Productivity เป็นคอลัมน์ใน Data Frame นั้น
model <- lm(Productivity ~ Cups*Tolerance, data)
summary(model)คำสั่งนี้จะแสดงผลลัพธ์สรุปของโมเดล รวมถึงการวิเคราะห์โดยละเอียดของความเหมาะสมของโมเดลและนัยสำคัญของแต่ละเทอมในโมเดลดังที่เห็นในภาพด้านล่าง:
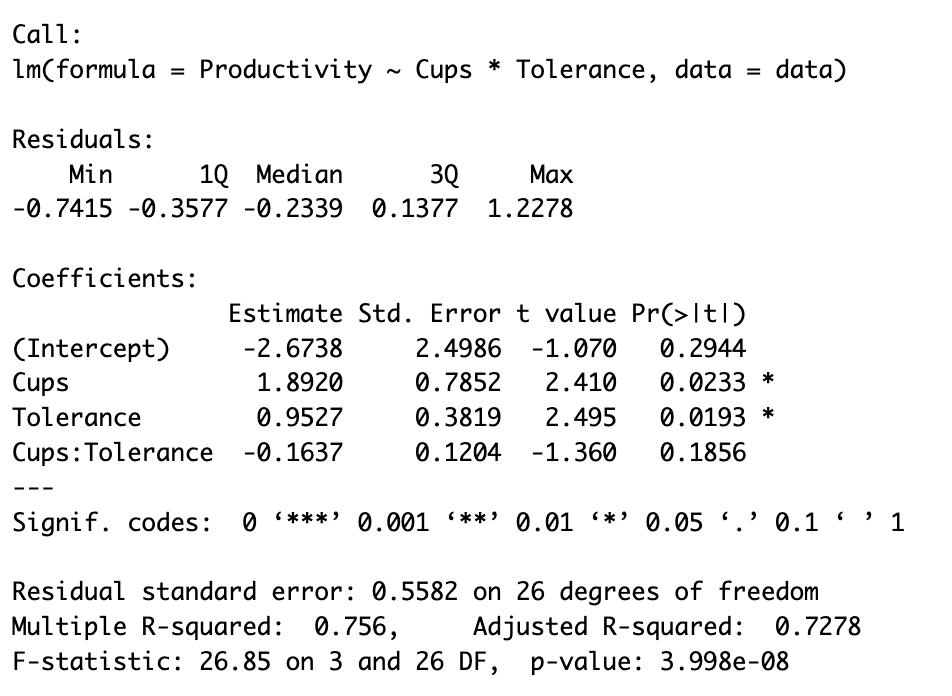 ผลลัพธ์ R แสดง Moderated Multiple Regression พร้อม Interaction Term (Cups:Tolerance) และระดับนัยสำคัญ
ผลลัพธ์ R แสดง Moderated Multiple Regression พร้อม Interaction Term (Cups:Tolerance) และระดับนัยสำคัญ
ขั้นตอนที่ 4: การแปลผล Moderation Effect
ผลลัพธ์ lm() ให้ข้อมูลสำคัญสำหรับการแปลผล Moderation เน้นที่ค่าสัมประสิทธิ์เหล่านี้:
- Cups: ผลกระทบเชิงบวก (1.8920, p < 0.05) - การดื่มกาแฟเพิ่มผลผลิต
- Tolerance: ผลกระทบเชิงบวก (0.9527, p < 0.05) - ความทนทานต่อคาเฟอีนที่สูงขึ้นเพิ่มผลผลิต
- Cups:Tolerance: Interaction Term (-0.1637, p > 0.05) - ไม่มีนัยสำคัญทางสถิติ
เนื่องจาก P-value ของ Interaction มากกว่า 0.05 เราสรุปว่า ไม่มี Moderation Effect ที่มีนัยสำคัญ ความสัมพันธ์ระหว่างกาแฟและผลผลิตไม่ได้ขึ้นอยู่กับความทนทานต่อคาเฟอีนอย่างมีความหมายในตัวอย่างนี้
ประสิทธิภาพของโมเดล:
- R² = 0.756: โมเดลอธิบายความแปรปรวนของผลผลิต 75.6%
- Adjusted R² = 0.728: ยังคงสูงหลังจากปรับสำหรับ Predictors
- F-statistic (p < 0.001): โมเดลโดยรวมมีนัยสำคัญทางสถิติ
ขั้นตอนที่ 5: สร้างภาพแสดง Interaction Effect
เราสามารถสร้างกราฟเพื่อช่วยแสดง Interaction Effect ได้ง่ายๆ โดยใช้ฟังก์ชัน interact_plot ใน R ด้วยโค้ดต่อไปนี้:
interactions::interact_plot(model, pred = Cups, modx = Tolerance)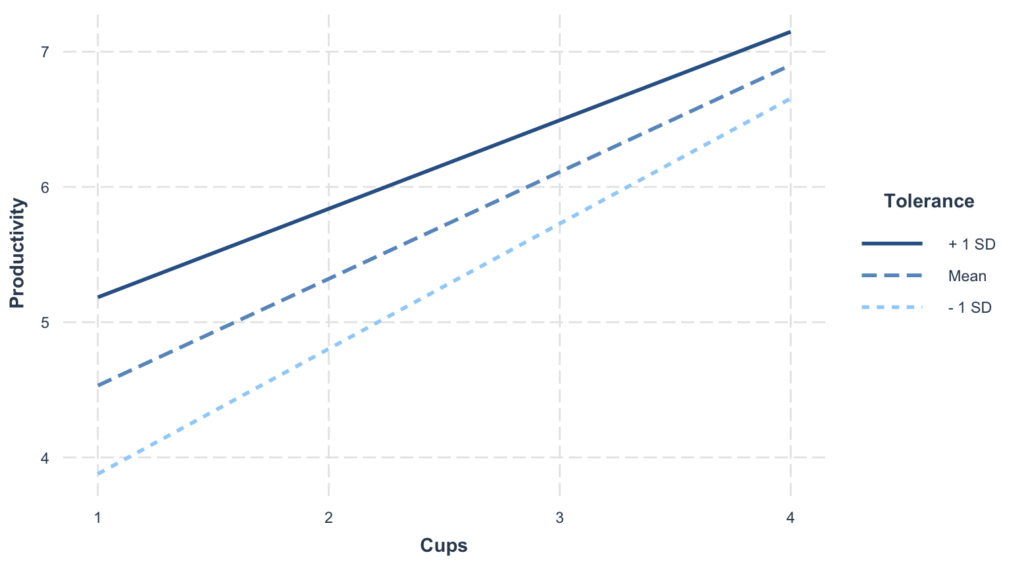 Interaction Plot แสดง Moderating Effect ของความทนทานต่อคาเฟอีนต่อความสัมพันธ์ระหว่างการดื่มกาแฟและผลผลิต
Interaction Plot แสดง Moderating Effect ของความทนทานต่อคาเฟอีนต่อความสัมพันธ์ระหว่างการดื่มกาแฟและผลผลิต
กราฟนี้แสดงว่าความสัมพันธ์กาแฟ-ผลผลิตเปลี่ยนแปลงอย่างไรในระดับความทนทานต่างๆ แต่ละเส้นแทนระดับต่างๆ ของตัวแปรกำกับ (ความทนทานต่ำ, ปานกลาง, สูง)
การแปลผลสำคัญ:
- เส้นไม่ขนานกัน = มี Moderation (ผลกระทบของกาแฟขึ้นอยู่กับความทนทาน)
- เส้นขนานกัน = ไม่มี Moderation (ผลกระทบของกาแฟเหมือนกันไม่ว่าความทนทานจะเป็นอย่างไร)
- Confidence Bands แสดงความไม่แน่นอนรอบแต่ละความชัน
ขั้นตอนที่ 6: ตรวจสอบสมมติฐานและการวินิจฉัยโมเดล
ก่อนที่จะเชื่อผลลัพธ์ของเรา เราต้องตรวจสอบสมมติฐาน Regression: Linearity, Independence, Homoscedasticity, Normality และการไม่มี Multicollinearity เราจะตรวจสอบ Outliers และข้อมูลที่มีอิทธิพลซึ่งอาจบิดเบือนผลการค้นพบของเราด้วย
1. Linearity & Additivity (ความเป็นเส้นตรงและการบวกรวม)
วาดกราฟ Residuals เทียบกับค่าที่ทำนาย การกระจายแบบสุ่มรอบศูนย์บ่งชี้ว่าเป็นไปตามสมมติฐาน Linearity
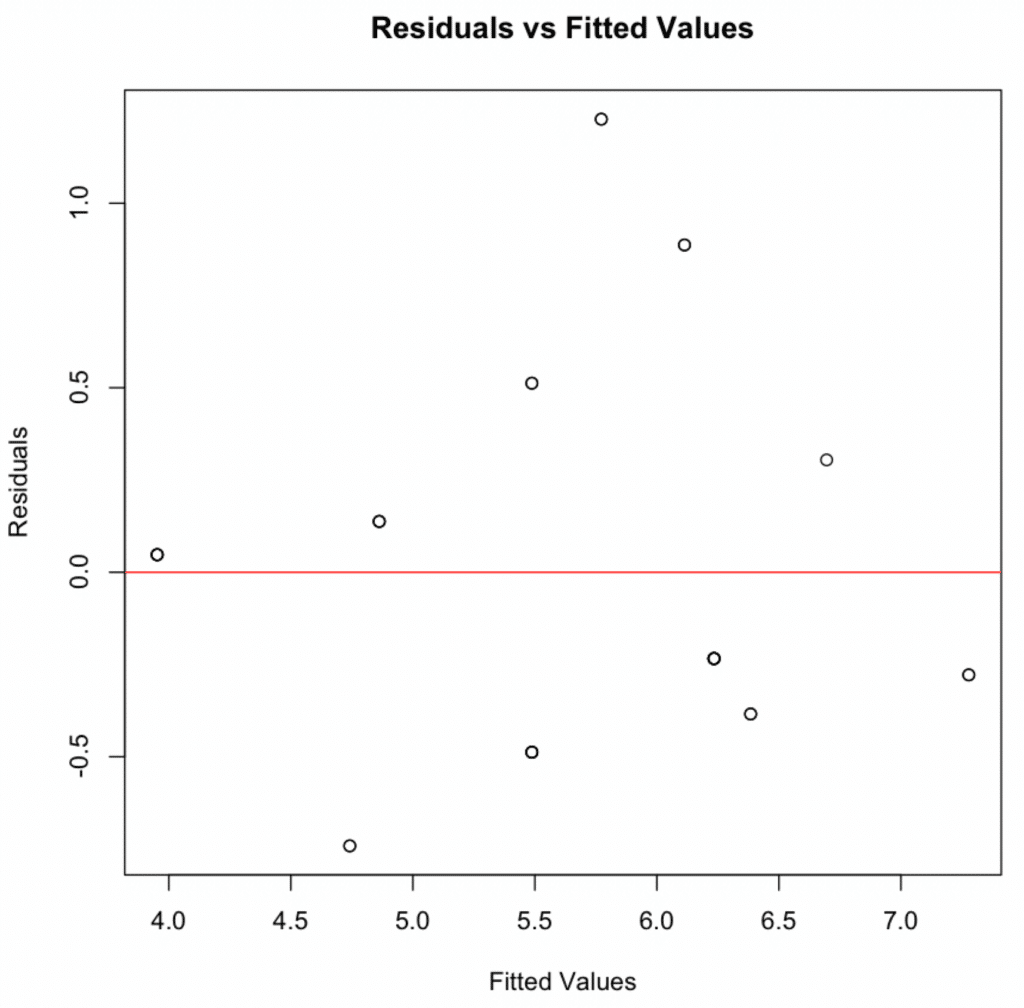 กราฟ Residuals vs Fitted Values แสดงว่าเป็นไปตามสมมติฐาน Linearity ด้วยรูปแบบการกระจายแบบสุ่ม
กราฟ Residuals vs Fitted Values แสดงว่าเป็นไปตามสมมติฐาน Linearity ด้วยรูปแบบการกระจายแบบสุ่ม
2. Independence of Residuals (ความเป็นอิสระของ Residuals)
Durbin-Watson Test ตรวจจับ Autocorrelation ใน Residuals:
print(dwtest(model))Durbin-Watson = 1.9833 (ใกล้ 2), p-value = 0.5468 → ไม่มี Autocorrelation เป็นไปตามสมมติฐาน Independence
 ผลลัพธ์ Durbin-Watson Test แสดง DW = 1.9833 ยืนยันสมมติฐานความเป็นอิสระของ Residuals
ผลลัพธ์ Durbin-Watson Test แสดง DW = 1.9833 ยืนยันสมมติฐานความเป็นอิสระของ Residuals
3. Homoscedasticity (ความแปรปรวนคงที่)
ตรวจสอบความแปรปรวนที่เท่ากันของ Residuals ในทุกค่าที่ทำนาย:
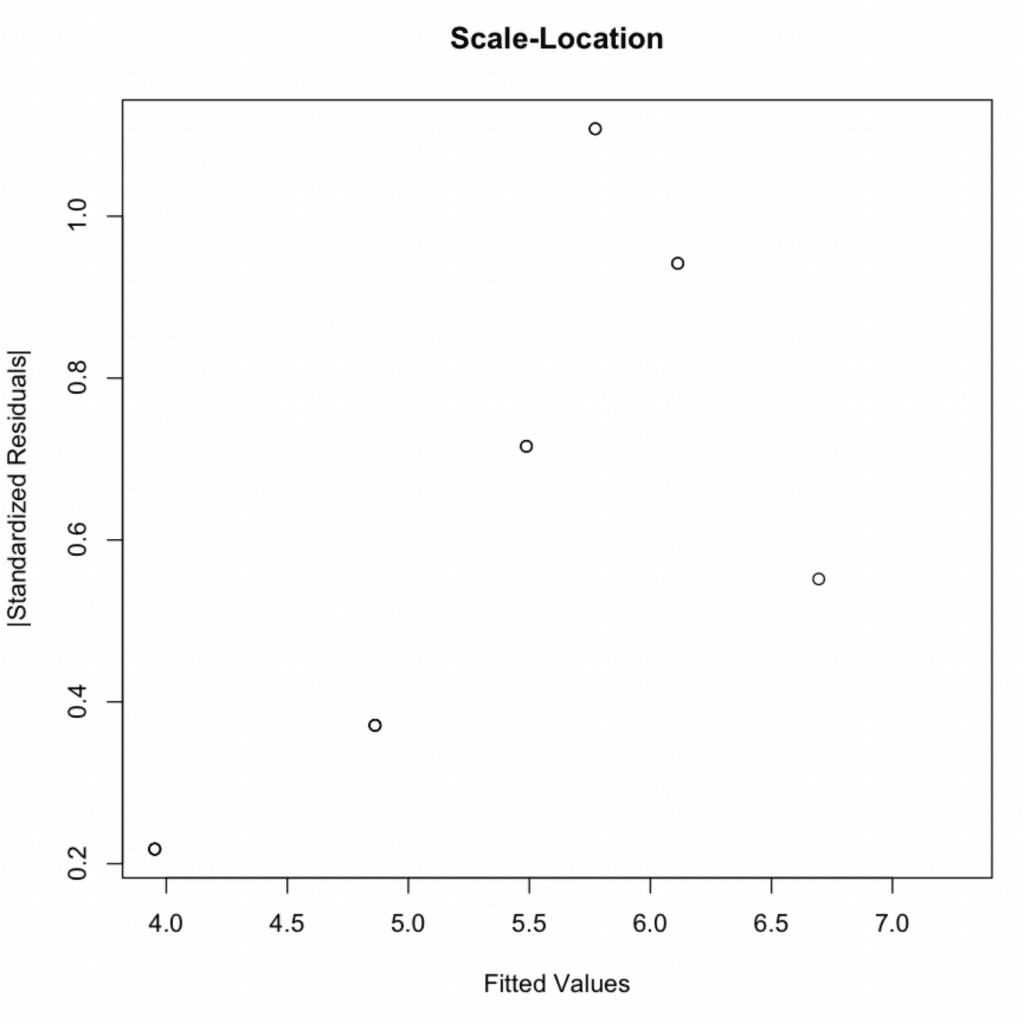 กราฟ Scale-Location แสดง Homoscedasticity ด้วยความแปรปรวนคงที่ในทุกค่าที่ทำนาย
กราฟ Scale-Location แสดง Homoscedasticity ด้วยความแปรปรวนคงที่ในทุกค่าที่ทำนาย
ยืนยันด้วย Breusch-Pagan Test:
print(bptest(model)) ผลลัพธ์ Breusch-Pagan Test ด้วย p-value = 0.2488 ยืนยันสมมติฐานความแปรปรวนเท่ากัน
ผลลัพธ์ Breusch-Pagan Test ด้วย p-value = 0.2488 ยืนยันสมมติฐานความแปรปรวนเท่ากัน
P-value = 0.2488 > 0.05 → เป็นไปตามสมมติฐาน Homoscedasticity
4. Normality of Residuals (การแจกแจงปกติของ Residuals)
ใช้ Q-Q Plot เพื่อตรวจสอบว่า Residuals มีการแจกแจงแบบปกติหรือไม่ จุดควรอยู่ตามเส้นทแยงมุม
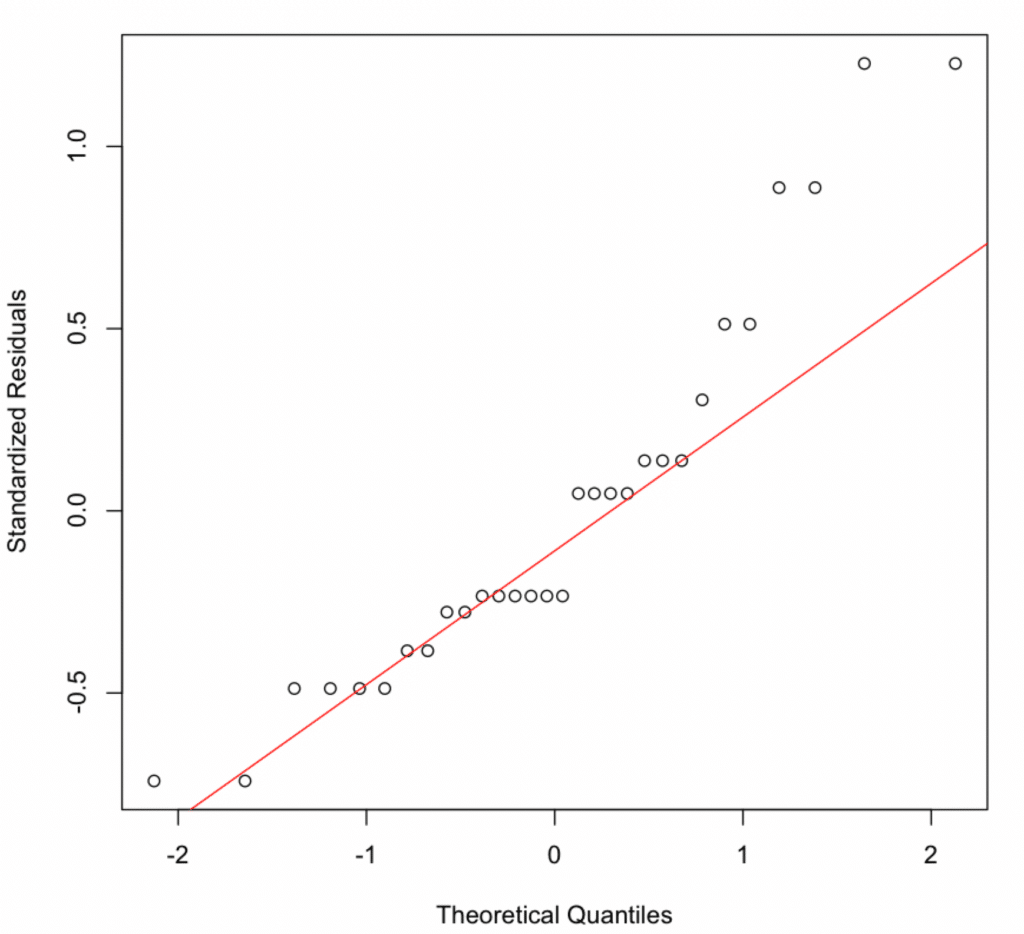 Normal Q-Q Plot แสดง Residuals ตามเส้นทแยงมุมบางส่วนมีการเบี่ยงเบนเล็กน้อยที่หาง
Normal Q-Q Plot แสดง Residuals ตามเส้นทแยงมุมบางส่วนมีการเบี่ยงเบนเล็กน้อยที่หาง
Q-Q Plot แสดงการเบี่ยงเบนเล็กน้อย ยืนยันด้วย Shapiro-Wilk Test:
shapiro.test(resid(model)) ผลลัพธ์ Shapiro-Wilk Test แสดง p-value = 0.0088 บ่งชี้การเบี่ยงเบนเล็กน้อยจากการแจกแจงปกติสมบูรณ์
ผลลัพธ์ Shapiro-Wilk Test แสดง p-value = 0.0088 บ่งชี้การเบี่ยงเบนเล็กน้อยจากการแจกแจงปกติสมบูรณ์
P-value = 0.0088 < 0.05 บ่งชี้ว่า Residuals ไม่มีการแจกแจงปกติอย่างสมบูรณ์แบบ อย่างไรก็ตาม ด้วยตัวอย่างขนาดเล็ก (n=30) การทดสอบนี้ไวต่อการเบี่ยงเบนเล็กน้อยมาก Q-Q Plot แสดงการเบี่ยงเบนเพียงเล็กน้อย และ Regression มีความทนทานต่อการละเมิดความเป็นปกติปานกลางเนื่องจาก Central Limit Theorem
5. Multicollinearity
ตรวจสอบ Multicollinearity โดยใช้ Variance Inflation Factor (VIF) VIF > 10 บ่งชี้ Multicollinearity สูง
print(vif(model)) ผลลัพธ์ VIF แสดง Multicollinearity สูงตามที่คาดไว้เนื่องจาก Interaction Term ใน Moderation Analysis
ผลลัพธ์ VIF แสดง Multicollinearity สูงตามที่คาดไว้เนื่องจาก Interaction Term ใน Moderation Analysis
ค่า VIF: Cups = 53.36, Tolerance = 9.30, Cups:Tolerance = 65.12 ค่าสูงเหล่านี้คาดหวังและยอมรับได้ ใน Moderation Analysis Interaction Terms ตามคำนิยามมีความสัมพันธ์กับตัวแปรองค์ประกอบของพวกมัน เพื่อลด VIF ให้ทำ Center ตัวแปรก่อนสร้าง Interaction Term (ลบค่าเฉลี่ยออกจากแต่ละค่า)
6. Outliers and Influential Observations (Outliers และข้อมูลที่มีอิทธิพล)
ตรวจจับ Outliers โดยใช้ Bonferroni Outlier Test:
print(outlierTest(model)) ผลลัพธ์ Bonferroni Outlier Test บ่งชี้ว่าไม่มี Outliers ที่มีนัยสำคัญทางสถิติหลังการแก้ไขการทดสอบหลายครั้ง
ผลลัพธ์ Bonferroni Outlier Test บ่งชี้ว่าไม่มี Outliers ที่มีนัยสำคัญทางสถิติหลังการแก้ไขการทดสอบหลายครั้ง
ข้อมูลที่ 6 มี Residual ที่ใหญ่ที่สุด (2.517) แต่ Bonferroni p-value = 0.559 > 0.05 → ไม่ตรวจพบ Outliers ที่มีนัยสำคัญ
ตรวจสอบข้อมูลที่มีอิทธิพลโดยใช้ Cook's Distance:
# Influential observations
influence <- influence.measures(model)
# Print Cook's distance values for each observation
print(influence$is.inf)
# Plot Cook's distance
plot(influence$infmat[, "cook.d"],
main = "Cook's distance plot",
ylab = "Cook's distance",
ylim = c(0, max(1, max(influence$infmat[, "cook.d"]))))
# Add a reference line for Cook's distance = 1
abline(h = 1, col = "red")Cook's Distance ที่มากกว่า 1 บ่งชี้ข้อมูลที่มีอิทธิพลสูง
 ค่า Cook's Distance Influence Measures สำหรับ Moderation Analysis ใน R
ค่า Cook's Distance Influence Measures สำหรับ Moderation Analysis ใน R
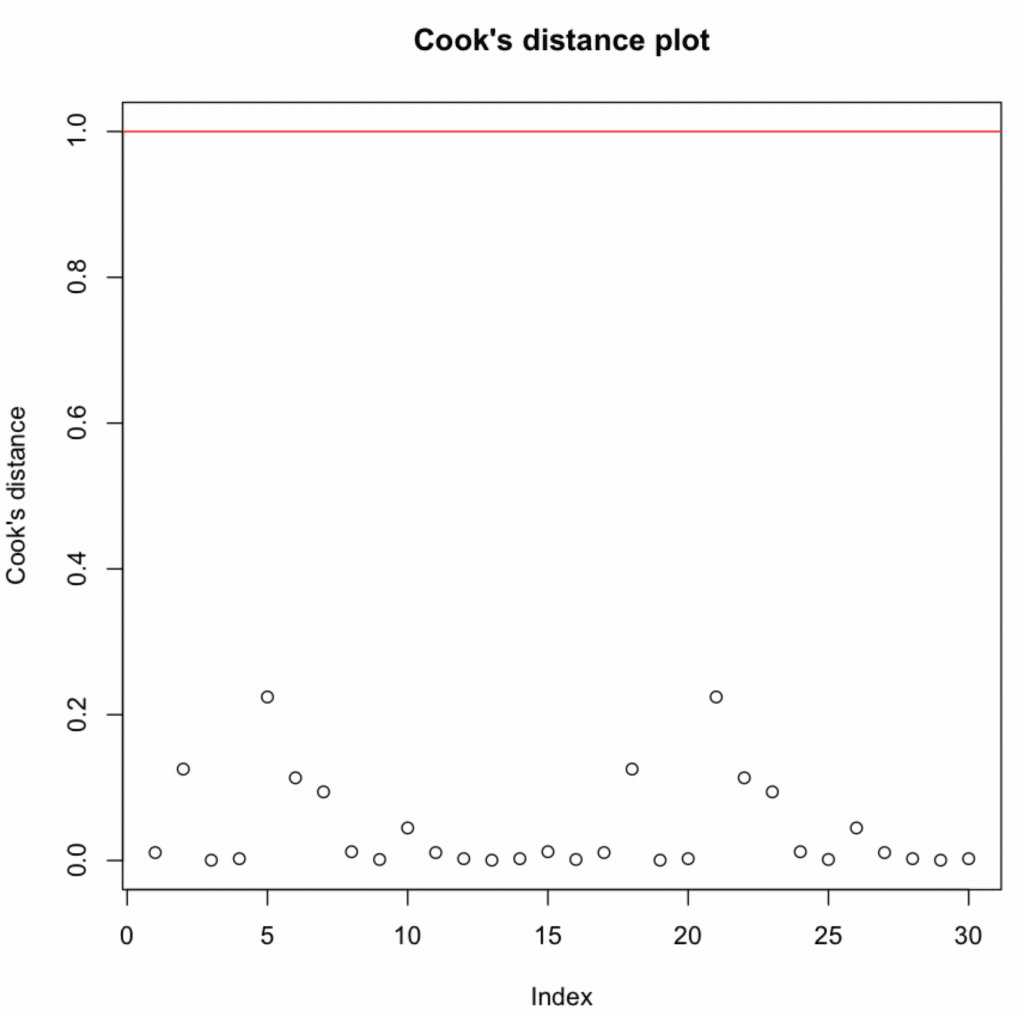 กราฟ Cook's Distance แสดงข้อมูลทั้งหมดต่ำกว่าเกณฑ์ 1
กราฟ Cook's Distance แสดงข้อมูลทั้งหมดต่ำกว่าเกณฑ์ 1
ค่าทั้งหมดต่ำกว่า 1 → ไม่ตรวจพบข้อมูลที่มีอิทธิพล
Export Diagnostic Plots เป็น PDF:
# Fit the model
model <- lm(Productivity ~ Cups*Tolerance, data = data)
# Diagnostic Plots
par(mfrow = c(2, 2), oma = c(0, 0, 2, 0))
plot(model, las = 1)
mtext("Diagnostic Plots", outer = TRUE, line = -1, cex = 1.5)
# Save the plots as a PDF file
pdf("Diagnostic_Plots.pdf")
par(mfrow = c(2, 2), oma = c(0, 0, 2, 0))
plot(model, las = 1)
mtext("Diagnostic Plots", outer = TRUE, line = -1, cex = 1.5)
dev.off()Script ด้านบนสร้างโมเดล สร้าง Diagnostic Plots สี่แบบที่เกี่ยวข้อง จากนั้นบันทึกเป็นไฟล์ PDF ชื่อ "Diagnostic_Plots.pdf" Diagnostic Plots เหล่านี้ช่วยตรวจสอบสมมติฐานของ Linearity, Independence, Homoscedasticity และการไม่มีข้อมูลที่มีอิทธิพลตามลำดับ
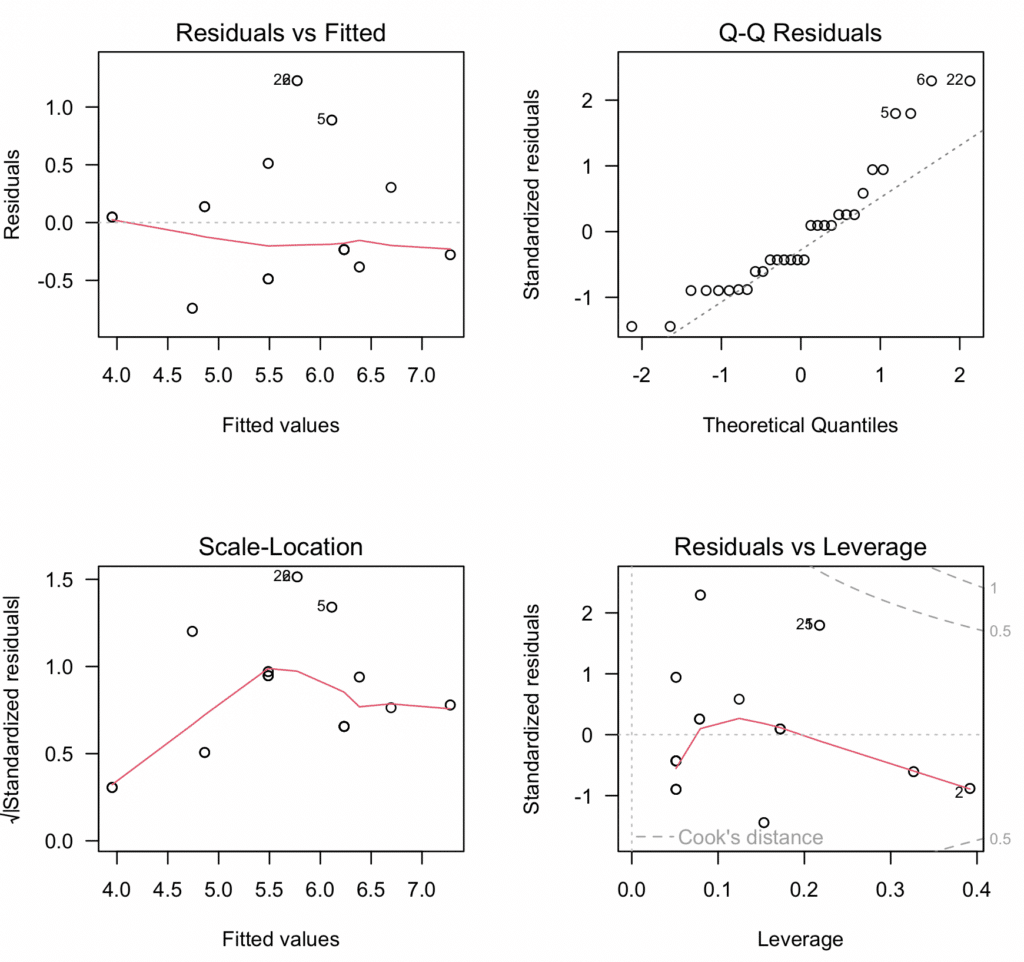 Diagnostic Plot สี่แผงสำหรับ Moderation Analysis แสดงการทดสอบสมมติฐานทั้งหมดในภาพเดียว
Diagnostic Plot สี่แผงสำหรับ Moderation Analysis แสดงการทดสอบสมมติฐานทั้งหมดในภาพเดียว
ขั้นตอนที่ 7: การรายงานผลลัพธ์
สุดท้าย ถึงเวลาสรุปการค้นพบและรายงานผลลัพธ์ของ Moderation Analysis ที่เราทำใน R ดังนี้:
ใน Moderation Analysis ใน R ของเรา เรามีจุดมุ่งหมายเพื่อศึกษาผลกระทบของการดื่มคาเฟอีน (วัดจากจำนวนถ้วยกาแฟที่ดื่ม) และความทนทานต่อความเครียดต่อผลผลิต พร้อมทั้งพิจารณา Moderating Effect ที่อาจเกิดขึ้นของความทนทานต่อความเครียดต่อความสัมพันธ์ระหว่างการดื่มคาเฟอีนและผลผลิต บรรลุผลผ่าน Multiple Regression Model ที่ระบุด้วย Interaction Term สำหรับถ้วยกาแฟและความทนทานต่อความเครียด
โมเดลที่สร้างขึ้นให้ข้อมูลเชิงลึกที่มีค่าเกี่ยวกับความสัมพันธ์ที่ตั้งสมมติฐานไว้ Interaction Term (Cups*Tolerance) ไม่มีนัยสำคัญทางสถิติ (p > 0.05) แสดงว่าไม่มี Moderation Effect ที่มีนัยสำคัญของความทนทานต่อคาเฟอีนต่อความสัมพันธ์ระหว่างการดื่มกาแฟและผลผลิตในตัวอย่างนี้ สิ่งนี้บ่งชี้ว่าผลกระทบของกาแฟต่อผลผลิตไม่แตกต่างกันอย่างมีนัยสำคัญตามระดับความทนทานต่อคาเฟอีนของบุคคล อย่างน้อยก็ไม่ใช่ในชุดข้อมูลนี้
การวิเคราะห์เพิ่มเติมของสมมติฐานและการวินิจฉัยโมเดลเปิดเผยว่าโมเดลเหมาะสมกับข้อมูลของเรา:
-
Linearity & Additivity: กราฟ Residuals vs Fitted Values บ่งชี้ว่าความสัมพันธ์เป็นเชิงเส้นและการบวกรวม โดยไม่มีรูปแบบที่เห็นได้ชัดหรือการเบี่ยงเบนจากค่าเฉลี่ยศูนย์
-
Independence of Residuals: Durbin-Watson Test ให้ค่าสถิติ 1.9833 (p-value = 0.5468) บ่งชี้ว่าไม่มีหลักฐานของ Autocorrelation ใน Residuals
-
Homoscedasticity: กราฟ Scale-Location และ Breusch-Pagan Test (p-value = 0.2488) ยืนยันสมมติฐานของความแปรปรวนเท่ากัน (Homoscedasticity) ของ Residuals
-
Normality of Residuals: Shapiro-Wilk Test บ่งชี้ว่า Residuals ไม่มีการแจกแจงปกติอย่างสมบูรณ์แบบ (p-value = 0.0088 < 0.05) อย่างไรก็ตาม เนื่องจากขนาดตัวอย่างเล็ก (n=30) การทดสอบนี้ไวต่อการเบี่ยงเบนเล็กน้อยมาก และ Q-Q Plot แสดงการเบี่ยงเบนเพียงเล็กน้อยจากความเป็นปกติ ด้วยตัวอย่างที่ใหญ่ขึ้น Regression Models มีความทนทานต่อการละเมิดความเป็นปกติปานกลางเนื่องจาก Central Limit Theorem
-
Multicollinearity: Variance Inflation Factors (VIFs) สำหรับ Predictors สูงกว่าเกณฑ์ทั่วไป 5 บ่งชี้การมีอยู่ของ Multicollinearity อย่างไรก็ตาม เนื่องจากคาดหวังสิ่งนี้เนื่องจากการรวม Interaction Terms สิ่งนี้ไม่ทำให้โมเดลของเราไม่ถูกต้อง
-
Outliers and Influential Observations: Bonferroni Outlier Test ไม่ตรวจพบ Outliers ที่มีนัยสำคัญ ค่า Cook's Distance ทั้งหมดต่ำกว่าเกณฑ์ 1 แสดงว่าไม่มีจุดที่มีอิทธิพลมากเกินไป
สรุปว่า Moderation Analysis ใน R ของเราไม่พบ Moderation Effect ที่มีนัยสำคัญทางสถิติของความทนทานต่อคาเฟอีนต่อความสัมพันธ์ระหว่างการดื่มกาแฟและผลผลิต แม้ว่าโมเดลจะอธิบายสัดส่วนความแปรปรวนที่สำคัญ (R² = 0.756) Interaction Term ก็ไม่มีนัยสำคัญ สิ่งนี้แสดงว่าในตัวอย่างนี้ ผลกระทบของกาแฟต่อผลผลิตไม่แตกต่างกันอย่างมีนัยสำคัญตามระดับความทนทานต่อคาเฟอีน การค้นพบเหล่านี้เน้นย้ำความสำคัญของขนาดตัวอย่างที่เพียงพอและความจำเป็นในการศึกษาซ้ำเพื่อตรวจจับ Moderation Effects อย่างน่าเชื่อถือ
สำคัญ: โปรดจำไว้ว่าต้องปรับการแปลผลให้เหมาะกับผลลัพธ์และบริบทจริงของคุณ นี่เป็นตัวอย่างทั่วไปและอาจไม่สอดคล้องอย่างสมบูรณ์กับเป้าหมายและผลลัพธ์การวิจัยเฉพาะของคุณ
คำถามที่พบบ่อย
สรุป
ในคู่มือฉบับสมบูรณ์นี้ คุณได้เรียนรู้วิธีการทำ Moderation Analysis ใน R ตั้งแต่ต้นจนจบ ตอนนี้คุณเข้าใจแล้วว่าตัวแปรกำกับคืออะไร วิธีการทดสอบ Moderating Effects การสร้างและประเมิน Moderation Models และการตรวจสอบสมมติฐาน Moderation Analysis ทั้งหมดโดยใช้การทดสอบวินิจฉัยและการสร้างภาพ
คุณได้เรียนรู้ทักษะที่จำเป็นสำหรับ Moderation ใน R: การสร้าง Interaction Terms, การแปลผล Moderation Effects, การใช้ฟังก์ชัน lm() สำหรับ Moderator Analysis และการสร้างภาพผลลัพธ์ด้วย Interaction Plots ไม่ว่าจะศึกษา ตัวแปรกำกับในงานวิจัยจิตวิทยา การวิเคราะห์ธุรกิจ หรือสังคมศาสตร์ ตอนนี้คุณสามารถทำ Moderation Analysis แบบสมบูรณ์และรายงานผลการค้นพบตามแนวทางปฏิบัติที่ดีที่สุดได้อย่างมั่นใจ
กรอบ Moderation Model ที่คุณได้เรียนรู้ - การทดสอบว่าตัวแปรกำกับมีอิทธิพลต่อความสัมพันธ์ระหว่าง Predictors และผลลัพธ์อย่างไร - เป็นพื้นฐานของการวิจัยทางสถิติขั้นสูง ด้วยความเข้าใจสมมติฐาน Moderation Analysis, การแปลผล Moderating Effects อย่างถูกต้อง และการรู้จักว่าเมื่อใดModeration มีอยู่ในข้อมูลของคุณ คุณพร้อมที่จะตอบคำถามวิจัยที่ซับซ้อนเช่น "สำหรับใคร" และ "ภายใต้เงื่อนไขใด"
จำไว้ว่า ชุดข้อมูลและคำถามวิจัยแต่ละชุดมีเอกลักษณ์เฉพาะ ดังนั้นปรับเทคนิค Moderation Analysis เหล่านี้ให้เหมาะกับความต้องการเฉพาะของคุณ Moderation ใน R เป็นเพียงหนึ่งในแนวทางการวิเคราะห์ที่ทรงพลัง - รวมกับวิธีการอื่นๆ เพื่อเปิดเผยเรื่องราวที่สมบูรณ์ในข้อมูลของคุณ
หากคุณพบว่าคู่มือ Moderation Analysis นี้มีข้อมูลที่เป็นประโยชน์และต้องการสำรวจเทคนิคที่เกี่ยวข้อง ดูบทความของเราเรื่อง วิธีการวิเคราะห์ตัวแปรคั่นกลางใน R Mediation Analysis ช่วยให้คุณเข้าใจ 'อย่างไร' และ 'ทำไม' ของความสัมพันธ์ ในขณะที่ Moderation Analysis เปิดเผย 'เมื่อใด' และ 'สำหรับใคร' - เมื่อรวมกัน ให้ข้อมูลเชิงลึกที่ครอบคลุมเกี่ยวกับความสัมพันธ์ของตัวแปร
นอกจากนี้ หากคุณต้องการเข้าใจพื้นฐานของ Regression ให้ลึกซึ้งยิ่งขึ้น แนะนำให้อ่าน Linear Regression คืออะไร? วิธีการวิเคราะห์ใน SPSS และ ตัวแปรกำกับ คืออะไร? วิธีการวิเคราะห์ใน SPSS
ขอให้โชคดีในการวิเคราะห์!