ค่าสัมประสิทธิ์แอลฟาของครอนบาค (Cronbach's Alpha) ในโปรแกรม SPSS เป็นการทดสอบความเชื่อมั่น (Reliability Test) ที่ใช้วัดความสอดคล้องภายในของข้อคำถามในแบบสอบถามและการสำรวจ การเรียนรู้ วิธีการคำนวณค่าสัมประสิทธิ์แอลฟาของครอนบาคใน SPSS เป็นทักษะสำคัญสำหรับการตรวจสอบความเที่ยงตรงของ Likert Scale และเครื่องมือวัดหลายรายการในงานวิจัย
คู่มือนี้ครอบคลุม สูตรสัมประสิทธิ์แอลฟาของครอนบาค ขั้นตอนการคำนวณแบบละเอียด การ ตีความผล จากโปรแกรม SPSS และค่าความเชื่อมั่นที่ยอมรับได้ คุณจะได้เรียนรู้ว่า ค่าสัมประสิทธิ์แอลฟาของครอนบาคที่ยอมรับได้ คือเท่าไหร่ (ค่ามากกว่า 0.70 สำหรับงานวิจัยส่วนใหญ่ แม้ว่า 0.50-0.60 อาจยอมรับได้สำหรับแบบวัดที่มีข้อคำถามน้อย)
วิธีการคำนวณค่าความเชื่อมั่นของแบบสอบถาม โดยใช้ค่าแอลฟาของครอนบาคเป็นทักษะที่จำเป็นสำหรับนักวิจัยที่ต้องการทำการวิเคราะห์ความเชื่อมั่นใน SPSS
ค่าสัมประสิทธิ์แอลฟาของครอนบาค คืออะไร?
ค่าสัมประสิทธิ์แอลฟาของครอนบาค (Cronbach's Alpha) เป็นหนึ่งในการทดสอบความเชื่อมั่นที่ใช้กันอย่างแพร่หลายที่สุดสำหรับการวัดความสอดคล้องภายใน (Internal Consistency) ของข้อคำถามในแบบสอบถามที่เป็นมาตราส่วนอันดับหรือมาตราส่วนอัตราส่วน
สิ่งสำคัญในงานวิจัยทางองค์กรและสังคมศาสตร์ คือ การตรวจสอบความเที่ยงตรงของเครื่องมือวัดก่อนที่จะดำเนินการวิเคราะห์ขั้นสูง เช่น การวิเคราะห์ตัวแปรคั่นกลาง หรือ การวิเคราะห์ตัวแปรกำกับ
ค่าแอลฟาของครอนบาคใช้ทำอะไร?
ค่าแอลฟาของครอนบาคช่วยให้นักวิจัยทราบว่าข้อคำถามในแบบสอบถามมีความสอดคล้องกันหรือไม่ กล่าวคือ ข้อคำถามทั้งหมดวัดสิ่งเดียวกันหรือแนวคิดเดียวกัน (Construct) อย่างสม่ำเสมอหรือไม่
ทำความเข้าใจสูตรสัมประสิทธิ์แอลฟาของครอนบาค
สูตรสัมประสิทธิ์แอลฟาของครอนบาคคำนวณว่าชุดของข้อคำถามวัดแนวคิดพื้นฐานเดียว (Underlying Construct) ได้ดีเพียงใด นี่คือสูตรทางคณิตศาสตร์:
สัญลักษณ์ในสูตร:
- α = ค่าสัมประสิทธิ์แอลฟาของครอนบาค (มีค่าระหว่าง 0 ถึง 1)
- N = จำนวนข้อคำถามในแบบวัด
- c̅ = ค่าเฉลี่ยของความแปรปรวนร่วม (Covariance) ระหว่างคู่ข้อคำถาม
- v̅ = ค่าเฉลี่ยของความแปรปรวน (Variance) ของข้อคำถามทั้งหมด
สูตรนี้บอกอะไรเรา?
สูตรนี้เปรียบเทียบค่าสหสัมพันธ์เฉลี่ยระหว่างข้อคำถาม (Covariance) กับความแปรปรวนรวมในแบบวัด ความสัมพันธ์ระหว่างข้อคำถามที่สูงกว่าจะนำไปสู่ค่าแอลฟาที่สูงขึ้น ซึ่งบ่งชี้ว่าข้อคำถามวัดแนวคิดเดียวกันอย่างสม่ำเสมอ
ปัจจัยสำคัญที่มีผลต่อค่าแอลฟาของครอนบาค:
- จำนวนข้อคำถาม (N): ข้อคำถามที่มากขึ้นโดยทั่วไปจะเพิ่มค่าแอลฟา แต่การเพิ่มข้อคำถามที่ซ้ำซ้อนอาจทำให้ค่าแอลฟาสูงเกินจริง
- ความสัมพันธ์ระหว่างข้อคำถาม: ข้อคำถามควรมีความสัมพันธ์ในระดับปานกลาง (0.30-0.70) ซึ่งกันและกัน
- ความแปรปรวนของแบบวัด: ความแปรปรวนที่ต่ำภายในข้อคำถามอาจลดค่าแอลฟา
สูตรทางเลือก (ใช้ความสัมพันธ์ระหว่างข้อคำถาม):
โดย r̅ แทนค่าเฉลี่ยของความสัมพันธ์ระหว่างข้อคำถาม สูตรนี้แสดงให้เห็นชัดเจนยิ่งขึ้นว่าจำนวนข้อคำถามและความสัมพันธ์เฉลี่ยของพวกเขากำหนดความเชื่อมั่นอย่างไร
"ข้อคำถาม" (Item) คืออะไร? ในการวิเคราะห์ความเชื่อมั่น "ข้อคำถาม" หมายถึงคำถามเดียวในแบบสอบถามของคุณ นี่คือตัวอย่างของข้อคำถาม Likert Scale:
| ข้อคำถาม | ไม่เห็นด้วยอย่างยิ่ง | ไม่เห็นด้วย | เป็นกลาง | เห็นด้วย | เห็นด้วยอย่างยิ่ง |
|---|---|---|---|---|---|
| ฉันชอบซื้อของชำทางออนไลน์ | ☐ | ☐ | ☐ | ☐ | ☐ |
ตัวอย่างของข้อคำถาม Likert Scale แบบ 5 ระดับ (1 = ไม่เห็นด้วยอย่างยิ่ง ถึง 5 = เห็นด้วยอย่างยิ่ง)
ตัวอย่างนี้ใช้ Likert Scale 5 ระดับ โดย 1 = ไม่เห็นด้วยอย่างยิ่ง; 2 = ไม่เห็นด้วย; 3 = เป็นกลาง; 4 = เห็นด้วย; และ 5 = เห็นด้วยอย่างยิ่ง
แบบสอบถามโดยทั่วไปมีหลายข้อคำถามที่วัดแนวคิดเดียวกัน (ตัวแปรมาตราส่วน) ในการวิจัยทางสถิติ สิ่งสำคัญคือต้องตรวจสอบว่าข้อคำถามภายในมาตราส่วนมีความสัมพันธ์กัน ซึ่งหมายความว่าพวกเขาวัดแนวคิดพื้นฐานเดียวกันและค่าของพวกเขาแปรผันไปด้วยกัน
ค่าสัมประสิทธิ์แอลฟาของครอนบาคมีค่าตั้งแต่ 0 ถึง 1 โดย ค่าแอลฟามากกว่า 0.70 โดยทั่วไปถือว่ายอมรับได้ ค่าที่ใกล้เคียงกับ 1 บ่งชี้ถึงความเชื่อมั่นที่แข็งแกร่งกว่า นี่คือวิธีการตีความค่าแอลฟาที่แตกต่างกัน:
ตารางตีความค่าสัมประสิทธิ์แอลฟาของครอนบาค
| ค่าแอลฟาของครอนบาค | ความสอดคล้องภายใน | คำแนะนำ |
|---|---|---|
| α ≥ 0.90 | ดีเยี่ยม (Excellent) | พิจารณาว่ามีความซ้ำซ้อนหรือไม่ ความเชื่อมั่นที่สูงเกินไปอาจบ่งชี้ว่าข้อคำถามซ้ำกัน |
| α = 0.80 - 0.89 | ดี (Good) | ยอมรับได้สำหรับงานวิจัยทางวิชาการและการประยุกต์ใช้ส่วนใหญ่ |
| α = 0.70 - 0.79 | ยอมรับได้ (Acceptable) | เกณฑ์มาตรฐาน เหมาะสำหรับแบบวัดใหม่หรือการศึกษาเชิงสำรวจ |
| α = 0.60 - 0.69 | น่ากังวล (Questionable) | พิจารณาปรับปรุงข้อคำถาม ยอมรับได้เฉพาะในการวิจัยระยะเริ่มต้นเท่านั้น |
| α = 0.50 - 0.59 | แย่ (Poor) | ต้องปรับปรุง ไม่แนะนำสำหรับการตีพิมพ์ |
| α < 0.50 | ไม่ยอมรับ (Unacceptable) | ปฏิเสธแบบวัด ต้องออกแบบใหม่ทั้งหมด |
คำแนะนำการตีความค่าสัมประสิทธิ์แอลฟาของครอนบาคสำหรับการวิเคราะห์ความเชื่อมั่น
ข้อยกเว้นที่สำคัญ: สำหรับแบบวัดที่มีน้อยกว่า 10 ข้อคำถาม ค่าแอลฟา > 0.50 อาจถือว่ายอมรับได้ (Pallant, 2010) แม้ว่าค่ามากกว่า 0.70 จะยังคงเป็นที่ต้องการ
เมื่อคำนวณค่าสัมประสิทธิ์แอลฟาของครอนบาคใน SPSS ให้คำนวณค่าความเชื่อมั่นแยกสำหรับแต่ละมาตราส่วน อย่ารวมคำถามทุกข้อในการวิเคราะห์เดียว
ตัวอย่างการทดสอบความเชื่อมั่นใน SPSS
ตัวอย่างนี้ใช้แบบสอบถามที่วัดความตั้งใจซื้อออนไลน์ด้วยตัวแปรมาตราส่วนสองตัว: พฤติกรรมผู้บริโภค และ ความตั้งใจซื้อ แต่ละตัวแปรมี 4 ข้อคำถามที่วัดด้วย Likert Scale 5 ระดับ
เป้าหมาย: คำนวณค่าสัมประสิทธิ์แอลฟาของครอนบาคสำหรับแต่ละมาตราส่วน
ชุดข้อมูลสำหรับฝึกปฏิบัติ: ดาวน์โหลดชุดข้อมูล SPSS จากส่วนดาวน์โหลดด้านบน (ข้อมูลจำลองสำหรับการศึกษาเท่านั้น) แตกไฟล์ zip และดับเบิลคลิกไฟล์ .sav เพื่อเปิดใน SPSS
วิธีการคำนวณค่าสัมประสิทธิ์แอลฟาของครอนบาคใน SPSS
ไฟล์ตัวอย่าง SPSS ที่ดาวน์โหลดด้านบนมีชุดข้อมูลสำหรับ 30 ตัวอย่างและมีลักษณะดังนี้:
 ภาพรวมของชุดข้อมูลตัวอย่าง SPSS ที่มีตัวแปรมาตราส่วนสองตัว
ภาพรวมของชุดข้อมูลตัวอย่าง SPSS ที่มีตัวแปรมาตราส่วนสองตัว
ชุดข้อมูลประกอบด้วยสองมาตราส่วน: พฤติกรรมผู้บริโภค (CB) ที่มี 4 ข้อคำถาม (CB1-CB4) และ ความตั้งใจซื้อ (PI) ที่มี 4 ข้อคำถาม (PI1-PI4)
ข้อคำถามทั้งหมดใช้ Likert Scale 5 ระดับ โดย 1 = ไม่เห็นด้วยอย่างยิ่ง, 2 = ไม่เห็นด้วย, 3 = เป็นกลาง, 4 = เห็นด้วย, และ 5 = เห็นด้วยอย่างยิ่ง
ชุดข้อมูลของคุณอาจใหญ่กว่าและมีมากกว่าสองตัวแปรมาตราส่วน อย่างไรก็ตาม กระบวนการวิเคราะห์ความเชื่อมั่นใน SPSS เหมือนกัน
ขั้นตอนที่ 1: บนเมนูด้านบนของ SPSS ไปที่ Analyze → Scale → Reliability Analysis
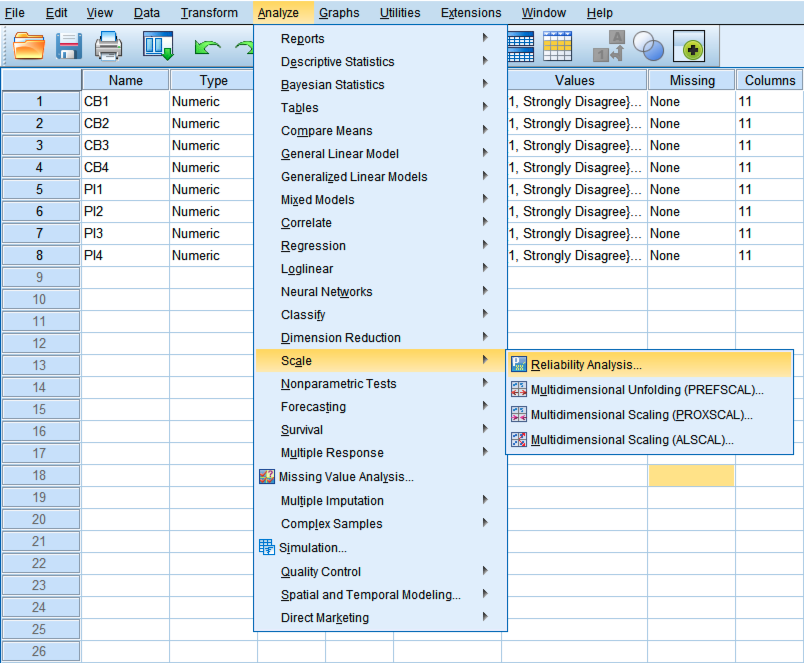 การเข้าถึง Reliability Analysis จากเมนู Analyze ใน SPSS
การเข้าถึง Reliability Analysis จากเมนู Analyze ใน SPSS
ขั้นตอนที่ 2: ในหน้าต่าง Reliability Analysis ของ SPSS เลือกข้อคำถามทั้งหมดที่วัดตัวแปรหนึ่งตัว (เช่น พฤติกรรมผู้บริโภค) จากบล็อกซ้ายและใช้ปุ่มลูกศรเพื่อย้ายไปทางขวา
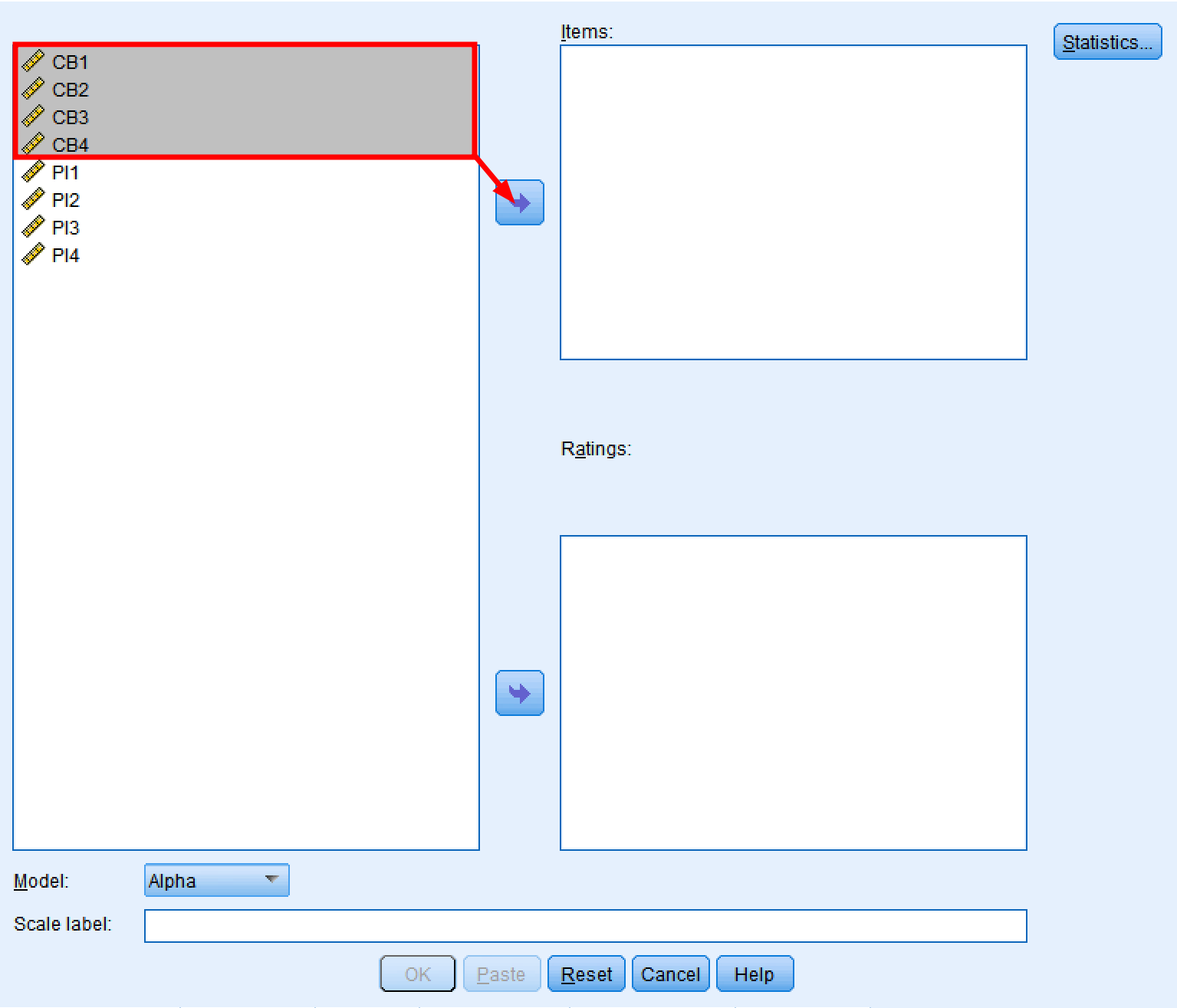 การเลือกข้อคำถามมาตราส่วน (CB1-CB4) สำหรับการวิเคราะห์ความเชื่อมั่นด้วยค่าแอลฟาของครอนบาค
การเลือกข้อคำถามมาตราส่วน (CB1-CB4) สำหรับการวิเคราะห์ความเชื่อมั่นด้วยค่าแอลฟาของครอนบาค
ขั้นตอนที่ 3: ตรวจสอบให้แน่ใจว่า Model ที่เลือกคือ Alpha
 การตั้งค่าโมเดลความเชื่อมั่นเป็น Alpha สำหรับการคำนวณค่าแอลฟาของครอนบาค
การตั้งค่าโมเดลความเชื่อมั่นเป็น Alpha สำหรับการคำนวณค่าแอลฟาของครอนบาค
ขั้นตอนที่ 4: พิมพ์ชื่อในบล็อก Scale label ขั้นตอนนี้ไม่บังคับ แต่สามารถช่วยในการตีความผลการวิเคราะห์ความเชื่อมั่นใน SPSS
 การเพิ่มป้ายกำกับมาตราส่วนที่อธิบายเพื่อการตีความผลที่ง่ายขึ้น
การเพิ่มป้ายกำกับมาตราส่วนที่อธิบายเพื่อการตีความผลที่ง่ายขึ้น
ขั้นตอนที่ 5: คลิกปุ่ม Statistics เราต้องเลือกตัวเลือกบางอย่างสำหรับการวิเคราะห์ความเชื่อมั่นก่อน
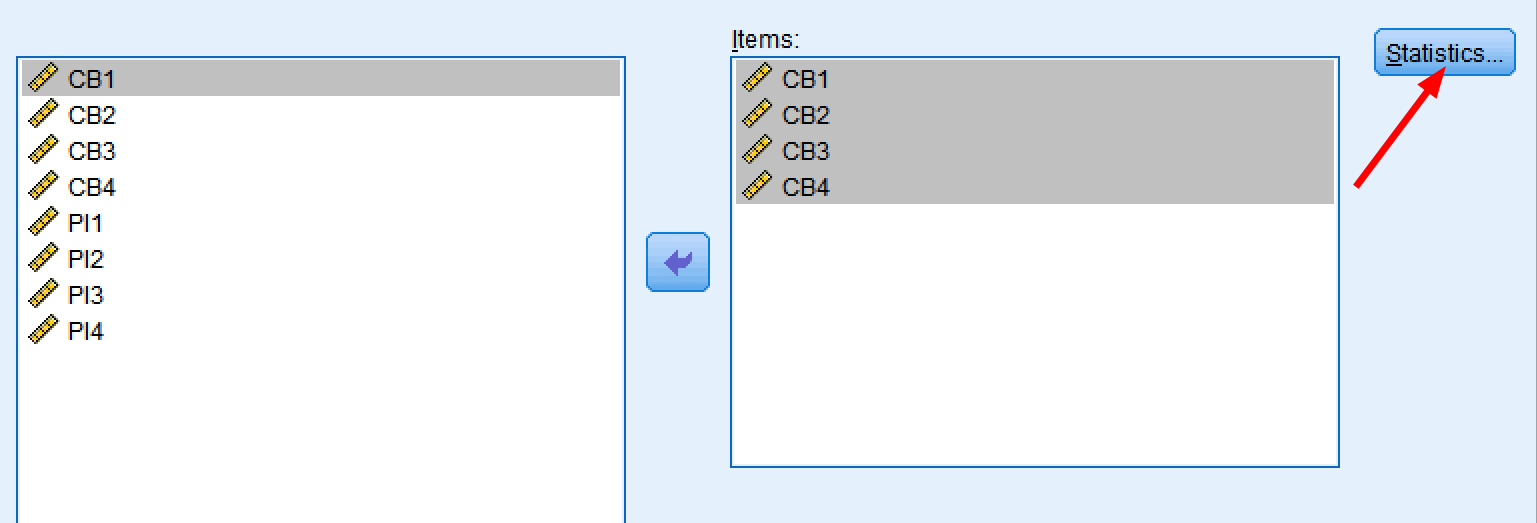 การเข้าถึงตัวเลือก Statistics สำหรับผลลัพธ์ความเชื่อมั่นโดยละเอียด
การเข้าถึงตัวเลือก Statistics สำหรับผลลัพธ์ความเชื่อมั่นโดยละเอียด
ขั้นตอนที่ 6: จากแท็บ Statistics เลือก Items, Scale, และ Scale if item deleted ภายใต้ส่วน Descriptive for ในส่วน Summarize เลือก Means และ Correlations สุดท้าย ภายใต้ Inter-item เลือก Correlations คลิก Continue จากนั้น OK เพื่อดำเนินการวิเคราะห์
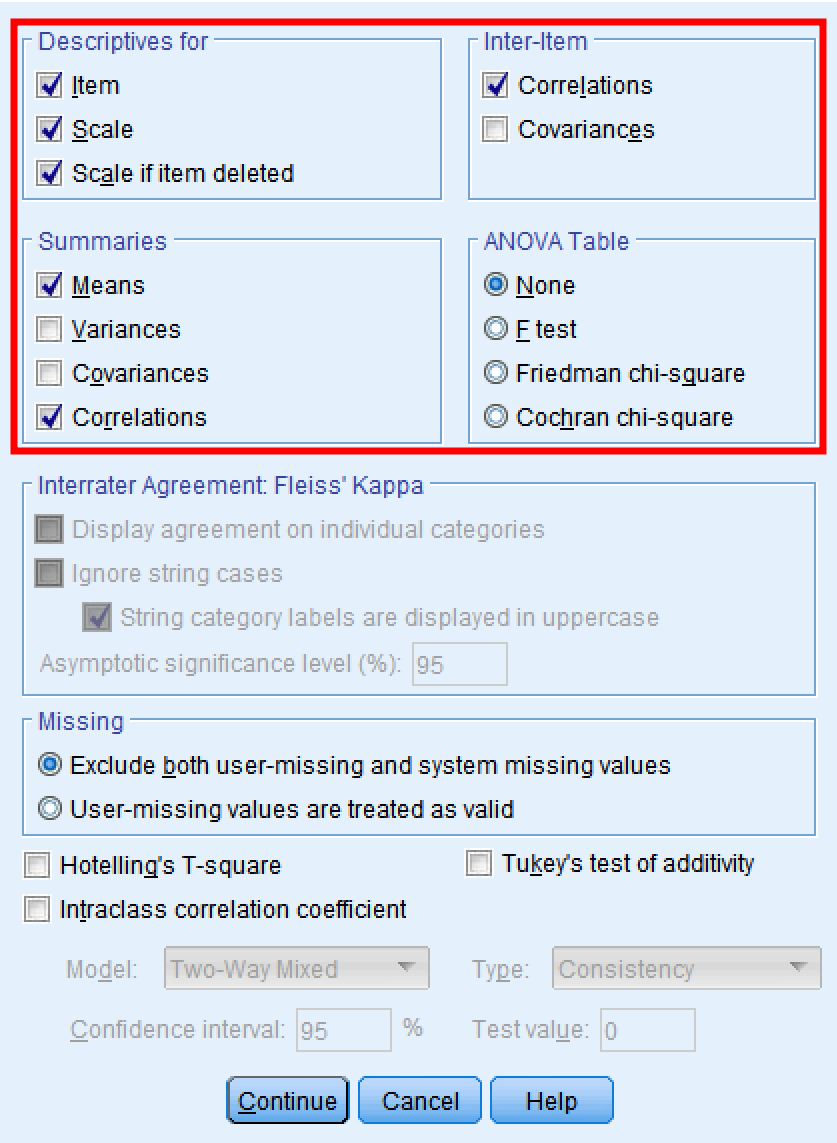 การกำหนดค่าตัวเลือกสถิติสำหรับผลลัพธ์ค่าแอลฟาของครอนบาคที่ครอบคลุมใน SPSS
การกำหนดค่าตัวเลือกสถิติสำหรับผลลัพธ์ค่าแอลฟาของครอนบาคที่ครอบคลุมใน SPSS
การตีความผลค่าสัมประสิทธิ์แอลฟาของครอนบาค
ดีมาก ตอนนี้คุณควรเห็นผลลัพธ์ความเชื่อมั่นแอลฟาในหน้าต่าง SPSS ใหม่ ต่อไป มาดูการตีความผลค่าแอลฟาของครอนบาคกันเลย
สรุปการประมวลผลข้อมูล (Case Processing Summary)
Case Processing Summary คือตารางแรกในผลลัพธ์ความเชื่อมั่นที่แสดงสรุปของกรณีที่ประมวลผลในการวิเคราะห์นี้ เราสามารถสังเกตได้ว่ามี 30 กรณีที่ประมวลผล (N = 30 ตัวอย่าง) เรายังเห็นว่าไม่มีกรณีใดถูกยกเว้น (100% ของขนาดตัวอย่างรวมอยู่ในการวิเคราะห์)
หากการประมาณสรุปของคุณต่ำกว่า 100% ตัวอย่าง (N Valid ≠ N Total) คุณควรตรวจสอบชุดข้อมูลของคุณเพื่อหาข้อผิดพลาด ช่องว่าง หรือ (ส่วนใหญ่) ค่าที่ขาดหายไป
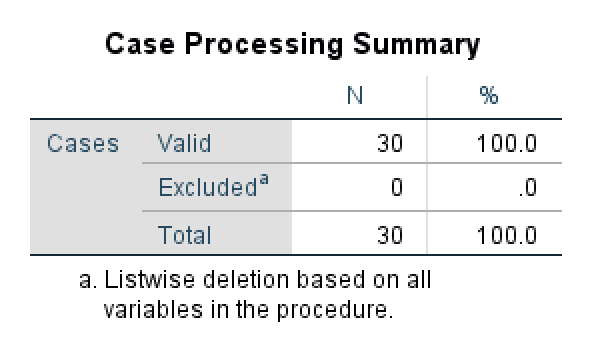 Case Processing Summary แสดงกรณีทั้งหมด 30 กรณีรวมอยู่ในการวิเคราะห์ความเชื่อมั่น
Case Processing Summary แสดงกรณีทั้งหมด 30 กรณีรวมอยู่ในการวิเคราะห์ความเชื่อมั่น
สถิติความเชื่อมั่น (Reliability Statistics)
ตาราง Reliability Statistics แสดงให้เราเห็นค่าสัมประสิทธิ์แอลฟาความเชื่อมั่นสำหรับข้อคำถามทั้งหมดที่รวมอยู่ในการวิเคราะห์ ในตัวอย่างของเรา ค่าแอลฟาคือ 0.904 (> 0.7) ซึ่งตีความว่าดีเยี่ยม
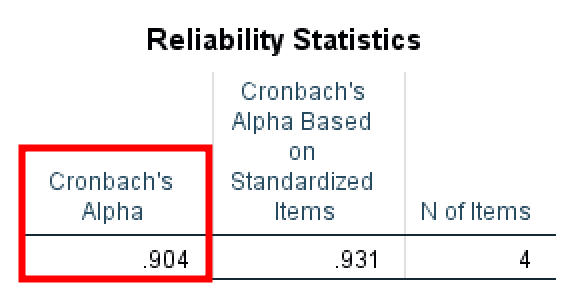 ตาราง Reliability Statistics แสดงค่าแอลฟาของครอนบาคที่ดีเยี่ยมที่ 0.904
ตาราง Reliability Statistics แสดงค่าแอลฟาของครอนบาคที่ดีเยี่ยมที่ 0.904
สิ่งสำคัญคือต้องจำไว้ว่าหากคุณมีน้อยกว่า 10 ข้อคำถามในมาตราส่วน จะค่อนข้างยากที่จะได้ค่าแอลฟาที่สูง ในกรณีเช่นนั้น ค่าแอลฟา > 0.5 ถือว่ายอมรับได้ (Pallant, 2010) ค่าที่ต่ำกว่า < 0.5 ควรเป็นสาเหตุที่น่ากังวลในกรณีดังกล่าว
สถิติข้อคำถาม (Item Statistics)
ตาราง Item Statistics ให้ข้อมูลเกี่ยวกับค่าเฉลี่ย ส่วนเบี่ยงเบนมาตรฐาน และจำนวนตัวอย่าง (N) สำหรับแต่ละข้อคำถามในมาตราส่วน ค่าเฉลี่ยแทนค่าเฉลี่ยของค่าในชุดข้อมูลและมีประโยชน์เมื่อวิเคราะห์สถิติเชิงพรรณนาหรือความถี่ในการศึกษาของเรา
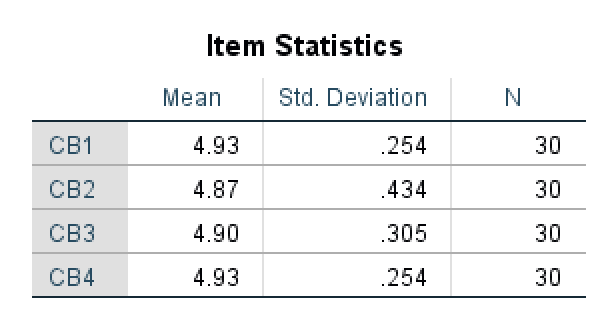 Item Statistics แสดงสถิติเชิงพรรณนาสำหรับแต่ละข้อคำถามในมาตราส่วน
Item Statistics แสดงสถิติเชิงพรรณนาสำหรับแต่ละข้อคำถามในมาตราส่วน
เมทริกซ์สหสัมพันธ์ระหว่างข้อคำถาม (Inter-Item Correlation Matrix)
เมทริกซ์สหสัมพันธ์ระหว่างข้อคำถามแสดงให้เราเห็นว่าข้อคำถามในมาตราส่วนมีความสัมพันธ์กันอย่างไร ค่าสูงสุดที่นี่คือ 1.000 เมื่อข้อคำถามมีความสัมพันธ์กับตัวเองในเมทริกซ์ ค่าสหสัมพันธ์ที่สูงแสดงความสัมพันธ์ที่แข็งแกร่งระหว่างสองข้อคำถามในมาตราส่วน
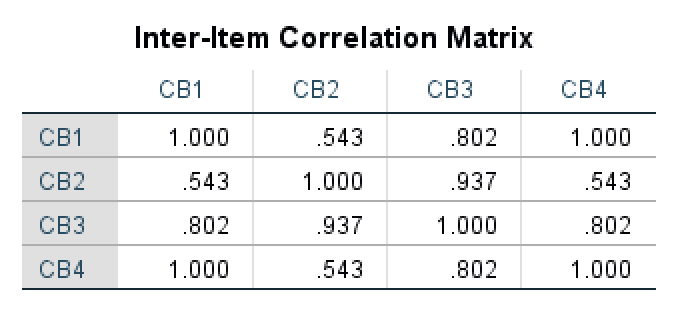 Inter-Item Correlation Matrix แสดงความสัมพันธ์ระหว่างข้อคำถามในมาตราส่วน
Inter-Item Correlation Matrix แสดงความสัมพันธ์ระหว่างข้อคำถามในมาตราส่วน
ในตัวอย่างของเรา เราสามารถเห็นได้ว่าข้อคำถาม CB2 และ CB3 มีความสัมพันธ์สูง (0.937) บ่งชี้ความสัมพันธ์ที่แข็งแกร่ง ในทางตรงกันข้าม ความสัมพันธ์ระหว่าง CB4 และ CB2 (0.543) ไม่แข็งแกร่งนัก บ่งชี้ความสัมพันธ์ที่อ่อนแอกว่าระหว่างข้อคำถามเหล่านี้
สถิติสรุปข้อคำถาม (Summary Item Statistics)
ตาราง Summary Item Statistics แสดงให้เราเห็นค่าเฉลี่ยสำหรับข้อคำถามทั้งหมดในมาตราส่วนและข้อคำถามเหล่านี้มีความสัมพันธ์กันอย่างไร นอกจากนี้ยังแสดงช่วงของค่าเฉลี่ยที่คำนวณเป็นความแตกต่างระหว่างค่าสูงสุดและค่าต่ำสุด
 Summary Item Statistics แสดงค่าเฉลี่ยสหสัมพันธ์ระหว่างข้อคำถามที่ 0.771
Summary Item Statistics แสดงค่าเฉลี่ยสหสัมพันธ์ระหว่างข้อคำถามที่ 0.771
หากคุณมีค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างข้อคำถามที่ต่ำสำหรับค่าเฉลี่ย (< 0.5) เนื่องจากจำนวนข้อคำถามในมาตราส่วนที่ต่ำ สิ่งสำคัญคือต้องรายงานในการวิเคราะห์ของคุณ (Pallant, 2010) ในกรณีของเรา ค่าเฉลี่ยสหสัมพันธ์ระหว่างข้อคำถามคือ 0.771 (> 0.7) ดังนั้นจึงยอมรับได้
สถิติข้อคำถาม-รวม (Item-Total Statistics)
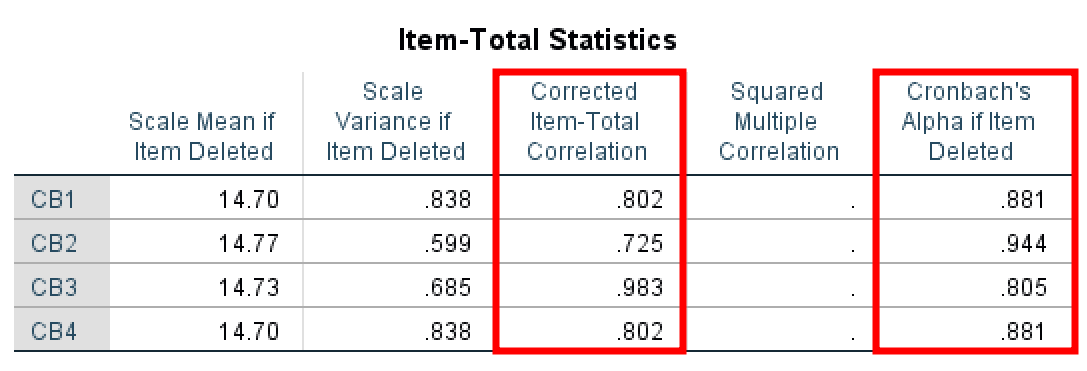
ตาราง Item Total Statistics แสดงค่าเฉลี่ยของมาตราส่วนและความแปรปรวนหากลบข้อคำถามเฉพาะออก สหสัมพันธ์รวมสำหรับข้อคำถามที่แก้ไข สหสัมพันธ์พหุคูณกำลังสอง และค่าของสัมประสิทธิ์แอลฟาของครอนบาคหากลบข้อคำถามออก
 Item-Total Statistics สำหรับการระบุข้อคำถามที่มีปัญหาในมาตราส่วน
Item-Total Statistics สำหรับการระบุข้อคำถามที่มีปัญหาในมาตราส่วน
มาดูคอลัมน์ Corrected item – Total Correlation ก่อน ค่าที่นี่แทนความสัมพันธ์ของแต่ละข้อคำถามกับข้อคำถามที่เหลือรวมกัน เช่น ข้อคำถาม CB1 (0.802) มีความสัมพันธ์กับข้อคำถาม CB2, CB3, CB4; ข้อคำถาม CB2 มีความสัมพันธ์กับข้อคำถาม CB1, CB3, และ CB4; และอื่นๆ คุณควรมุ่งเป้าที่ค่า > 0.40 ที่นี่
ต่อไป มาวิเคราะห์คอลัมน์ Cronbach's Alpha if Item Deleted นี่สำคัญเมื่อต้องจัดการกับคะแนนแอลฟาที่แย่และเราต้องการระบุว่าข้อคำถามใดเป็นสาเหตุ คอลัมน์นี้บอกเราว่าหากลบข้อคำถามออก ค่าแอลฟาที่เกิดขึ้นจะเป็นเท่าไหร่
สถิติมาตราส่วน (Scale Statistics)
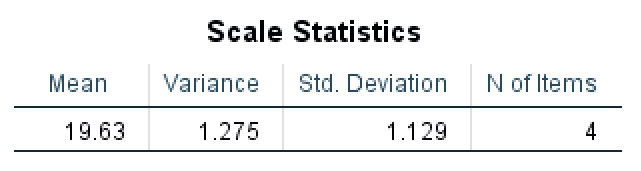
สุดท้าย ตาราง Scale Statistics แสดงค่าเฉลี่ย ความแปรปรวน และส่วนเบี่ยงเบนมาตรฐานที่คำนวณสำหรับทั้งมาตราส่วน
 Scale Statistics แสดงสถิติเชิงพรรณนาโดยรวมสำหรับมาตราส่วนที่สมบูรณ์
Scale Statistics แสดงสถิติเชิงพรรณนาโดยรวมสำหรับมาตราส่วนที่สมบูรณ์
ตอนนี้ลองทำตามสิ่งที่คุณเรียนรู้โดยการทดสอบความเชื่อมั่นใน SPSS สำหรับตัวแปรมาตราส่วนที่สองในตัวอย่างของเรา: ความตั้งใจซื้อ
มันผ่านการทดสอบความเชื่อมั่นแอลฟาหรือไม่?
คำถามที่พบบ่อย
สรุป
การวิเคราะห์ความเชื่อมั่นเป็นสิ่งจำเป็นในการวิจัยทางสถิติและทำหน้าที่เป็นสมมติฐานสำหรับการวิเคราะห์ขั้นสูง เช่น การวิเคราะห์ถดถอยเชิงเส้นพหุคูณ ค่าแอลฟามากกว่า 0.70 บ่งชี้ความเชื่อมั่นที่ยอมรับได้ หากค่าแอลฟาของคุณต่ำกว่าเกณฑ์นี้ ให้ตรวจสอบตาราง Item-Total Statistics เพื่อระบุข้อคำถามที่มีปัญหา
ตอนนี้คุณทราบวิธีการคำนวณค่าสัมประสิทธิ์แอลฟาของครอนบาคใน SPSS ตีความผลลัพธ์ และประเมินความเชื่อมั่นของมาตราส่วนสำหรับงานวิจัยของคุณแล้ว
ไม่มีโปรแกรม SPSS? คุณยังสามารถ คำนวณค่าสัมประสิทธิ์แอลฟาของครอนบาคใน Excel โดยใช้วิธีการที่ใช้สูตร
เอกสารอ้างอิง
Bonett, D. G., & Wright, T. A. (2015). Cronbach's Alpha Reliability Interval Estimation, Hypothesis Testing, and Sample Size Planning.
Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika, 16, 297-334 (28,307 citations in Google Scholar as of 4/1/2016).
Pallant, Julie. SPSS Survival Manual: A Step by Step Guide to Data Analysis Using SPSS. Maidenhead: Open University Press/McGraw-Hill, 2010.