Pearson Correlation in Excel: Step-by-Step Guide (CORREL Function)

Learn how to calculate the Pearson correlation coefficient in Excel using the CORREL function and Data Analysis Toolpak. This step-by-step guide shows you how to measure the correlation between two variables, interpret results, and check assumptions.

The Pearson correlation coefficient measures the strength and direction of the linear relationship between two continuous variables. Excel's built-in CORREL function makes it easy to calculate correlation coefficients quickly, whether you're analyzing advertising spend vs revenue, test scores vs study hours, or any two related variables.

Download the practice dataset from the sidebar (password: uedufy) and follow along with the examples.

What is Pearson correlation coefficient?

Let's say you own a clothing store and want to see if there is a relationship between how much you spend on advertising and how much money you make. This is where the Pearson correlation coefficient comes in handy!

On the other hand, if the coefficient is close to -1, that means that as you spend more on advertising, your income is likely to decrease. And if the coefficient is close to 0, there's no real relationship between advertising and revenue.

You looked at your data, and the Pearson correlation coefficient was 0.8. This means there's a strong positive relationship between Advertising and Revenue: the more you spend on advertising, the more money you make! But don't get too excited just yet. Other factors can affect income too. Knowing the Pearson correlation coefficient is just one piece of the puzzle, but an important metric to consider.

The Pearson correlation coefficient measures the strength of the relationship between two things, in this case, advertising and revenue. If the coefficient is close to 1, that means that as you spend more on advertising, you'll likely see an increase in revenue.

$r=\frac{\sum\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum\left(x_i-\bar{x}\right)^2 \sum\left(y_i-\bar{y}\right)^2}}$

Where:

r is the correlation coefficient
xi represents values of the x-variable in a sample
x̄ is the mean of the values of the x-variable
yi represents values of the y-variable in a sample
ȳ is the mean of the values of the y-variable

Pearson Correlation Assumptions

Before calculating Pearson correlation coefficient in Excel, verify your data meets these assumptions:

1. Continuous Variables

Both variables should be measured on a continuous scale (interval or ratio level). Pearson correlation is NOT appropriate for categorical or ordinal data.

Examples of continuous variables: height, weight, temperature, test scores, revenue, time

2. Linearity

The relationship between the two variables should be linear. This means that as one variable increases, the other variable increases (or decreases) at a constant rate.

How to check in Excel: Create a scatter plot of your data. If the points roughly form a straight line pattern (not a curve), the linearity assumption is met.

3. Independence of Observations

Each observation should be independent, meaning that the value of one observation should not influence or be related to the value of another observation.

Example: Measuring the same person multiple times violates independence. Each data point should come from a different subject or measurement occasion.

4. Bivariate Normality

For accurate significance testing, both variables should follow a bivariate normal distribution. However, Pearson correlation is fairly robust to violations of normality for larger sample sizes (n > 30).

How to check in Excel: Create histograms for each variable to visually assess normality. For samples smaller than 30, consider using normality tests.

What if assumptions are violated?

If your data violates these assumptions (especially linearity or normality), consider using Spearman's rank correlation coefficient instead, which is a non-parametric alternative that doesn't require these strict assumptions.

Method 1: Calculate correlation coefficient in Excel using CORREL function

Let's go back to our clothing store example and learn how to calculate Pearson correlation coefficient in Excel to find out if there is a relationship between how much we spend on advertising and how much money we make.

1. Prepare your data: Organize your data into two columns, with one column representing each of the two variables you want to analyze. In my dataset, the two variables we want to check if they are correlated are Advertising and Revenue.

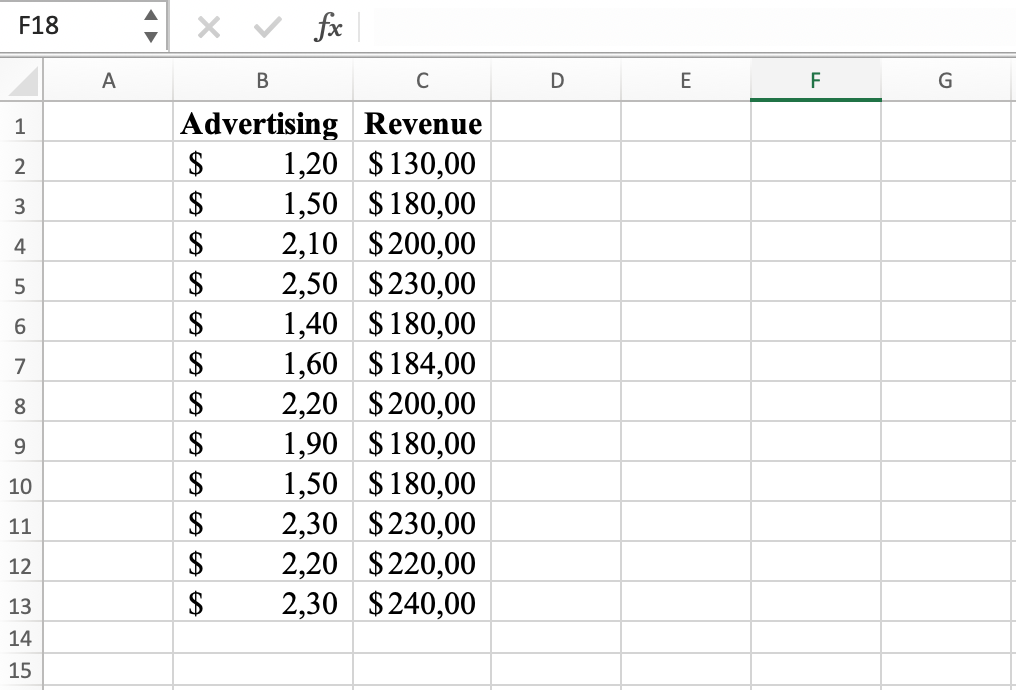Pearson correlation coefficient in Excel dataset showing two columns for Advertising and Revenue variables Example of two variables for correlation coefficient calculation in Excel

2. Select a cell: Choose a cell in your worksheet where you would like to display the result of the Pearson correlation coefficient.

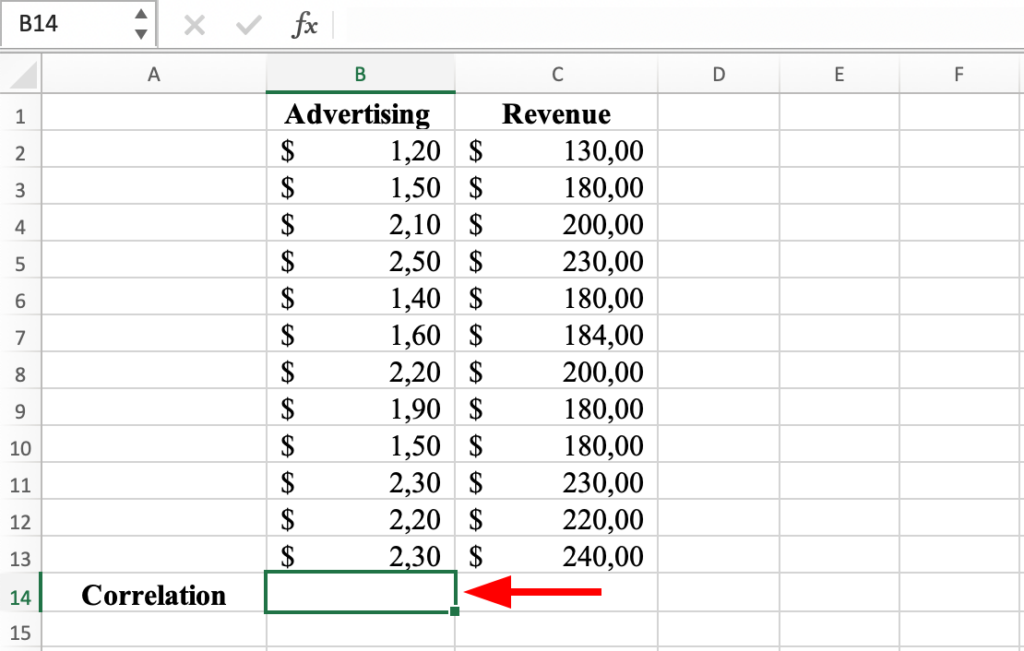Excel worksheet with selected cell for displaying Pearson correlation coefficient result Select a cell in the worksheet for the correlation result

3. Enter the correlation function: Type "=CORREL(" followed by the range of the first column of data, a comma, and the range of the second column of data, and close the parentheses. For example, if your data is in columns B and C (like in the capture below), the correlation function would look like this: =CORREL(B2:B13, C2:C13).

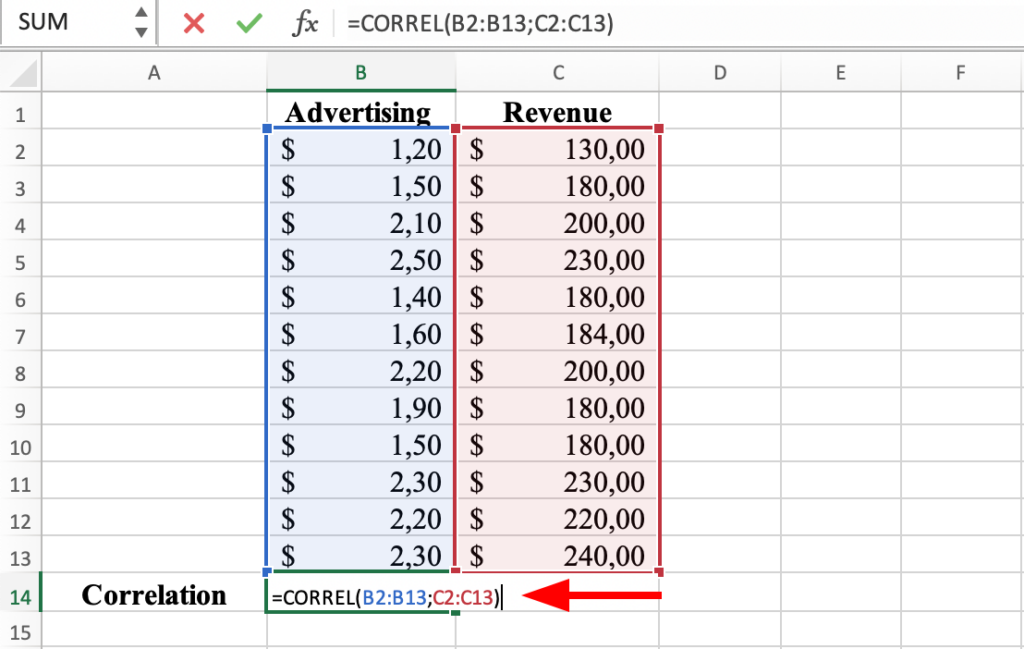Excel showing CORREL function syntax for calculating Pearson correlation coefficient CORREL function in Excel

4. Calculate the result: Press the ENTER key to calculate the Pearson correlation coefficient. The result will be displayed in the selected cell. The correlation coefficient between Advertising and Revenue in our dataset is 0.9.

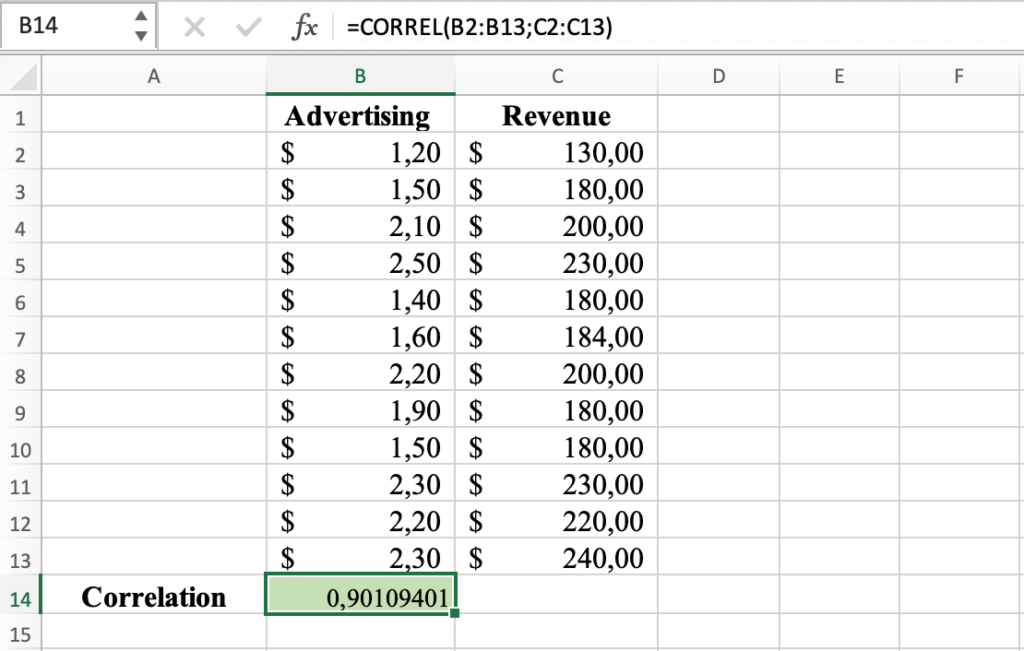Excel displaying Pearson correlation coefficient result of 0.9 Pearson correlation coefficient result for the selected variables

Method 2: Calculate correlation coefficient using Analysis Tool in Excel

Here is another way to calculate the correlation between two variables in Excel using the Data Analysis Toolpak.

1. Prepare your data: Make sure your data is organized in two columns, each column representing a variable (same as we did before).

2. Install Data Analysis tool in Excel: if you don't see the Data Analysis icon in your Data tab in Excel, you should install the Data Analysis Toolpak first.

Excel ribbon showing Data Analysis button location in the Data tab Data Analysis location in Excel

3. Launch the Data Analysis tool: From the Data tab, click on Data Analysis, and select Correlation.

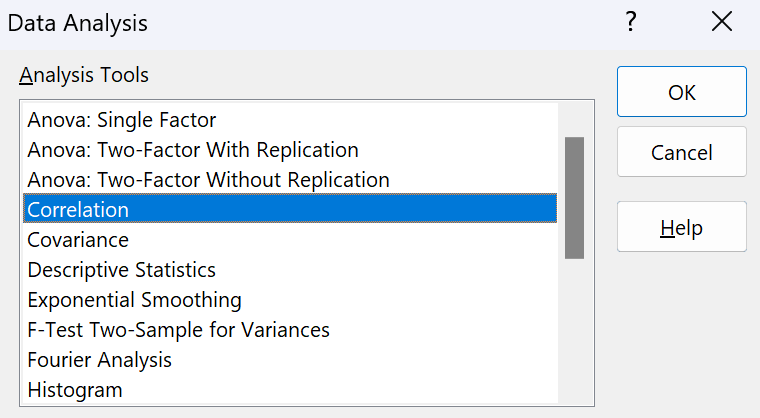Excel Data Analysis dialog box with Correlation option selected Data Analysis - Correlation

4. Select the data: In the Data Analysis dialog box, select the input range, which is the range of the two columns of data. If you included the column labels in your selection (Advertising and Revenue), check the Labels in First Row checkbox.

NOTE: In the "Output Options" section, you can also choose where you want the result to be displayed, either in a new worksheet or in a range of cells. Let's leave the default setting for now.

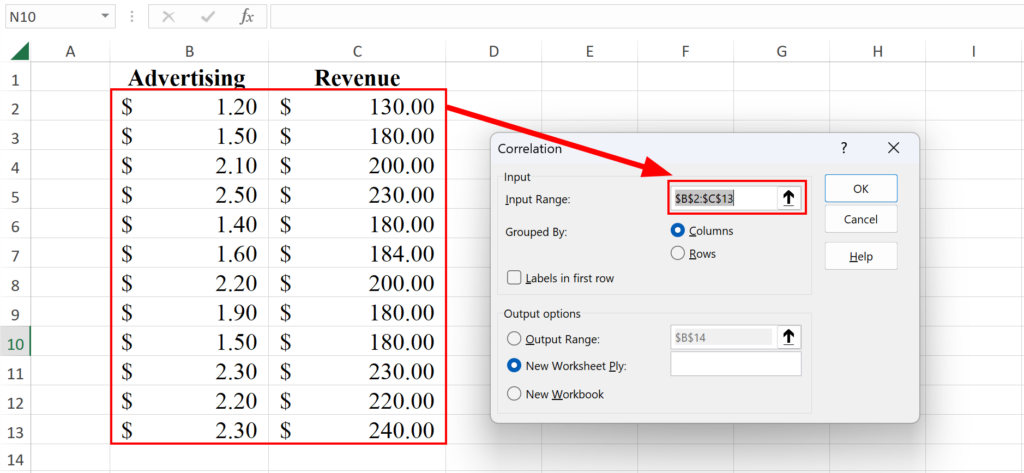Excel Correlation dialog box showing input range selection for Advertising and Revenue data Select the range of values for correlation

5. Run the analysis: Click on OK to compute. The result of the Pearson correlation coefficient will be displayed in the output location you selected. As expected, for the same data set, the coefficient is the same: 0.9.

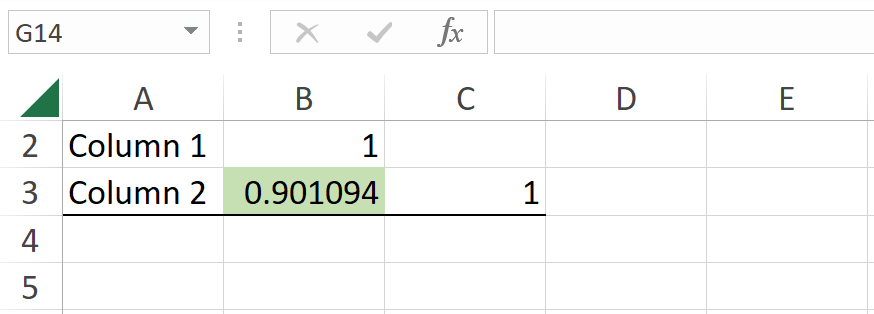Excel output showing Pearson correlation coefficient result of 0.9 using Data Analysis Toolpak Pearson correlation coefficient result in Excel

How to Interpret Pearson Correlation Results

The Pearson correlation coefficient (r) will always be a value between -1 and 1. Here's how to interpret the results in Excel:

Understanding Correlation Values

Coefficient Value:

r = 1: Perfect positive correlation (as one variable increases, the other increases proportionally)
r = -1: Perfect negative correlation (as one variable increases, the other decreases proportionally)
r = 0: No linear correlation (no linear relationship between variables)

Direction:

Positive correlation (0 to 1): Both variables move in the same direction
Negative correlation (0 to -1): Variables move in opposite directions

Correlation Strength Interpretation

Use these guidelines to interpret the strength of your Pearson correlation coefficient:

Correlation Value	Strength	Interpretation
0.9 to 1.0 (or -0.9 to -1.0)	Very strong	Variables are highly correlated
0.7 to 0.9 (or -0.7 to -0.9)	Strong	Strong relationship exists
0.4 to 0.7 (or -0.4 to -0.7)	Moderate	Moderate relationship
0.1 to 0.4 (or -0.1 to -0.4)	Weak	Weak relationship
0 to 0.1 (or 0 to -0.1)	None	No meaningful correlation

Example Interpretation

In our example, the correlation coefficient of r = 0.9 indicates a very strong positive correlation between Advertising and Revenue variables.

What this means:

As advertising spending increases by 1 unit, revenue tends to increase at a very consistent rate
81% of the variance in revenue can be explained by advertising spending (calculated as r² = 0.9² = 0.81)
This is a very strong relationship, but it does not prove causality

Important: Correlation vs Causation

Critical reminder: A high Pearson correlation coefficient does NOT mean one variable causes the other. It only shows they tend to change together.

Why this matters:

Correlation shows association, not causation
A third variable might be influencing both variables
The relationship might be coincidental
Reverse causation might exist (B causes A, not A causes B)

To establish causation, you need experimental research designs or additional statistical methods such as regression analysis.

Pearson vs Spearman Correlation: Which to Use?

When analyzing correlation in Excel, you might wonder whether to use Pearson or Spearman correlation. Here's how to choose the right method:

Pearson Correlation Coefficient

Use Pearson when:

Both variables are continuous (interval or ratio scale)
The relationship between variables is linear
Data is approximately normally distributed
No significant outliers are present

Advantages:

More powerful statistical test (better at detecting true correlations)
Widely recognized and commonly reported in research
Easy to calculate in Excel using CORREL function

Disadvantages:

Sensitive to outliers
Requires assumptions (linearity, normality)
Only detects linear relationships

Spearman Correlation Coefficient

Use Spearman when:

Variables are ordinal (ranked data)
The relationship is monotonic but not necessarily linear
Data contains outliers
Data is not normally distributed

Advantages:

Non-parametric (no distribution assumptions required)
Robust to outliers
Works with ranked/ordinal data
Detects monotonic relationships (not just linear)

Disadvantages:

Less powerful than Pearson when assumptions are met
More complex to calculate in Excel (requires ranking data first)
May miss some relationship nuances

Quick Decision Guide

Choose Pearson correlation if:

Your data is continuous and normally distributed
The scatter plot shows a roughly linear pattern
You have no extreme outliers

Choose Spearman correlation if:

Your data is ordinal/ranked
The scatter plot shows a curved or non-linear pattern
You have significant outliers
Your data violates normality assumptions

Example: If you're correlating test scores (continuous, normally distributed) with study hours (continuous), use Pearson. If you're correlating customer satisfaction rankings (ordinal: 1-5 stars) with product quality ratings, use Spearman.

For most Excel users working with continuous, normally distributed data, Pearson correlation is the appropriate choice.

Frequently Asked Questions

What is the Pearson correlation coefficient?

The Pearson correlation coefficient (also called Pearson's r) is a statistical measure that calculates the strength and direction of the linear relationship between two continuous variables. It ranges from -1 to +1, where -1 indicates a perfect negative correlation, +1 indicates a perfect positive correlation, and 0 indicates no linear correlation.

How do I interpret Pearson correlation results in Excel?

Interpret Pearson correlation values as follows: 0.7 to 1.0 (or -0.7 to -1.0) indicates a strong correlation, 0.4 to 0.7 (or -0.4 to -0.7) indicates a moderate correlation, 0.1 to 0.4 (or -0.1 to -0.4) indicates a weak correlation, and 0 to 0.1 (or 0 to -0.1) indicates no correlation. Positive values mean variables increase together, while negative values mean one increases as the other decreases.

What is the difference between Pearson and Spearman correlation?

Pearson correlation measures linear relationships between continuous variables and assumes bivariate normality. Spearman correlation is a non-parametric test that measures monotonic relationships (not necessarily linear) and works with ranked or ordinal data. Use Pearson when your data is normally distributed and the relationship is linear; use Spearman when data is not normally distributed or contains outliers.

Can Pearson correlation prove causation?

No, Pearson correlation does NOT prove causation. It only measures the strength and direction of association between two variables. A high correlation means variables tend to change together, but it doesn't tell you which variable causes changes in the other, or if a third variable is influencing both. To establish causation, you need experimental research designs or additional statistical methods like regression analysis.

What sample size do I need for Pearson correlation in Excel?

While Pearson correlation can technically be calculated with small samples, you need at least n=30 for reliable results and significance testing. Smaller samples (n<30) are more sensitive to outliers and violations of normality assumptions. For detecting small correlations (r=0.1-0.3), you may need 100+ observations for adequate statistical power.

How do I calculate the p-value for Pearson correlation in Excel?

Excel's CORREL function only calculates the correlation coefficient, not the p-value. To get the p-value, you need to use the Data Analysis Toolpak's Correlation tool (which also doesn't provide p-values directly), or manually calculate it using the T.DIST function with the formula: t = r × sqrt((n-2)/(1-r²)), where r is the correlation coefficient and n is the sample size.

What does a correlation of 0.9 mean?

A correlation of 0.9 indicates a very strong positive linear relationship between two variables. This means that as one variable increases, the other variable tends to increase at a very consistent rate. However, remember that even a 0.9 correlation means only 81% (0.9²) of the variance in one variable can be explained by the other variable - there's still 19% unexplained variance.

Wrapping Up

The Pearson correlation coefficient is a useful tool for understanding the relationship between two variables, and it is easy to calculate in Excel using either the Data Analysis Toolpak or the CORREL function.