Formula Deviației Standard: Populație vs Eșantion - Ghid Complet (2026)

•By Leonard Cucos•ro
Descriptive StatisticsStatistical Tests

Deviația standard măsoară dispersia scorurilor într-un set de date față de medie. Formula deviației standard pentru populație (σ) împarte suma pătratelor diferențelor la N, în timp ce formula deviației standard pentru eșantion (s) împarte la N-1 (corecția lui Bessel). Diferența cheie: σ folosește μ (media populației) și N, pe când s folosește x̄ (media eșantionului) și N-1 pentru a corecta distorsiunea în estimarea parametrilor populației din datele eșantionului.

În această lecție, vom compara formula deviației standard pentru populație vs. eșantion și cum să calculăm ecuațiile manual.

Deviația standard necesită să cunoaștem media (average) pentru populația sau eșantionul pe care îl măsurăm. Vom demonstra cum să calculăm media pentru un set de valori folosind exemple pas cu pas.

Această lecție demonstrează, de asemenea, cum să calculezi varianța pornind de la deviația standard folosind o relație matematică simplă.

Ce Este Deviația Standard? Definiție și Explicație

Deviația standard măsoară cât de dispersate sunt scorurile într-un set de date în raport cu media scorurilor. Cu alte cuvinte, deviația standard măsoară răspândirea unui grup de puncte de date în raport cu media. Cu cât sunt mai răspândite, cu atât deviația standard este mai mare. Deviația standard este o componentă fundamentală în multe proceduri statistice, inclusiv analiza de corelație și testarea ipotezelor.

Pentru a ne asigura că înțelegem acest concept, gândește-te la următoarele două grupuri de numere: 2, 3, 4 și 2, 4, 6.

Care set de numere are o deviație standard mai mare?

Ai ghicit corect: al doilea grup format din numerele 2, 4 și 6. Dar de ce? Să comparăm aceste grupuri folosind o linie numerică.

Linie numerică arătând distribuția valorilor 2, 3, 4 și 2, 4, 6 pentru a ilustra deviația standard Comparație pe linia numerică arătând răspândirea valorilor pentru calculul deviației standard

Deviația standard pentru al doilea grup de numere (2, 4, 6) trebuie să fie mai mare deoarece valorile pe linia numerică sunt mai răspândite. În contrast, numerele din primul grup (2, 3, 4) sunt mai apropiate; prin urmare, deviația standard trebuie să fie mai mică.

Dar cum dovedim că avem dreptate? La urma urmei, un set de date poate avea sute sau chiar mii de valori.

Ei bine, după cum probabil ai ghicit, folosind ecuația deviației standard.

Înainte de a ne apuca să practicăm abilitățile noastre matematice, ține minte că există două ecuații pentru deviația standard:

  • Formula deviației standard pentru populație calculează deviația standard pentru o întreagă populație și necesită să fie cunoscută media populației.
  • Formula deviației standard pentru eșantion este folosită pentru a calcula deviația standard pentru un eșantion dintr-o populație și necesită să fie cunoscută media eșantionului.

Iată o comparație side-by-side între cele două formule, cu diferențele evidențiate în roșu.

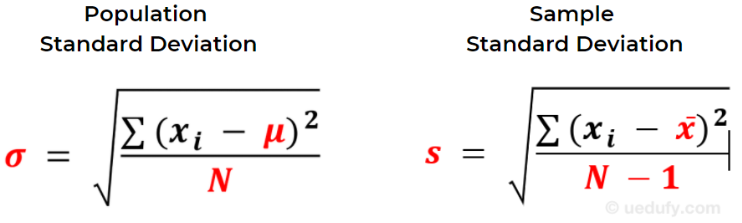Comparație side-by-side a formulelor de deviație standard pentru populație și eșantion cu diferențele evidențiate Comparație între formulele deviației standard pentru populație și eșantion

Simboluri pentru Deviația Standard: Populație vs Eșantion (σ vs s)

Notația diferă între formulele deviației standard pentru populație și eșantion:

Simbolul Deviației Standard pentru Populație:

  • σ (litera greacă mică sigma) = deviația standard a populației
  • μ (litera greacă mică mu) = media populației
  • N = numărul total de valori din populație

Simbolul Deviației Standard pentru Eșantion:

  • s (litera mică s) = deviația standard a eșantionului
  • x̄ (x-bară) = media eșantionului
  • N-1 = dimensiunea eșantionului minus unu (corecția lui Bessel)

Ambele formule calculează deviația standard folosind aceeași abordare fundamentală, cu diferențe cheie în notație și numitor (N vs N-1), pe care le vom demonstra în detaliu în continuare.

Formula Deviației Standard pentru Populație

Așa cum sugerează și numele, următoarea ecuație este folosită pentru a calcula deviația standard pentru o populație dată.

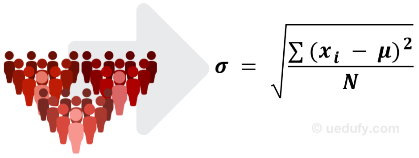Formula deviației standard pentru populație cu simboluri grecești sigma, mu și notație de sumare Formula deviației standard pentru populație

Unde:

  • σ = simbolul pentru deviația standard a populației
  • Σ = suma termenilor următori
  • xi = fiecare punct din setul de date (observație sau membru al populației)
  • μ = media populației
  • N = numărul de valori din populație

Acum să punem totul împreună. Așa citești formula deviației standard pentru populație: deviația standard (σ) este egală cu rădăcina pătrată a sumei (Σ) tuturor diferențelor pătrate între fiecare punct xi din setul de date și media populației (μ), împărțită la toate valorile din set (N).

Următorul, să calculăm deviația standard pentru setul de numere 3, 4 și 5 folosind formula deviației standard pentru populație.

Pasul 1: Găsește media (μ)

Pentru a găsi media tuturor membrilor dintr-o populație, pur și simplu calculează suma tuturor valorilor lor și apoi împarte suma la numărul de valori din setul de date. Iată media pentru setul de numere 3, 4 și 5.

μ=3+4+53=123=4\mu=\frac{3+4+5}{3}=\frac{12}{3}=4

SFAT: Când un set de numere este egal distanțat, media va fi numărul din mijloc. De exemplu, pentru setul de numere 2, 5, 7, 9, 12, media este 7.

Pasul 2: Calculează formula deviației standard pentru populație

σ=∑(xi−μ)2N\sigma=\sqrt{\frac{\sum\left(x_{i}-\mu\right)^{2}}{N}}

Pentru setul de numere 3, 4 și 5, fiecare punct xi = x3, x4, x5, media μ = 4 după cum am calculat mai sus, și populația N = 3 (deoarece avem trei valori în setul de date). Să introducem aceste numere în ecuația deviației standard pentru populație:

σ=(3−4)2+(4−4)2+(5−4)23\sigma=\sqrt{\frac{(3-4)^{2}+(4-4)^{2}+(5-4)^{2}}{3}}

Pasul 3: Calculează suma tuturor punctelor

σ=1+0+13\sigma=\sqrt{\frac{1+0+1}{3}}

Pasul 4: Rezolvă rădăcina pătrată

σ=23=0.66=0.81\sigma=\sqrt{\frac{2}{3}}=\sqrt{0.66}=0.81

Deviația standard pentru populația formată din numerele 3, 4 și 5 este 0.81.

PRACTICĂ: Folosind formula deviației standard pentru populație și urmând exemplul de mai sus, calculează deviația standard pentru setul de numere 2, 4 și 6. Este deviația standard mai mare sau mai mică decât 0.81?

Cu toate acestea, există o problemă importantă cu eșantioanele. În timp ce o medie a populației rămâne aceeași (calculăm întotdeauna media pentru TOȚI membrii populației), un eșantion poate diferi de la unul la altul.

De exemplu, dacă închidem ochii și luăm câteva eșantioane aleatoare constând din 5 numere dintr-un castron cu o sută de numere, fiecare eșantion va conține probabil numere diferite. Prin urmare, mediile eșantioanelor vor diferi, de asemenea, între eșantioane.

Deci cum ne asigurăm că eșantionul pe care îl luăm este reprezentativ pentru populația din care a fost extras? Salută un alt termen statistic numit eroarea standard. Nu vom acoperi eroarea standard deoarece articolul pe care l-am legat mai sus conține tot ce trebuie să știi despre ea.

Formula Deviației Standard pentru Eșantion

Dar ce se întâmplă când nu avem acces la întreaga populație, ci doar la un eșantion din aceasta pentru a calcula media? Acesta este adesea cazul în cercetarea socială și, din fericire pentru noi, formula deviației standard pentru eșantion nu este foarte diferită de cea folosită pentru populație.

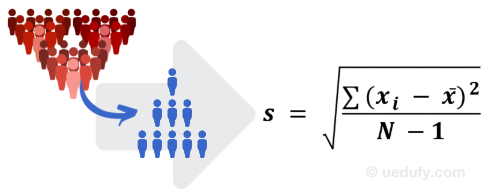Formula deviației standard pentru eșantion cu simbolurile s, x-bară și numitorul N-1 Formula deviației standard pentru eșantion

Unde:

  • s = simbolul pentru deviația standard a eșantionului
  • Σ = suma termenilor următori
  • xi = fiecare punct din setul de date (observație sau membru al populației)
  • x̄ = media eșantionului
  • N-1 = numărul de valori din eșantion (N) minus 1

Și așa citim ecuația de mai sus: deviația standard a eșantionului (s) este egală cu rădăcina pătrată a sumei (Σ) diferențelor pătrate între fiecare punct de date (xi) din eșantion și media eșantionului (x̄), împărțită la populația N – 1.

Diferența este ușor de observat între formulele deviației standard pentru populație și eșantion. O diferență evidentă este notația pentru media eșantionului x̄, spre deosebire de media populației μ. O altă diferență este că împărțim totul la N – 1.

Matematica pentru deviația standard a eșantionului este aproape aceeași, dar să o facem oricum. De data aceasta vom folosi al doilea set de valori de pe linia noastră numerică: 2, 4 și 6.

Pasul 1: Calculează media eșantionului (x̄)

Acest pas este aproape același ca și găsirea mediei populației în exemplul anterior. Media eșantionului pentru setul de numere 2, 4 și 6 este 4. Iată dovada:

xˉ=2+4+63=123=4\bar{x}=\frac{2+4+6}{3}=\frac{12}{3}=4

Pasul 2: Calculează formula deviației standard pentru eșantion

s=∑(xi−xˉ)2N−1s=\sqrt{\frac{\sum\left(x_{i}-\bar{x}\right)^{2}}{N-1}}

Următorul, introdu valorile în ecuația deviației standard pentru eșantion:

s=(2−4)2+(4−4)2+(6−4)23−1s=\sqrt{\frac{(2-4)^{2}+(4-4)^{2}+(6-4)^{2}}{3-1}}

Pasul 3: Rezolvă rădăcina pătrată

s=4+0+42=4=2s=\sqrt{\frac{4+0+4}{2}}=\sqrt{4}=2

Deviația standard pentru eșantionul format din numerele 2, 4 și 6 este 2.

PRACTICĂ:

Folosind formula deviației standard pentru eșantion și urmând exemplul de mai sus, calculează deviația standard pentru setul de numere 2, 5, 7, 9 și 12. Pentru a-ți fi mai ușor, media este 7.

Când Să Folosești Deviația Standard pentru Populație vs Eșantion

Alegerea între deviația standard pentru populație și eșantion depinde de setul tău de date:

Folosește Deviația Standard pentru Populație (σ) când:

  • Ai date pentru fiecare membru al populației
  • Analizezi un set de date complet, finit
  • Vrei să descrii variabilitatea reală a întregului tău set de date
  • Exemplu: Scoruri la teste pentru toți elevii dintr-o singură clasă

Folosește Deviația Standard pentru Eșantion (s) când:

  • Lucrezi cu un subset dintr-o populație mai mare
  • Vrei să estimezi parametrii populației din datele eșantionului
  • Desfășori cercetări unde colectarea tuturor datelor populației este impractică
  • Exemplu: Răspunsuri la un sondaj de la 500 de persoane pentru a estima opiniile a 50.000 de rezidenți

În cercetare și statistică, deviația standard pentru eșantion este mult mai comună deoarece accesul la populații întregi este rareori fezabil. Numitorul N-1 din formula pentru eșantion oferă o estimare nedistorsionată a deviației standard a populației. Pentru calcule practice, poți folosi funcțiile încorporate în Excel pentru a calcula automat atât deviația standard pentru populație, cât și pentru eșantion.

Cum Să Calculezi Varianța pornind de la Deviația Standard

Deviația standard și varianța sunt măsuri strâns legate de dispersie. În timp ce deviația standard arată cât de dispersate sunt valorile față de medie, varianța reprezintă distanța pătrată medie a fiecărui punct față de medie. Varianța este fundamentală pentru multe teste statistice, inclusiv ANOVA și analiza de regresie.

Relația dintre deviația standard și varianță devine clară când privim cum este calculată varianța. Dacă știm deviația standard pentru populație sau eșantion, tot ce trebuie să facem este să o ridicăm la pătrat pentru a găsi varianța.

σ2=∑(xi−μ)2N\sigma^{2}={\frac{\sum\left(x_{i}-\mu\right)^{2}}{N}}

De exemplu, rezultatul deviației standard pentru populație pe care l-am calculat mai devreme este σ = 0.81, deci putem calcula varianța populației din aceasta: 0.81² = 0.6561. Varianța pentru setul de numere 3, 4 și 5 este 0.6561.

Același lucru poate fi făcut pentru a calcula varianța pentru eșantion folosind următoarea ecuație:

s2=∑(xi−xˉ)2N−1s^{2}={\frac{\sum\left(x_{i}-\bar{x}\right)^{2}}{N-1}}

Deci, pentru a găsi varianța pentru eșantionul pe care l-am calculat mai devreme, tot ce avem nevoie este să ridicăm la pătrat deviația standard a eșantionului, respectiv: s² = 2² = 4. Pentru implementări în Excel, consultă ghidul nostru despre cum să calculezi deviația standard cu Excel atât pentru populație, cât și pentru eșantion.

Întrebări Frecvente Despre Deviația Standard pentru Populație și Eșantion

Deviația standard pentru populație (σ) calculează variabilitatea pentru o întreagă populație împărțind la N, în timp ce deviația standard pentru eșantion (s) estimează variabilitatea populației dintr-un eșantion împărțind la N-1. Numitorul N-1 corectează distorsiunea atunci când se estimează parametrii populației din datele eșantionului.
Folosește deviația standard pentru populație când ai date pentru fiecare membru al populației. Folosește deviația standard pentru eșantion când lucrezi cu un subset al populației pentru a estima parametrii populației. În cercetare, deviația standard pentru eșantion este cea mai comună deoarece colectarea datelor de la populații întregi este rareori fezabilă.
Simbolul pentru deviația standard a populației este litera greacă sigma (σ). Media populației este reprezentată de mu (μ), iar N reprezintă numărul total de valori din populație.
Simbolul pentru deviația standard a eșantionului este litera mică s. Media eșantionului este reprezentată de x̄ (x-bară), iar numitorul folosește N-1 în loc de N pentru a corecta distorsiunea eșantionului.
Împărțirea la N-1 în loc de N oferă o estimare nedistorsionată a deviației standard a populației din datele eșantionului. Această corecție, cunoscută sub numele de corecția lui Bessel, ține cont de faptul că datele eșantionului tind să subestimeze variabilitatea populației. Ajustarea N-1 crește ușor deviația standard calculată pentru a aproxima mai bine valoarea reală a populației.
Varianța este egală cu deviația standard la pătrat. Pentru varianța populației: σ² = (deviația standard)². Pentru varianța eșantionului: s² = (deviația standard)². Invers, deviația standard este egală cu rădăcina pătrată a varianței.

Concluzie

Înțelegerea distincției dintre deviația standard pentru populație și eșantion este fundamentală pentru analiza statistică. Deviația standard pentru populație (σ) se aplică atunci când se analizează seturi de date complete, în timp ce deviația standard pentru eșantion (s) este folosită atunci când se lucrează cu subseturi pentru a estima parametrii populației.

Diferențele cheie constau în notație și metoda de calcul. Deviația standard pentru populație folosește μ pentru medie și împarte la N, în timp ce deviația standard pentru eșantion folosește x̄ și împarte la N-1 pentru a corecta distorsiunea de estimare. Această ajustare N-1, cunoscută sub numele de corecția lui Bessel, asigură că statisticile eșantionului oferă estimări nedistorsionate ale parametrilor populației.

Ambele formule măsoară variabilitatea calculând rădăcina pătrată a mediei pătratelor abaterilor de la medie. Varianța, valoarea pătratică a deviației standard, oferă o măsură alternativă de dispersie utilizată pe scară largă în analiza fiabilității, cum ar fi Cronbach's Alpha și alte evaluări psihometrice.

Referințe

Diez D.M., Cetinkaya-Rundel M., Barr C.D. (2019). OpenIntro: Statistics (4th Ed).

Field, A. (2018). Discovering statistics using IBM SPSS statistics (5th edition). Sage: Thousand Oaks, CA.