Standard Deviation în Excel: Funcțiile STDEV.S, STDEV.P și Formule

•By Leonard Cucos•ro
Descriptive StatisticsExcelStatistical Tests

Calcularea Standard Deviation în Excel este esențială pentru măsurarea variabilității și dispersiei datelor. Excel oferă multiple funcții pentru Standard Deviation: STDEV.S pentru datele de eșantion (cel mai comun), STDEV.P pentru datele populației și funcții legacy STDEV/STDEVP. Acest ghid complet acoperă toate formulele Excel pentru Standard Deviation, când să folosești fiecare funcție și exemple pas cu pas cu interpretări.

Folosește =STDEV.S(range) pentru Standard Deviation al eșantionului sau =STDEV.P(range) pentru Standard Deviation al populației. Descarcă fișierul Excel pentru practică din bara laterală pentru a urma exemplele reale.

Referință Rapidă: Formule Excel pentru Standard Deviation

FuncțieFolosit pentruSintaxăExemplu
STDEV.SSample (cel mai folosit)=STDEV.S(range)=STDEV.S(A2:A50)
STDEV.PPopulation=STDEV.P(range)=STDEV.P(A2:A50)
STDEVASample + valori logice=STDEVA(range)=STDEVA(A2:A50)
STDEVPAPopulation + valori logice=STDEVPA(range)=STDEVPA(A2:A50)
Funcții Excel pentru calcularea Standard Deviation

Folosește STDEV.S în 95% din cazuri - este alegerea corectă când lucrezi cu date de eșantion dintr-o populație mai mare.

Dacă nu ești sigur despre diferența dintre Standard Deviation al populației și eșantionului, citește mai întâi acel ghid pentru a înțelege care formulă se aplică datelor tale.

Înțelegerea Formulelor Standard Deviation

Standard Deviation măsoară cât de mult valorile individuale deviază de la medie. Două formule diferite sunt folosite în funcție de dacă datele tale reprezintă:

  • Sample (n) - Un subset al unei populații mai mari
  • Population (N) - Întregul grup pe care îl studiezi

Formula Standard Deviation al Populației

Standard Deviation al populației (σ) este folosit când ai date pentru întreaga populație:

σ=∑(xi−μ)2N\Large \sigma = \sqrt{\frac{\sum(x_i - \mu)^2}{N}}

Unde:

  • σ = Standard Deviation al populației
  • Σ = suma termenilor următori
  • xi = fiecare valoare din setul de date
  • μ = media populației
  • N = numărul total de valori în populație

Formula Standard Deviation al Eșantionului

Standard Deviation al eșantionului (s) este folosit când ai date dintr-un eșantion al unei populații mai mari:

s=∑(xi−xˉ)2n−1\Large s = \sqrt{\frac{\sum(x_i - \bar{x})^2}{n-1}}

Unde:

  • s = Standard Deviation al eșantionului
  • Σ = suma termenilor următori
  • xi = fiecare valoare din eșantion
  • x̄ = media eșantionului
  • n-1 = gradele de libertate (corecția Bessel)

Diferența cheie este împărțirea la n-1 în loc de N pentru a corecta bias-ul când estimăm parametrii populației din datele de eșantion.

Cum să Calculezi Standard Deviation al Populației în Excel

Excel oferă două funcții pentru calcularea Standard Deviation al populației:

Funcția STDEV.P

Funcția STDEV.P calculează Standard Deviation al populației și ignoră automat textul și valorile logice (TRUE/FALSE).

Sintaxă:

=STDEV.P(number1, [number2], ...)

Exemplu:

Să presupunem că ai date pentru o întreagă populație în celulele C2:C11. Iată cum să calculezi Standard Deviation al populației pas cu pas:

Pasul 1: Accesează dialogul Insert Function dând click pe butonul "fx" sau apăsând Shift+F3.

Pasul 2: Tastează "STDEV.P" în câmpul de căutare și dă click pe Go, apoi selectează STDEV.P din listă:

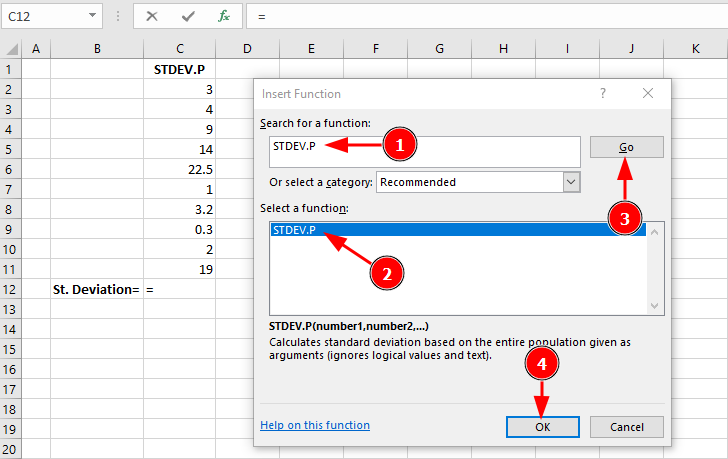
Dialogul Excel Insert Function arătând selecția funcției STDEV.P cu câmpul de căutare și descrierea funcției

Căutarea și selectarea funcției STDEV.P în Excel

Pasul 3: În dialogul Function Arguments, selectează intervalul de date (C2:C11):

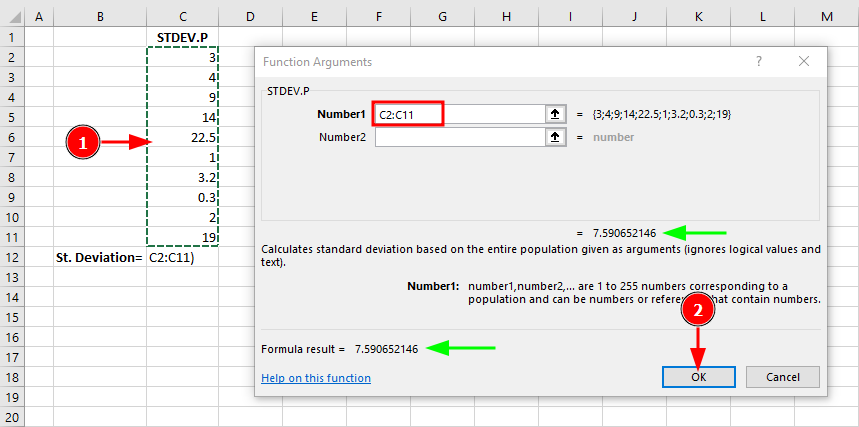
Dialogul Excel Function Arguments pentru STDEV.P arătând intervalul de date C2:C11 și rezultatul calculat de 7.59

Dialogul Function Arguments pentru STDEV.P cu intervalul de date și rezultatul

Pasul 4: Dă click pe OK pentru a vedea rezultatul final:

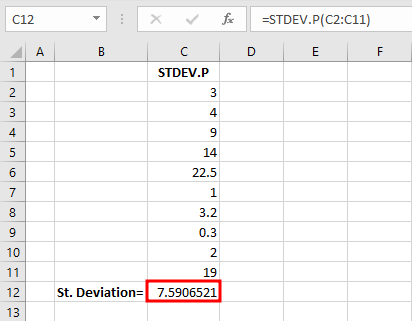
Foaie de calcul Excel arătând rezultatul formulei STDEV.P de 7.59 în celula C12

Calculul STDEV.P completat arătând Standard Deviation al populației

Funcția returnează 7.59 ca Standard Deviation al populației, arătând cât de dispersate sunt valorile față de medie.

Funcția STDEVPA

Funcția STDEVPA calculează de asemenea Standard Deviation al populației dar include textul și valorile logice:

  • Text și FALSE = 0
  • TRUE = 1

Sintaxă:

=STDEVPA(value1, [value2], ...)

Exemplu:

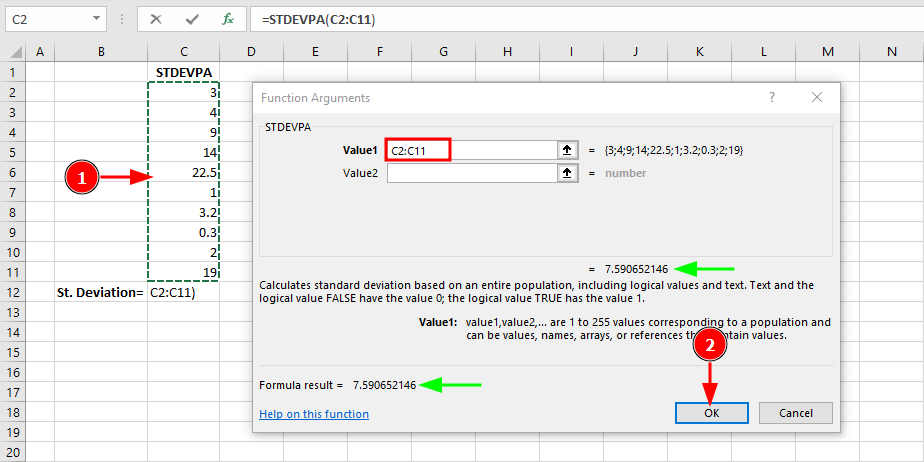
Dialogul Excel Function Arguments pentru STDEVPA arătând intervalul de date și rezultatul de 7.59, cu descriere notând că include valori logice

Funcția STDEVPA include valorile logice și textul în calcul

Folosește STDEVPA când setul tău de date include intenționat valori logice pe care vrei să le incluzi în calcul. În acest exemplu, deoarece setul de date conține doar numere, STDEVPA returnează același rezultat ca STDEV.P (7.59).

Cum să Calculezi Standard Deviation al Eșantionului în Excel

Pentru majoritatea scenariilor din lumea reală, lucrezi cu un eșantion (nu întreaga populație). Excel oferă două funcții pentru Standard Deviation al eșantionului:

Funcția STDEV.S (Cea Mai Folosită)

Funcția STDEV.S calculează Standard Deviation al eșantionului și este funcția cea mai folosită în mod obișnuit. Ignoră textul și valorile logice.

Sintaxă:

=STDEV.S(number1, [number2], ...)

Exemplu:

Iată cum să calculezi Standard Deviation al eșantionului folosind același set de date (C2:C11), care acum reprezintă un eșantion dintr-o populație mai mare:

Pasul 1: Accesează dialogul Insert Function și caută "STDEV.S":

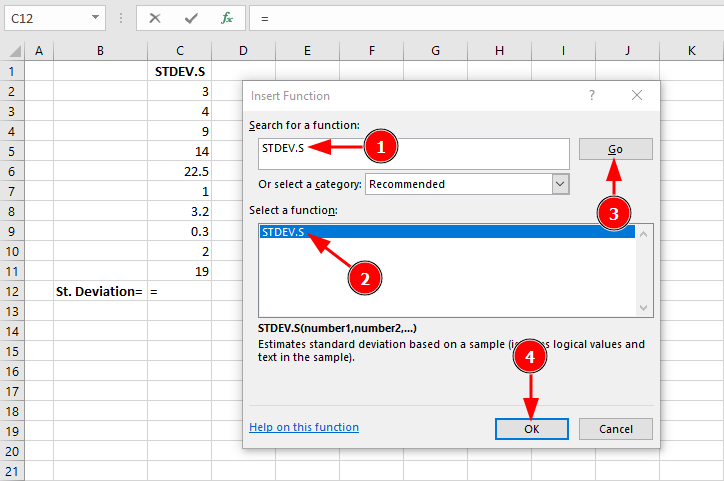
Dialogul Excel Insert Function arătând selecția funcției STDEV.S cu descriere despre Standard Deviation al eșantionului

Selectarea funcției STDEV.S pentru Standard Deviation al eșantionului

Pasul 2: În dialogul Function Arguments, selectează intervalul de date:

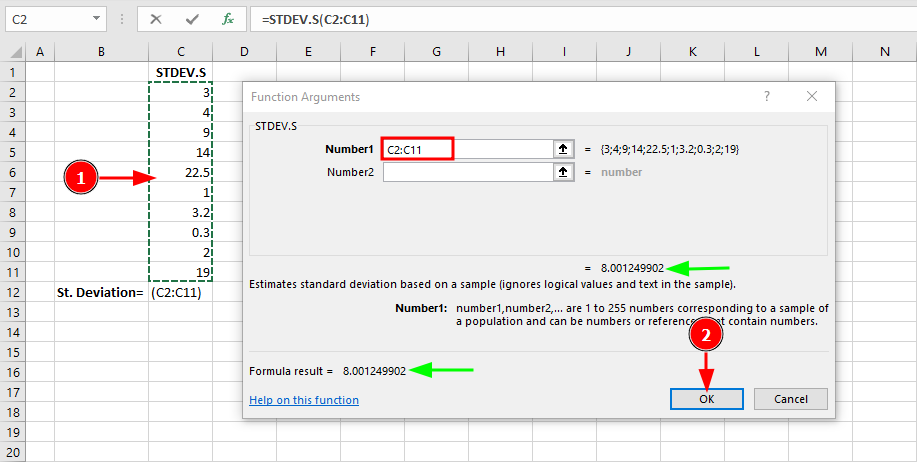
Dialogul Excel Function Arguments pentru STDEV.S arătând intervalul de date C2:C11 și rezultatul de 8.00

STDEV.S returnează 8.00 (mai mare decât STDEV.P datorită corecției Bessel n-1)

Observă că rezultatul este 8.00 pentru Standard Deviation al eșantionului, comparat cu 7.59 pentru Standard Deviation al populației. Această diferență se datorează corecției Bessel (împărțire la n-1 în loc de N), care oferă o estimare nebiasată când lucrezi cu date de eșantion.

Aceasta este alegerea implicită pentru majoritatea analizelor statistice când lucrezi cu date de eșantion.

Funcția STDEVA

Funcția STDEVA calculează Standard Deviation al eșantionului dar include textul și valorile logice:

  • Text și FALSE = 0
  • TRUE = 1

Sintaxă:

=STDEVA(value1, [value2], ...)

Exemplu:

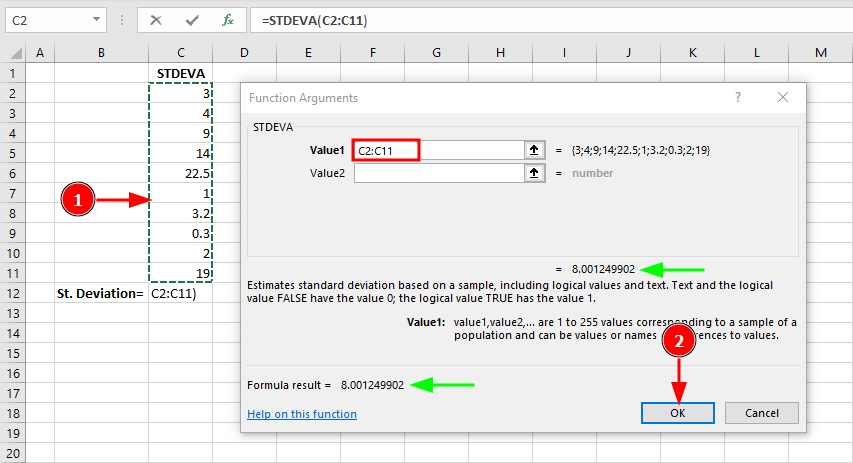
Dialogul Excel Function Arguments pentru STDEVA arătând intervalul de date și rezultatul de 8.00, cu descriere despre includerea valorilor logice

Funcția STDEVA include valorile logice și textul în calculul Standard Deviation al eșantionului

Folosește STDEVA doar când ai nevoie specific să incluzi valori logice în calculul tău. În acest exemplu cu date pur numerice, STDEVA returnează același rezultat ca STDEV.S (8.00).

Funcții Legacy pentru Standard Deviation

Excel include de asemenea funcții mai vechi pentru compatibilitate inversă:

Funcție LegacyEchivalent ModernCaz de Utilizare
STDEVSTDEV.SStandard Deviation al eșantionului
STDEVPSTDEV.PStandard Deviation al populației
Funcții legacy vs moderne pentru Standard Deviation

Recomandare: Folosește întotdeauna funcțiile moderne (STDEV.S, STDEV.P) deoarece sunt mai explicite despre dacă calculezi Standard Deviation al eșantionului sau populației.

Ce Funcție Standard Deviation Ar Trebui să Folosești?

Iată un ghid rapid de decizie:

Folosește STDEV.S când:

  • Lucrezi cu un eșantion dintr-o populație mai mare (cazul cel mai comun)
  • Conduci sondaje, experimente sau studii de eșantionare
  • Ai un subset de date reprezentând un grup mai mare
  • Exemplu: Scoruri de test de la 30 de studenți din 500 de studenți totali

Folosește STDEV.P când:

  • Ai date pentru întreaga populație
  • Setul tău de date include fiecare singur membru al grupului
  • Exemplu: Scoruri de test pentru toți cei 30 de studenți dintr-o clasă completă

Folosește STDEVPA/STDEVA când:

  • Setul tău de date include intenționat valori TRUE/FALSE sau text
  • Vrei ca aceste valori să fie numărate ca 1 și 0 respectiv

Regulă generală: Dacă nu ești sigur, folosește STDEV.S (eșantion). Este alegerea statistic conservatoare și potrivită pentru majoritatea analizelor.

Interpretarea Rezultatelor Standard Deviation

Înțelegerea ce înseamnă valoarea ta de Standard Deviation:

Standard Deviation Mic (aproape de 0):

  • Punctele de date se grupează strâns în jurul mediei
  • Variabilitate redusă
  • Valorile sunt consistente și previzibile
  • Exemplu: SD = 2 pentru scoruri de test cu media 85 înseamnă că majoritatea scorurilor sunt între 83-87

Standard Deviation Mare:

  • Punctele de date sunt dispersate de la medie
  • Variabilitate ridicată
  • Valorile sunt mai puțin consistente
  • Exemplu: SD = 15 pentru scoruri de test cu media 85 înseamnă că scorurile variază foarte mult (70-100)

Într-o distribuție normală:

  • ~68% din valori se încadrează într-un Standard Deviation de la medie
  • ~95% din valori se încadrează în 2 Standard Deviation
  • ~99.7% din valori se încadrează în 3 Standard Deviation

Pentru mai multe despre măsurile de tendință centrală și dispersie, vezi ghidul nostru despre calcularea mediei, medianei și modului.

Greșeli Comune de Evitat

1. Folosirea STDEV.P pentru date de eșantion

  • Aceasta subestimează variabilitatea în eșantionul tău
  • Folosește întotdeauna STDEV.S când lucrezi cu eșantioane

2. Includerea antetelor în intervalul tău

  • STDEV.S va returna o eroare dacă antetele text sunt incluse
  • Selectează doar celulele cu date numerice

3. Amestecarea formulelor de eșantion și populație

  • Fii consistent: datele de eșantion necesită formule de eșantion în toată analiza ta

4. Ignorarea valorilor extreme (outliers)

  • Valorile extreme afectează semnificativ Standard Deviation
  • Ia în considerare eliminarea outliers sau folosirea medianei/IQR pentru date asimetrice

Întrebări Frecvente

STDEV.S calculează Standard Deviation al eșantionului (împărțind la n-1) și este folosit când datele tale sunt un eșantion dintr-o populație mai mare. STDEV.P calculează Standard Deviation al populației (împărțind la N) și este folosit când ai date pentru întreaga populație. Folosește STDEV.S pentru majoritatea scenariilor din lumea reală unde lucrezi cu date de eșantion.
Folosește Standard Deviation al eșantionului (STDEV.S) când datele tale reprezintă un subset al unui grup mai mare pe care încerci să-l înțelegi. Folosește Standard Deviation al populației (STDEV.P) doar când ai fiecare singur punct de date din populația completă. De exemplu: sondarea a 100 de clienți din 10.000 = eșantion. Înregistrarea scorurilor de test pentru toți cei 30 de studenți din clasa ta completă = populație.
Un Standard Deviation de 0 înseamnă că nu există variabilitate în datele tale—toate valorile sunt exact aceleași. De exemplu, dacă toate scorurile de test sunt 85, Standard Deviation este 0. Acest lucru este rar în datele reale și indică adesea o eroare de introducere a datelor sau că măsori o constantă.
Nu, Standard Deviation nu poate fi niciodată negativ. Este calculat ca o rădăcină pătrată a varianței (care este întotdeauna pozitivă sau zero), deci rezultatul este întotdeauna zero sau pozitiv. Dacă Excel returnează o valoare negativă, există o eroare în formula sau datele tale.
Poți calcula Standard Deviation pentru fiecare coloană separat folosind STDEV.S pe fiecare interval: =STDEV.S(A2:A50) pentru coloana A, =STDEV.S(B2:B50) pentru coloana B etc. Excel nu are o funcție încorporată pentru a calcula Standard Deviation pe multiple coloane non-adiacente într-o singură formulă.
Corecția Bessel este împărțirea la (n-1) în loc de n când calculezi Standard Deviation al eșantionului. Această corecție compensează bias-ul introdus când estimăm parametrii populației din datele de eșantion. Oferă o estimare mai precisă (nebiasată) a adevăratului Standard Deviation al populației. STDEV.S folosește această corecție automat.
Pentru datele grupate cu frecvențe, înmulțește fiecare valoare cu frecvența sa, apoi folosește formule array sau creează un set de date extins. De exemplu, dacă valoarea 10 apare de 5 ori, fie o listezi de 5 ori fie folosești: =SQRT(SUMPRODUCT((values-AVERAGE(values))^2, frequencies)/SUM(frequencies)) pentru populație sau împarte la (SUM(frequencies)-1) pentru eșantion.

Concluzie

Calcularea Standard Deviation în Excel este simplă odată ce înțelegi ce funcție să folosești. Pentru majoritatea analizelor care implică date de eșantion, STDEV.S este funcția ta de bază, în timp ce STDEV.P este rezervată pentru seturi de date complete ale populației.

Înțelegerea Standard Deviation este crucială pentru analiza variabilității în datele tale și formează fundamentul pentru analize statistice mai avansate. Combinat cu media, mediana și modul, Standard Deviation îți oferă o imagine completă a distribuției datelor tale.

Practică cu fișierul Excel descărcabil pentru a construi încredere în calcularea și interpretarea Standard Deviation pentru propriile tale seturi de date.