Stratified Sampling คืออะไร? วิธีการสุ่มตัวอย่างแบบแบ่งชั้น ขั้นตอน และตัวอย่าง

Stratified Sampling เป็นเทคนิคการสุ่มตัวอย่างแบบความน่าจะเป็นที่ผู้วิจัยแบ่งประชากรออกเป็นกลุ่มย่อยที่แตกต่างกัน (เรียกว่า Strata) ตามลักษณะที่มีร่วมกัน จากนั้นจึงสุ่มเลือกตัวอย่างจากแต่ละ Stratum อย่างสัดส่วน วิธีการนี้ช่วยให้มั่นใจว่ากลุ่มย่อยเฉพาะจะได้รับการเป็นตัวแทนอย่างเพียงพอในกลุ่มตัวอย่างสุดท้าย ทำให้มีคุณค่าอย่างยิ่งเมื่อศึกษาประชากรที่หลากหลาย

คู่มือนี้อธิบายว่า Stratified Sampling คืออะไร แตกต่างจากวิธีการสุ่มตัวอย่างอื่นอย่างไร ขั้นตอนการดำเนินการทีละขั้นตอน ตัวอย่างจากโลกจริง และเมื่อไหร่ควรใช้เทคนิคนี้ในงานวิจัยของคุณ

Stratified Sampling คืออะไร?

Stratified Sampling (เรียกอีกชื่อว่า Stratified Random Sampling) เป็นวิธีการสุ่มตัวอย่างแบบความน่าจะเป็นที่แบ่งประชากรออกเป็นกลุ่มย่อยที่เป็นเนื้อเดียวกัน (Strata) ตามลักษณะเฉพาะ จากนั้นจึงสุ่มเลือกตัวอย่างจากแต่ละ Stratum หลักการสำคัญคือทุกสมาชิกของประชากรต้องอยู่ใน Stratum ใดStratum หนึ่งเท่านั้น และกลุ่มตัวอย่างต้องมีสัดส่วนเดียวกับประชากรเดิม

องค์ประกอบสำคัญ

Strata: กลุ่มย่อยที่แตกต่างและไม่ทับซ้อนกันภายในประชากร ซึ่งกำหนดโดยลักษณะที่มีร่วมกัน สมาชิกแต่ละคนของประชากรอยู่ใน Stratum เดียวเท่านั้น

การเป็นตัวแทนตามสัดส่วน: องค์ประกอบของกลุ่มตัวอย่างสะท้อนโครงสร้างของประชากร หากกลุ่ม A คิดเป็น 30% ของประชากร กลุ่มตัวอย่างของคุณก็ควรมีกลุ่ม A 30% เช่นกัน

การเลือกแบบสุ่มภายใน Strata: หลังจากแบ่งประชากรเป็น Strata แล้ว ผู้วิจัยใช้เทคนิค Random Sampling (เช่น Simple Random Sampling) ภายในแต่ละ Stratum เพื่อเลือกผู้เข้าร่วม

Stratified Sampling ทำงานอย่างไร

กระบวนการพื้นฐานประกอบด้วย 3 ขั้นตอน:

1. แบ่ง ประชากรออกเป็น Strata ที่แยกจากกันโดยสิ้นเชิง ตามลักษณะที่เกี่ยวข้อง
2. กำหนด ขนาดกลุ่มตัวอย่างสำหรับแต่ละ Stratum (การจัดสรรแบบสัดส่วนหรือไม่สัดส่วน)
3. สุ่มเลือก ผู้เข้าร่วมจำนวนที่กำหนดจากแต่ละ Stratum

วิธีการนี้ผสมผสานข้อดีของการสุ่มตัวอย่างแบบควบคุม (ผ่านการแบ่งชั้น) กับความถูกต้องทางสถิติของการเลือกแบบสุ่ม (ภายในแต่ละ Stratum)

Stratified Sampling เทียบกับวิธีการสุ่มตัวอย่างอื่น

การเข้าใจว่า Stratified Sampling แตกต่างจากเทคนิคการสุ่มตัวอย่างแบบความน่าจะเป็นอื่นอย่างไร จะช่วยให้คุณเลือกวิธีการที่เหมาะสมสำหรับงานวิจัยของคุณ

Stratified Sampling เทียบกับ Simple Random Sampling

Simple Random Sampling เลือกผู้เข้าร่วมแบบสุ่มจากประชากรทั้งหมดโดยไม่แบ่งออกเป็นกลุ่ม ทุกคนมีโอกาสถูกเลือกเท่ากัน

ความแตกต่าง: Stratified Sampling รับประกันการเป็นตัวแทนของกลุ่มย่อยเฉพาะ ในขณะที่ Simple Random Sampling อาจทำให้บางกลุ่มมีตัวแทนน้อยเกินไปหรือมากเกินไปโดยบังเอิญ

ตัวอย่าง: หากประชากรของคุณมีเพศชาย 70% และเพศหญิง 30% Simple Random Sampling อาจสร้างกลุ่มตัวอย่างที่เป็นเพศชาย 80% และเพศหญิง 20% แต่ Stratified Sampling จะรับรองว่ากลุ่มตัวอย่างมีสัดส่วน 70/30

การเป็นตัวแทนตามสัดส่วนใน Stratified Sampling - รักษาสัดส่วนเพศเดียวกันจากประชากรสู่กลุ่มตัวอย่าง

เมื่อไหร่ควรเลือก Stratified แทน Simple Random: ใช้ Stratified Sampling เมื่อคุณต้องการให้แน่ใจว่ากลุ่มย่อยเฉพาะได้รับการเป็นตัวแทนตามสัดส่วน โดยเฉพาะเมื่อศึกษาประชากรที่หลากหลายซึ่งมีความแตกต่างเชิงหมวดหมู่ที่สำคัญ

Stratified Sampling เทียบกับ Cluster Sampling

Cluster Sampling แบ่งประชากรออกเป็นกลุ่ม (Clusters เช่น พื้นที่ทางภูมิศาสตร์หรือโรงเรียน) จากนั้นสุ่มเลือกทั้ง Clusters และสำรวจสมาชิกทั้งหมดภายใน Clusters ที่เลือก

ความแตกต่าง: Stratified Sampling เลือกบางคนจากทุก Stratum ในขณะที่ Cluster Sampling เลือกทุกคนจากบาง Clusters และไม่เลือกจาก Clusters อื่น

ตัวอย่าง:

• Stratified: แบ่งนักเรียนตามระดับชั้น (ม.1, ม.2, ม.3, ม.4) จากนั้นสุ่มเลือกนักเรียน 50 คนจากแต่ละระดับชั้น
• Cluster: สุ่มเลือก 5 โรงเรียนจาก 20 โรงเรียน จากนั้นสำรวจนักเรียนทั้งหมดใน 5 โรงเรียนนั้น

เมื่อไหร่ควรเลือก Stratified แทน Cluster: ใช้ Stratified Sampling เมื่อคุณสามารถเข้าถึงประชากรทั้งหมดและต้องการให้แน่ใจว่าทุกกลุ่มย่อยได้รับการเป็นตัวแทน ใช้ Cluster Sampling เมื่อข้อจำกัดทางภูมิศาสตร์หรือโลจิสติกส์ทำให้การสุ่มตัวอย่างทั่วทั้งประชากรเป็นไปไม่ได้

Stratified Sampling เทียบกับ Systematic Sampling

Systematic Sampling เลือกบุคคลที่ n ทุกคนจากรายชื่อของประชากร (เช่น ทุกคนที่ 10)

ความแตกต่าง: Stratified Sampling รับประกันการเป็นตัวแทนของกลุ่มย่อยอย่างจงใจผ่านการจัดกลุ่ม ในขณะที่ Systematic Sampling พึ่งพาลำดับในรายชื่อและช่วงการสุ่มตัวอย่าง

เมื่อไหร่ควรเลือก Stratified แทน Systematic: ใช้ Stratified Sampling เมื่อองค์ประกอบของประชากรมีความสำคัญและคุณต้องการรับประกันการเป็นตัวแทนของกลุ่มเฉพาะ ใช้ Systematic Sampling เมื่อคุณมีรายชื่อที่สมบูรณ์และลักษณะของประชากรกระจายอย่างสม่ำเสมอ

ขั้นตอนการดำเนินการ Stratified Sampling

ปฏิบัติตามขั้นตอนอย่างเป็นระบบนี้เพื่อนำ Stratified Sampling ไปใช้ในงานวิจัยของคุณ

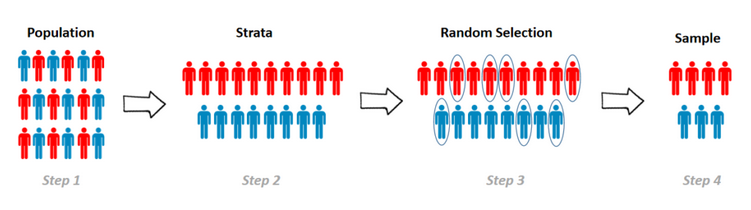
กระบวนการ Stratified Sampling - แบ่งประชากรเป็นชั้น จากนั้นเลือกแบบสุ่มจากแต่ละชั้น

ขั้นตอนที่ 1: กำหนดประชากรของคุณ

ระบุกลุ่มทั้งหมดที่คุณต้องการศึกษาอย่างชัดเจน ประชากรควรเกี่ยวข้องกับคำถามวิจัยของคุณและมีคำจำกัดความที่ชัดเจนด้วยเกณฑ์การรวมและการยกเว้นเฉพาะ

ตัวอย่าง: หากวิจัยเรื่องความพึงพอใจของพนักงานในบริษัท ประชากรของคุณอาจเป็น "พนักงานเต็มเวลาทั้งหมดที่ทำงานในบริษัทอย่างน้อย 6 เดือนตั้งแต่วันที่ 1 มกราคม 2025"

ข้อควรพิจารณาที่สำคัญ:

• กำหนดขอบเขตอย่างชัดเจน (ใครรวมอยู่ด้วยและใครไม่รวม)
• ตรวจสอบว่าคุณสามารถเข้าถึงรายชื่อสมาชิกประชากรที่สมบูรณ์
• กำหนดขนาดประชากรทั้งหมด (N)

ขั้นตอนที่ 2: ระบุตัวแปรการแบ่งชั้น

เลือกลักษณะที่จะกำหนด Strata ของคุณ ตัวแปรนี้ควรเป็น:

• เกี่ยวข้อง กับคำถามวิจัยของคุณ
• เชิงหมวดหมู่ (ไม่ใช่ต่อเนื่อง)
• ครอบคลุมทั้งหมด (สมาชิกประชากรทุกคนเข้ากับหมวดหมู่ใดหมวดหมู่หนึ่ง)
• แยกจากกันโดยเฉพาะ (ไม่มีใครเข้ากับหลายหมวดหมู่)

ตัวแปรการแบ่งชั้นทั่วไป:

• ข้อมูลประชากร: กลุ่มอายุ, เพศ, เชื้อชาติ, ระดับการศึกษา
• ภูมิศาสตร์: ภูมิภาค, รัฐ, เมือง/ชนบท, เขตภูมิอากาศ
• เศรษฐกิจสังคม: ช่วงรายได้, สถานะการจ้างงาน, อาชีพ
• พฤติกรรม: ประเภทลูกค้า, ความถี่ในการใช้ผลิตภัณฑ์, ประวัติการลงคะแนน

ตัวอย่าง: สำหรับการศึกษาความพึงพอใจของพนักงาน คุณอาจแบ่งชั้นตามแผนก (ฝ่ายขาย, วิศวกรรม, การตลาด, HR, ปฏิบัติการ) เพื่อให้แน่ใจว่าเสียงของแต่ละแผนกได้รับการสะท้อนตามสัดส่วน

ขั้นตอนที่ 3: แบ่งประชากรออกเป็น Strata

มอบหมายสมาชิกประชากรแต่ละคนให้อยู่ใน Stratum เดียวตามตัวแปรการแบ่งชั้นที่คุณเลือก

ข้อกำหนด:

• Strata ต้อง แยกจากกันโดยเฉพาะ (ไม่ทับซ้อน)
• Strata ต้อง ครอบคลุมทั้งหมด (ทุกคนเข้ากับที่ไหนสักแห่ง)
• Strata ควร เป็นเนื้อเดียวกันภายใน (สมาชิกมีลักษณะคล้ายกัน)
• Strata ควร แตกต่างกันระหว่าง (Strata ต่างกันมีลักษณะแตกต่างกัน)

ตัวอย่าง: ในบริษัทที่มีพนักงาน 1,000 คน:

• ฝ่ายขาย: 300 คน (30%)
• วิศวกรรม: 400 คน (40%)
• การตลาด: 150 คน (15%)
• HR: 50 คน (5%)
• ปฏิบัติการ: 100 คน (10%)

ขั้นตอนที่ 4: กำหนดขนาดกลุ่มตัวอย่างสำหรับแต่ละ Stratum

คำนวณจำนวนผู้เข้าร่วมที่จะเลือกจากแต่ละ Stratum มีสองวิธีหลัก:

Proportional Stratified Sampling (แนะนำ)

ขนาดกลุ่มตัวอย่างสำหรับแต่ละ Stratum เป็นสัดส่วนตามขนาดของ Stratum นั้นในประชากร วิธีนี้รักษาองค์ประกอบตามธรรมชาติของประชากร

สูตร:

โดยที่:

• $n_h$ = ขนาดกลุ่มตัวอย่างสำหรับ Stratum h
• $N_h$ = ขนาดประชากรของ Stratum h
• $N$ = ขนาดประชากรทั้งหมด
• $n$ = ขนาดกลุ่มตัวอย่างทั้งหมดที่ต้องการ

ตัวอย่าง: หากคุณต้องการกลุ่มตัวอย่างทั้งหมด 200 คนจากพนักงาน 1,000 คน:

• ฝ่ายขาย: (300/1,000) × 200 = 60 คน
• วิศวกรรม: (400/1,000) × 200 = 80 คน
• การตลาด: (150/1,000) × 200 = 30 คน
• HR: (50/1,000) × 200 = 10 คน
• ปฏิบัติการ: (100/1,000) × 200 = 20 คน

Disproportional Stratified Sampling (กรณีพิเศษ)

จงใจสุ่มมากเกินไปหรือน้อยเกินไปในบาง Strata ใช้วิธีนี้เมื่อ:

• Strata ขนาดเล็กต้องการขนาดกลุ่มตัวอย่างที่เพียงพอสำหรับการวิเคราะห์ (อย่างน้อย 30 เพื่อความถูกต้องทางสถิติ)
• คุณต้องการเปรียบเทียบกลุ่มด้วยสถิติกำลัง (Statistical Power) ที่เท่ากัน
• คำถามวิจัยมุ่งเน้นไปที่กลุ่มย่อยเฉพาะ

ตัวอย่าง: เพื่อให้แน่ใจว่า HR มีตัวแทนเพียงพอสำหรับการวิเคราะห์ คุณอาจสุ่มตัวอย่าง 30 คนจาก HR (แทนที่จะเป็น 10) ในขณะที่ปรับ Strata อื่นลง

สำคัญ: เมื่อใช้ Disproportional Sampling คุณต้องใช้การถ่วงน้ำหนักทางสถิติระหว่างการวิเคราะห์เพื่อปรับการเลือกที่ไม่เป็นสัดส่วน

ขั้นตอนที่ 5: สุ่มเลือกผู้เข้าร่วมภายในแต่ละ Stratum

ใช้ Simple Random Sampling ภายในแต่ละ Stratum เพื่อเลือกจำนวนผู้เข้าร่วมที่กำหนด

วิธีการ:

1. การสร้างตัวเลขสุ่ม: กำหนดหมายเลขให้สมาชิกแต่ละคนใน Stratum จากนั้นใช้ตัวสร้างตัวเลขสุ่มเพื่อเลือกผู้เข้าร่วม

2. วิธีการจับฉลาก: เขียน ID ของสมาชิกทั้งหมดบนกระดาษ ผสมให้ทั่ว และจับจำนวนที่กำหนด

3. เครื่องมือซอฟต์แวร์: ใช้ฟังก์ชัน RAND() ของ Excel, ฟังก์ชัน sample() ของ R หรือคุณสมบัติการเลือกแบบสุ่มของ SPSS

ตัวอย่างใน Excel:

1. แสดงรายชื่อพนักงานฝ่ายขายทั้งหมด (300 คน)
2. กำหนดหมายเลขให้แต่ละคน (1-300)
3. สร้างตัวเลขสุ่ม 60 ตัวระหว่าง 1 ถึง 300 โดยใช้ =RANDBETWEEN(1,300)
4. เลือกพนักงานที่ตรงกับหมายเลขเหล่านั้น
5. ทำซ้ำสำหรับแต่ละ Stratum

ข้อกำหนดสำคัญ: การเลือกภายในแต่ละ Stratum ต้องสุ่มอย่างแท้จริง สมาชิกทุกคนของ Stratum ต้องมีความน่าจะเป็นในการถูกเลือกเท่ากัน

ขั้นตอนที่ 6: รวมกลุ่มตัวอย่างและเก็บข้อมูล

หลังจากเลือกผู้เข้าร่วมจากทุก Strata แล้ว ให้รวมพวกเขาเข้าเป็นกลุ่มตัวอย่างสุดท้ายและดำเนินการเก็บข้อมูล

องค์ประกอบกลุ่มตัวอย่างสุดท้าย (จากตัวอย่างของเรา):

• ขนาดกลุ่มตัวอย่างทั้งหมด: 200 คน
• ฝ่ายขาย: 60 (30%)
• วิศวกรรม: 80 (40%)
• การตลาด: 30 (15%)
• HR: 10 (5%)
• ปฏิบัติการ: 20 (10%)

กลุ่มตัวอย่างนี้สะท้อนการกระจายตามแผนกของประชากรอย่างสมบูรณ์แบบ ทำให้มั่นใจว่ามีการเป็นตัวแทนตามสัดส่วน

ตัวอย่างจริงของ Stratified Sampling

ตัวอย่างที่ 1: แบบสำรวจความพึงพอใจของนักศึกษามหาวิทยาลัย

คำถามวิจัย: ระดับความพึงพอใจโดยรวมของนักศึกษาในมหาวิทยาลัยคืออะไร?

ประชากร: นักศึกษาที่ลงทะเบียน 10,000 คน

ตัวแปรการแบ่งชั้น: ปีการศึกษา (ปี 1, ปี 2, ปี 3, ปี 4)

การแบ่งประชากร:

• ปี 1: 3,000 (30%)
• ปี 2: 2,500 (25%)
• ปี 3: 2,500 (25%)
• ปี 4: 2,000 (20%)

วิธีการสุ่มตัวอย่าง: Proportional Stratified Sampling โดยมีกลุ่มตัวอย่างทั้งหมด 400 คน

การจัดสรรกลุ่มตัวอย่าง:

• ปี 1: 120 คน
• ปี 2: 100 คน
• ปี 3: 100 คน
• ปี 4: 80 คน

ทำไมต้องใช้ Stratified Sampling: แต่ละปีการศึกษามีประสบการณ์และมุมมองที่แตกต่างกัน นักศึกษาปี 1 มุ่งเน้นที่การปฐมนิเทศและการปรับตัว ในขณะที่นักศึกษาปี 4 มุ่งเน้นที่การสำเร็จการศึกษาและการหางาน Stratified Sampling รับรองว่าทุกมุมมองได้รับการเป็นตัวแทนตามสัดส่วน

ปัญหาทางเลือก: หากใช้ Simple Random Sampling กับนักศึกษา 400 คน คุณอาจได้นักศึกษาปี 1 ถึง 150 คนและนักศึกษาปี 4 เพียง 50 คน ซึ่งจะไม่แสดงประสบการณ์ของนักศึกษาปี 4 อย่างเพียงพอ

ตัวอย่างที่ 2: การสำรวจความคิดเห็นทางการเมืองทั่วรัฐ

คำถามวิจัย: ผู้มีสิทธิเลือกตั้งชอบผู้สมัครคนไหนในการเลือกตั้งที่จะมาถึง?

ประชากร: ผู้มีสิทธิเลือกตั้งที่ลงทะเบียน 5,000,000 คนในรัฐ

ตัวแปรการแบ่งชั้น: ภูมิภาค (เหนือ, ใต้, ตะวันออก, ตะวันตก, กลาง)

การแบ่งประชากร:

• เหนือ: 1,500,000 (30%)
• ใต้: 1,000,000 (20%)
• ตะวันออก: 1,250,000 (25%)
• ตะวันตก: 750,000 (15%)
• กลาง: 500,000 (10%)

วิธีการสุ่มตัวอย่าง: Proportional Stratified Sampling โดยมีกลุ่มตัวอย่างทั้งหมด 2,000 คน

การจัดสรรกลุ่มตัวอย่าง:

• เหนือ: 600 คน
• ใต้: 400 คน
• ตะวันออก: 500 คน
• ตะวันตก: 300 คน
• กลาง: 200 คน

ทำไมต้องใช้ Stratified Sampling: ภูมิภาคต่างๆ มักมีความชอบทางการเมืองที่แตกต่างกันตามความแตกต่างระหว่างเมือง/ชนบท สภาพเศรษฐกิจ และประเด็นท้องถิ่น Stratified Sampling รับรองการคาดการณ์ที่แม่นยำทั่วรัฐโดยเป็นตัวแทนของอำนาจการลงคะแนนของแต่ละภูมิภาคตามสัดส่วน

ตัวอย่างที่ 3: การศึกษาการเข้าถึงบริการสุขภาพ

คำถามวิจัย: ผู้ป่วยมีความพึงพอใจในบริการโรงพยาบาลมากน้อยเพียงใด?

ประชากร: ผู้ป่วย 50,000 คนที่เข้ารับบริการในระบบโรงพยาบาลในปีที่ผ่านมา

ตัวแปรการแบ่งชั้น: ประเภทประกัน (ประกันเอกชน, Medicare, Medicaid, ไม่มีประกัน)

การแบ่งประชากร:

• ประกันเอกชน: 25,000 (50%)
• Medicare: 12,500 (25%)
• Medicaid: 10,000 (20%)
• ไม่มีประกัน: 2,500 (5%)

วิธีการสุ่มตัวอย่าง: Disproportional Stratified Sampling เพื่อให้แน่ใจว่ากลุ่มไม่มีประกันมีตัวแทนเพียงพอ

การจัดสรรกลุ่มตัวอย่าง (กลุ่มตัวอย่างทั้งหมด: 1,000):

• ประกันเอกชน: 400 (แทนที่จะเป็น 500)
• Medicare: 250
• Medicaid: 200
• ไม่มีประกัน: 150 (แทนที่จะเป็น 50)

ทำไมต้องใช้ Disproportional: กลุ่มไม่มีประกันมีขนาดเล็ก (5%) แต่มีความสำคัญอย่างยิ่งสำหรับนโยบายสุขภาพ การสุ่มตัวอย่างเพียง 50 คนที่ไม่มีประกันจะไม่ให้สถิติกำลังที่เพียงพอสำหรับการวิเคราะห์ที่มีความหมาย ด้วยการสุ่มตัวอย่างมากเกินไปใน Stratum นี้และใช้น้ำหนักทางสถิติระหว่างการวิเคราะห์ ผู้วิจัยสามารถเปรียบเทียบความพึงพอใจระหว่างประเภทประกันด้วยความแม่นยำที่เท่ากัน

ตัวอย่างที่ 4: การควบคุมคุณภาพการผลิต

คำถามวิจัย: อัตราของเสียในชุดการผลิตทั้งหมดคือเท่าไร?

ประชากร: ชุดการผลิต 100 ชุดที่ผลิตในหนึ่งเดือน

ตัวแปรการแบ่งชั้น: กะการผลิต (เช้า, บ่าย, กลางคืน)

การแบ่งประชากร:

• กะเช้า: 40 ชุด (40%)
• กะบ่าย: 35 ชุด (35%)
• กะกลางคืน: 25 ชุด (25%)

วิธีการสุ่มตัวอย่าง: Proportional Stratified Sampling โดยตรวจสอบ 20 ชุด

การจัดสรรกลุ่มตัวอย่าง:

• กะเช้า: 8 ชุด
• กะบ่าย: 7 ชุด
• กะกลางคืน: 5 ชุด

ทำไมต้องใช้ Stratified Sampling: กะต่างๆ อาจมีอัตราของเสียที่แตกต่างกันเนื่องจากความเหนื่อยล้าของคนงาน การเปลี่ยนแปลงอุณหภูมิของอุปกรณ์ หรือระดับการกำกับดูแล Stratified Sampling รับรองว่าการวิเคราะห์การควบคุมคุณภาพเป็นตัวแทนของทุกกะตามสัดส่วน

ข้อดีของ Stratified Sampling

1. รับประกันการเป็นตัวแทนของกลุ่มย่อย

Stratified Sampling รับประกันว่ากลุ่มย่อยสำคัญภายในประชากรของคุณจะได้รับการเป็นตัวแทนในกลุ่มตัวอย่าง ต่างจาก Simple Random Sampling ที่อาจทำให้กลุ่มชนกลุ่มน้อยมีตัวแทนน้อยเกินไปโดยบังเอิญ Stratified Sampling รับประกันการรวมตามสัดส่วน

ผลกระทบในทางปฏิบัติ: หาก 5% ของประชากรของคุณมาจากกลุ่มชาติพันธุ์เฉพาะ Stratified Sampling รับรองว่าประมาณ 5% ของกลุ่มตัวอย่างของคุณเป็นตัวแทนของกลุ่มนั้น ป้องกันไม่ให้เสียงของพวกเขาหายไปในข้อมูล

2. เพิ่มความแม่นยำและลด Sampling Error

เนื่องจาก Stratified Sampling คำนึงถึงความหลากหลายของประชากร มักจะสร้างการประมาณค่าที่มี Standard Error ที่เล็กกว่าเมื่อเทียบกับ Simple Random Sampling ที่มีขนาดเท่ากัน

ประโยชน์ทางสถิติ: การแบ่งชั้นลดความแปรปรวนภายใน Strata ซึ่งลด Sampling Error โดยรวม ซึ่งหมายความว่าคุณสามารถบรรลุระดับความแม่นยำเดียวกันด้วยขนาดกลุ่มตัวอย่างที่เล็กกว่า หรือความแม่นยำที่มากกว่าด้วยขนาดกลุ่มตัวอย่างเดียวกัน

3. ทำให้สามารถวิเคราะห์กลุ่มย่อยได้

ด้วยการรับประกันการเป็นตัวแทนที่เพียงพอของแต่ละ Stratum Stratified Sampling อำนวยความสะดวกในการเปรียบเทียบที่มีความหมายระหว่างกลุ่ม

คุณค่าทางวิจัย: คุณสามารถวิเคราะห์ความแตกต่างระหว่าง Strata (เช่น การเปรียบเทียบระดับความพึงพอใจระหว่างแผนก กลุ่มอายุ หรือภูมิภาค) ด้วยสถิติกำลังที่เพียงพอสำหรับแต่ละกลุ่มย่อย

4. เป็นตัวแทนของลักษณะประชากรได้ดีกว่า

กลุ่มตัวอย่างแบบแบ่งชั้นสะท้อนองค์ประกอบที่แท้จริงของประชากรในลักษณะที่ทราบได้ดีกว่า ทำให้ได้การประมาณค่าประชากรที่แม่นยำกว่า

ข้อได้เปรียบด้านความแม่นยำ: หากคุณทราบว่าประชากรของคุณเป็น 60% เมืองและ 40% ชนบท Stratified Sampling จะรักษาอัตราส่วนนี้ ทำให้ผลการค้นพบของคุณแสดงบริบททางภูมิศาสตร์ทั้งสองอย่างแม่นยำ

5. ความยืดหยุ่นในกลยุทธ์การสุ่มตัวอย่าง

ผู้วิจัยสามารถใช้การจัดสรรแบบสัดส่วน (รักษาสัดส่วนประชากร) หรือการจัดสรรแบบไม่สัดส่วน (สุ่มตัวอย่างมากเกินไปในกลุ่มเล็กแต่สำคัญ) ขึ้นอยู่กับวัตถุประสงค์การวิจัย

วิธีการที่ปรับได้: ความยืดหยุ่นนี้ช่วยให้คุณสมดุลระหว่างการเป็นตัวแทนทางสถิติกับความต้องการทางวิจัยในทางปฏิบัติ เช่น การรับประกันขนาดกลุ่มตัวอย่างขั้นต่ำสำหรับการวิเคราะห์กลุ่มย่อย

ข้อเสียของ Stratified Sampling

1. ต้องการข้อมูลประชากรที่สมบูรณ์

Stratified Sampling ต้องการความรู้โดยละเอียดเกี่ยวกับองค์ประกอบของประชากรในตัวแปรการแบ่งชั้น คุณต้องรู้วิธีจำแนกสมาชิกประชากรทุกคนก่อนการสุ่มตัวอย่าง

ความท้าทายในทางปฏิบัติ: ข้อกำหนดนี้อาจเป็นเรื่องยากหรือเป็นไปไม่ได้เมื่อ:

• รายชื่อประชากรที่สมบูรณ์ไม่มี
• ตัวแปรการแบ่งชั้นเป็นความลับหรือไม่ทราบ (เช่น ระดับรายได้, สภาวะสุขภาพ)
• ลักษณะของประชากรเปลี่ยนแปลงอย่างรวดเร็ว

ตัวอย่าง: หากคุณต้องการแบ่งชั้นตามรายได้แต่ไม่มีข้อมูลรายได้สำหรับสมาชิกประชากรทั้งหมด คุณไม่สามารถนำ Stratified Sampling ไปใช้อย่างเหมาะสม

2. ใช้เวลาและทรัพยากรมาก

การสร้าง Strata การกำหนดการจัดสรรที่เหมาะสม และการดำเนินการเลือกแบบสุ่มแยกต่างหากสำหรับแต่ละ Stratum ต้องใช้เวลาและความพยายามมากกว่า Simple Random Sampling

ผลกระทบต่อทรัพยากร:

• ความซับซ้อนในการจัดการข้อมูลเพิ่มขึ้นตามจำนวน Strata
• ต้องการขั้นตอนการสุ่มตัวอย่างแยกต่างหากสำหรับแต่ละ Stratum
• ภาระการบริหารในการติดตามกลุ่มตัวอย่างย่อยหลายกลุ่ม

3. ความเสี่ยงของการแบ่งชั้นที่ไม่เหมาะสม

การเลือกตัวแปรการแบ่งชั้นที่ผิดสามารถลดประสิทธิภาพหรือสร้างอคติ

ปัญหาที่อาจเกิดขึ้น:

• ตัวแปรที่ไม่เกี่ยวข้องสิ้นเปลืองทรัพยากรโดยไม่ปรับปรุงความแม่นยำ
• การละเลยตัวแปรการแบ่งชั้นที่สำคัญพลาดโอกาสในการลดความแปรปรวน
• ตัวแปรการแบ่งชั้นมากเกินไปสร้าง Strata ขนาดเล็กจำนวนมาก ทำให้การวิเคราะห์ซับซ้อน

ตัวอย่าง: การแบ่งชั้นตามสีตาในการสำรวจทางการเมืองเพิ่มความซับซ้อนโดยไม่ปรับปรุงความแม่นยำ เพราะสีตาไม่เกี่ยวข้องกับความชอบทางการเมือง

4. ความซับซ้อนในการวิเคราะห์ทางสถิติ

Disproportional Stratified Sampling ต้องการการถ่วงน้ำหนักทางสถิติระหว่างการวิเคราะห์เพื่อปรับการเลือกที่ไม่เป็นสัดส่วน ทำให้การวิเคราะห์ซับซ้อนขึ้น

ข้อกำหนดทางเทคนิค: ผู้วิจัยต้องใช้น้ำหนักที่เหมาะสมและใช้ขั้นตอนการวิเคราะห์ที่มีน้ำหนัก ซึ่งต้องการความเชี่ยวชาญทางสถิติและทำให้การตีความซับซ้อน

5. อาจไม่ลดอคติหาก Strata ถูกกำหนดไม่ดี

หาก Strata มีความหลากหลายภายใน (สมาชิกภายใน Stratum แตกต่างกันมาก) การแบ่งชั้นให้ประโยชน์เพียงเล็กน้อยเมื่อเทียบกับ Simple Random Sampling

ประสิทธิภาพขึ้นอยู่กับ: ตัวแปรการแบ่งชั้นจับการแบ่งประชากรที่มีความหมายได้ดีเพียงใด การเลือกการแบ่งชั้นที่ไม่ดีสิ้นเปลืองทรัพยากรโดยไม่ปรับปรุงคุณภาพกลุ่มตัวอย่าง

เมื่อไหร่ควรใช้ Stratified Sampling

Stratified Sampling เหมาะสมที่สุดในสถานการณ์วิจัยเฉพาะ ใช้วิธีนี้เมื่อ:

1. ประชากรของคุณมีความหลากหลาย

เมื่อประชากรของคุณมีกลุ่มย่อยที่แตกต่างกันซึ่งแตกต่างกันในตัวแปรที่เกี่ยวข้องกับคำถามวิจัยของคุณ Stratified Sampling รับรองว่าทุกมุมมองจะถูกจับ

ตัวชี้วัด: ประชากรแตกต่างกันอย่างมีนัยสำคัญตามข้อมูลประชากร ภูมิศาสตร์ พฤติกรรม หรือลักษณะเชิงหมวดหมู่อื่นๆ ที่สำคัญสำหรับการศึกษาของคุณ

2. คุณต้องการเปรียบเทียบกลุ่มย่อย

หากการวิจัยของคุณต้องการการวิเคราะห์และเปรียบเทียบกลุ่มต่างๆ (เช่น การเปรียบเทียบความพึงพอใจระหว่างกลุ่มอายุ ภูมิภาค หรือกลุ่มลูกค้า) Stratified Sampling รับรองการเป็นตัวแทนที่เพียงพอสำหรับการเปรียบเทียบทางสถิติ

วัตถุประสงค์การวิจัย: การศึกษาที่ออกแบบมาเพื่อระบุความแตกต่างระหว่างกลุ่มหรือตรวจสอบว่าตัวแปรทำงานแตกต่างกันอย่างไรในกลุ่มย่อยต่างๆ

3. คุณมีข้อมูลประชากรที่สมบูรณ์

Stratified Sampling ต้องการทราบตัวแปรการแบ่งชั้นสำหรับสมาชิกประชากรทุกคน ใช้วิธีนี้เฉพาะเมื่อคุณสามารถเข้าถึงข้อมูลประชากรที่สมบูรณ์และแม่นยำ

ความพร้อมของข้อมูล: ฐานข้อมูลองค์กร บันทึกของรัฐบาล หรือรายชื่อที่ครอบคลุมซึ่งรวมตัวแปรการแบ่งชั้นสำหรับสมาชิกทั้งหมด

4. กลุ่มย่อยบางกลุ่มเล็กแต่สำคัญ

เมื่อกลุ่มชนกลุ่มน้อยคิดเป็นเปอร์เซ็นต์ที่เล็กของประชากรของคุณแต่มีความสำคัญต่อการวิจัยของคุณ Disproportional Stratified Sampling ช่วยให้คุณสุ่มตัวอย่างมากเกินไปในกลุ่มเหล่านี้ในขณะที่รักษาความถูกต้องทางสถิติผ่านการถ่วงน้ำหนัก

การใช้งาน: การศึกษาประชากรที่หายาก ประสบการณ์ของชนกลุ่มน้อย หรือกลุ่มย่อยพิเศษที่จะมีตัวแทนน้อยเกินไปใน Simple Random Samples

5. คุณต้องการปรับปรุงความแม่นยำ

เมื่อความแม่นยำทางสถิติมีความสำคัญและคุณสามารถระบุตัวแปรที่อธิบายความแปรปรวนในผลลัพธ์ของคุณ Stratified Sampling ลด Sampling Error เมื่อเทียบกับ Simple Random Sampling ขนาดเท่ากัน

เป้าหมายประสิทธิภาพ: การบรรลุการประมาณค่าประชากรที่แม่นยำกว่าด้วยขนาดกลุ่มตัวอย่างที่เล็กกว่า หรือความแม่นยำที่มากกว่าด้วยทรัพยากรเดียวกัน

เมื่อไหร่ไม่ควรใช้ Stratified Sampling

หลีกเลี่ยง Stratified Sampling เมื่อ:

• คุณขาดข้อมูลเกี่ยวกับตัวแปรการแบ่งชั้นสำหรับสมาชิกประชากร
• ประชากรของคุณเป็นเนื้อเดียวกัน (สมาชิกมีความคล้ายคลึงกันในลักษณะที่เกี่ยวข้อง)
• คุณมีเวลาและทรัพยากรจำกัด และ Simple Random Sampling เพียงพอ
• ไม่มีตัวแปรการแบ่งชั้นที่ชัดเจนและเกี่ยวข้องสำหรับคำถามวิจัยของคุณ
• Strata จะไม่สมดุลมาก (เช่น Stratum หนึ่งมี 95% ของประชากร)

ข้อผิดพลาดทั่วไปใน Stratified Sampling

ข้อผิดพลาดที่ 1: Strata ทับซ้อนกัน

ปัญหา: การสร้าง Strata ที่ไม่แยกจากกันโดยเฉพาะ ทำให้สมาชิกประชากรบางคนอาจอยู่ในหลาย Strata

ตัวอย่าง: การแบ่งชั้นตาม "อายุ 18-25" และ "นักศึกษาวิทยาลัย" สร้างการทับซ้อนเพราะนักศึกษาวิทยาลัยจำนวนมากอายุ 18-25

วิธีแก้: ตรวจสอบให้แน่ใจว่าสมาชิกประชากรทุกคนอยู่ใน Stratum เดียวเท่านั้น ใช้หมวดหมู่ที่กำหนดอย่างชัดเจนและไม่ทับซ้อน

ข้อผิดพลาดที่ 2: ใช้ตัวแปรต่อเนื่องสำหรับการแบ่งชั้น

ปัญหา: พยายามแบ่งชั้นโดยใช้ตัวแปรต่อเนื่องโดยไม่สร้างหมวดหมู่ที่แยกจากกัน

ตัวอย่าง: พยายามแบ่งชั้นตาม "รายได้" โดยไม่กำหนดช่วงรายได้

วิธีแก้: แปลงตัวแปรต่อเนื่องให้เป็นช่วงเชิงหมวดหมู่ที่มีความหมาย (เช่น ช่วงรายได้: ต่ำกว่า 30,000, 30,000-60,000, 60,000-100,000, มากกว่า 100,000)

ข้อผิดพลาดที่ 3: Strata มากเกินไป

ปัญหา: การสร้าง Strata มากเกินไปที่ส่งผลให้ขนาดกลุ่มตัวอย่างต่อ Stratum เล็กมาก ลดสถิติกำลังและทำให้การวิเคราะห์ซับซ้อน

ตัวอย่าง: การแบ่งชั้นกลุ่มตัวอย่าง 100 คนด้วยตำแหน่งงาน 20 ตำแหน่งทำให้มีเพียง 5 คนต่อ Stratum โดยเฉลี่ย

วิธีแก้: จำกัดการแบ่งชั้นไว้เฉพาะตัวแปรที่สำคัญที่สุด รวม Strata ขนาดเล็กเมื่อเหมาะสม ปฏิบัติตามแนวทางของการสังเกตอย่างน้อย 30 รายต่อ Stratum สำหรับการวิเคราะห์ทางสถิติที่เพียงพอ

ข้อผิดพลาดที่ 4: ละเลยการสุ่มภายใน Stratum

ปัญหา: การเลือกผู้เข้าร่วมจาก Strata โดยใช้วิธีสะดวกหรือดุลยพินิจแทนการเลือกแบบสุ่ม

ตัวอย่าง: การเลือกผู้เข้าร่วมที่ "พร้อมใช้งานมากที่สุด" จากแต่ละแผนกแทนการสุ่มเลือก

วิธีแก้: ใช้วิธีการเลือกแบบสุ่มภายในแต่ละ Stratum เสมอ ความถูกต้องของ Stratified Random Sampling ขึ้นอยู่กับการสุ่มภายใน Strata

ข้อผิดพลาดที่ 5: ลืมถ่วงน้ำหนัก Disproportional Samples

ปัญหา: การวิเคราะห์ข้อมูลจาก Disproportional Stratified Samples โดยไม่ใช้น้ำหนักทางสถิติ ทำให้ได้การประมาณค่าประชากรที่มีอคติ

ตัวอย่าง: หากคุณสุ่มตัวอย่างมากเกินไปในกลุ่มชนกลุ่มน้อยเพื่อให้แน่ใจว่ามีตัวแทนเพียงพอ การปฏิบัติต่อการสังเกตทั้งหมดอย่างเท่าเทียมกันทำให้อิทธิพลของกลุ่มนั้นต่อสถิติโดยรวมพองตัว

วิธีแก้: เมื่อใช้การจัดสรรแบบไม่สัดส่วน ให้คำนวณและใช้น้ำหนักที่เหมาะสมระหว่างการวิเคราะห์ น้ำหนัก = (สัดส่วนประชากรของ Stratum) / (สัดส่วนกลุ่มตัวอย่างของ Stratum)

Stratified Sampling ในซอฟต์แวร์ทางสถิติ

ซอฟต์แวร์ทางสถิติส่วนใหญ่รองรับ Stratified Sampling และการวิเคราะห์แบบถ่วงน้ำหนัก:

Excel: ใช้ฟังก์ชัน RANDBETWEEN() สำหรับการเลือกแบบสุ่มภายใน Strata เป็นกระบวนการที่ต้องทำด้วยตนเองแต่เข้าถึงได้

R: ใช้ strata() จาก Sampling Package หรือ sample() กับการแบ่งกลุ่มย่อยสำหรับการเลือกแบบแบ่งชั้น

Python: ใช้ stratified_sample() จาก Pandas หรือ train_test_split() ของ scikit-learn กับการแบ่งชั้น

SPSS: ใช้ Data → Select Cases → Random sample กับ Syntax การแบ่งชั้นหรือโมดูล Complex Samples สำหรับการออกแบบและการวิเคราะห์

SAS: ใช้ PROC SURVEYSELECT กับ METHOD=SRS และคำสั่ง STRATA สำหรับ Stratified Random Sampling

Stata: ใช้คำสั่ง sample หรือ bsample กับ by-groups สำหรับการแบ่งชั้น และ svyset สำหรับการระบุการออกแบบการสำรวจ

สรุป

Stratified Sampling เป็นเทคนิคการสุ่มตัวอย่างแบบความน่าจะเป็นที่มีประสิทธิภาพซึ่งแบ่งประชากรออกเป็นกลุ่มย่อยที่เป็นเนื้อเดียวกัน จากนั้นจึงสุ่มเลือกผู้เข้าร่วมจากแต่ละ Stratum เพื่อให้แน่ใจว่ามีการเป็นตัวแทนตามสัดส่วน ด้วยการผสมผสานการแบ่งชั้นที่มีโครงสร้างกับการเลือกแบบสุ่ม วิธีการนี้รับประกันว่ากลุ่มย่อยสำคัญจะได้รับการเป็นตัวแทนอย่างเพียงพอในขณะที่รักษาความถูกต้องทางสถิติ

กุญแจสู่ความสำเร็จของ Stratified Sampling อยู่ที่การเลือกตัวแปรการแบ่งชั้นที่เหมาะสม การจัดสรรขนาดกลุ่มตัวอย่างระหว่าง Strata อย่างเหมาะสม และการดำเนินการเลือกแบบสุ่มอย่างแท้จริงภายในแต่ละ Stratum เมื่อนำไปใช้อย่างถูกต้อง Stratified Sampling เพิ่มความแม่นยำ ลด Sampling Error และทำให้สามารถวิเคราะห์กลุ่มย่อยได้อย่างมีความหมายเมื่อเทียบกับ Simple Random Sampling

ไม่ว่าคุณจะทำการวิจัยจากแบบสำรวจ การทดสอบควบคุมคุณภาพ หรือการศึกษาประชากร Stratified Sampling ให้วิธีการที่เป็นระบบในการจับความหลากหลายของประชากรในขณะที่รักษาความเข้มงวดทางสถิติ การเข้าใจว่าเมื่อไหร่ควรใช้การจัดสรรแบบสัดส่วนเทียบกับไม่สัดส่วน การหลีกเลี่ยงข้อผิดพลาดทั่วไปเช่น Strata ที่ทับซ้อน และการถ่วงน้ำหนักกลุ่มตัวอย่างที่ไม่สัดส่วนอย่างเหมาะสมระหว่างการวิเคราะห์ ช่วยให้การวิจัยของคุณสร้างผลการค้นพบที่แม่นยำและเป็นตัวแทน

เอกสารอ้างอิง

• Cochran, W. G. (1977). Sampling Techniques (3rd ed.). John Wiley & Sons.
• Lohr, S. L. (2021). Sampling: Design and Analysis (3rd ed.). Chapman and Hall/CRC.
• Thompson, S. K. (2012). Sampling (3rd ed.). Wiley.
• Scheaffer, R. L., Mendenhall III, W., Ott, R. L., & Gerow, K. G. (2011). Elementary Survey Sampling (7th ed.). Cengage Learning.