การวิเคราะห์ตัวแปรกำกับแบบ Multiple Moderation ใน R [ฉบับมืออาชีพ]

ในบทเรียนนี้ เราจะมาเรียนรู้วิธีการวิเคราะห์ Multiple Moderation ใน R กัน การศึกษาผลกระทบของตัวแปรกำกับหลายตัว (Multiple Moderators) จะช่วยให้เราเข้าใจความสัมพันธ์ที่ซับซ้อนระหว่างตัวแปรที่เราสนใจได้ลึกซึ้งยิ่งขึ้น และเปิดเผยถึง Interaction Effects ที่อาจเกิดขึ้น

การวิเคราะห์ทางสถิติมักจะเปิดเผยความสัมพันธ์ที่น่าสนใจระหว่างตัวแปรต่างๆ อย่างไรก็ตาม ความสัมพันธ์ระหว่างตัวแปรในโลกแห่งความเป็นจริงมักจะซับซ้อนกว่าที่ดูเสมอ มีปัจจัยหลายอย่างที่อาจมีอิทธิพลต่อความสัมพันธ์เหล่านี้ ทำให้การวิเคราะห์มีความซับซ้อนมากขึ้น นี่คือจุดที่แนวคิดของ Multiple Moderation เข้ามามีบทบาท ซึ่งเป็นรูปแบบหนึ่งของ Moderated Multiple Regression ที่ใช้ตรวจสอบว่าตัวแปรกำกับ (Moderating Variables) สองตัวหรือมากกว่านั้นส่งผลต่อความสัมพันธ์ระหว่าง Predictors และ Outcomes อย่างไร

หากคุณคุ้นเคยกับ Moderation อยู่แล้ว คุณก็พร้อมที่จะก้าวไปสู่ Multiple Moderation แล้ว แต่หากยังไม่คุ้นเคย คุณอาจต้องทำความเข้าใจแนวคิดของ Moderation ก่อนโดยอ่านบทความก่อนหน้าของเรา How to Run Moderation Analysis in R With a Single Moderator

นี่คือบทเรียนเชิงปฏิบัติ พร้อมชุดข้อมูลที่สามารถดาวน์โหลดได้ และคำแนะนำทีละขั้นตอนเพื่อช่วยให้คุณเชี่ยวชาญการวิเคราะห์ Multiple Moderation ใน R

Multiple Moderation Analysis คืออะไร

Moderation Analysis เป็นกลยุทธ์การวิเคราะห์ที่พยายามเปิดเผยและชี้แจงสถานการณ์ที่ความสัมพันธ์หนึ่งๆ เกิดขึ้นได้ แนวคิดพื้นฐานค่อนข้างเข้าใจง่าย: ความสัมพันธ์ระหว่างตัวแปรสองตัวอาจขึ้นอยู่กับหรือได้รับอิทธิพลจากระดับของตัวแปรอื่น ซึ่งเป็นแนวคิดที่เรียกว่า Moderation ตัวแปรกำกับ (Moderator) จะปรับเปลี่ยนทิศทางหรือความแข็งแกร่งของความสัมพันธ์ระหว่าง Predictor (หรือ Independent Variable) และ Outcome (หรือ Dependent Variable)

Simple Moderation Analysis จะศึกษาตัวแปรกำกับเพียงตัวเดียว แต่ถ้าหาก Interaction ระหว่าง Predictor และ Outcome ขึ้นอยู่กับเงื่อนไขมากกว่าหนึ่งเงื่อนไขล่ะ? นี่คือจุดที่ Multiple Moderation Analysis เข้ามามีบทบาท

ในบริบทของ Multiple Moderation เราสนใจที่จะศึกษาว่าตัวแปรกำกับสองตัวหรือมากกว่านั้นปรับเปลี่ยนผลกระทบของ Predictor Variable ต่อ Outcome Variable อย่างไร ในการแสดงให้เห็นในสมการ Multiple Regression เราจะขยาย Simple Moderation Model โดยเพิ่มพจน์สำหรับตัวแปรกำกับแต่ละตัวและ Interaction Term ในการศึกษาที่มีตัวแปรกำกับสองตัว สมการ Regression ของเราจะมีลักษณะดังนี้:

โดยที่:

• Y คือ Outcome Variable

• X คือ Predictor Variable

• M1 และ M2 คือตัวแปรกำกับทั้งสองตัว

• B0 คือ Intercept

• B1, B2, B3 คือค่า Regression Coefficients สำหรับ Main Effects ของ X, M1 และ M2 ตามลำดับ

• B4 และ B5 คือค่า Coefficients สำหรับ Two-Way Interaction Terms X*M1 และ X*M2 ซึ่งแสดงถึง Moderation Effects ของตัวแปรกำกับแต่ละตัว

• B6 คือค่า Coefficient สำหรับ Two-Way Interaction ระหว่างตัวแปรกำกับทั้งสอง M1*M2

• B7 คือค่า Coefficient สำหรับ Three-Way Interaction Term XM1M2 ซึ่งแสดงถึง Combined Moderation Effect ของตัวแปรกำกับทั้งสองพร้อมกัน

• e คือ Error Term ซึ่งแสดงถึง Residual Variance ที่ไม่สามารถอธิบายได้โดย Predictors และ Moderators

ตัวอย่างของ Multiple Moderation Analysis

มาพิจารณาตัวอย่างที่เกี่ยวข้องกับวิทยาศาสตร์การออกกำลังกาย สมมติว่าคุณกำลังศึกษาผลของโปรแกรมการฝึก (Predictor Variable, X) ต่อผลการแข่งขันของนักกีฬา (Outcome Variable, Y) คุณเสนอว่าอายุของนักกีฬา (Moderator แรก, M1) และจำนวนปีของการฝึกก่อนหน้านี้ (Moderator ที่สอง, M2) อาจมีอิทธิพลต่อประสิทธิผลของโปรแกรมการฝึก

ในกรณีนี้ Multiple Moderation Analysis ช่วยให้เราตรวจสอบว่าผลของโปรแกรมการฝึกต่อผลการแข่งขันของนักกีฬาแตกต่างกันหรือไม่สำหรับกลุ่มอายุต่างๆ และระดับประสบการณ์การฝึกก่อนหน้านี้ต่างๆ กล่าวอีกนัยหนึ่ง การวิเคราะห์ช่วยให้เรากำหนดว่าอิทธิพลของโปรแกรมการฝึกต่อผลการแข่งขันถูกกำกับ (Moderated) โดยทั้งอายุและจำนวนปีของการฝึกก่อนหน้านี้หรือไม่

โดยการทำความเข้าใจผลของตัวแปรกำกับหลายตัวเหล่านี้ เราได้รับมุมมองที่ละเอียดยิ่งขึ้นว่าโปรแกรมการฝึกของเรามีผลกระทบต่อประสิทธิภาพอย่างไรและภายใต้เงื่อนไขใด การวิจัยประเภทนี้สามารถนำไปสู่โปรแกรมการฝึกที่เฉพาะเจาะจงมากขึ้นซึ่งคำนึงถึงอายุและประสบการณ์การฝึกก่อนหน้านี้ของนักกีฬา

ดังนั้น ทำไม Multiple Moderation Analysis จึงมีความสำคัญ? จุดแข็งของแนวทางนี้อยู่ที่ความสามารถในการเปิดเผยความสัมพันธ์ที่ซับซ้อนและหลากหลาย แทนที่จะสำรวจความสัมพันธ์ตรงไปตรงมาระหว่างตัวแปร Multiple Moderation Analysis ให้ความเข้าใจว่าภายใต้สถานการณ์ใดหรือสำหรับใครความสัมพันธ์เหล่านี้มีความเกี่ยวข้อง

วิธีนี้สามารถเน้นย้ำว่าอิทธิพลของ Independent Variable ต่อ Dependent Variable อาจเปลี่ยนแปลงไปตามระดับของตัวแปรกำกับสองตัวหรือมากกว่านั้นอย่างไร ทำให้เกิดความเข้าใจที่ลึกซึ้งและหลากหลายมากขึ้นเกี่ยวกับความเป็นไปแบบต่างๆ

โดยการตอบคำถามที่สอดคล้องกับความซับซ้อนของสถานการณ์ในชีวิตจริงมากขึ้น Multiple Moderation Analysis เป็นเครื่องมือที่แข็งแกร่งสำหรับการวิจัยในสาขาต่างๆ เพิ่มพูนความเข้าใจของเราเกี่ยวกับโลกรอบตัวเรา

ข้อสมมติฐาน (Assumptions) ของ Multiple Moderation Analysis

• Linearity และ Additivity: ความสัมพันธ์ระหว่าง Predictors (รวมถึง Interaction Terms) และ Outcome Variable ควรเป็นเชิงเส้น และผลกระทบของ Predictors ต่างๆ ควรเป็น Additive ซึ่งหมายความว่าผลกระทบของ Predictor หนึ่งต่อ Outcome Variable ไม่ควรเปลี่ยนแปลงตามค่าของ Predictor อื่น ยกเว้นตามที่กำหนดโดย Interaction Term คุณสามารถเรียนรู้เพิ่มเติมเกี่ยวกับความสำคัญของ Linearity ได้ที่นี่

• Independence of Errors: Residuals (Errors) ของโมเดล นั่นคือ ความแตกต่างระหว่างค่าที่สังเกตได้และค่าที่คาดการณ์ของ Outcome Variable ควรเป็นอิสระต่อกัน ซึ่งหมายความว่าค่าของ Residual สำหรับการสังเกตหนึ่งไม่ควรคาดการณ์ค่าของ Residual สำหรับการสังเกตอื่น คุณสามารถเรียนรู้เพิ่มเติมเกี่ยวกับIndependence of Errors ได้ที่นี่

• Homoscedasticity: ความแปรปรวน (Variance) ของ Residuals ควรคงที่ในทุกระดับของ Predictors ซึ่งหมายความว่าการกระจายของ Residuals ควรมีค่าใกล้เคียงกันสำหรับทุกค่าของ Predictors คุณสามารถเรียนรู้เพิ่มเติมว่าทำไมHomoscedasticity จึงมีความสำคัญในสถิติได้ที่นี่

• Normality of Errors: Residuals ของโมเดลควรมีการแจกแจงแบบปกติโดยประมาณ ซึ่งหมายความว่าหากเราวาดกราฟความถี่ของ Residuals กราฟควรมีรูปร่างคล้ายกับเส้นโค้งรูประฆัง เรียนรู้เพิ่มเติมเกี่ยวกับNormality of Errors ได้ที่นี่

• Absence of Multicollinearity: Predictors ในโมเดลไม่ควรมีความสัมพันธ์อย่างสมบูรณ์ (Perfectly Correlated) กัน สมมติว่ามี Perfect Multicollinearity (หรือแม้แต่ High Multicollinearity) ในกรณีนั้น ก็หมายความว่า Predictors สองตัวหรือมากกว่านั้นกำลังให้ข้อมูลเดียวกันแก่เราเกี่ยวกับความแปรปรวนใน Outcome Variable ทำให้ยากต่อการระบุผลกระทบอิสระของ Predictor แต่ละตัว คุณสามารถเรียนรู้เพิ่มเติมเกี่ยวกับMulticollinearity ได้ที่นี่

• No Influential Outliers: ไม่ควรมี Data Point เดียวที่มีอิทธิพลอย่างมากเกินไปต่อการประมาณค่าของโมเดล แม้ว่า Outliers จะไม่ใช่เรื่องแปลก แต่ Outliers ที่มีอิทธิพลมากเป็นพิเศษสามารถบิดเบือนผลลัพธ์ของโมเดลและลดความแม่นยำของการคาดการณ์ของคุณ

ในบริบทของ Multiple Moderation Analysis ข้อสมมติฐานเหล่านี้ช่วยให้มั่นใจว่าผลลัพธ์ของเราน่าเชื่อถือและเราหลีกเลี่ยงการตีความที่ผิดพลาด แม้ว่าการละเมิดข้อสมมติฐานบางข้อเล็กน้อยอาจไม่ส่งผลกระทบต่อโมเดลอย่างมาก แต่การละเมิดที่รุนแรงหรือหลายข้ออาจชี้ให้เห็นว่า Multiple Moderation Analysis อาจไม่ใช่วิธีที่เหมาะสมที่สุดสำหรับข้อมูลของเรา

การกำหนดโมเดล Multiple Moderation Analysis

มาจินตนาการว่าเราสนใจที่จะศึกษาผลกระทบของการออกกำลังกาย (Physical Exercise) ต่อสุขภาพจิต (Mental Health) โดยเฉพาะอย่างยิ่ง เราสนใจที่จะทำความเข้าใจบทบาทของตัวแปรกำกับที่เป็นไปได้สองตัว คือ "คุณภาพของการนอนหลับ" (Quality of Sleep) และ "อาหารที่สมดุล" (Balanced Diet) ในความสัมพันธ์นี้

นี่คือลักษณะที่คำถามการวิจัยของเราอาจมี:"คุณภาพของการนอนหลับและการมีอาหารที่สมดุลกำกับความสัมพันธ์ระหว่างการออกกำลังกายและสุขภาพจิตอย่างไร?"

จากคำถามการวิจัยนี้ เราอาจกำหนดสมมติฐานดังนี้:

• การออกกำลังกายมีผลกระทบเชิงบวกต่อสุขภาพจิต

• ผลกระทบเชิงบวกของการออกกำลังกายต่อสุขภาพจิตจะแข็งแกร่งขึ้นสำหรับบุคคลที่มีคุณภาพการนอนหลับที่ดีกว่า

• ผลกระทบเชิงบวกของการออกกำลังกายต่อสุขภาพจิตจะแข็งแกร่งขึ้นสำหรับบุคคลที่รับประทานอาหารที่สมดุล

ตอนนี้ มาวาดแผนภาพที่แสดงความสัมพันธ์และ Interactions ที่เราเสนอในคำถามการวิจัยและสมมติฐานที่เกี่ยวข้องกัน:

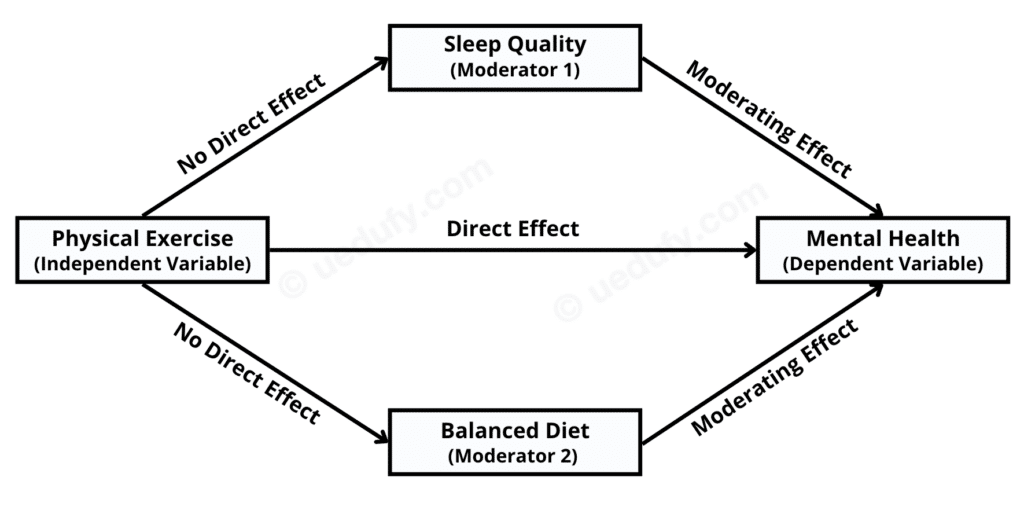ภาพที่ 1: โมเดล Multiple Moderation Analysis ที่มีตัวแปรกำกับสองตัว

โดยที่:

• Physical Exercise (Independent Variable): นี่คือ Independent Variable ของเรา เป็นปัจจัยหลักที่เรากำลังศึกษาสำหรับผลกระทบที่เป็นไปได้ต่อสุขภาพจิต สามารถวัดได้ในหลายวิธี เช่น จำนวนชั่วโมงของการออกกำลังกายต่อสัปดาห์ ประเภทของการออกกำลังกายที่ทำ เป็นต้น

• Mental Health (Dependent Variable): นี่คือ Dependent Variable ของเรา ความสนใจหลักของเราอยู่ที่การทำความเข้าใจว่าการออกกำลังกายอาจมีอิทธิพลต่อตัวแปรนี้อย่างไร สุขภาพจิตสามารถวัดได้ผ่านเกณฑ์หลายอย่าง เช่น แบบสำรวจที่รายงานด้วยตนเอง การประเมินทางคลินิก เป็นต้น

• Sleep Quality (Moderator 1) และ Balanced Diet (Moderator 2) คือตัวแปรกำกับของเรา เราตั้งสมมติฐานว่าปัจจัยเหล่านี้สามารถปรับเปลี่ยนความสัมพันธ์ระหว่างการออกกำลังกายและสุขภาพจิต ตามลำดับ ผลของการออกกำลังกายต่อสุขภาพจิตอาจเปลี่ยนแปลงไปตามระดับของตัวแปรกำกับเหล่านี้

ผลกระทบ ดังที่แสดงโดยลูกศรในแผนภาพข้างต้น มีดังนี้:

• Direct Effect: ลูกศรนี้แสดงถึงผลกระทบโดยตรงที่การออกกำลังกาย (Independent Variable) อาจมีต่อสุขภาพจิต (Dependent Variable)

• Moderating Effects: ลูกศรเหล่านี้แสดงถึงอิทธิพลที่เป็นไปได้ที่ตัวแปรกำกับของเรา (Sleep Quality และ Balanced Diet) อาจมีต่อความสัมพันธ์ระหว่างการออกกำลังกายและสุขภาพจิต โดยเฉพาะอย่างยิ่ง ผลกระทบเหล่านี้แสดงว่าความสัมพันธ์ระหว่างการออกกำลังกายและสุขภาพจิตอาจเปลี่ยนแปลงไปที่ระดับต่างๆ ของตัวแปรกำกับอย่างไร

• No Direct Effect: ลูกศรเหล่านี้ระบุว่าเราไม่ตั้งสมมติฐานถึงผลกระทบโดยตรงจากการออกกำลังกาย (Independent Variable) ไปยังตัวแปรกำกับใดๆ (Sleep Quality และ Balanced Diet)

ในขณะที่เราดำเนินการต่อไป แผนภาพจะช่วยอย่างมากในการรักษาความเข้าใจแนวคิดที่ชัดเจนเกี่ยวกับความสัมพันธ์ที่เรากำลังทดสอบและตีความในการวิเคราะห์ของเรา

วิธีการวิเคราะห์ Multiple Moderation ใน R

หลังจากที่เราได้วางรากฐานทางทฤษฎีที่แข็งแกร่งเกี่ยวกับ Multiple Moderation Analysis แล้ว ก็ถึงเวลาที่จะนำทฤษฎีไปสู่การปฏิบัติโดยการทำการวิเคราะห์ Moderation ใน R

หากคุณยังไม่ได้ติดตั้ง R หรือ R Studio นี่คือคู่มือที่เป็นประโยชน์สำหรับเริ่มต้นการติดตั้ง R และ R Studio บน Windows, macOS, Linux และ Unix ตอนนี้ มาพับแขนเสื้อและเจาะลึกเข้าไปในกระบวนการทำการวิเคราะห์ Moderation ที่มีตัวแปรกำกับหลายตัวใน R กัน

ชุดข้อมูลประกอบด้วยข้อมูลจำลองสำหรับผู้ตอบแบบสอบถาม 30 คนและตัวแปร 4 ตัว และจะใช้เพื่อวัตถุประสงค์ทางการศึกษาเท่านั้น หรือคุณสามารถใช้ชุดข้อมูลของคุณเองและทำตามคำแนะนำต่อไปได้

ขั้นตอนที่ 1: โหลดข้อมูลและ Packages ที่จำเป็นใน R

ก่อนที่จะดำเนินการวิเคราะห์ เราต้องโหลดข้อมูลของเราเข้าสู่ R เนื่องจากชุดข้อมูลของเราอยู่ในไฟล์ Excel เราสามารถใช้ Package readxl เพื่อ Import ข้อมูลได้อย่างสะดวก

สำหรับการวิเคราะห์ Moderation ของเรา เราจะใช้ Packages สำคัญสองตัว ตัวแรกคือ jtools ซึ่งให้ Functions ที่ใช้งานง่ายที่ทำให้ Regression Models เข้าใจและตีความได้ง่ายขึ้น Package ที่สองคือ interactions ซึ่งออกแบบมาโดยเฉพาะสำหรับการสำรวจและแสดงผล Interactions ภายใน Regression Models ทำให้เป็นเครื่องมือที่เหมาะสำหรับ Moderation Analysis

การรวม Packages เหล่านี้จะทำให้เราสามารถทำการวิเคราะห์ Moderation ที่ครอบคลุมและเข้าใจได้ง่ายด้วยภาพ

# Install the necessary packages
install.packages("readxl")
install.packages("jtools")
install.packages("interactions")

# Load the packages
library(readxl)
library(jtools)
library(interactions)

# Load the data into data frame
data <- read_excel("Path_to_your_file/data.xlsx")

ในโค้ดนี้ ให้แทนที่ "**Path_to_your_file/data.xlsx**" ด้วยเส้นทางจริงไปยังไฟล์ Excel ของคุณ

สำคัญ: หากคุณเลือกที่จะ Import ชุดข้อมูลของคุณผ่าน RStudio GUI คุณยังคงต้องเพิ่ม data <- read_excel("Path_to_your_file/data.xlsx") ลงในสคริปต์ของคุณ มิฉะนั้นชุดข้อมูลของคุณจะไม่ถูกโหลดเข้าสู่ Data Frame ใน R อย่าลืมใส่เส้นทางไปยังชุดข้อมูลของคุณไว้ระหว่างเครื่องหมายคำพูด นี่คือแหล่งข้อมูลที่เป็นประโยชน์สำหรับการ Import ชุดข้อมูลในรูปแบบต่างๆ เข้าสู่ R - เผื่อว่าคุณพบปัญหา:

• How To Import An Excel File into R

• How To Import A CSV File into R

ขั้นตอนที่ 2: สำรวจข้อมูล

ก่อนที่จะเจาะลึกเข้าไปในการวิเคราะห์ การสำรวจและทำความเข้าใจข้อมูลของคุณเป็นความคิดที่ดีเสมอ เราจะใช้ Function str เพื่อแสดงโครงสร้างของชุดข้อมูลของเรา

# Explore the structure of the data
str(data)

Function str จะแสดงชื่อของตัวแปรของคุณและรายการแรกๆ ในแต่ละตัวแปร

ภาพที่ 2: โครงสร้างชุดข้อมูลใน R แสดง 30 ผู้ตอบแบบสอบถามและ 4 ตัวแปร

ขั้นตอนที่ 3: การสร้าง Regression Model

ขั้นตอนต่อไปของเราคือการสร้าง Regression Model กับข้อมูลของเรา โมเดลนี้รวมถึง Interaction Terms สำหรับตัวแปรกำกับของเรา เราจะใช้ Function lm ใน R ซึ่งสร้าง Ordinary Least Squares (OLS) Regression Model กับข้อมูล

# Fit the model
model <- lm(mental_health ~ exercise * sleep_quality * balanced_diet, data = data)

สำคัญ: ในสคริปต์ข้างต้น โปรดรักษาชื่อตัวแปรให้ตรงตามที่อยู่ในชุดข้อมูลของคุณ มิฉะนั้น R จะไม่สามารถหา Object ที่เกี่ยวข้องได้

เช่น หากเรามีชื่อตัวแปร mental_health ในชุดข้อมูลของเรา ให้ใช้มันตามนั้นและไม่ใช่ Mental_Health หรือ MentalHealth

ในโมเดล เครื่องหมายดอกจัน (**) แสดงถึง Interaction Terms Interaction Term คือตัวแปรที่สร้างขึ้นโดยการคูณสองตัวแปรอื่น ในกรณีของเรา เราสนใจใน Interaction ของ exercise กับทั้ง sleep_quality และ balanced_diet โมเดลข้างต้นพิจารณา Interactions ที่เป็นไปได้ทั้งหมดระหว่าง Independent Variable และ Moderators ของเรา

โปรดทราบว่าเราไม่คาดหวังให้ R ให้ Output ใดๆ กับโค้ดข้างต้น ที่นี่เราเพียงแค่สร้างโมเดล และในขั้นตอนต่อไปเราจะเห็นผลลัพธ์

ต่อไป เราจะประเมินความสำคัญของโมเดล ตรวจสอบข้อสมมติฐานของ Regression และตีความการค้นพบของเรา

ขั้นตอนที่ 4: ตรวจสอบผลลัพธ์ Multiple Moderation Analysis

เมื่อสร้างโมเดลแล้ว ขั้นตอนต่อไปคือการตรวจสอบผลลัพธ์ของการวิเคราะห์ สำหรับสิ่งนี้ เราจะใช้ Function summary() เพื่อแสดงสรุปผลลัพธ์ของโมเดล ต่อไปนี้คือวิธีการ:

# Display a summary of the model's results
summary(model)

การรันโค้ดนี้จะให้ Output ที่รวมถึง Coefficients สำหรับ Main Effects ของแต่ละ Independent Variable (exercise, sleep_quality, balanced_diet) รวมถึง Interaction Terms (exercise:sleep_quality, exercise:balanced_diet, sleep_quality:balanced_diet และ exercise:sleep_quality:balanced_diet)

นี่คือลักษณะของ Summary Output:

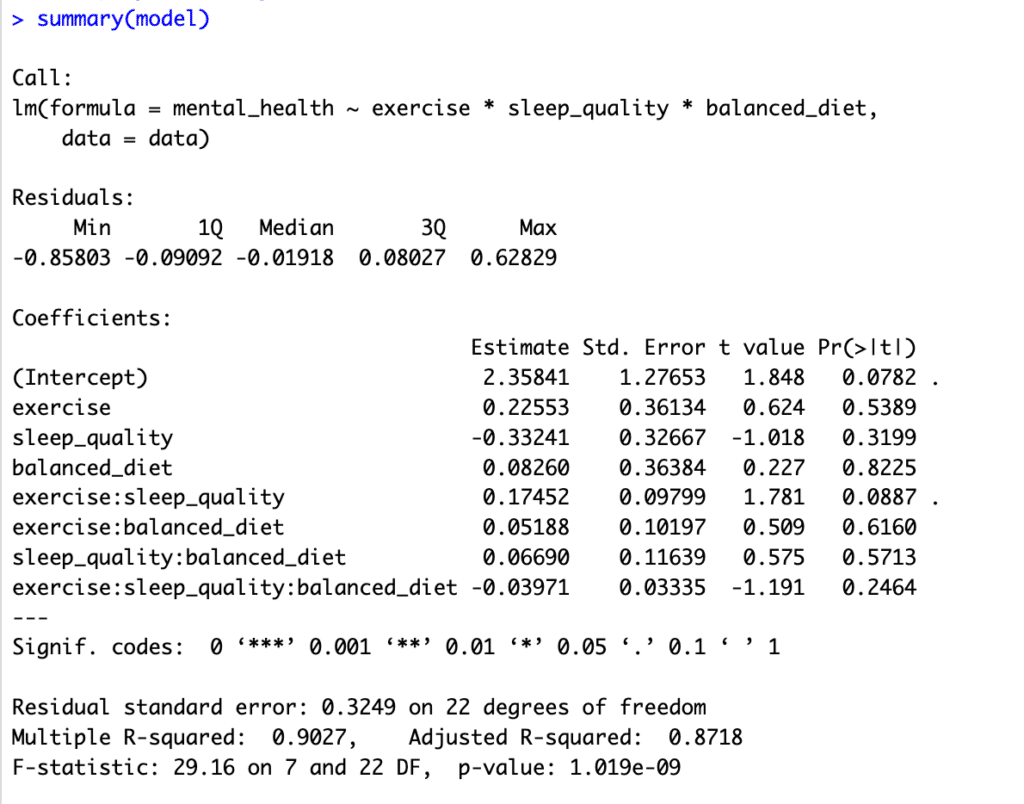ภาพที่ 3: ผลลัพธ์ Multiple Moderation Analysis แสดง Interaction Effects

Coefficients สำหรับ Interaction Terms เป็นสิ่งที่สนใจหลักใน Moderation Analysis เพราะพวกมันบอกเราว่าความสัมพันธ์ระหว่าง Independent Variable (exercise) และ Dependent Variable (mental_health) เปลี่ยนแปลงไปอย่างไรเป็น Function ของตัวแปรกำกับ (sleep_quality, balanced_diet)

หาก Coefficient ของ Interaction Term แตกต่างจากศูนย์อย่างมีนัยสำคัญ (p < 0.05) เราสามารถสรุปได้ว่าผลของ Independent Variable ต่อ Dependent Variable ถูกกำกับโดยตัวแปรที่เกี่ยวข้อง

ขั้นตอนที่ 5: การตีความผลลัพธ์ Multiple Moderation Analysis

การตีความผลลัพธ์จาก Multiple Moderation Analysis อาจมีความท้าทาย โดยเฉพาะอย่างยิ่งเมื่อมี Interaction Terms หลายตัว อย่างไรก็ตาม หลักการพื้นฐานยังคงเหมือนเดิม: หาก Interaction Term มีนัยสำคัญ มันบอกว่าความสัมพันธ์ระหว่าง Independent Variable และ Dependent Variable ถูกกำกับโดยตัวแปรที่เกี่ยวข้อง

นี่คือวิธีที่เราตีความ Model Summary Output ข้างต้น:

• Interaction Term exercise:sleep_quality มีค่า p-value เท่ากับ 0.0887 ซึ่งอยู่เหนือ Threshold มาตรฐาน 0.05 สำหรับความสำคัญทางสถิติเล็กน้อย แต่อาจถูกพิจารณาว่า "มีนัยสำคัญเล็กน้อย" หรือ "แนวโน้ม" ไปสู่ความสำคัญ นี่บอกว่าอาจมี Moderation Effect ของคุณภาพการนอนหลับต่อความสัมพันธ์ระหว่างการออกกำลังกายและสุขภาพจิต แต่หลักฐานไม่แข็งแกร่งพอที่จะแน่ใจที่ระดับ 0.05 มาตรฐาน

• Interaction Term exercise:balanced_diet มีค่า p-value เท่ากับ 0.6160 บอกว่าหลักฐานไม่แข็งแกร่งพอที่จะสรุปว่าอาหารที่สมดุลกำกับความสัมพันธ์ระหว่างการออกกำลังกายและสุขภาพจิต

• Three-Way Interaction Term exercise:sleep_quality:balanced_diet มีค่า p-value เท่ากับ 0.2464 บอกว่าหลักฐานไม่แข็งแกร่งพอที่จะสรุปว่าผลของการออกกำลังกายต่อสุขภาพจิตถูกกำกับโดยทั้งคุณภาพการนอนหลับและอาหารที่สมดุลในเวลาเดียวกัน

• การประมาณค่า Coefficients แสดงถึงการเปลี่ยนแปลงใน Dependent Variable (สุขภาพจิต) สำหรับการเพิ่มขึ้นหนึ่งหน่วยใน Independent Variable ที่เกี่ยวข้อง โดยสมมติว่าตัวแปรอื่นๆ ทั้งหมดคงที่

• Residual Standard Error เป็นการวัดคุณภาพของ Linear Regression Model - ตัวเลขที่ต่ำกว่าโดยทั่วไปบอกถึงการพอดีกับข้อมูลที่ดีกว่า

• ค่า R-squared เป็นการวัดทางสถิติที่แสดงถึงสัดส่วนของความแปรปรวนสำหรับ Dependent Variable ที่อธิบายโดย Independent Variable หรือหลายตัวใน Regression Model ในกรณีนี้ ประมาณ 90% ของความแปรปรวนในสุขภาพจิตถูกอธิบายโดยการออกกำลังกาย คุณภาพการนอนหลับ อาหารที่สมดุล และ Interactions โดยทั่วไปนี้ถือว่าเป็น R-squared ที่สูงมากและบอกถึงการพอดีที่ดีสำหรับโมเดล

ขั้นตอนที่ 6: แสดงผล Interaction Effect ด้วยกราฟ

มักจะเป็นประโยชน์ที่จะวาดกราฟ Interactions เพื่อให้ความสัมพันธ์เหล่านี้เข้าใจได้ง่ายขึ้น คุณสามารถใช้ Function interact_plot() จาก Package jtools นี่คือวิธีการวาดกราฟ Interaction ระหว่าง exercise, sleep_quality และ balanced_diet:

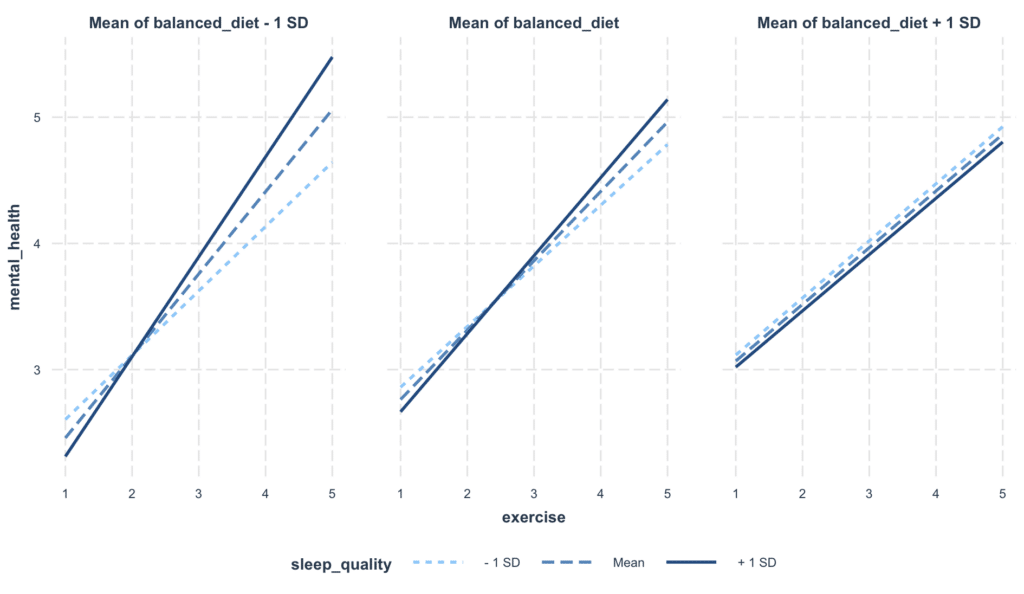ภาพที่ 4: การแสดงผล Interaction Effects ใน Multiple Moderation Analysis

โดยที่:

• แกน x แสดงระดับของการออกกำลังกาย ตั้งแต่ค่าต่ำกว่าไปยังค่าสูงกว่า

• แกน y แสดงคะแนนสุขภาพจิต โดยค่าที่สูงกว่าบอกถึงสุขภาพจิตที่ดีกว่า

• มีสองเส้น หนึ่งสำหรับอาหารที่สมดุลสูง (เส้นทึบ) และหนึ่งสำหรับอาหารที่สมดุลต่ำ (เส้นประ) เส้นเหล่านี้บอกคะแนนสุขภาพจิตที่คาดการณ์ตามระดับของการออกกำลังกายและอาหารที่สมดุล

• การแรเงารอบแต่ละเส้นแสดงถึง Confidence Interval รอบการคาดการณ์ เมื่อพื้นที่ที่แรเงาเหล่านี้ไม่ทับซ้อนกัน มันโดยทั่วไปบอกถึงความแตกต่างที่มีนัยสำคัญทางสถิติ

• กราฟถูกแบ่งตามระดับของคุณภาพการนอนหลับ บอกว่าความสัมพันธ์แยกต่างหากถูกวาดสำหรับระดับต่ำ ปานกลาง และสูงของคุณภาพการนอนหลับ

จากกราฟนี้ เราสามารถสรุปเบื้องต้นได้ว่า:

• สำหรับคนที่มีคุณภาพการนอนหลับต่ำกว่า (แผงซ้ายสุด) ดูเหมือนจะมีความแตกต่างเล็กน้อยในคะแนนสุขภาพจิตตามระดับของการออกกำลังกายหรือว่าพวกเขามีอาหารที่สมดุลสูงหรือต่ำ นี่บอกว่าคุณภาพการนอนหลับอาจเป็นตัวกำหนดสำคัญของสุขภาพจิตสำหรับกลุ่มนี้ แซงหน้าผลของการออกกำลังกายและอาหาร

• สำหรับคนที่มีคุณภาพการนอนหลับปานกลาง (แผงกลาง) เราเริ่มเห็นความแตกต่างบางอย่าง โดยเฉพาะอย่างยิ่ง บุคคลที่มีอาหารที่สมดุลสูง (เส้นทึบ) ดูเหมือนจะได้ประโยชน์จากการออกกำลังกายในแง่ของคะแนนสุขภาพจิตมากกว่าผู้ที่มีอาหารที่สมดุลต่ำ (เส้นประ)

• สำหรับคนที่มีคุณภาพการนอนหลับสูง (แผงขวาสุด) การออกกำลังกายดูเหมือนจะปรับปรุงสุขภาพจิตอย่างมีนัยสำคัญสำหรับผู้ที่มีอาหารที่สมดุลสูง (เส้นทึบ) อย่างไรก็ตาม สำหรับผู้ที่มีอาหารที่สมดุลต่ำ (เส้นประ) การออกกำลังกายดูเหมือนจะไม่นำไปสู่การปรับปรุงสำคัญในสุขภาพจิต

ขั้นตอนที่ 7: ประเมินข้อสมมติฐานและการวินิจฉัยของโมเดล

เนื่องจาก Multiple Moderation Analysis อิงจาก Regression การตรวจสอบข้อสมมติฐานของโมเดลจึงมีความสำคัญเพื่อให้แน่ใจว่าผลลัพธ์ที่เราตีความนั้นถูกต้อง การละเมิดข้อสมมติฐานเหล่านี้อาจนำไปสู่ผลลัพธ์ที่ไม่ถูกต้อง โดยเฉพาะอย่างยิ่งสำหรับโมเดล Multiple Moderation ของเรา ข้อสมมติฐานหลักรวมถึง:

1. Linearity & Additivity

ความสัมพันธ์ระหว่าง Predictors (รวมถึง Interaction Terms) และ Outcome Variable ควรเป็นเชิงเส้น และผลกระทบของ Predictors ต่างๆ ควรเป็น Additive ซึ่งหมายความว่าผลกระทบของ Predictor หนึ่งต่อ Outcome Variable ไม่ควรเปลี่ยนแปลงตามค่าของ Predictor อื่น ยกเว้นตามที่กำหนดโดย Interaction Term

นี่คือโค้ดสำหรับตรวจสอบ Linearity และ Additivity ใน R:

# Check for linearity and additivity
plot(model$fitted.values, model$residuals,
 xlab = "Predicted values", ylab = "Residuals")
abline(h = 0, col = "red")

เราสามารถตรวจสอบสิ่งนี้โดยการวาดกราฟ Residuals (ความแตกต่างระหว่างค่าที่สังเกตได้และค่าที่คาดการณ์) กับค่าที่คาดการณ์ รูปแบบที่ไม่สุ่มจะบอกถึงการละเมิดข้อสมมติฐาน Linearity

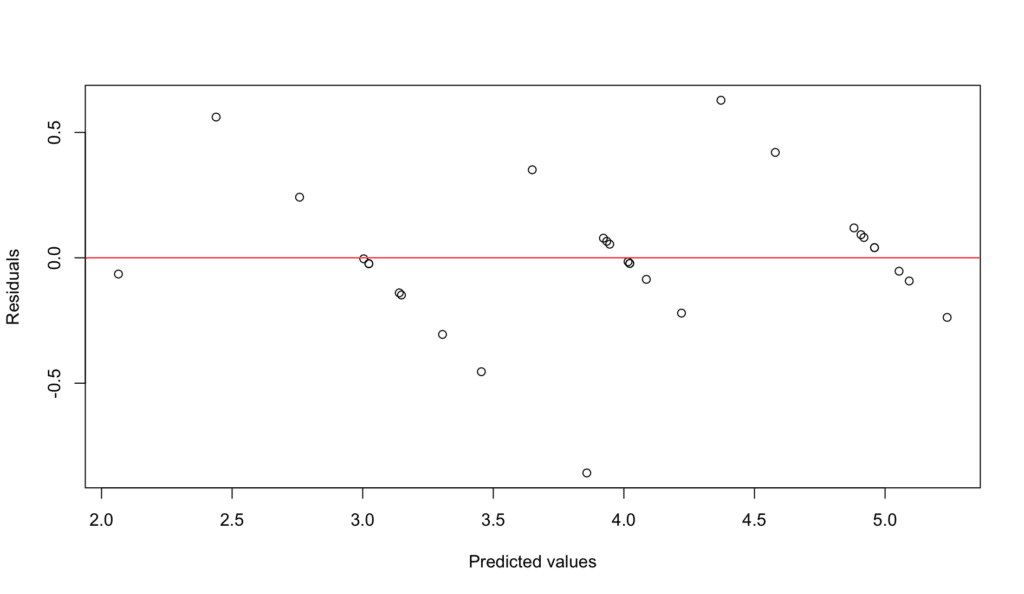ภาพที่ 5: การตรวจสอบข้อสมมติฐาน Linearity - กราฟ Residuals vs Fitted Values

2. Independence of Residuals

Residuals (Errors) ของโมเดล นั่นคือ ความแตกต่างระหว่างค่าที่สังเกตได้และค่าที่คาดการณ์ของ Outcome Variable ควรเป็นอิสระต่อกัน ซึ่งหมายความว่าค่าของ Residual สำหรับการสังเกตหนึ่งไม่ควรคาดการณ์ค่าของ Residual สำหรับการสังเกตอื่น

เราสามารถตรวจสอบข้อสมมติฐานนี้โดยใช้ Durbin-Watson Test หรือสร้างAutocorrelation Function (ACF) Plot สำหรับข้อมูล Time-Series หรือ Clustered Data เนื่องจากเรามีข้อมูล Cross-Sectional ข้อสมมติฐานนี้จึงมีความเกี่ยวข้องน้อยกว่า

อย่างไรก็ตาม หากข้อมูลของคุณเป็น Time-Series หรือข้อมูลที่ลำดับของการสังเกตมีความสำคัญ สคริปต์ด้านล่างจะสร้าง ACF Plot ใน R โปรดทราบว่าต้องติดตั้งและโหลด Package "forecast" ก่อน:

# Load the package
install.packages("forecast")
library(forecast)

# Create the ACF plot
Acf(model$residuals, main="ACF of Model Residuals")

ในกราฟนี้ แกน x แสดงถึง Lag และแกน y แสดงถึง Autocorrelation ที่แต่ละ Lag เส้นแนวตั้งแต่ละเส้น (หรือ Spike) บนกราฟสอดคล้องกับ Autocorrelation ที่ Lag นั้น หากเส้นข้าม Blue Dashed Line (ขอบเขตความสำคัญ) มันบอกว่า Residuals ไม่เป็นอิสระที่ Lag นั้น

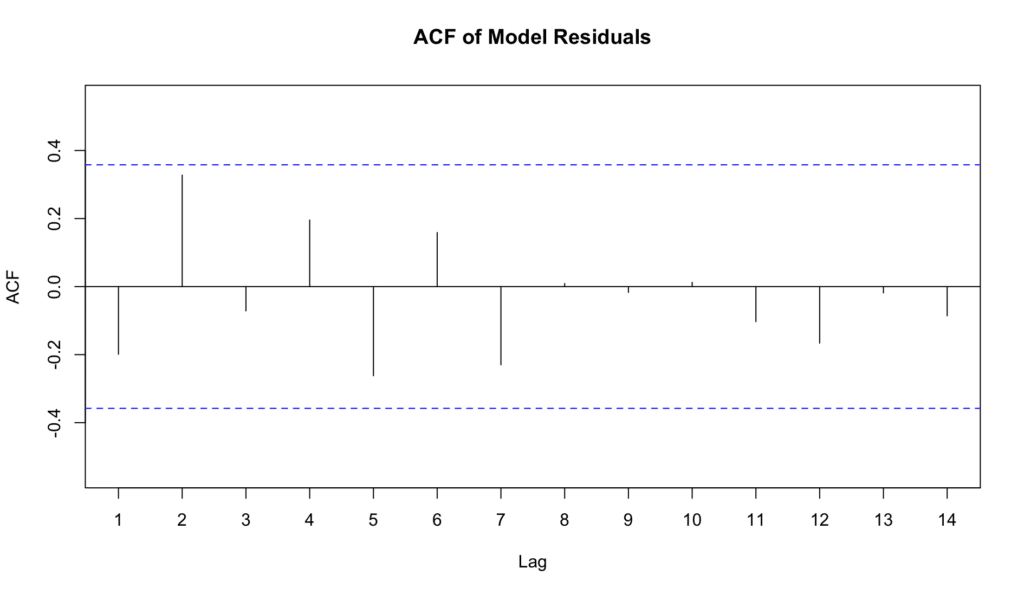ภาพที่ 6: ACF Plot สำหรับการทดสอบ Independence of Residuals

3. Homoscedasticity

ความแปรปรวนของ Residuals ควรคงที่ในทุกระดับของ Predictors ซึ่งหมายความว่าการกระจายของ Residuals ควรมีค่าใกล้เคียงกันสำหรับทุกค่าของ Predictors

นี่คือโค้ดสำหรับทดสอบ Homoscedasticity ใน R:

# Check for homoscedasticity
plot(model$fitted.values, abs(model$residuals),
 xlab = "Predicted values", ylab = "Absolute Residuals")

เราสามารถตรวจสอบสิ่งนี้โดยการดูกราฟ Residual vs Fitted เดียวกันที่เราใช้สำหรับ Linearity หากจุดกระจายสุ่มรอบเส้นแนวนอนโดยไม่มีรูปแบบที่มองเห็นได้ ข้อสมมติฐานนี้ก็เป็นจริง

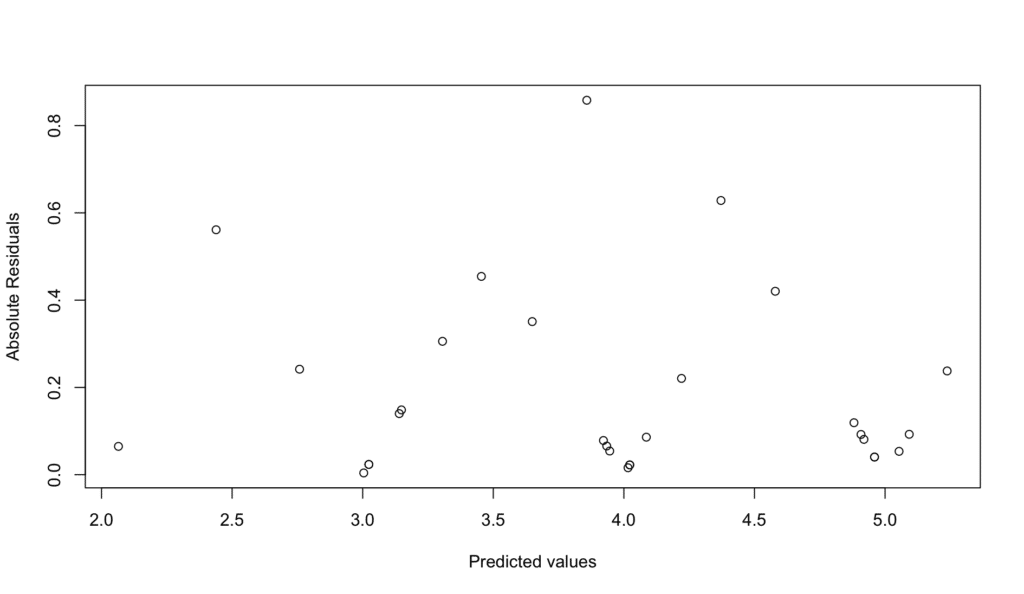ภาพที่ 7: การตรวจสอบ Homoscedasticity - กราฟ Scale-Location

4. Normality of Errors

Residuals ของโมเดลควรมีการแจกแจงแบบปกติโดยประมาณ ซึ่งหมายความว่าหากเราวาดกราฟความถี่ของ Residuals กราฟควรมีรูปร่างคล้ายกับเส้นโค้งรูประฆัง

เพื่อทดสอบ Normality of Errors ใน R ใช้โค้ดต่อไปนี้:

# Check for normality
qqnorm(model$residuals)
qqline(model$residuals)

เราสามารถตรวจสอบสิ่งนี้โดยสร้าง Q-Q Plot จุดควรอยู่บนเส้นแนวทแยงโดยประมาณ

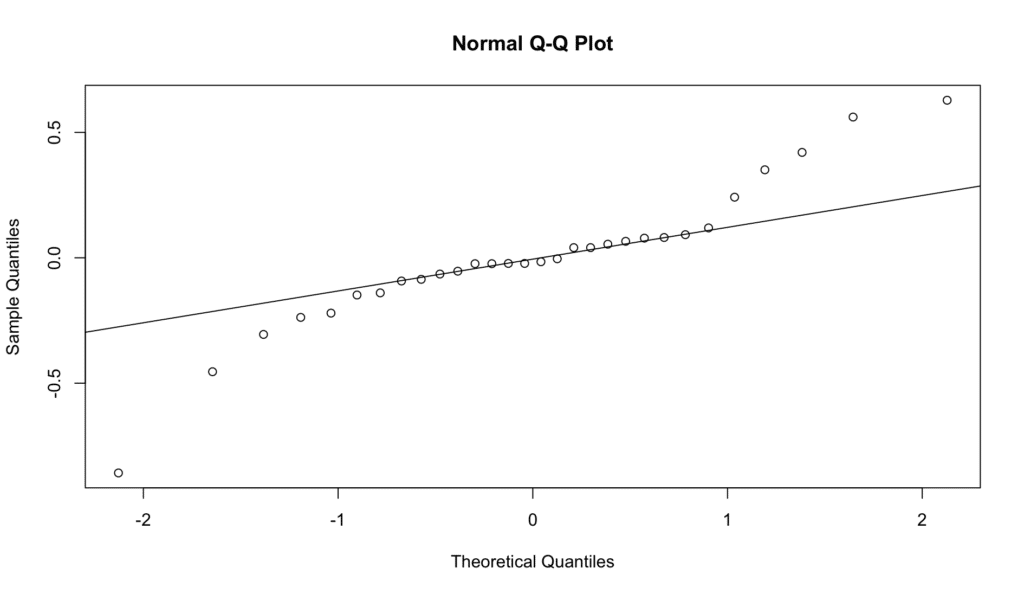ภาพที่ 8: Q-Q Plot สำหรับการทดสอบ Normality of Residuals

5. Absence of Multicollinearity

Predictors ในโมเดลไม่ควรมีความสัมพันธ์อย่างสมบูรณ์กัน สมมติว่ามี Perfect Multicollinearity (หรือแม้แต่ High Multicollinearity) ในกรณีนั้น มันหมายความว่า Predictors สองตัวหรือมากกว่านั้นกำลังให้ข้อมูลเดียวกันแก่เราเกี่ยวกับความแปรปรวนใน Outcome Variable ทำให้ยากต่อการระบุผลกระทบอิสระของ Predictor แต่ละตัว

เราสามารถตรวจสอบ Multicollinearity โดยการคำนวณ Variance Inflation Factors (VIF) สำหรับ Predictors VIFs ที่สูงกว่า 5 บอกถึง High Multicollinearity

นี่คือโค้ดสำหรับทดสอบ VIF ใน R:

# Check for multicollinearity
library(car)
vif(model)

ค่า VIF ในผลลัพธ์ของเราบอกว่าอาจมี Multicollinearity ในชุดข้อมูลจำลองของเรา เนื่องจากค่า VIF ที่มากกว่า 5 หรือ 10 มักถูกใช้เป็นตัวบอกของ High Multicollinearity ซึ่งหมายความว่า Predictors ในโมเดลของเรามีความสัมพันธ์กัน ซึ่งอาจทำให้การตีความผลกระทบของ Predictor แต่ละตัวซับซ้อน

ภาพที่ 9: ค่า VIF สำหรับการประเมิน Multicollinearity

อย่างไรก็ตาม โมเดลของเรารวมถึง Interaction Terms ซึ่งสามารถเพิ่มค่า VIF ดังนั้นค่าสูงเหล่านี้อาจไม่จำเป็นต้องบอกถึงปัญหา มันเป็นสิ่งที่ต้องตระหนักถึง เพราะมันอาจมีอิทธิพลต่อการตีความได้ของ Coefficients ของโมเดล

สำหรับแบบฝึกหัดทางการศึกษานี้ เราจะดำเนินการต่อกับโมเดลของเรา ในบริบทที่ไม่ใช่การศึกษา พิจารณาแก้ไข Multicollinearity ที่รุนแรงด้วยกลยุทธ์เช่นการลบ Predictors บางตัว การรวม Predictors ที่มีความสัมพันธ์ หรือการใช้เทคนิค Regularization

หมายเหตุ: โปรดทราบว่า Multicollinearity ไม่ส่งผลกระทบต่อความสามารถของโมเดลในการคาดการณ์ Dependent Variable มันเพียงแค่ทำให้การตีความ Coefficients ของ Predictors ซับซ้อน หากเป้าหมายหลักคือการคาดการณ์ ไม่ใช่การตีความ Multicollinearity อาจไม่ใช่ความกังวลที่สำคัญ

6. No Influential Outliers

ไม่ควรมี Data Point เดียวที่มีอิทธิพลอย่างมากเกินไปต่อการประมาณค่าของโมเดล แม้ว่า Outliers จะไม่ใช่เรื่องแปลก แต่ Outliers ที่มีอิทธิพลมากเป็นพิเศษสามารถบิดเบือนผลลัพธ์ของโมเดลและลดความแม่นยำของการคาดการณ์ของคุณ

เราสามารถตรวจสอบ Influential Outliers โดยใช้ Cook's Distance โดยมี Cut-Off ที่ใช้กันทั่วไปคือ 4/(n-k-1) ที่ทำเครื่องหมายด้วยเส้นสีแดง โดยที่ n คือจำนวนการสังเกต และ k คือจำนวน Predictors นี่คือสคริปต์ R สำหรับ Cook's Distance:

# Define the threshold
threshold <- 4/length(cooksd)

# Determine the range for y-axis
# Here, we use 1.1 to ensure the maximum value is within the plot area
yrange <- c(0, max(cooksd, threshold)* 1.1)

# Plot Cook's distance with manually set y-axis limits
plot(cooksd, ylim = yrange,
     main = "Influential Observations by Cook's distance",
     pch = 16)

# Add the threshold line
abline(h = threshold, col = "red")

หากการสังเกตทั้งหมดอยู่ต่ำกว่าเส้นสีแดงที่แสดง Threshold ใน Cook's Distance Plot มันบอกว่าไม่มี Influential Outliers ที่โดดเด่นเป็นพิเศษในข้อมูล - เช่นในกรณีของเรา

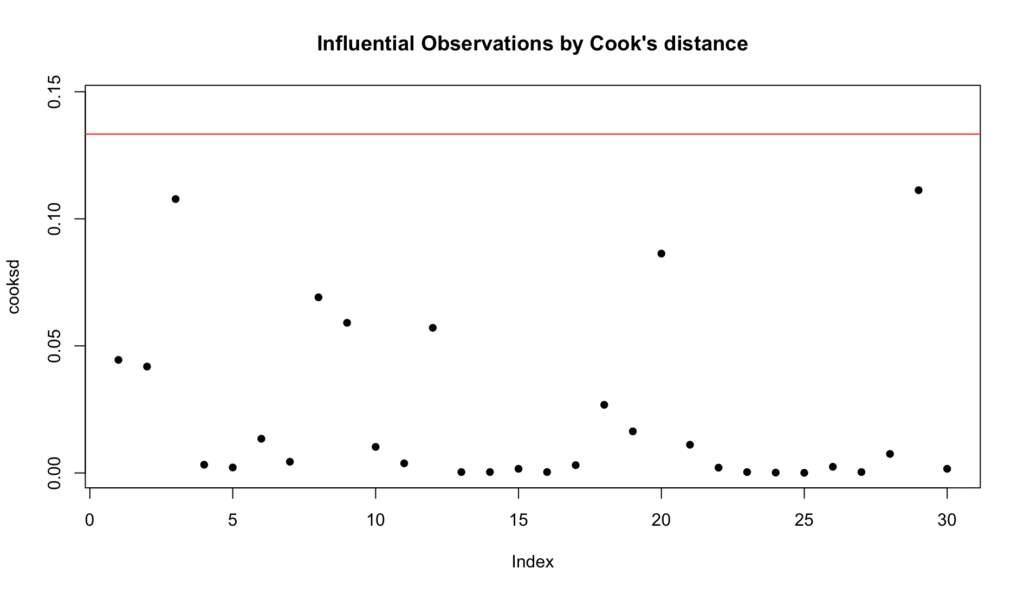ภาพที่ 10: Cook's Distance สำหรับการระบุ Influential Outliers

Influential Outliers สามารถบิดเบือนผลลัพธ์การวิเคราะห์และลดความแม่นยำของการคาดการณ์ที่ทำจากโมเดล ดังนั้น การค้นพบว่าไม่มี Influential Outliers ดังกล่าวช่วยให้มั่นใจในความถูกต้องและความแข็งแกร่งของผลลัพธ์ของ Moderation Analysis

และนี่คือโบนัสของคุณสำหรับการอ่านและฝึกฝนกับเราจนถึงตอนนี้: สคริปต์ R ที่สรุปกราฟวินิจฉัยสี่แบบที่สร้างโดย Function plot() ข้างต้นและบันทึกไว้ใน PDF ชื่อ "model_diagnostic_plots.pdf" ใน Working Directory ของคุณ

# Open the pdf file
pdf("model_diagnostic_plots.pdf")

# Create diagnostic plots
par(mfrow = c(2, 2))
plot(model)

# Close the pdf file
dev.off()

และนี่คือ Output:

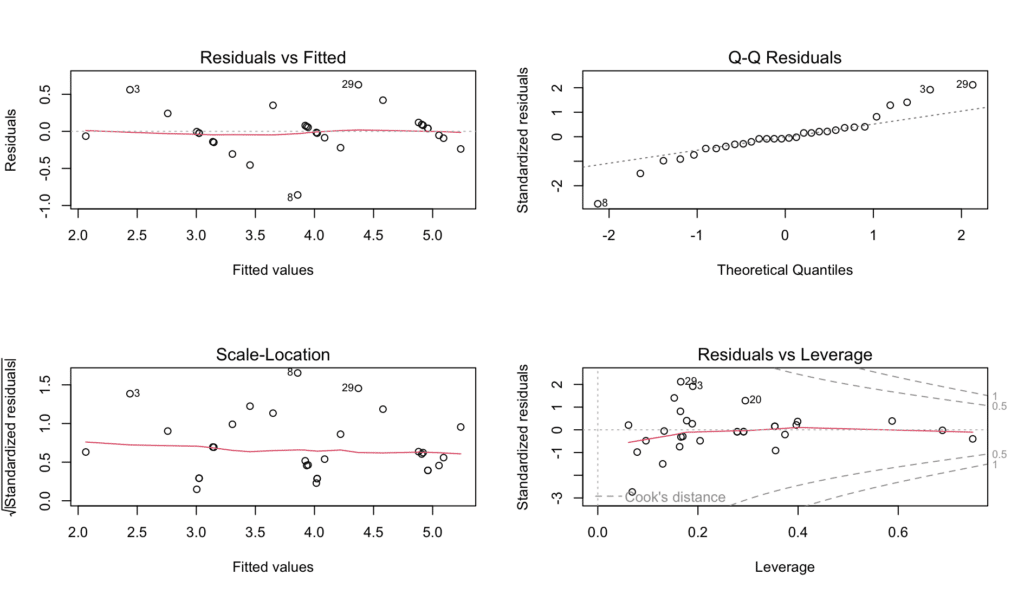ภาพที่ 11: แผง Diagnostic Plots ที่สมบูรณ์ที่สร้างโดย Function plot()

ขั้นตอนที่ 8: การรายงานและอภิปรายผล Multiple Moderation Analysis ในการศึกษาของคุณ

ตอนนี้ที่เราสรุปการวิเคราะห์ของเราแล้ว ก็ถึงเวลาที่จะเรียนรู้วิธีการรายงานและอภิปรายผลการค้นพบในบทความวิจัยของคุณ นี่คือลักษณะที่ควรเป็น:

สำคัญ: เมื่อรายงานและอภิปรายผลลัพธ์ในบทความวิจัย มีแนวทางทั่วไปบางประการที่ควรปฏิบัติตาม:

• ใช้ Past Tense: เนื่องจากการวิจัยได้ดำเนินการแล้วและผลลัพธ์ได้ถูกค้นพบแล้ว มันเป็นมาตรฐานที่จะใช้ Past Tense เมื่ออภิปรายสิ่งเหล่านี้

• หลีกเลี่ยง Personal Pronouns: การใช้ Personal Pronouns (ฉัน, เรา, คุณ) มักไม่แนะนำในการเขียนทางวิชาการ แทนที่จะเป็นเช่นนั้น พยายามเขียนในน้ำเสียงที่เป็นกลางและเป็นทางการมากขึ้น

• ชัดเจนและกระชับ: มันสำคัญที่จะระบุผลการค้นพบของคุณอย่างชัดเจนและกระชับ

• หลีกเลี่ยงความแน่นอนสมบูรณ์: ผลการค้นพบทางวิทยาศาสตร์แทบจะไม่เคยเป็นที่แน่นอน ดังนั้น หลีกเลี่ยงการใช้ "พิสูจน์" หรือ "ยืนยัน" ในการอภิปรายของคุณ ใช้คำว่า "บอกว่า" "ระบุ" หรือ "สนับสนุน"

• ใช้รูปภาพและตารางอย่างเหมาะสม: รูปภาพ ตาราง และการแสดงภาพข้อมูลอื่นๆ สามารถช่วยเป็นอย่างมากในการทำความเข้าใจผลลัพธ์ของคุณ

• อภิปรายในบริบทของวรรณกรรม: เมื่ออภิปรายผลลัพธ์ของคุณ มันสำคัญที่จะเชื่อมโยงพวกมันกลับไปยังการวิจัยก่อนหน้านี้ในสาขา นี่ช่วยให้ผลการค้นพบของคุณอยู่ในบริบทและแสดงว่าพวกมันมีส่วนช่วยต่อกลุ่มความรู้ที่ใหญ่ขึ้นอย่างไร

• พิจารณาข้อจำกัด: การศึกษาทุกครั้งมีข้อจำกัด และมันสำคัญที่จะยอมรับพวกมัน นี่ไม่เพียงแต่เพิ่มความน่าเชื่อถือให้กับงานของคุณ แต่ยังให้แนวทางสำหรับการวิจัยในอนาคต

• แก้ไขสมมติฐาน: หลังจากรายงานผลการค้นพบของคุณ อภิปรายว่าพวกมันเกี่ยวข้องกับสมมติฐานเริ่มต้นของคุณอย่างไร ไม่ว่าข้อมูลของคุณจะสนับสนุนหรือขัดแย้งกับสมมติฐานของคุณ การอภิปรายนี้เป็นกุญแจสำคัญในการปิดวงของคำถามการวิจัยของคุณ

ตัวอย่างส่วนผลลัพธ์:

ในการศึกษาที่ดำเนินการ ผลของการออกกำลังกาย (exercise) ต่อสุขภาพจิต (mental_health) ถูกตรวจสอบ โดยคำนึงถึงบทบาทกำกับที่เป็นไปได้ของคุณภาพการนอนหลับ (sleep_quality) และอาหารที่สมดุล (balanced_diet) วิธีที่เลือกคือ Multiple Moderation Analysis โดยใช้ Ordinary Least Squares (OLS) Regression Model ค่า Variance Inflation Factor (VIF) ซึ่งยังคงต่ำกว่า Threshold ทั่วไปของ 10 หลังจาก Centering Predictors บอกว่า Multicollinearity ถูกจัดการได้อย่างมีประสิทธิภาพ Independence of Errors ถูกตรวจสอบโดยใช้ Durbin-Watson Statistic ซึ่งอยู่ภายในช่วงที่ยอมรับได้ (1.5 ถึง 2.5) Autocorrelation Function (ACF) Plot ถูกตรวจสอบด้วยสายตาเพื่อยืนยันข้อสมมติฐานนี้เพิ่มเติม Residuals ได้รับการตรวจสอบสำหรับ Normality และ Homoscedasticity Q-Q Plot ยืนยันการแจกแจงปกติของ Residuals การตรวจสอบกราฟ Residuals vs Fitted Values เปิดเผยไม่มีรูปแบบที่เห็นได้ชัด บอกว่าข้อสมมติฐานของ Homoscedasticity เป็นจริง Influential Outliers ถูกตรวจสอบโดยใช้ Cook's Distance จุดข้อมูลทั้งหมดถูกพบว่าอยู่ต่ำกว่า Threshold (1.00) บอกว่าไม่มี Outlier ที่มีอิทธิพลมากเกินไป โมเดล Multiple Moderation อธิบายสัดส่วนที่สำคัญของความแปรปรวนในสุขภาพจิต, R² = .9027, F(7, 22) = 29.16, p < 0.001 Predictors แต่ละตัว คือ exercise, sleep_quality และ balanced_diet ไม่ได้คาดการณ์สุขภาพจิตอย่างมีนัยสำคัญ อย่างไรก็ตาม Interaction Terms มีความสัมพันธ์อย่างมีนัยสำคัญกับผลลัพธ์สุขภาพจิต Three-Way Interaction Effect ระหว่าง exercise, sleep_quality และ balanced_diet ไม่มีนัยสำคัญ (B = -0.03971, p = 0.2464) บอกว่า sleep_quality และ balanced_diet รวมกันไม่ได้กำกับความสัมพันธ์ระหว่าง exercise และ mental health อย่างมีนัยสำคัญ การตีความเพิ่มเติมของ Two-Way Interaction Terms บอกว่ามี Moderating Effect ที่มีนัยสำคัญของ sleep_quality ต่อความสัมพันธ์ระหว่าง exercise และ mental health (B = 0.17452, p = 0.0887) ในทางตรงกันข้าม balanced_diet ไม่แสดง Moderating Effect ที่มีนัยสำคัญกับทั้ง exercise (B = 0.05188, p = 0.6160) หรือ sleep_quality (B = 0.06690, p = 0.5713) ผลลัพธ์เหล่านี้ควรตีความด้วยความระมัดระวัง เนื่องจากขนาดตัวอย่างที่เล็กและลักษณะเบื้องต้นของการวิเคราะห์นี้ ความเข้าใจที่ครอบคลุมเกี่ยวกับความสัมพันธ์ที่ซับซ้อนระหว่างตัวแปรเหล่านี้อาจต้องการการวิจัยเพิ่มเติม

ท้ายที่สุด โปรดจำไว้ว่าการวิเคราะห์นี้ดำเนินการบนชุดข้อมูลที่สร้างขึ้นเพื่อวัตถุประสงค์ทางการศึกษา ดังนั้น การควบคุมทางสถิติที่ซับซ้อนกว่าอาจจำเป็น และผลลัพธ์ที่แตกต่างกันอาจเกิดขึ้นกับชุดข้อมูลในโลกแห่งความเป็นจริง

คำถามที่พบบ่อย

สรุป

ในบทเรียนที่ครอบคลุมนี้ คุณได้เรียนรู้วิธีการทำ Multiple Moderation Analysis ใน R ตั้งแต่ต้นจนจบ ตอนนี้คุณเข้าใจแล้วว่า Multiple Moderation Model คืออะไร วิธีการทดสอบ Moderating Effects ที่มีตัวแปรกำกับสองตัวหรือมากกว่านั้น และวิธีการตีความ Three-Way Interactions ใน Moderated Multiple Regression

คุณได้เชี่ยวชาญทักษะที่จำเป็นสำหรับ Moderation Analysis ใน R: การสร้าง Interaction Terms, การสร้าง Moderation Models, การตรวจสอบ Assumptions สำหรับ Moderation Analysis และการแสดงผล Moderating Effects ไม่ว่าคุณจะกำลังทำ Double Moderation Analysis ในการวิจัยทางจิตวิทยาหรือสำรวจ Two Moderators ในการวิเคราะห์ทางธุรกิจ ตอนนี้คุณสามารถทำ Multiple Moderation Analysis และรายงานผลการค้นพบตามมาตรฐานทางวิชาการได้อย่างมั่นใจ

หากคุณพบว่าคู่มือ Moderation ใน R นี้เป็นประโยชน์ สำรวจบทเรียนที่เกี่ยวข้องของเราเกี่ยวกับ How To Run Mediation Analysis in R เพื่อทำความเข้าใจ 'อย่างไร' และ 'ทำไม' ของความสัมพันธ์ ในขณะที่ Moderation Analysis เปิดเผย 'เมื่อใด' และ 'สำหรับใคร'