Pearson Correlation ใน Excel คืออะไร? วิธีคำนวณค่าสหสัมพันธ์ด้วยฟังก์ชัน CORREL [พร้อมตัวอย่าง]

เรียนรู้วิธีคำนวณ Pearson Correlation Coefficient ใน Excel โดยใช้ฟังก์ชัน CORREL และ Data Analysis Toolpak คู่มือทีละขั้นตอนนี้แสดงให้คุณเห็นวิธีวัดความสัมพันธ์ระหว่างตัวแปรสองตัว แปลผลลัพธ์ และตรวจสอบสมมติฐาน

Pearson Correlation Coefficient วัดความแข็งแกร่งและทิศทางของความสัมพันธ์เชิงเส้นระหว่างตัวแปรต่อเนื่องสองตัว ฟังก์ชัน CORREL ในตัวของ Excel ทำให้การคำนวณค่าสหสัมพันธ์ง่ายและรวดเร็ว ไม่ว่าคุณจะวิเคราะห์ค่าใช้จ่ายโฆษณากับรายได้ คะแนนสอบกับชั่วโมงการศึกษา หรือตัวแปรสองตัวที่เกี่ยวข้องกันใดๆ

ดาวน์โหลดชุดข้อมูลฝึกปฏิบัติจาก Sidebar (รหัสผ่าน: uedufy) และปฏิบัติตามตัวอย่าง

Pearson Correlation Coefficient คืออะไร?

สมมติว่าคุณเป็นเจ้าของร้านขายเสื้อผ้าและต้องการดูว่ามีความสัมพันธ์ระหว่างค่าใช้จ่ายในการโฆษณากับรายได้ที่คุณทำได้หรือไม่ นี่คือจุดที่ Pearson Correlation Coefficient มีประโยชน์!

หากค่าสัมประสิทธิ์ใกล้เคียง -1 หมายความว่าเมื่อคุณใช้จ่ายกับการโฆษณามากขึ้น รายได้ของคุณมีแนวโน้มที่จะลดลง และถ้าค่าสัมประสิทธิ์ใกล้เคียง 0 ก็ไม่มีความสัมพันธ์ที่แท้จริงระหว่างการโฆษณาและรายได้

คุณดูข้อมูลของคุณ และ Pearson Correlation Coefficient คือ 0.8 นี่หมายความว่ามีความสัมพันธ์เชิงบวกที่แข็งแกร่งระหว่างการโฆษณาและรายได้: ยิ่งคุณใช้จ่ายกับการโฆษณามากเท่าไหร่ คุณก็ทำเงินได้มากขึ้นเท่านั้น! แต่อย่าตื่นเต้นเกินไปเลย ปัจจัยอื่นๆ ก็สามารถส่งผลต่อรายได้ได้เช่นกัน การรู้ Pearson Correlation Coefficient เป็นเพียงชิ้นส่วนหนึ่งของปริศนา แต่เป็นตัวชี้วัดที่สำคัญที่ต้องพิจารณา

Pearson Correlation Coefficient วัดความแข็งแกร่งของความสัมพันธ์ระหว่างสองสิ่ง ในกรณีนี้คือการโฆษณาและรายได้ ถ้าค่าสัมประสิทธิ์ใกล้เคียง 1 หมายความว่าเมื่อคุณใช้จ่ายกับการโฆษณามากขึ้น คุณอาจเห็นการเพิ่มขึ้นของรายได้

$r=\frac{\sum\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum\left(x_i-\bar{x}\right)^2 \sum\left(y_i-\bar{y}\right)^2}}$

โดยที่:

r คือ Correlation Coefficient
xi คือค่าของตัวแปร x ในตัวอย่าง
x̄ คือค่าเฉลี่ยของค่าตัวแปร x
yi คือค่าของตัวแปร y ในตัวอย่าง
ȳ คือค่าเฉลี่ยของค่าตัวแปร y

สมมติฐานของ Pearson Correlation

ก่อนคำนวณ Pearson Correlation Coefficient ใน Excel ให้ตรวจสอบว่าข้อมูลของคุณตรงตามสมมติฐานเหล่านี้:

1. ตัวแปรต่อเนื่อง (Continuous Variables)

ตัวแปรทั้งสองควรวัดในระดับต่อเนื่อง (Interval หรือ Ratio Level) Pearson Correlation ไม่เหมาะสมสำหรับข้อมูลเชิงหมวดหมู่หรือเชิงอันดับ

ตัวอย่างตัวแปรต่อเนื่อง: ส่วนสูง น้ำหนัก อุณหภูมิ คะแนนสอบ รายได้ เวลา

2. ความเป็นเส้นตรง (Linearity)

ความสัมพันธ์ระหว่างตัวแปรสองตัวควรเป็นเส้นตรง นี่หมายความว่าเมื่อตัวแปรหนึ่งเพิ่มขึ้น ตัวแปรอื่นเพิ่มขึ้น (หรือลดลง) ด้วยอัตราคงที่

วิธีตรวจสอบใน Excel: สร้าง Scatter Plot ของข้อมูลของคุณ ถ้าจุดต่างๆ โดยประมาณเป็นรูปแบบเส้นตรง (ไม่ใช่เส้นโค้ง) สมมติฐานความเป็นเส้นตรงได้รับการตอบสนอง

3. ความเป็นอิสระของการสังเกต (Independence of Observations)

แต่ละการสังเกตควรเป็นอิสระ หมายความว่าค่าของการสังเกตหนึ่งไม่ควรมีอิทธิพลหรือเกี่ยวข้องกับค่าของการสังเกตอื่น

ตัวอย่าง: การวัดบุคคลเดียวกันหลายครั้งละเมิดความเป็นอิสระ แต่ละจุดข้อมูลควรมาจากหัวข้อหรือโอกาสการวัดที่แตกต่างกัน

4. Bivariate Normality

สำหรับการทดสอบนัยสำคัญที่แม่นยำ ตัวแปรทั้งสองควรมีการกระจายแบบ Bivariate Normal อย่างไรก็ตาม Pearson Correlation ค่อนข้างทนทานต่อการละเมิดความเป็นปกติสำหรับขนาดตัวอย่างที่ใหญ่ขึ้น (n > 30)

วิธีตรวจสอบใน Excel: สร้าง Histogram สำหรับแต่ละตัวแปรเพื่อประเมินความเป็นปกติด้วยสายตา สำหรับตัวอย่างที่น้อยกว่า 30 พิจารณาใช้การทดสอบความเป็นปกติ

จะเกิดอะไรขึ้นถ้าสมมติฐานถูกละเมิด?

ถ้าข้อมูลของคุณละเมิดสมมติฐานเหล่านี้ (โดยเฉพาะความเป็นเส้นตรงหรือความเป็นปกติ) พิจารณาใช้ Spearman's Rank Correlation Coefficient แทน ซึ่งเป็นทางเลือกแบบ Non-parametric ที่ไม่ต้องการสมมติฐานที่เข้มงวดเหล่านี้

วิธีที่ 1: คำนวณ Correlation Coefficient ใน Excel โดยใช้ฟังก์ชัน CORREL

กลับไปที่ตัวอย่างร้านขายเสื้อผ้าของเราและเรียนรู้วิธีคำนวณ Pearson Correlation Coefficient ใน Excel เพื่อหาว่ามีความสัมพันธ์ระหว่างค่าใช้จ่ายในการโฆษณากับรายได้ที่เราทำได้หรือไม่

1. เตรียมข้อมูลของคุณ: จัดระเบียบข้อมูลของคุณเป็นสองคอลัมน์ โดยแต่ละคอลัมน์แทนตัวแปรสองตัวที่คุณต้องการวิเคราะห์ ในชุดข้อมูลของฉัน ตัวแปรสองตัวที่เราต้องการตรวจสอบว่ามีความสัมพันธ์กันหรือไม่คือ Advertising และ Revenue

ชุดข้อมูล Pearson Correlation Coefficient ใน Excel แสดงสองคอลัมน์สำหรับตัวแปร Advertising และ Revenue ตัวอย่างตัวแปรสองตัวสำหรับการคำนวณ Correlation Coefficient ใน Excel

2. เลือกเซลล์: เลือกเซลล์ในเวิร์กชีตของคุณที่คุณต้องการให้แสดงผลลัพธ์ของ Pearson Correlation Coefficient

เวิร์กชีต Excel พร้อมเซลล์ที่เลือกสำหรับแสดงผลลัพธ์ Pearson Correlation Coefficient เลือกเซลล์ในเวิร์กชีตสำหรับผลลัพธ์ Correlation

3. ใส่ฟังก์ชัน Correlation: พิมพ์ "=CORREL(" ตามด้วยช่วงของคอลัมน์แรกของข้อมูล เครื่องหมายจุลภาค และช่วงของคอลัมน์ที่สองของข้อมูล และปิดวงเล็บ ตัวอย่างเช่น ถ้าข้อมูลของคุณอยู่ในคอลัมน์ B และ C (เหมือนในภาพด้านล่าง) ฟังก์ชัน Correlation จะมีลักษณะดังนี้: =CORREL(B2:B13, C2:C13)

Excel แสดงไวยากรณ์ฟังก์ชัน CORREL สำหรับการคำนวณ Pearson Correlation Coefficient ฟังก์ชัน CORREL ใน Excel

4. คำนวณผลลัพธ์: กดปุ่ม ENTER เพื่อคำนวณ Pearson Correlation Coefficient ผลลัพธ์จะแสดงในเซลล์ที่เลือก Correlation Coefficient ระหว่าง Advertising และ Revenue ในชุดข้อมูลของเราคือ 0.9

Excel แสดงผลลัพธ์ Pearson Correlation Coefficient เป็น 0.9 ผลลัพธ์ Pearson Correlation Coefficient สำหรับตัวแปรที่เลือก

วิธีที่ 2: คำนวณ Correlation Coefficient โดยใช้เครื่องมือ Analysis ใน Excel

นี่คืออีกวิธีหนึ่งในการคำนวณความสัมพันธ์ระหว่างตัวแปรสองตัวใน Excel โดยใช้ Data Analysis Toolpak

1. เตรียมข้อมูลของคุณ: ตรวจสอบให้แน่ใจว่าข้อมูลของคุณจัดระเบียบเป็นสองคอลัมน์ แต่ละคอลัมน์แทนตัวแปร (เหมือนที่เราทำก่อนหน้านี้)

2. ติดตั้งเครื่องมือ Data Analysis ใน Excel: ถ้าคุณไม่เห็นไอคอน Data Analysis ในแท็บ Data ใน Excel คุณควร ติดตั้ง Data Analysis Toolpak ก่อน

Ribbon ของ Excel แสดงตำแหน่งปุ่ม Data Analysis ในแท็บ Data ตำแหน่ง Data Analysis ใน Excel

3. เปิดเครื่องมือ Data Analysis: จากแท็บ Data คลิก Data Analysis และเลือก Correlation

กล่องโต้ตอบ Data Analysis ของ Excel พร้อมตัวเลือก Correlation ที่เลือก Data Analysis - Correlation

4. เลือกข้อมูล: ในกล่องโต้ตอบ Data Analysis เลือก Input Range ซึ่งเป็นช่วงของสองคอลัมน์ของข้อมูล ถ้าคุณรวมป้ายกำกับคอลัมน์ในการเลือกของคุณ (Advertising และ Revenue) ให้ทำเครื่องหมายที่กล่อง Labels in First Row

หมายเหตุ: ในส่วน "Output Options" คุณยังสามารถเลือกได้ว่าคุณต้องการให้ผลลัพธ์แสดงที่ไหน ไม่ว่าจะในเวิร์กชีตใหม่หรือในช่วงของเซลล์ มาปล่อยการตั้งค่าเริ่มต้นไว้ตอนนี้

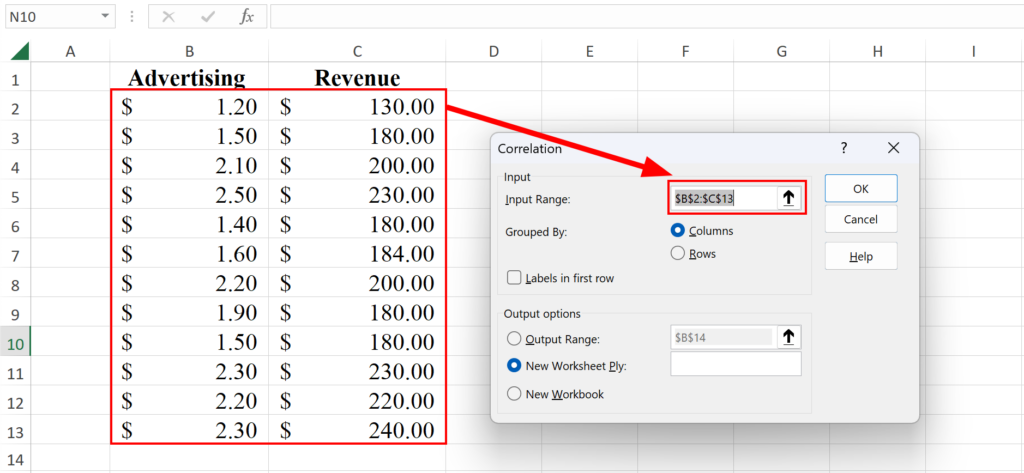กล่องโต้ตอบ Correlation ของ Excel แสดงการเลือก Input Range สำหรับข้อมูล Advertising และ Revenue เลือกช่วงของค่าสำหรับ Correlation

5. เรียกใช้การวิเคราะห์: คลิก OK เพื่อคำนวณ ผลลัพธ์ของ Pearson Correlation Coefficient จะแสดงในตำแหน่ง Output ที่คุณเลือก ตามที่คาดไว้ สำหรับชุดข้อมูลเดียวกัน ค่าสัมประสิทธิ์ก็เท่ากัน: 0.9

Output ของ Excel แสดงผลลัพธ์ Pearson Correlation Coefficient เป็น 0.9 โดยใช้ Data Analysis Toolpak ผลลัพธ์ Pearson Correlation Coefficient ใน Excel

วิธีการแปลผล Pearson Correlation

Pearson Correlation Coefficient (r) จะเป็นค่าระหว่าง -1 และ 1 เสมอ นี่คือวิธีการแปลผลลัพธ์ใน Excel:

การทำความเข้าใจค่า Correlation

ค่าสัมประสิทธิ์:

r = 1: Correlation เชิงบวกที่สมบูรณ์แบบ (เมื่อตัวแปรหนึ่งเพิ่มขึ้น อีกตัวก็เพิ่มขึ้นตามสัดส่วน)
r = -1: Correlation เชิงลบที่สมบูรณ์แบบ (เมื่อตัวแปรหนึ่งเพิ่มขึ้น อีกตัวก็ลดลงตามสัดส่วน)
r = 0: ไม่มี Linear Correlation (ไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปร)

ทิศทาง:

Correlation เชิงบวก (0 ถึง 1): ตัวแปรทั้งสองเคลื่อนไปในทิศทางเดียวกัน
Correlation เชิงลบ (0 ถึง -1): ตัวแปรเคลื่อนไปในทิศทางตรงกันข้าม

การแปลความแข็งแกร่งของ Correlation

ใช้แนวทางเหล่านี้เพื่อแปลความแข็งแกร่งของ Pearson Correlation Coefficient ของคุณ:

ค่า Correlation	ความแข็งแกร่ง	การแปลผล
0.9 ถึง 1.0 (หรือ -0.9 ถึง -1.0)	แข็งแกร่งมาก	ตัวแปรมีความสัมพันธ์กันสูง
0.7 ถึง 0.9 (หรือ -0.7 ถึง -0.9)	แข็งแกร่ง	มีความสัมพันธ์ที่แข็งแกร่ง
0.4 ถึง 0.7 (หรือ -0.4 ถึง -0.7)	ปานกลาง	ความสัมพันธ์ปานกลาง
0.1 ถึง 0.4 (หรือ -0.1 ถึง -0.4)	อ่อนแอ	ความสัมพันธ์อ่อนแอ
0 ถึง 0.1 (หรือ 0 ถึง -0.1)	ไม่มี	ไม่มี Correlation ที่มีความหมาย

ตัวอย่างการแปลผล

ในตัวอย่างของเรา Correlation Coefficient ที่ r = 0.9 บ่งชี้ถึง Correlation เชิงบวกที่แข็งแกร่งมาก ระหว่างตัวแปร Advertising และ Revenue

ความหมาย:

เมื่อค่าใช้จ่ายโฆษณาเพิ่มขึ้น 1 หน่วย รายได้มีแนวโน้มที่จะเพิ่มขึ้นในอัตราที่สม่ำเสมอมาก
81% ของความแปรปรวนในรายได้สามารถอธิบายได้ด้วยค่าใช้จ่ายโฆษณา (คำนวณเป็น r² = 0.9² = 0.81)
นี่เป็นความสัมพันธ์ที่แข็งแกร่งมาก แต่มันไม่ได้พิสูจน์เหตุและผล

สำคัญ: Correlation กับ Causation

คำเตือนที่สำคัญ: Pearson Correlation Coefficient ที่สูงไม่ได้หมายความว่าตัวแปรหนึ่งทำให้เกิดอีกตัวหนึ่ง มันแสดงเพียงว่าพวกมันมีแนวโน้มที่จะเปลี่ยนแปลงไปด้วยกัน

ทำไมสิ่งนี้ถึงสำคัญ:

Correlation แสดงความสัมพันธ์ ไม่ใช่เหตุและผล
ตัวแปรที่สามอาจส่งผลต่อตัวแปรทั้งสอง
ความสัมพันธ์อาจเป็นเรื่องบังเอิญ
Reverse Causation อาจมีอยู่ (B ทำให้เกิด A ไม่ใช่ A ทำให้เกิด B)

เพื่อสร้างเหตุและผล คุณต้องการการออกแบบการวิจัยแบบทดลองหรือวิธีทางสถิติเพิ่มเติม เช่น Regression Analysis

Pearson กับ Spearman Correlation: ใช้อันไหน?

เมื่อวิเคราะห์ Correlation ใน Excel คุณอาจสงสัยว่าควรใช้ Pearson หรือ Spearman Correlation นี่คือวิธีเลือกวิธีที่ถูกต้อง:

Pearson Correlation Coefficient

ใช้ Pearson เมื่อ:

ตัวแปรทั้งสองเป็นแบบต่อเนื่อง (Interval หรือ Ratio Scale)
ความสัมพันธ์ระหว่างตัวแปรเป็นเส้นตรง
ข้อมูลมีการกระจายแบบปกติโดยประมาณ
ไม่มีค่าผิดปกติที่สำคัญ

ข้อดี:

การทดสอบทางสถิติที่มีพลังมากกว่า (ดีกว่าในการตรวจจับ Correlation ที่แท้จริง)
รับรู้และรายงานกันทั่วไปในการวิจัย
ง่ายต่อการคำนวณใน Excel โดยใช้ฟังก์ชัน CORREL

ข้อเสีย:

ไวต่อค่าผิดปกติ
ต้องการสมมติฐาน (ความเป็นเส้นตรง ความเป็นปกติ)
ตรวจจับเฉพาะความสัมพันธ์เชิงเส้น

Spearman Correlation Coefficient

ใช้ Spearman เมื่อ:

ตัวแปรเป็นเชิงอันดับ (Ranked Data)
ความสัมพันธ์เป็นแบบ Monotonic แต่ไม่จำเป็นต้องเป็นเส้นตรง
ข้อมูลมีค่าผิดปกติ
ข้อมูลไม่มีการกระจายแบบปกติ

ข้อดี:

Non-parametric (ไม่ต้องการสมมติฐานการกระจาย)
ทนทานต่อค่าผิดปกติ
ทำงานกับข้อมูลแบบอันดับ/เชิงอันดับ
ตรวจจับความสัมพันธ์แบบ Monotonic (ไม่เพียงแค่เชิงเส้น)

ข้อเสีย:

มีพลังน้อยกว่า Pearson เมื่อสมมติฐานตรงตาม
ซับซ้อนกว่าในการคำนวณใน Excel (ต้องจัดอันดับข้อมูลก่อน)
อาจพลาดความละเอียดของความสัมพันธ์บางอย่าง

คู่มือการตัดสินใจอย่างรวดเร็ว

เลือก Pearson Correlation ถ้า:

ข้อมูลของคุณต่อเนื่องและมีการกระจายแบบปกติ
Scatter Plot แสดงรูปแบบเส้นตรงโดยประมาณ
คุณไม่มีค่าผิดปกติสุดโต่ง

เลือก Spearman Correlation ถ้า:

ข้อมูลของคุณเป็นเชิงอันดับ/จัดอันดับ
Scatter Plot แสดงรูปแบบโค้งหรือไม่เป็นเส้นตรง
คุณมีค่าผิดปกติที่สำคัญ
ข้อมูลของคุณละเมิดสมมติฐานความเป็นปกติ

ตัวอย่าง: ถ้าคุณกำลังทำ Correlation ระหว่างคะแนนสอบ (ต่อเนื่อง มีการกระจายแบบปกติ) กับชั่วโมงการศึกษา (ต่อเนื่อง) ให้ใช้ Pearson ถ้าคุณกำลังทำ Correlation ระหว่างการจัดอันดับความพึงพอใจของลูกค้า (เชิงอันดับ: 1-5 ดาว) กับการให้คะแนนคุณภาพผลิตภัณฑ์ ให้ใช้ Spearman

สำหรับผู้ใช้ Excel ส่วนใหญ่ที่ทำงานกับข้อมูลต่อเนื่องที่มีการกระจายแบบปกติ Pearson Correlation เป็นตัวเลือกที่เหมาะสม

คำถามที่พบบ่อย

Pearson Correlation Coefficient คืออะไร?

Pearson Correlation Coefficient (เรียกอีกอย่างว่า Pearson's r) เป็นตัววัดทางสถิติที่คำนวณความแข็งแกร่งและทิศทางของความสัมพันธ์เชิงเส้นระหว่างตัวแปรต่อเนื่องสองตัว มันมีช่วงตั้งแต่ -1 ถึง +1 โดยที่ -1 บ่งชี้ Correlation เชิงลบที่สมบูรณ์แบบ, +1 บ่งชี้ Correlation เชิงบวกที่สมบูรณ์แบบ และ 0 บ่งชี้ว่าไม่มี Linear Correlation

วิธีแปลผล Pearson Correlation ใน Excel อย่างไร?

แปลผลค่า Pearson Correlation ดังนี้: 0.7 ถึง 1.0 (หรือ -0.7 ถึง -1.0) บ่งชี้ Correlation ที่แข็งแกร่ง, 0.4 ถึง 0.7 (หรือ -0.4 ถึง -0.7) บ่งชี้ Correlation ปานกลาง, 0.1 ถึง 0.4 (หรือ -0.1 ถึง -0.4) บ่งชี้ Correlation อ่อนแอ และ 0 ถึง 0.1 (หรือ 0 ถึง -0.1) บ่งชี้ว่าไม่มี Correlation ค่าบวกหมายความว่าตัวแปรเพิ่มขึ้นด้วยกัน ในขณะที่ค่าลบหมายความว่าหนึ่งเพิ่มขึ้นเมื่ออีกตัวลดลง

ความแตกต่างระหว่าง Pearson และ Spearman Correlation คืออะไร?

Pearson Correlation วัดความสัมพันธ์เชิงเส้นระหว่างตัวแปรต่อเนื่องและสันนิษฐาน Bivariate Normality Spearman Correlation เป็นการทดสอบแบบ Non-parametric ที่วัดความสัมพันธ์แบบ Monotonic (ไม่จำเป็นต้องเป็นเส้นตรง) และทำงานกับข้อมูลแบบอันดับหรือเชิงอันดับ ใช้ Pearson เมื่อข้อมูลของคุณมีการกระจายแบบปกติและความสัมพันธ์เป็นเส้นตรง ใช้ Spearman เมื่อข้อมูลไม่มีการกระจายแบบปกติหรือมีค่าผิดปกติ

Pearson Correlation สามารถพิสูจน์เหตุและผลได้หรือไม่?

ไม่ได้ Pearson Correlation ไม่ได้พิสูจน์เหตุและผล มันวัดเพียงความแข็งแกร่งและทิศทางของความสัมพันธ์ระหว่างตัวแปรสองตัว Correlation ที่สูงหมายความว่าตัวแปรมีแนวโน้มที่จะเปลี่ยนแปลงไปด้วยกัน แต่มันไม่ได้บอกคุณว่าตัวแปรไหนทำให้เกิดการเปลี่ยนแปลงในอีกตัว หรือถ้าตัวแปรที่สามส่งผลต่อทั้งสอง เพื่อสร้างเหตุและผล คุณต้องการการออกแบบการวิจัยแบบทดลองหรือวิธีทางสถิติเพิ่มเติมเช่น Regression Analysis

ฉันต้องการขนาดตัวอย่างเท่าไหร่สำหรับ Pearson Correlation ใน Excel?

แม้ว่า Pearson Correlation จะสามารถคำนวณได้ด้วยตัวอย่างเล็กๆ แต่คุณต้องการอย่างน้อย n=30 สำหรับผลลัพธ์ที่เชื่อถือได้และการทดสอบนัยสำคัญ ตัวอย่างที่เล็กกว่า (n<30) ไวต่อค่าผิดปกติและการละเมิดสมมติฐานความเป็นปกติมากกว่า สำหรับการตรวจจับ Correlation เล็กๆ (r=0.1-0.3) คุณอาจต้องการ 100+ การสังเกตสำหรับพลังทางสถิติที่เพียงพอ

วิธีคำนวณ p-value สำหรับ Pearson Correlation ใน Excel อย่างไร?

ฟังก์ชัน CORREL ของ Excel คำนวณเฉพาะ Correlation Coefficient ไม่ใช่ p-value เพื่อรับ p-value คุณต้องใช้เครื่องมือ Correlation ของ Data Analysis Toolpak (ซึ่งก็ไม่ได้ให้ p-value โดยตรงเช่นกัน) หรือคำนวณด้วยตนเองโดยใช้ฟังก์ชัน T.DIST ด้วยสูตร: t = r × sqrt((n-2)/(1-r²)) โดยที่ r คือ Correlation Coefficient และ n คือขนาดตัวอย่าง

Correlation ที่ 0.9 หมายความว่าอย่างไร?

Correlation ที่ 0.9 บ่งชี้ถึงความสัมพันธ์เชิงบวกเชิงเส้นที่แข็งแกร่งมากระหว่างตัวแปรสองตัว นี่หมายความว่าเมื่อตัวแปรหนึ่งเพิ่มขึ้น ตัวแปรอื่นมีแนวโน้มที่จะเพิ่มขึ้นในอัตราที่สม่ำเสมอมาก อย่างไรก็ตาม จำไว้ว่าแม้แต่ Correlation 0.9 ก็หมายความว่าเพียง 81% (0.9²) ของความแปรปรวนในตัวแปรหนึ่งสามารถอธิบายได้ด้วยตัวแปรอื่น - ยังมี 19% ของความแปรปรวนที่ไม่ได้อธิบาย

สรุป

Pearson Correlation Coefficient เป็นเครื่องมือที่มีประโยชน์สำหรับการทำความเข้าใจความสัมพันธ์ระหว่างตัวแปรสองตัว และมันง่ายต่อการคำนวณใน Excel โดยใช้ Data Analysis Toolpak หรือฟังก์ชัน CORREL