Regresia Liniară Multiplă în SPSS: Ghid Complet [2026]

•By Leonard Cucos•ro
Teste StatisticeTutoriale SPSSAnalize Avansate

Regresia liniară multiplă este una dintre cele mai puternice tehnici statistice pentru analizarea relației dintre multiple variabile independente și o singură variabilă dependentă. În acest ghid cuprinzător, vei învăța cum să rulezi regresia multiplă în SPSS, cum să interpretezi output-ul regresiei multiple în SPSS și să înțelegi fiecare componentă a rezultatelor analizei.

Indiferent dacă investighezi eficacitatea marketingului, prezici performanța academică sau analizezi orice relație cu multipli predictori, acest tutorial acoperă totul, de la prepararea datelor până la interpretarea rezultatelor. Îți voi furniza un set complet de date SPSS pentru analiza regresiei liniare multiple astfel încât să poți urma pas cu pas.

Analiza regresiei multiple în SPSS este directă. Dacă știi cum să calculezi o regresie liniară simplă, vei găsi procesul aproape identic. Diferența principală este interpretarea rezultatelor cu multipli predictori, și vom acoperi fiecare parametru în detaliu.

Ce este Regresia Liniară Multiplă Explicată cu Exemplu

Cu regresia liniară simplă, analizăm relația cauzală între o singură variabilă independentă și o variabilă dependentă. Cu alte cuvinte, ne propunem să vedem dacă variabila independentă (predictor) are un efect semnificativ asupra variabilei dependente (rezultat). Dar cum analizăm regresia când un model conține multiple variabile independente?

Salutați analiza de regresie liniară multiplă.

În analiza de regresie liniară multiplă, testăm efectul a doi sau mai mulți predictori asupra variabilei rezultat, de unde și termenul de regresie liniară multiplă.

Diagramă conceptuală arătând multiple variabile independente indicând către o variabilă dependentă

Regresia liniară multiplă analizează relația dintre multipli predictori și un rezultat

În termeni de analiză, atât pentru regresia liniară simplă, cât și pentru cea multiplă, obiectivul rămâne în mare măsură același: găsirea dacă există vreo semnificație (valoarea P) între multiplii predictori și rezultat. Dacă valoarea P este egală sau mai mică decât 0.05 (P ≤ 0.05), relația predictor-rezultat este semnificativă.

Să aruncăm o privire la un exemplu de regresie liniară multiplă. Să presupunem că vrem să investigăm relația dintre eforturile de marketing și intenția de cumpărare a consumatorilor unei companii. În acest caz, variabila predictor este eforturile de marketing, iar rezultatul este intenția de cumpărare.

Știu la ce te gândești. "Eforturile de marketing" este un termen atât de larg și atât de mulți factori pot contribui la el. Nu are sens să investighezi eforturile de marketing în ansamblu dacă nu poți identifica care factori sunt mai importanți decât alții, corect?

Să împărțim eforturile de marketing în mai multe variabile independente (X), de exemplu, content marketing (X1), social media marketing (X2) și email marketing (X3). Iată cum arată cadrul conceptual pentru acest exemplu:

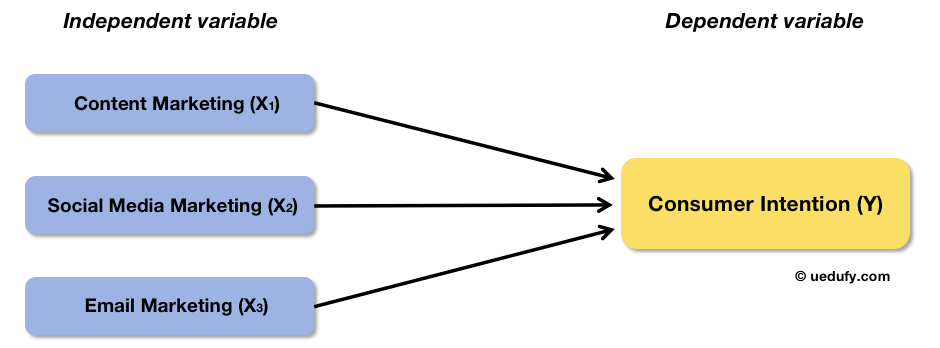
Cadru conceptual arătând content marketing, social media marketing și email marketing ca predictori ai intenției de cumpărare a consumatorilor

Exemplu de cadru conceptual: Eforturi de marketing împărțite în trei predictori

Acum că avem cadrul nostru conceptual, să trecem la acțiune și să facem analiza de regresie multiplă în SPSS folosind exemplul discutat mai sus.

Calculează Regresia Liniară Multiplă folosind SPSS

Calcularea regresiei liniare multiple folosind SPSS este foarte asemănătoare cu efectuarea unei analize de regresie liniară simplă în SPSS. Dacă vrei să urmărești, descarcă setul de date SPSS din secțiunea Download din bara laterală.

Setul de date SPSS exemplu conține 30 de eșantioane unde Content, SocialMedia, Email sunt variabilele independente (predictori), iar Consumer_Intention este variabila dependentă (rezultat). După descărcare, dezarhivează fișierul și dă dublu-click pe fișierul cu extensia .sav pentru a importa setul de date în SPSS.

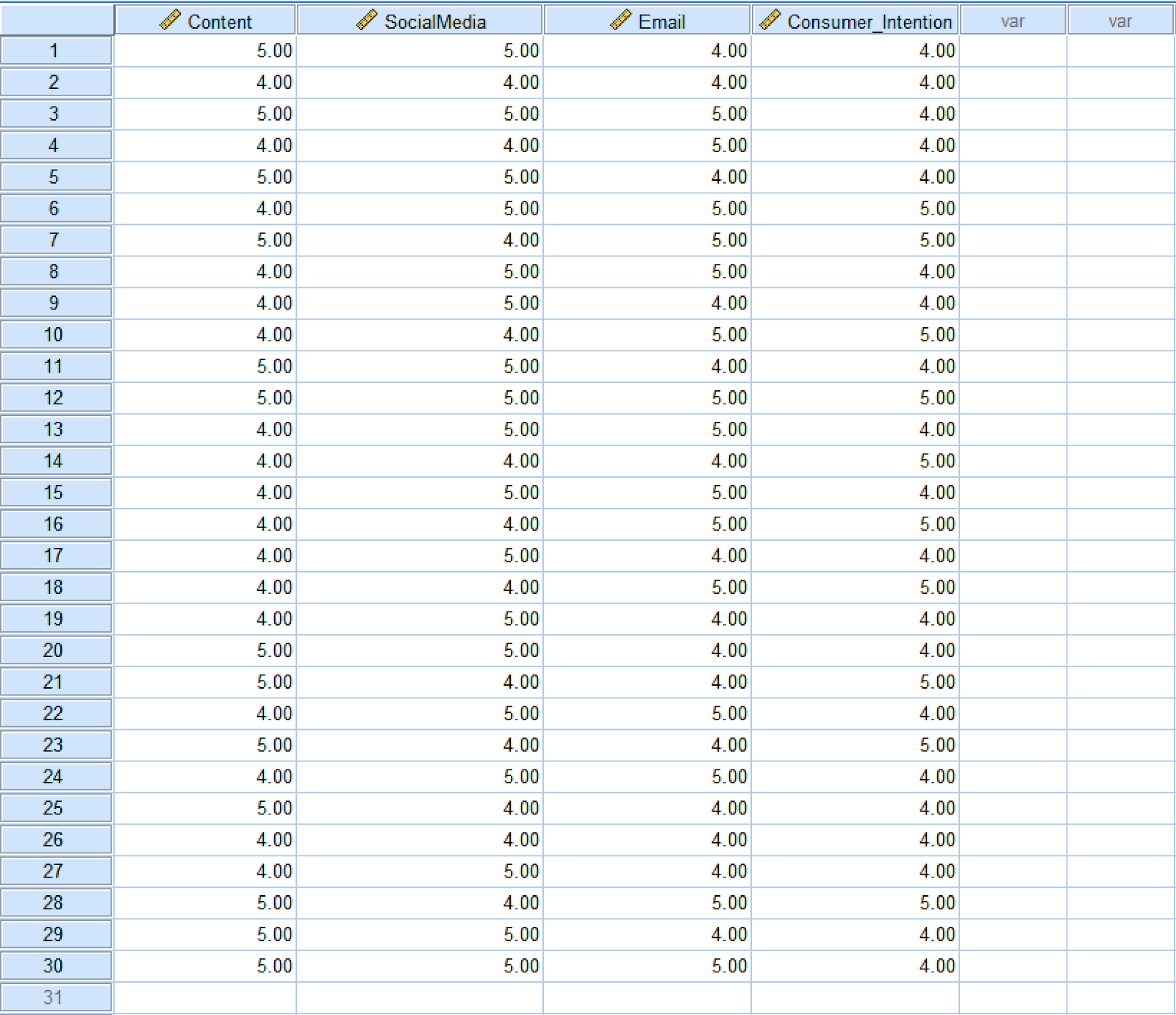
SPSS Data View arătând setul de date cu coloane pentru variabilele Content, SocialMedia, Email și Consumer_Intention

Set de date exemplu cu trei predictori și o variabilă rezultat

Următorul pas, să învățăm cum să calculăm regresia liniară multiplă folosind SPSS pentru acest exemplu.

  1. În meniul superior SPSS, mergi la Analyze → Regression → Linear.

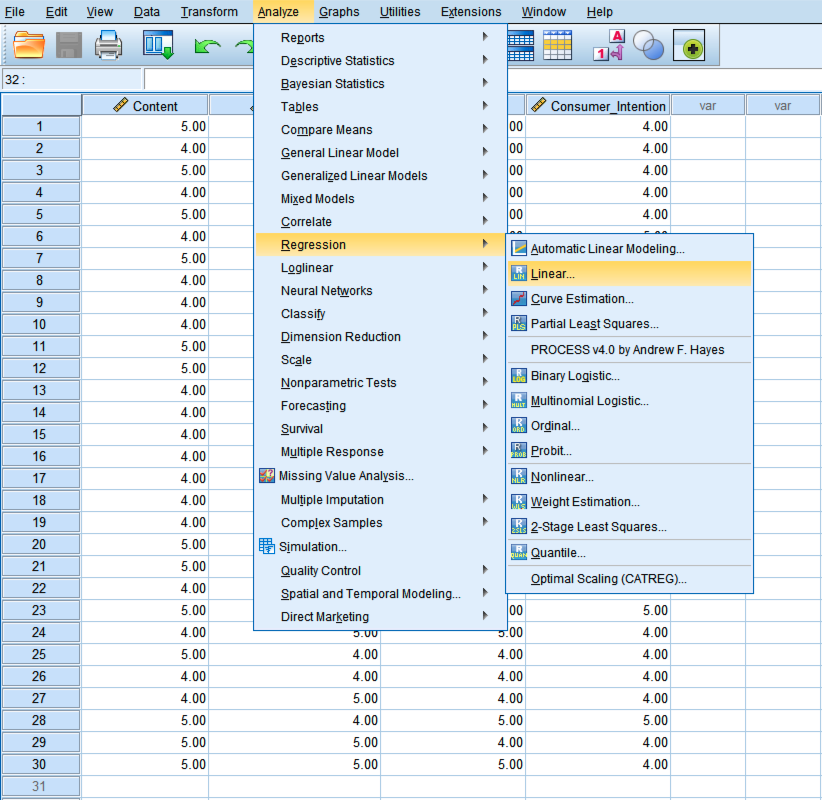
Meniul SPSS cu calea Analyze, Regression, Linear evidențiată

Navighează la Analyze → Regression → Linear în SPSS

  1. În fereastra Linear Regression, folosește butonul săgeată pentru a muta rezultatul Consumer_Intention în caseta Dependent. Fă același lucru cu variabilele predictor Email, Content și SocialMedia pentru a le muta în caseta Independent(s).

Asigură-te că metoda de regresie liniară este setată pe Enter.

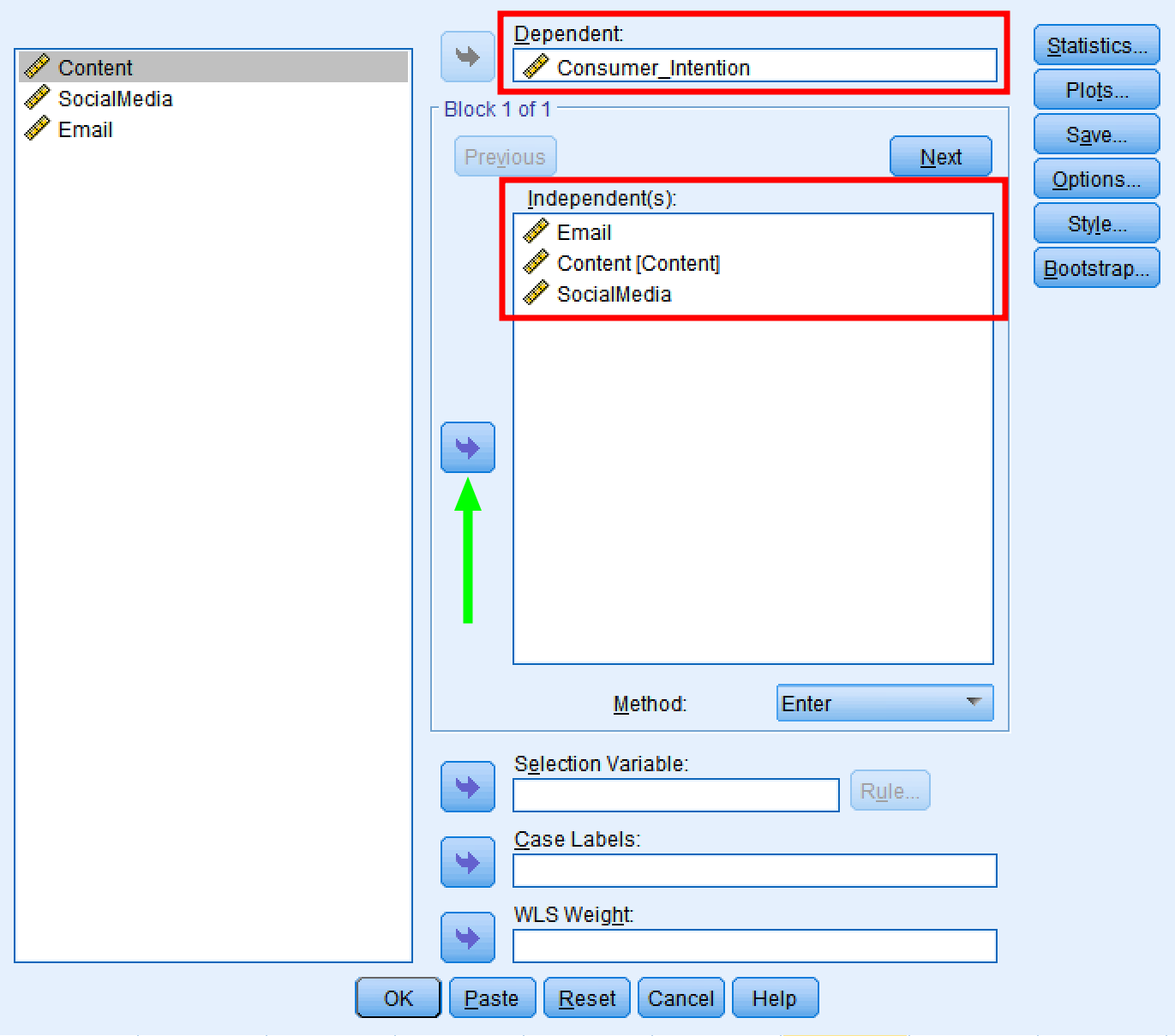
Caseta de dialog SPSS Linear Regression arătând selecția variabilelor cu Consumer_Intention ca dependentă și trei predictori ca variabile independente

Selectează variabilele dependente și independente în dialogul Linear Regression

  1. Dă click pe butonul OK pentru a calcula regresia liniară multiplă folosind SPSS. O fereastră nouă conținând rezultatele regresiei liniare multiple va apărea.

Interpretează Output-ul Regresiei Liniare Multiple în SPSS

Acum că avem rezultatele regresiei liniare multiple în SPSS, să ne uităm cum să interpretăm output-ul. Implicit, SPSS va afișa patru tabele în output-ul regresiei:

  • Variables Entered/Removed
  • Model Summary
  • ANOVA
  • Coefficients

Să aruncăm o privire la fiecare tabel și să înțelegem ce înseamnă acei termeni și valori.

Variables Entered/Removed

Acest tabel conține un rezumat al analizei regresiei liniare multiple folosind SPSS, respectiv modelul de regresie folosit, variabilele independente și dependente introduse în analiză, precum și metoda de regresie.

În unele cazuri, SPSS va alege să elimine variabile din model dacă se găsesc că cauzează probleme de multicoliniaritate. În această analiză de regresie, nu au fost eliminate variabile, prin urmare putem deduce că nu au fost găsite variabile care să fie liniar dependente una de alta.

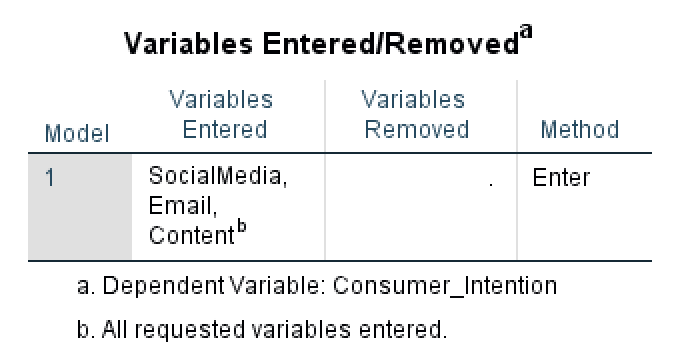
Tabel de output SPSS arătând Variables Entered/Removed cu toți cei trei predictori introduși și niciunul eliminat

Tabelul Variables Entered/Removed arată rezumatul modelului

Model Summary

Tabelul Model Summary oferă statistici cheie despre cât de bine se potrivește modelul de regresie cu datele. Acest tabel include trei măsuri critice: R, R² și Adjusted R².

R (Coeficientul de Corelație Multiplă) reprezintă corelația dintre valorile observate și valorile prezise ale variabilei dependente. Variază de la 0 la 1, cu valori mai mari indicând predicție mai bună. În exemplul nostru, R indică forța relației dintre toți cei trei predictori combinați și Consumer_Intention.

R² (Coeficientul de Determinare) ne spune proporția varianței în variabila dependentă care este explicată de variabilele independente. Este calculat ca:

R2=SSRSST=Suma Pa˘tratelor de RegresieSuma Totala˘ a Pa˘tratelorR^2 = \frac{SSR}{SST} = \frac{\text{Suma Pătratelor de Regresie}}{\text{Suma Totală a Pătratelor}}

În cazul nostru:

R2=2.9526.667=0.443 sau 44.3%R^2 = \frac{2.952}{6.667} = 0.443 \text{ sau } 44.3\%

Aceasta înseamnă că cei trei predictori ai noștri (Email, Content, SocialMedia) explică 44.3% din variația în Consumer_Intention. Restul de 55.7% este varianță neexplicată.

Adjusted R² modifică R² pentru a ține cont de numărul de predictori din model. Este mai precis pentru compararea modelelor cu număr diferit de predictori deoarece penalizează adăugarea de variabile inutile. Formula este:

Adjusted R2=1−(1−R2)(n−1)n−k−1\text{Adjusted } R^2 = 1 - \frac{(1-R^2)(n-1)}{n-k-1}

Unde:

  • n = dimensiunea eșantionului (30 în cazul nostru)
  • k = numărul de predictori (3 în cazul nostru)

Adjusted R² va fi întotdeauna ușor mai mic decât R², în special cu dimensiuni mai mici ale eșantionului sau mai mulți predictori. Când compari modele, preferă-l pe cel cu Adjusted R² mai mare.

ANOVA

Tabelul ANOVA în regresia multiplă testează dacă modelul de regresie în ansamblu explică în mod semnificativ varianța în variabila dependentă. Compară varianța explicată de model (Regression) împotriva varianței neexplicate (Residual). Dacă modelul explică semnificativ mai multă varianță decât eroarea, testul F va fi semnificativ.

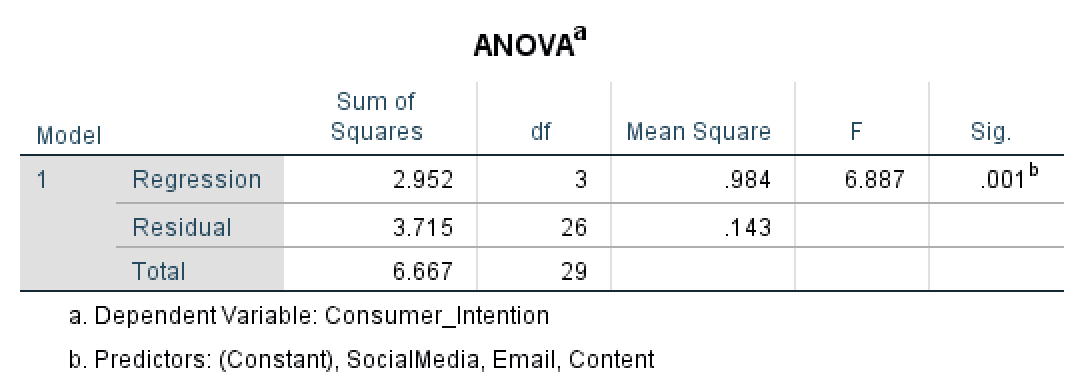
Tabel ANOVA SPSS arătând Sum of Squares, df, Mean Square, F și valorile Sig

Tabelul ANOVA afișează statisticile de potrivire a modelului de regresie

Să începem cu coloana Sum of Squares în ANOVA. Regression Sum of Squares (SSR) arată cantitatea de variație în variabila dependentă explicată de variabilele independente. În cazul nostru, modelul de regresie explică 2.952 unități de variație. Valori mai mari ale Regression SS indică că modelul explică mai multă varianță în rezultat - ceea ce este dezirabil.

Residual Sum of Squares (SSE) măsoară variația neexplicată sau eroarea în model. În cazul nostru, Residual Sum of Squares este 3.715. Valori reziduale mai mici sunt mai bune, deoarece indică mai puțină varianță neexplicată. Un rezidual de zero ar însemna predicție perfectă.

Total Sum of Squares este calculat prin adăugarea Regression Sum of Squares și Residual Sum of Squares, respectiv 6.667 în cazul nostru.

Următorul, să ne uităm la coloana Degree of Freedom (df) în ANOVA.

Regression df este egal cu numărul de variabile predictor din model (k). În cazul nostru, avem 3 predictori (Email, Content, SocialMedia), deci regression df = 3.

Residual df este calculat ca: n - k - 1, unde n este dimensiunea eșantionului, k este numărul de predictori, și 1 ține cont de interceptare. Cu 30 de eșantioane și 3 predictori:

30−3−1=2630 - 3 - 1 = 26

Total df este egal cu n - 1 (dimensiunea eșantionului minus unu), care este 29 în exemplul nostru.

Regression Mean Square este calculat prin împărțirea sumei pătratelor de regresie la gradul de libertate de regresie – în exemplul nostru 0.984. Residual Mean Square este calculat în același mod, prin împărțirea sumei pătratelor reziduale la gradul de libertate rezidual – respectiv, 0.143 în cazul nostru.

Coloana F în ANOVA reprezintă statisticile F care este probabil cantitatea cea mai importantă în testul ANOVA. Statisticile F egalează raportul dintre Regression Mean Square și Residual Mean Square și este folosit pentru a calcula valoarea P. În exemplul nostru, statisticile F sunt egale cu 6.887.

În final, coloana Sig. în ANOVA (valoarea P) ne spune dacă diferența dintre grupuri în modelul de regresie este semnificativă. Deoarece în cazul nostru P este 0.001, respectiv ≤ 0.05, diferența dintre grupurile Content, SocialMedia și Email este statistic semnificativă.

Coefficients

Ultimul tabel în output-ul regresiei este tabelul Coefficients. Aici putem găsi detalii despre Coeficientul Beta Nestandardizat și Eroarea Standard, Coeficientul Beta Standardizat, t și valoarea P pentru predictorii din modelul nostru.

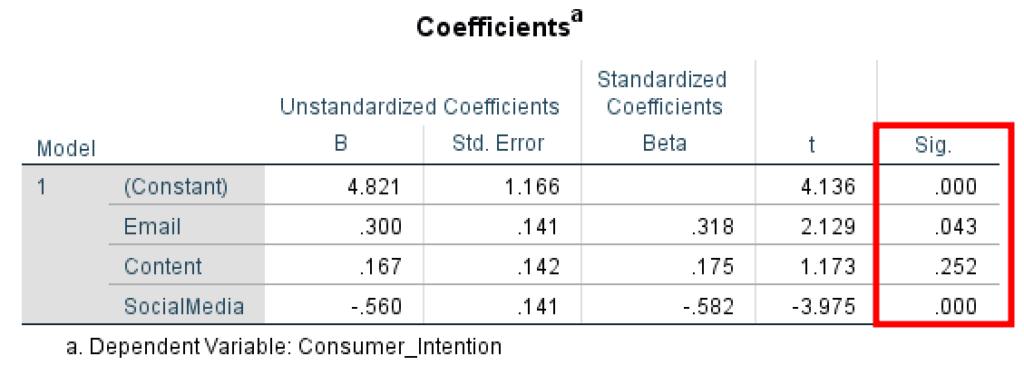
Tabel Coefficients SPSS arătând valorile Beta, Standard Error, statistici t și niveluri de semnificație pentru fiecare predictor

Tabelul Coefficients arată semnificația statistică a fiecărui predictor

Coeficientul Beta Nestandardizat măsoară variația în variabila rezultat pentru o unitate de schimbare în variabila predictor, unde valorile brute sunt afișate în scala originală.

Eroarea Standard a estimărilor măsoară distanța medie a punctelor de date observate de la linia de regresie. O valoare mare a erorii standard indică că mediile eșantionului sunt distribuite larg în jurul mediei populației. O valoare mică a erorii standard indică că media eșantionului și media populației sunt strâns corelate – un lucru bun.

Coeficienții Beta Standardizați (cunoscuți și ca ponderi beta) măsoară efectul fiecărui predictor când toate variabilele sunt standardizate să aibă o medie de 0 și deviație standard de 1. Aceasta îți permite să compari importanța relativă a predictorilor măsurați pe scale diferite. Un beta standardizat absolut mai mare indică un efect mai puternic.

Coloana de statistici t arată măsura deviației standard a coeficientului și este calculată prin împărțirea coeficientului Beta la eroarea sa standard. În general, o valoare mai mare de +2 sau -2 este considerată acceptabilă.

În final, coloana Sig. (valoarea P) în coeficienții de regresie arată semnificația statistică pentru fiecare predictor asupra variabilei rezultat, unde o valoare P ≤ 0.05 este considerată acceptabilă.

În exemplul nostru, putem observa că variabila predictor Email are un efect asupra variabilei rezultat Consumer_Intention (P = 0.043, < 0.05), prin urmare relația este statistic semnificativă.

Predictorul Content nu are efect asupra rezultatului Consumer_Intention (P = 0.252, > 0.05), prin urmare nu există semnificație statistică în modelul de regresie.

Predictorul SocialMedia are un efect asupra Consumer_Intention (P = 0.000, < 0.05), prin urmare relația dintre cele două variabile este statistic semnificativă.

În concluzie, cele mai importante valori pe care ar trebui să le verifici când cauți să interpretezi output-ul regresiei liniare multiple în SPSS sunt:

  • Rezultatele testului ANOVA one-way ne spun dacă diferența dintre grupuri în modelul de regresie este semnificativă la P ≤ 0.05.
  • Coeficientul de regresie arătând un efect semnificativ între predictor și variabila rezultat la P ≤ 0.05.

Exportă Output-ul Regresiei Liniare în SPSS

În final, să exportăm rezultatele regresiei liniare multiple folosind SPSS ca fișier .pdf pentru utilizare ulterioară. În fereastra Output a rezultatelor regresiei, dă click pe File → Export.

  • În fereastra Export Output, selectează opțiunea Portable Document Format (*.pdf). Alte opțiuni precum Word/RTF (.doc) și PowerPoint (.ppt) sunt disponibile în cazul în care preferi acele formate.
  • Tastează un File Name și Browse pentru locația în care preferi să salvezi rezultatele regresiei liniare multiple în SPSS.
  • Dă click pe butonul OK pentru a exporta output-ul SPSS.

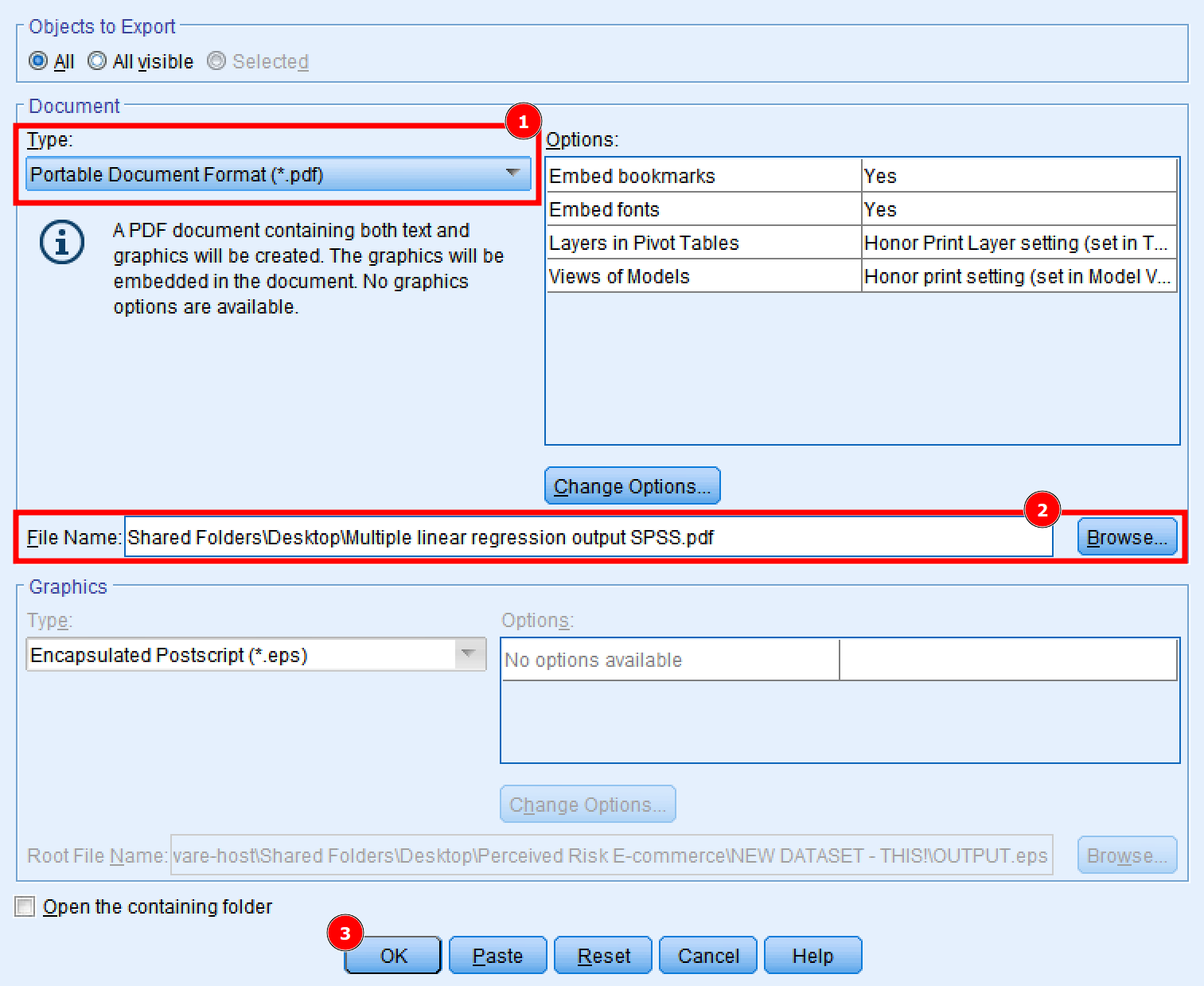
Dialog SPSS Export Output arătând selecția formatului PDF și opțiuni de locație fișier

Exportă output-ul regresiei în format PDF, Word sau PowerPoint

Fișierul conținând output-ul regresiei liniare multiple în SPSS este acum disponibil pentru utilizarea ta ulterioară.

Asumpțiile Regresiei Liniare Multiple

Înainte de a-ți interpreta rezultatele, este crucial să verifici că datele tale îndeplinesc asumpțiile regresiei liniare multiple. Încălcarea acestor asumpții poate duce la rezultate inexacte sau înșelătoare.

1. Linearitate

Relația dintre fiecare variabilă independentă și variabila dependentă ar trebui să fie liniară. Poți verifica acest lucru creând diagrame de dispersie pentru fiecare predictor împotriva variabilei rezultat.

Cum să testezi în SPSS: Creează diagrame de dispersie (Graphs → Legacy Dialogs → Scatter/Dot) pentru fiecare pereche predictor-rezultat. Caută un model liniar mai degrabă decât relații curbe.

2. Independența Observațiilor

Observațiile ar trebui să fie independente una de alta. Această asumpție este încălcată în cazuri precum măsurători repetate, date de serii temporale sau date grupate.

Cum să asiguri: Verifică designul tău de cercetare. Dacă ai măsurători repetate sau date grupate, vei avea nevoie de tehnici mai avansate precum modele mixte sau ecuații de estimare generalizate.

3. Homoscedasticitate

Varianța reziduurilor ar trebui să fie constantă pe toate nivelurile variabilelor independente. Cu alte cuvinte, răspândirea reziduurilor ar trebui să fie aproximativ egală pe linia de regresie. Învață mai multe despre ce înseamnă homoscedasticitatea în statistică.

Cum să testezi în SPSS: În dialogul Linear Regression, dă click pe Plots → adaugă ZPRED la axa X și ZRESID la axa Y. Diagrama de dispersie rezultată ar trebui să arate puncte dispersate aleator fără model de con sau evantai.

4. Normalitatea Reziduurilor

Reziduurile (erorile) ar trebui să fie aproximativ distribuite normal. Acest lucru este în special important pentru dimensiuni mai mici ale eșantionului.

Cum să testezi în SPSS: În dialogul Linear Regression, dă click pe Plots → bifează "Histogram" și "Normal probability plot". Histograma ar trebui să semene cu o curbă în formă de clopot, iar punctele pe graficul P-P ar trebui să cadă aproape de linia diagonală.

5. Lipsa Multicoliniarității

Variabilele independente nu ar trebui să fie prea strâns corelate una cu alta. Multicoliniaritatea ridicată umflă erorile standard și face dificilă evaluarea efectului individual al fiecărui predictor.

Cum să testezi în SPSS: În dialogul Linear Regression, dă click pe Statistics → bifează "Collinearity diagnostics". Uită-te la valorile VIF (Variance Inflation Factor). Valorile VIF peste 10 indică multicoliniaritate problematică. Valorile de toleranță sub 0.1 sugerează de asemenea probleme.

6. Lipsa Valorilor Extreme sau Cazurilor Influente Semnificative

Valorile extreme pot afecta disproporționat linia de regresie și duce la rezultate înșelătoare.

Cum să testezi în SPSS: În dialogul Linear Regression, dă click pe Save → bifează "Cook's distance" și "Standardized residuals". Valorile Cook's distance peste 1 sugerează cazuri influente. Reziduuri standardizate dincolo de ±3 indică potențiale valori extreme.

Întrebări Frecvente

Pentru a rula regresia multiplă în SPSS: (1) Mergi la Analyze → Regression → Linear, (2) Mută variabila ta dependentă în caseta 'Dependent', (3) Mută toate variabilele tale independente (predictori) în caseta 'Independent(s)', (4) Asigură-te că metoda este setată pe 'Enter', (5) Dă click pe OK. SPSS va genera tabele de output inclusiv Model Summary, ANOVA și Coefficients.
Concentrează-te pe aceste elemente cheie: (1) Verifică R² în Model Summary pentru a vedea procentul de varianță explicat, (2) Uită-te la valoarea Sig. în tabelul ANOVA - dacă P ≤ 0.05, modelul tău este semnificativ, (3) Examinează tabelul Coefficients pentru a vedea care predictori individuali sunt semnificativi (P ≤ 0.05), (4) Compară valorile Beta Standardizate pentru a determina care predictori au cel mai puternic efect.
Regresia liniară simplă analizează relația dintre O variabilă independentă și o variabilă dependentă, în timp ce regresia liniară multiplă examinează relația dintre DOUĂ SAU MAI MULTE variabile independente și o variabilă dependentă. Regresia multiplă îți permite să controlezi pentru variabile confundante și să evaluezi contribuția unică a fiecărui predictor.
Nu există o valoare 'bună' universală de R² - depinde de domeniul tău. În științele sociale, R² de 0.25-0.40 (25-40% varianță explicată) este adesea acceptabil. În științele fizice, ai putea aștepta R² peste 0.70. Concentrează-te pe dacă R² tău este statistic semnificativ și dacă modelul tău adaugă valoare predictivă semnificativă peste cunoștințele existente.
Tehnic nelimitat, dar practic constrâns de dimensiunea eșantionului. O regulă generală comună este să ai cel puțin 10-20 de observații pe variabilă predictor. De exemplu, cu 100 de participanți, nu ar trebui să folosești mai mult de 5-10 predictori. Prea mulți predictori relativ la dimensiunea eșantionului duce la supraadaptare și rezultate nesigure.
Statisticile F testează dacă modelul tău de regresie în ansamblu este statistic semnificativ. Compară varianța explicată de modelul tău împotriva varianței neexplicate. Un test F semnificativ (P ≤ 0.05) înseamnă că cel puțin una dintre variabilele tale predictor prezice în mod semnificativ rezultatul. Dacă F nu este semnificativ, niciunul dintre predictorii tăi nu adaugă predicție semnificativă.
În dialogul Linear Regression, dă click pe Statistics → bifează 'Collinearity diagnostics'. SPSS va afișa valorile VIF (Variance Inflation Factor) și Tolerance în tabelul Coefficients. Valorile VIF peste 10 sau Tolerance sub 0.1 indică multicoliniaritate problematică. Dacă este găsită, consideră eliminarea predictorilor strâns corelați sau combinarea lor în variabile compozite.

Concluzie

Sper că până acum ai obținut o înțelegere a modului de a calcula regresia liniară multiplă folosind SPSS, precum și cum să interpretezi output-ul regresiei liniare multiple în SPSS. După cum poți vedea, nu este atât de dificil.

Dacă aceasta este prima dată când efectuezi o regresie liniară în SPSS, îți recomand să repeți procesul de câteva ori și să încerci să folosești propriul tău set de date pentru analiza regresiei liniare multiple.

Dacă ești interesat să înveți mai multe despre tehnicile avansate de regresie, citește ghidurile noastre despre analiza de mediere în SPSS și analiza de moderare în SPSS.