Tutorial de regresie liniară SPSS care acoperă cum să rulezi, să calculezi și să interpretezi analiza de regresie în SPSS. Acest ghid demonstrează cum să calculezi o regresie liniară în SPSS folosind instrucțiuni pas cu pas cu un set de date exemplu.
Vei învăța cum să rulezi regresia liniară în SPSS, să interpretezi output-ul ecuației de regresie SPSS și să înțelegi statistici cheie inclusiv R Square, ANOVA și coeficienți. Acest tutorial se concentrează pe analiza regresiei liniare simple SPSS - tehnica fundamentală de analiză de regresie SPSS pentru examinarea relațiilor dintre două variabile.
Ce este Analiza de Regresie Liniară
Regresia liniară este o metodă statistică fundamentală pentru examinarea relației dintre variabile. Folosește o linie de regresie (numită și linia celor mai mici pătrate) pentru a modela cum una sau mai multe variabile independente (predictori) influențează o variabilă dependentă (rezultat).
Regresia liniară este una dintre cele mai utilizate tehnici de modelare predictivă în cercetare și analiza datelor, făcând-o esențială pentru studenți, cercetători și oameni de știință de date.
După cum implică numele, regresia liniară folosește o linie (numită și linia de regresie) pentru a măsura relația dintre una sau mai multe variabile. Gândește-te la această relație ca la cauză (variabila independentă) și efect (variabila dependentă) unde regresia liniară generează o linie pentru a arăta rezultatul.
În statistică, variabila independentă este adesea numită predictor sau variabilă explicativă. Variabila dependentă este uneori denumită variabilă prezisă sau rezultat.
Există două tipuri de regresie liniară:
- Regresia liniară simplă folosește O variabilă independentă pentru a prezice un rezultat
- Regresia liniară multiplă folosește două sau mai multe variabile independente
Acest tutorial se concentrează pe analiza regresiei liniare simple. În cercetare, relația de predicție este formulată prin intermediul unei ipoteze - de exemplu, investigarea impactului publicității asupra veniturilor.
Importă Date în SPSS
Deoarece acesta este un tutorial practic despre calcularea unei analize de regresie liniară în SPSS, vom avea nevoie de câteva date pentru a genera o linie de regresie.
Descarcă setul de date exemplu de mai jos pentru a urmări acest tutorial.
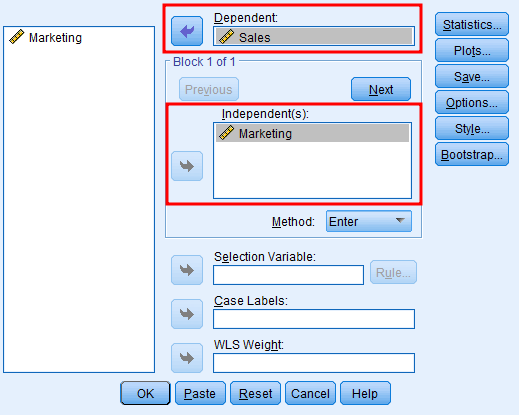
Să presupunem că vrem să investigăm efectul Publicității asupra Vânzărilor pentru o anumită companie. Iată cum arată setul de date Excel exemplu pe care l-ai descărcat mai sus.
Presupunând că ai descărcat setul de date Excel de mai sus, deschide SPSS Statistics, și în meniul superior, navighează la File → Import Data → Excel.
Navighează la locația fișierului Excel exemplu, selectează-l și dă click pe Open. Dă click pe OK când ești solicitat să citești fișierul Excel. Odată ce setul de date este importat în SPSS, ar trebui să arate astfel:
Acum, să aflăm cum să calculăm o regresie liniară în SPSS. În meniul superior SPSS navighează la Analyze → Regression → Linear.
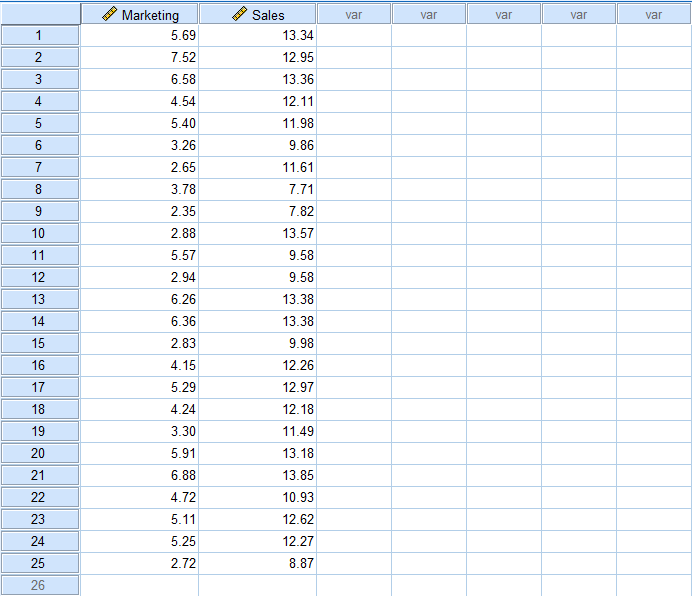
Accesarea regresiei liniare în SPSS prin Analyze → Regression → Linear
Următorul pas, trebuie să instruim SPSS care este variabila noastră dependentă și independentă în setul de date.
Reține, în regresia liniară, investigăm o relație cauzală între o variabilă independentă și o variabilă dependentă. În exemplul nostru Excel, variabila independentă este Marketing (cauză) și variabila dependentă este Sales (efect). Cu alte cuvinte, vrem să prezicem dacă variabila Sales este afectată de orice schimbări în variabila Marketing.
În fereastra Linear Regression, selectează variabila Sales și dă click pe butonul săgeată lângă caseta Dependent pentru a adăuga Sales ca variabilă dependentă în analiza de regresie.
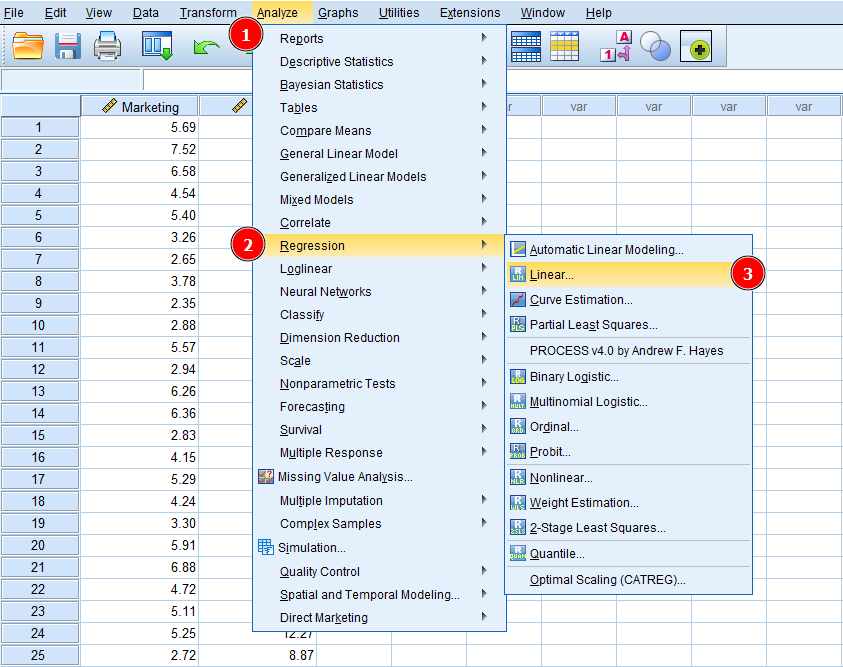
Adăugarea variabilei dependente (Sales) în regresia liniară SPSS
Fă același lucru pentru variabila Marketing, dar de această dată dă click pe săgeata lângă caseta Independent. Fereastra ta de analiză de regresie ar trebui să arate astfel:
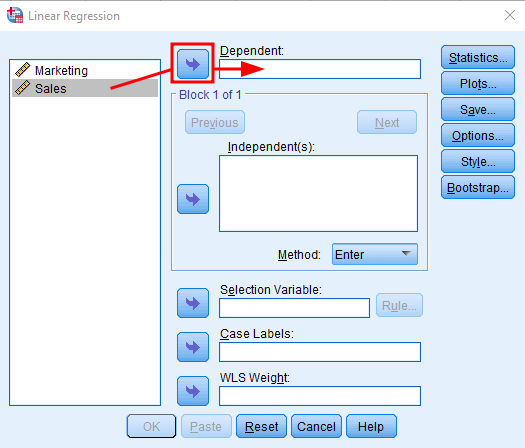
Adăugarea variabilei independente (Marketing) în regresia liniară SPSS
Putem folosi alte opțiuni de input pentru a personaliza analiza de regresie liniară în continuare, de exemplu, Method, Statistics, Plots, Style, etc. Pentru moment, vom păstra lucrurile simple și vom alege setările implicite deoarece sunt suficiente pentru acest caz.
Dă click pe OK pentru a porni analiza. Și iată cum arată rezultatele analizei de regresie liniară în SPSS:
Output complet al regresiei liniare SPSS cu toate statisticile cheie
Output-ul arată variabilele independente și dependente folosite în această analiză, Model Summary, ANOVA, Coefficients și statistici asociate. Să înțelegem ce ne spun rezultatele analizei de regresie.
Înțelegerea Rezultatelor Analizei de Regresie Liniară
Această secțiune explică semnificația fiecărui termen și valoare în output-ul SPSS, concentrându-se pe cele mai importante aspecte pentru analiza ta de cercetare.
-
Tabelul Variables Entered/Removed arată un rezumat descriptiv al analizei de regresie liniară.
-
Model 1 (Enter) înseamnă pur și simplu că toate variabilele solicitate au fost introduse într-un singur pas și li se acordă importanță egală. Modelul Enter este utilizat în mod obișnuit în analiza de regresie, motiv pentru care Model 1 este modelul de regresie implicit în SPSS.
-
Variables Entered arată variabila independentă (Marketing) folosită în această analiză. Nu au fost eliminate variabile, prin urmare coloana Variables Removed este goală.
-
În SPSS, variabila dependentă, în cazul nostru Sales, este specificată sub tabelul descriptiv.
-
Tabelul Model Summary ne spune un rezumat al rezultatelor analizei de regresie în SPSS.

Tabelul Model Summary SPSS din output-ul regresiei liniare
- R se referă la corelația variabilelor. Corelația este importantă pentru analiza de regresie deoarece putem presupune că o variabilă afectează alta dacă ambele variabile sunt corelate. Dacă două variabile nu sunt corelate, este probabil inutil să căutăm o relație de cauză și efect.
Corelația nu garantează o relație de cauză și efect, dar este o condiție necesară pentru ca o relație cauzală să existe.
Valoarea R variază de la -1 la +1, unde -1 este o corelație negativă perfectă, +1 este o corelație pozitivă perfectă și 0 reprezintă nicio corelație liniară între variabile.
În cazul nostru, R = 0.663 arată că variabilele Marketing și Sales sunt corelate.
-
R Square măsoară influența totală a variabilelor independente asupra variabilei dependente. Reține că valoarea R Square este explicată în procente (%). De exemplu, în exemplul nostru, R Square = 0.440 ceea ce înseamnă că 44% din Vânzări sunt influențate de strategia de Marketing a companiei.
-
Adjusted R Square este o penalizare aplicată în cazul în care modelul tău este non-parsimonios (nu este simplu sau eficient). Cu alte cuvinte simple, dacă cadrul tău conceptual de cercetare conține variabile care sunt inutile pentru a prezice un rezultat, va exista o penalizare pentru aceasta exprimată în valoarea Adjusted R Square.
În exemplul nostru, diferența dintre Adjusted R Square (0.416) și R Square (0.440) este 0.024, ceea ce este nesemnificativ.
Reține, ar trebui să căutăm explicații simple și nu complicate pentru fenomenul aflat sub investigație.
- Standard Error of the Estimate se referă la cât de precisă este predicția în jurul liniei de regresie. Dacă valoarea ta de Standard Error este între -2 și +2, atunci linia de regresie este considerată a fi mai aproape de valoarea adevărată.
În cazul nostru, Standard Error of the Estimate = 1.40, ceea ce este un lucru bun.
- Testul ANOVA este un precursor al analizei de regresie liniară. Cu alte cuvinte, ne spune dacă rezultatele regresiei liniare pe care le-am obținut folosind eșantionul nostru pot fi generalizate la populația pe care o reprezintă eșantionul.
Reține că pentru ca o analiză de regresie liniară să fie validă, rezultatul ANOVA ar trebui să fie semnificativ (p < 0.05). În plus, modelele de regresie ar trebui să îndeplinească asumpții cheie inclusiv homoscedasticitatea (varianță constantă), linearitatea și normalitatea reziduurilor.

Tabelul ANOVA SPSS din output-ul regresiei liniare
- Sum of Squares măsoară cât de mult punctele de date din setul tău deviază de la linia de regresie și te ajută să înțelegi cât de bine un model de regresie reprezintă datele modelate.
Regula empirică atât pentru Regression cât și pentru Residual Sum of Squares este că cu cât valoarea este mai mică, cu atât mai bine datele reprezintă modelul tău.
Reține că Sum of Squares va fi întotdeauna un număr pozitiv, cu 0 fiind cea mai mică valoare și reprezentând cea mai bună potrivire a modelului.
- DF în ANOVA înseamnă Degree of Freedom (Grad de Libertate). Cu cuvinte simple, DF arată numărul de valori independente care au fost folosite pentru a calcula estimarea.
Reține că o dimensiune mai mică a eșantionului înseamnă de obicei un grad mai mic de libertate (cum este exemplul nostru). În contrast, o dimensiune mai mare a eșantionului permite un grad mai mare de libertate, care poate fi util în respingerea unei ipoteze nule false și în obținerea unui rezultat semnificativ.
-
Mean Square în ANOVA este folosit pentru a determina semnificația tratamentelor (factori, respectiv variația dintre mediile eșantionului). Mean Square este important în calcularea raportului F.
-
Testul F în ANOVA este folosit pentru a găsi dacă mediile dintre două populații sunt semnificativ diferite. Valoarea F calculată din date (F=18.071) este de obicei denumită statistici F și este utilă când se caută respingerea unei ipoteze nule.
-
Sig. înseamnă Semnificație. Dacă nu vrei să intri în detaliile testului ANOVA, aceasta este probabil coloana din rezultatul ANOVA pe care ai dori să o verifici mai întâi. O valoare Sig. < 0.05 este considerată semnificativă. În exemplul nostru, Sig. = 0.000 care este mai mic de 0.05, prin urmare, semnificativ.
În final, suntem gata să trecem la tabelul rezultatelor analizei de regresie în SPSS.
- În tabelul Coefficients, doar o valoare este esențială pentru interpretare: valoarea Sig., respectiv ultima coloană - deci să începem cu ea mai întâi.

Tabelul Coefficients SPSS din output-ul regresiei liniare
- Sig. cunoscută și ca valoarea p arată nivelul de semnificație pe care variabila independentă îl are asupra variabilei dependente. Similar cu ANOVA, dacă valoarea Sig. este < 0.05, există o semnificație între variabilele din regresia liniară.
În cazul nostru, Sig. = 0.000 arată o semnificație puternică între variabila independentă (Marketing) și variabila dependentă (Sales).
- Unstandardized B (Beta) reprezintă practic panta liniei de regresie între variabilele independente și dependente și ne spune pentru o creștere cu o unitate în variabila independentă, cu cât va crește variabila dependentă.
În cazul nostru, pentru fiecare creștere cu o unitate în Marketing, Sales va crește cu 0.808. Creșterea unității poate fi exprimată în, de exemplu, monedă.
Rândul Constant din tabelul Coefficients arată valoarea variabilei dependente când variabila independentă = 0.
- Coefficients Std. Error este similar cu deviația standard pentru o medie.
Cu cât valoarea Standard Error este mai mare, cu atât punctele de date pe linia de regresie sunt mai răspândite. Cu cât punctele de date sunt mai răspândite, cu atât mai puțin probabil va fi găsită semnificație între variabile.
- Valoarea Standardized Coefficients Beta variază de la -1 la +1, cu 0 însemnând nicio relație; 0 la -1 însemnând relație negativă și 0 la +1 relație pozitivă. Cu cât valoarea Standardized Coefficient Beta este mai aproape de -1 sau +1, cu atât relația dintre variabile este mai puternică.
În cazul nostru, Standardized Coefficient Beta = 0.663 arată o relație pozitivă între variabila independentă (Marketing) și variabila dependentă (Sales).
- t reprezintă testul t și este folosit pentru a calcula valoarea p (Sig.). În termeni mai largi, testul t este folosit pentru a compara valoarea medie a două seturi de date și pentru a determina dacă provin din aceeași populație.
Întrebări Frecvente
Concluzie
După cum poți vedea, a învăța cum să calculezi o regresie liniară în SPSS nu este dificil. Pe de altă parte, înțelegerea output-ului regresiei liniare poate fi un pic provocatoare, în special dacă nu știi care valori sunt relevante pentru analiza ta.
Cel mai important lucru de reținut când evaluezi rezultatul analizei tale de regresie liniară este să cauți semnificație statistică (Sig. < 0.05).
Pentru tehnici avansate de regresie, explorează analiza de moderare în SPSS pentru a testa efectele de interacțiune între variabile și analiza de mediere în SPSS pentru a înțelege mecanismele prin care variabilele își exercită efectele.